Dynamic induction control for mitigation of wake-induced power losses: a wind tunnel study under different inflow conditions

Dynamic induction control (DIC), also known as the pulse method, is a wake mixing strategy that has shown promising results for mitigating wake-induced power losses in wind farms. It relies on dynamic collective blade pitching to enhance turbulent mixing, thereby accelerating the wake recovery. Experimental validation of this concept has been primarily limited to single-turbine cases under idealised conditions without shear and negligible turbulence. This paper presents a wind tunnel study to investigate the wake recovery improvement induced by DIC in single- and two-turbine configurations, as well as the potential power gains in a virtual three-turbine configuration. The study includes experiments under baseline uniform inflow and two realistic atmospheric boundary layer inflows. Short-range continuous-wave lidar measurements are used to remotely map the time-averaged wake characteristics of each turbine in vertical cross-sections at various downstream positions. First, the wake recovery of the upstream turbine is analysed as a function of pitch amplitude and frequency, with the latter expressed by the dimensionless Strouhal number. Next, the cascading effect of upstream turbine actuation on the wake of a downstream turbine in greedy mode is examined. Finally, wind farm power gains are assessed in a virtual three-turbine configuration. Compared to the baseline greedy case, improved wake recovery is observed at both the upstream and downstream turbines, solely through upstream turbine actuation across all cases. This improvement is attributed to the formation of large-scale coherent structures, which excite shear layer instabilities and accelerate the onset of wake recovery. The effect is particularly pronounced at higher pitch amplitude, while differences across Strouhal number remain minor, suggesting stronger control authority through increased pitch amplitude. Despite a decrease in DIC-added wake recovery with increasing inflow turbulence, potential power gains for the wind farm persist. Overall, this study demonstrates consistent benefits and adaptability of DIC under realistic inflow conditions, highlighting its greater potential in low-turbulence environments.

1 Introduction

Wake-induced power losses and fatigue loads pose a persistent challenge for wind turbines in wind farms, with power losses exceeding 40 % under full-wake overlap conditions (Barthelmie et al., 2009). This arises from the energy extraction process, which exposes downstream turbines to a wind field with reduced momentum and increased turbulence (Porté-Agel et al., 2020). Since technical and economic constraints make wake effects largely unavoidable, advanced wind farm flow control strategies are being developed to mitigate wake losses and ultimately reduce the levelised cost of energy (Meyers et al., 2022). These strategies often involve turbine-level actuation (e.g. yaw or pitch) based on optimal control setpoints to improve inflow conditions for downstream turbines (Houck, 2022). When effectively implemented, this can benefit overall plant performance through increased power production or reduced fatigue loads. Although first commercial solutions are emerging, widespread adoption remains limited, requiring further research and development.

Typically, wind farm flow control implementation focuses foremost on wind farm power maximisation (van Wingerden et al., 2020). To this end, research has primarily centred on wake steering and static induction control strategies (Kheirabadi and Nagamune, 2019). Wake steering involves intentionally yawing upstream turbines to deflect their wakes away from downstream turbines, thereby increasing the total power output (Fleming et al., 2015; Hulsman et al., 2024). This concept has received the most attention and development, but challenges remain due to the strong dependence of optimal setpoints on temporal variations in wind direction (Dallas et al., 2024) and power loss behaviour (Howland et al., 2020; Hulsman et al., 2022a). On the other hand, static induction control involves derating upstream turbines through pitch control, torque control, or a combination of both to reduce their wake deficit and increase the energy available to downstream turbines (Houck, 2022). Inconsistent simulation results have undermined interest in this concept. However, power gains may still be achievable under partial wake conditions or with closely spaced turbines (van der Hoek et al., 2019; Zúñiga Inestroza et al., 2024).

Wake mixing strategies based on individual or collective pitching have demonstrated potential for increased wind farm power production (Meyers et al., 2022). Unlike wake steering and static induction control, these techniques aim to actively excite wake instabilities, promoting enhanced turbulent mixing and accelerating wake recovery (Houck, 2022). The collective-pitch-based approach, commonly termed dynamic induction control (DIC) or the pulse method, is the focus of this study and its literature review. First results from large-eddy simulation (LES) studies report power gains of up to 16 % (Goit and Meyers, 2015) and 7 % (Goit et al., 2016) in a 10×5 wind farm without and with entrance effects, respectively. However, these studies used a computationally expensive optimisation approach that yielded impractical control signals. Building on this, Munters and Meyers (2018) introduced a simplified method based on sinusoidal thrust variations to mimic the periodic shedding of vortex rings. This approach provided power gains of up to 5 % in a 4×4 wind farm, decreasing to approximately 2 % at higher inflow turbulence. Yılmaz et al. (2018) further advanced this by synthesising a periodic signal based on optimal generator torque and pitch control, achieving power gains of up to 25 % in a two-turbine configuration under uniform inflow in LES. These gains diminished or even disappeared with increasing turbulence intensity and integral length scale.

Unfortunately, experimental validation of DIC is currently limited to a few wind tunnel studies. Frederik et al. (2020b) report power gains of up to 4 % in a three-turbine configuration under two different atmospheric boundary layer (ABL) inflows. Combining wind tunnel experiments with numerical simulations, Wang et al. (2020) indicate maximum power gains of 3.6 % in a three-turbine array with 5 % inflow turbulence intensity. Based on particle image velocimetry measurements, van der Hoek et al. (2022) demonstrate improved wake recovery due to DIC applied to a single turbine under uniform inflow. Although no power gains were achieved in a virtual two-turbine configuration, subsequent results with a second physical turbine showed a gain of 0.6 % (van der Hoek et al., 2024).

While initial numerical and experimental investigations into DIC show promising results, several knowledge gaps remain open regarding the performance of DIC parameters under different inflow and operating conditions, including the level of wake recovery improvement, achievable wind farm power gains, cascading effects on downstream turbines, the physical mechanisms behind DIC and ABL flow interactions, and the impact on fatigue loads, among others. Further validation through wind tunnel experiments is essential to bridge the gap between numerical simulations and currently absent field tests, offering well-controlled and repeatable conditions. This paper presents a wind tunnel study to investigate the wake recovery improvement and wind farm power gains induced by DIC under baseline uniform inflow and two realistic ABL inflows. Specifically, the following aspects are addressed:

1. exploring the wake recovery improvement as a function of pitch amplitude and frequency;

2. examining the cascading effect of upstream turbine actuation on a downstream turbine and its wake;

3. evaluating the potential wind farm power gains in a virtual three-turbine configuration.

The remainder of the paper is structured as follows: Sect. 2 outlines the experimental methodology, Sect. 3 presents the results, Sect. 4 discusses the experimental findings, and Sect. 5 provides the concluding remarks of the study.

2 Methodology

This section outlines the experimental methodology. Section 2.1 introduces the wind tunnel facility and the active grid used to generate ABL inflows. Section 2.2 describes the model wind turbine, while Sect. 2.3 explains the greedy and DIC operating modes. Section 2.4 details the flow measurement techniques, including a short-range continuous-wave lidar and complementary hot-wire measurements. Finally, Sect. 2.5 provides an overview of the experimental setup and measurement procedure.

2.1 Wind tunnel facility

The experiments are carried out in the large wind tunnel at ForWind, University of Oldenburg, Germany. It is a Göttingen-type wind tunnel with a contraction ratio of 4:1, a cross-section of 3 m × 3 m, and a closed test section length of 30 m. It consists of five 6 m long movable segments, allowing operation in open, partially open, or closed test section configuration. The airflow is driven by four 110 kW fans capable of reaching wind speeds of up to 42 m s⁻¹ with turbulence intensity levels below 0.2 % when no active grid is installed. A cooling system is used to maintain a constant temperature during operation, while the roof of each test section segment is adjusted to achieve a zero pressure gradient. An active grid can be installed at the wind tunnel nozzle to generate tailored, reproducible turbulent, and sheared inflows. The active grid consists of 80 shafts with square flaps, which can be independently controlled to modify the local blockage of the flow. This is achieved by dynamically varying the angle of the flaps according to user-defined motion protocols (Kröger et al., 2018; Neuhaus et al., 2021).

2.2 Model wind turbine

Two in-house developed MoWiTO 0.6 model wind turbines are used during the measurement campaign. The rotor blades are designed according to the NREL-5 MW reference turbine (Jonkman et al., 2009), with a geometric scaling factor of 1:217, resulting in a rotor diameter of 0.58 m and a blockage ratio below 3 % in the wind tunnel. To account for scaling effects and manufacturing constraints, the blades feature an SD7003 low-Reynolds-number (Re) airfoil with increased chord length and tailored twist distribution along the span (Schottler et al., 2016). While this improves aerodynamic performance in the operating low-Re regimes typical of wind tunnel testing, the power coefficient (C_P) remains unavoidably lower than that of full-scale turbines (Wang et al., 2021). The nacelle houses a direct current (DC) motor (Faulhaber 3863H048CR) acting as a generator and a stepper motor (Faulhaber AM2224-R3-4.8-36) used for collective blade pitching, both equipped with an encoder. The DC motor's encoder measures the rotational speed (rpm), while the aerodynamic torque is estimated from the voltage drop across a shunt resistor. The stepper motor's encoder measures the collective blade pitch angle. These values are then used to calculate the electrical power generated by the model wind turbine. Additionally, a field-effect transistor acts as a variable resistor within the circuit, enabling control of the generator torque for rotor speed adjustment. Furthermore, the tower base is instrumented with strain gauges (HBM 1-DY43-3/350) in full Wheatstone bridge configuration to obtain thrust measurements. Calibration is done by hanging known weights on the nacelle's rear through a pulley system at the start of the measuring campaign. All control algorithms (e.g. torque control, pitch control) are executed in real time on a National Instruments cRIO-9066 system, while acquiring the data at 5 kHz.

2.3 Control strategies

Two different control modes are implemented during the experiments: (i) baseline greedy control and (ii) DIC.

2.3.1 Greedy mode

The greedy control mode follows the conventional Kω² control law by Bossanyi (2000), which aims to maximise the turbine's power output in the partial-load region. This is achieved by setting the generator torque (Q_G) proportional to the square of the rotor speed (ω), as follows:

$$\begin{array}{}\text{(1)}& Q_{\mathrm{G}}=K{\mathit{\omega }}^{\mathrm{2}}={\displaystyle \frac{\mathit{\rho }\mathit{\pi }{R}^{\mathrm{5}}{C}_{\mathrm{Q}}({\mathit{\lambda }}^{*},{\mathit{\beta }}^{*})}{\mathrm{2}{\mathit{\lambda }}^{{*}^{\mathrm{2}}}}}{\mathit{\omega }}^{\mathrm{2}},\end{array}$$

where K is the controller gain, depending on the air density (ρ), rotor radius (R), torque coefficient (C_Q), and design tip speed ratio (λ^*). C_Q is a function of both λ^* and the optimal pitch angle (β^*). The generator torque is adjusted via a proportional-integral-derivative (PID) controlled external voltage, which ensures the rotor speed is maintained at the point of optimal efficiency. MoWiTO 0.6 uses a setpoint function Q_G(ω) derived from characterisation experiments conducted at various wind speeds and pitch angles at the start of each measurement campaign. For this campaign, the turbines operated optimally at a tip speed ratio λ=5.60, thrust coefficient C_T=0.86, and power coefficient C_P=0.37, at an inflow wind speed of 7 m s⁻¹.

2.3.2 DIC mode

The DIC mode applies a sinusoidal signal to the collective blade pitch controller to induce periodic thrust oscillations, while the baseline generator torque controller remains active to maintain operation near optimal aerodynamic efficiency. Although pitch actuation causes fluctuations and a reduced mean in C_Q, the controller gain K is not updated during the experiments. The control signal to the stepper motor is parameterised by the pitch excitation amplitude (A) and frequency (f_β), with the latter typically expressed in terms of the dimensionless Strouhal number (St). Here, St represents the ratio of the flow oscillation speed due to periodic pitching to the convective flow speed, defined as

$$\begin{array}{}\text{(2)}& St={\displaystyle \frac{f_{\mathit{\beta }}D}{u_{\mathrm{\infty }}}},\end{array}$$

where D is the rotor diameter and u_∞ is the average inflow wind speed at hub height. The dynamic collective blade pitching ($\widehat{\mathit{\beta }}$) is then described by

$$\begin{array}{}\text{(3)}& \widehat{\mathit{\beta }}={\mathit{\beta }}_{\mathrm{0}}+A\sin \left(\mathrm{2}\mathit{\pi }{\displaystyle \frac{St{u}_{\mathrm{\infty }}}{D}}t\right),\end{array}$$

where β₀ is the fine pitch angle that maximises power in the partial-load region and t is the time. The range of St for this study is chosen based on previous numerical (Munters and Meyers, 2018; Yılmaz et al., 2018) and experimental studies (Frederik et al., 2020b; Wang et al., 2020), which report optimal wake recovery within St ∈ [0.24,0.38]. Figure 1a illustrates the collective blade pitch signal under both greedy and DIC modes. The DIC signal is implemented at u_∞ = 7 m s⁻¹, with A=2° and St=0.30 (i.e. f_β=3.63 Hz). This corresponds to a low-frequency actuation of about 0.017 kHz at the NREL-5 MW scale, with one cycle completed every 59 s. Figure 1b depicts the C_T for both control modes, with the DIC case showing a clear harmonic response to the sinusoidal pitch actuation.

Figure 1 Time series excerpt depicting (a) the collective blade pitch signal and (b) the thrust coefficient under greedy and DIC ($St=\mathrm{0.30},A=\mathrm{2}\mathit{°}$) operation modes.

2.4 Flow measurements

2.4.1 WindScanner lidar

Wake measurements are performed with a short-range continuous-wave WindScanner lidar, developed and manufactured by the Technical University of Denmark (DTU). This remote sensing device provides highly spatially resolved flow measurements over large measurement planes in a flexible manner, without flow disturbance. Its effectiveness has been demonstrated in previous wind tunnel experiments combined with model wind turbines (e.g. van Dooren et al., 2017; Hulsman et al., 2020, 2022b; Zúñiga Inestroza et al., 2024), showing good agreement with hot-wire measurements to capture the main trends of the average streamwise velocity field and dissipation rate of turbulence in wind turbine wakes. It is equipped with a steerable scan head, driven by two prism motors and a focus motor, enabling precise focus point adjustments. This allows for measurements in both staring and scanning modes, following user-defined trajectories. The WindScanner uses a coherent detection method to determine the Doppler frequency shift in the backscattered signal of a focused laser beam within a probe volume. At the start of each measurement campaign, the focus point is calibrated by determining the lidar's location and orientation relative to the experimental setup using a Leica total station. Additionally, an infrared detector card is used to verify the commanded measurement points. Further details on the use and setup of WindScanners in wind tunnel experiments can be found in van Dooren et al. (2017) and Hulsman et al. (2022b).

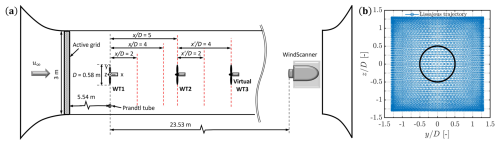
Figure 2 (a) Top-view schematic of the experimental setup (not to scale), detailing the arrangement of the model wind turbines and the wake measurement positions (red dashed lines). (b) Lissajous scanning trajectory used by the WindScanner to map the wake in vertical cross-sections at each downstream location.

In this study, a single WindScanner is used to retrieve the local streamwise velocity component (u) of the wind velocity vector at a sampling rate of 451.7 Hz. This approach neglects the lateral (v) and vertical (w) components, potentially introducing relative errors of up to 2.4 % (cf. uncertainty analysis of single-Doppler reconstruction in Appendix A1). Taking this into account, u can be derived according to

$$\begin{array}{}\text{(4)}& \begin{array}{rl}u=& {\displaystyle \frac{\mathrm{1}}{\cos \mathit{\varphi }\cos \mathit{\theta }}}\left(v_{\mathrm{LOS}}-v\sin \mathit{\varphi }\cos \mathit{\theta }-w\sin \mathit{\theta }\right)\\ \approx & {\displaystyle \frac{v_{\mathrm{LOS}}}{\cos \mathit{\varphi }\cos \mathit{\theta }}},\end{array}\end{array}$$

where v_LOS is the measured line-of-sight wind speed along the laser's beam direction, and ϕ and θ are the azimuth and elevation angles of the line-of-sight direction, respectively.

During the measurement campaign, the WindScanner is used to obtain time-averaged wake characteristics in vertical cross-sections at downstream distances $x/D\in \mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5},\mathrm{7},\mathrm{9}\mathit{\}}$. The coordinate system is defined at the rotor centre of the first turbine, where x, y, and z are the longitudinal, transversal, and vertical directions, respectively. Figure 2a provides a schematic of the experimental setup (described in Sect. 2.5), with red dashed lines indicating the wake measurement positions. Each vertical scan follows a Lissajous scanning trajectory comprising of 5000 points (Fig. 2b), with a period of 15 s per scan. The scanning process is repeated for 10 min per case, resulting in over 40 scans per vertical plane at every downstream distance. Postprocessing of the data includes interpolation and averaging onto a grid with 0.13 D by 0.13 D cells. This yields approximately 300 data points at the central grid cell at hub height and considerably higher measurement density near the boundaries of the scanning area, consistent with the Lissajous trajectory.

2.4.2 Hot-wire array

An important limitation when using WindScanner measurements in a wind tunnel is the probe-volume averaging effect, which limits the accuracy of turbulence estimates. Since the laser focuses on a thin cylindrical volume rather than an infinitesimal point, turbulent structures with a length scale smaller than the probe-volume length are partially filtered out (Uluocak et al., 2024). Therefore, complementary hot-wire measurements are conducted for a limited number of cases under uniform inflow, providing insights into the turbulence development in the wake of a DIC actuated turbine compared to the greedy case. The array consists of 19 one-dimensional hot wires mounted on an aluminium structure in a horizontal line at hub height, spanning over a range of $y/D\in [-\mathrm{1.25},\mathrm{1.25}]$. A traverse system facilitates the measurement of horizontal wake profiles at $x/D\in \mathit{\{}\mathrm{2},\mathrm{3},\mathrm{5}\mathit{\}}$. Two Dantec Dynamics 54N80 multi-channel Constant Temperature Anemometry (CTA) systems are used to sample data at 6 kHz over a period of 120 s. Calibration is done before and after the measurements against a Prandtl tube positioned approximately 2 m in front of the traversing structure.

2.5 Experimental setup and measurement procedure

The experimental setup involved a wind tunnel configuration with a partially open test section, comprising four connected segments with a total length of 24 m. The last segment was removed to accommodate the WindScanner, installed on a steel platform near the diffuser, alongside a PALAS AGF 10.0 seeding generator to provide adequate aerosol circulation for laser backscattering. The inflow wind speed was monitored with a Prandtl tube positioned perpendicular to the upstream turbine's rotor plane at hub height, 0.9 m to the left of the tunnel centreline.

The measurement campaign included experiments in both single- and two-turbine configurations. Figure 3a shows a downstream view of the two-turbine configuration, while Fig. 3b highlights the installation of the WindScanner. In the single-turbine configuration, the first turbine (WT1) was positioned 9.55 D (5.54 m) from the nozzle on the tunnel centreline. This configuration aimed to investigate the dependence of wake recovery on pitch amplitude and Strouhal number. Specifically, the time-averaged wake response of WT1 was examined with the WindScanner at downstream positions $x/D\in \mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5}\mathit{\}}$, under both greedy and DIC operation modes. For the DIC cases, pitch frequencies corresponding to St ∈ $\mathit{\{}\mathrm{0.25},\mathrm{0.30},\mathrm{0.40}\mathit{\}}$ and amplitudes A ∈ {1°,2°} were considered.

In the two-turbine configuration, a second turbine (WT2) was installed 5 D (2.9 m) downstream of WT1. Here, the focus was on the cascading effect of WT1 actuation on WT2. To this end, the wake of WT2 was examined in response to WT1 operating in greedy and DIC modes, while WT2 remained in greedy mode throughout. For each case, the wake of WT2 was mapped with the WindScanner at downstream positions $x^{\prime }/D$ ∈ {2,4}, with $x^{\prime }/D=\mathrm{0}$ defined relative to the position of WT2.

Figure 3 (a) Downstream view of the experimental setup with two MoWiTO 0.6 turbines and the WindScanner (yellow square). (b) Close-up of the WindScanner lidar used to remotely map the wake.

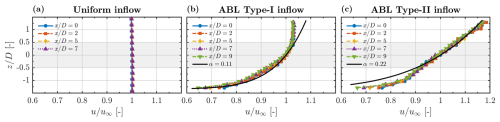
Figure 4 Vertical profiles of normalised wind speed ($u/u_{\mathrm{\infty }}$) measured by the WindScanner along the empty wind tunnel test section for different inflow conditions. The grey shaded region represents the rotor area.

All experiments were conducted in the partial-load region at $u_{\mathrm{\infty }}=(\mathrm{7.0}\pm \mathrm{0.1})$ m s⁻¹, resulting in a rotor-based Reynolds number of $Re\approx \mathrm{2.9}\times {\mathrm{10}}^{\mathrm{5}}$. Although lower than that of full-scale turbines, typically 𝒪(10⁶) to 𝒪(10⁷), Chamorro et al. (2012) suggest Re independence of the main wake statistics for rotor-based $Re>\mathrm{9.3}\times {\mathrm{10}}^{\mathrm{4}}$. The campaign encompassed three different inflow conditions: (i) uniform (no shear), (ii) ABL Type I (α=0.11), and (iii) ABL Type II (α=0.22), where α represents the best-fit power-law exponent accounting for wind shear across the rotor area. The active grid was installed at the nozzle and used in active mode to generate the ABL inflows, while no grid (empty nozzle) was used for the uniform inflow. The WindScanner was used to characterise the inflow development along the empty test section at $x/D\in \mathit{\{}\mathrm{0},\mathrm{2},\mathrm{5},\mathrm{7},\mathrm{9}\mathit{\}}$. The vertical profiles of normalised wind speed ($u/u_{\mathrm{\infty }}$) for all three inflow conditions are shown in Fig. 4. Note that $x/D=\mathrm{9}$ is excluded for the uniform inflow case due to a faulty data set. Each point represent the spatially averaged streamwise velocity component across all horizontal positions ($y/D$) at each height ($z/D$). Despite slight variations for the ABL cases, the wind speed distribution remained fairly stable along the test section for all inflow cases. The inflow turbulence intensity (TI) was measured along the tunnel centreline at hub height using the WindScanner's staring mode for both ABL cases, while hot-wire measurements were used for the uniform inflow case. Note that the measured TI using the WindScanner is inherently low-pass filtered due to probe-volume averaging effects, as explained in Sect. 2.4.2. Table 1 summarises the TI values for all inflows at $x/D\in \mathit{\{}\mathrm{0},\mathrm{2},\mathrm{5},\mathrm{7},\mathrm{9}\mathit{\}}$. The stability of the flow throughout the measurement domain is corroborated under uniform inflow, with an average TI of 0.2 %. For ABL Type I, TI shows slight downstream variations, while for ABL Type II, it decays as expected for fully developed flows behind a grid. Given the reproducibility of the inflows generated by the active grid, all experiments are expected to have experienced similar TI variations without compromising the validity of the results.

Table 1 Development of turbulence intensity (TI) along the wind tunnel test section at hub height for different inflow conditions, measured using hot wires (HW) or WindScanner staring mode (WS).

3 Results

The experimental results are organised into three main sections. Section 3.1 focuses on the single-turbine configuration, analysing the impact of WT1 actuation on wake recovery improvement, wake turbulence development, and thrust coefficient behaviour. Section 3.2 centres on the two-turbine configuration, exploring the cascading effect of WT1 actuation on WT2's wake recovery and thrust coefficient. Section 3.3 evaluates the potential wind farm power gains in a virtual three-turbine configuration.

3.1 Single-turbine configuration: impact of pitch actuation amplitude and Strouhal number

3.1.1 Wake recovery of WT1

The impact of WT1 pitch actuation with DIC on wake recovery is analysed in terms of pitch amplitude and Strouhal number relative to the greedy case across different inflow conditions. To illustrate this, Fig. 5 presents wake contours of the normalised streamwise velocity difference between DIC and the baseline greedy case $(u_{\mathrm{DIC}}-u_{\mathrm{Greedy}})/u_{\mathrm{\infty }}$. Each row corresponds to a distinct inflow type, with each subfigure depicting a different downstream position, $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5}\mathit{\}}$. Two pitch amplitudes, A ∈ {1°,2°}, are examined under uniform inflow (Fig. 5a–f), while only A=2° is considered under both ABL inflows (Fig. 5g–l), as it yielded stronger wake recovery under baseline uniform inflow. Also, since similar trends are observed for different Strouhal numbers (cf. wind speed deficit profiles of WT1 at hub height in Appendix B1), only results from WT1 actuation at St=0.30 are displayed.

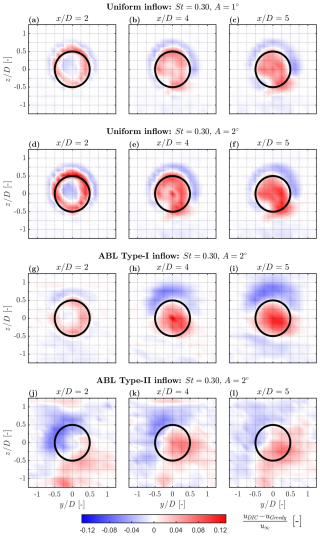
Figure 5 Time-averaged wake contours of WT1 depicting the normalised streamwise velocity difference between operation under DIC mode at St=0.30 and the baseline greedy mode $(u_{\mathrm{DIC}}-u_{\mathrm{Greedy}})/u_{\mathrm{\infty }}$. Each row represents a different inflow condition at downstream locations $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5}\mathit{\}}$. The black circumference outlines the edges of a virtual downstream turbine. The counter-rotating wake is shown from the WindScanner perspective, looking upstream towards WT1, thus perceived as a clockwise rotation.

In general, at $x/D=\mathrm{2}$, DIC induces a wind speed deficit (blue regions) at the wake centre and the surrounding flow, while increasing the wind speed in an annulus near the rotor edges (red regions). This corresponds to an accelerated transition from a double- to a single-Gaussian wake profile. Further downstream, at $x/D$ ∈ {4,5}, the annulus gradually expands to encompass almost the entire swept area of a virtual turbine (indicated by the black circumference), with the magnitude of increased wind speed also rising, especially for DIC cases with higher amplitude (A=2°). Additionally, the wind speed deficit in the surrounding flow becomes more pronounced, concentrating in a semiannular-shaped region above hub height, indicating predominant momentum entrainment from aloft. These patterns are consistent under both uniform and ABL Type I inflow conditions, although the wind speed deficit patches are slightly more pronounced for the ABL case. This can be attributed to the enhanced vertical momentum entrainment triggered by DIC (Brown et al., 2025), which represents a dominant mechanism for energy replenishment in the wake of turbines interacting with boundary layer inflows (Cal et al., 2010).

Comparatively, under ABL Type II inflow, the wake re-energisation induced by WT1 actuation exhibits a markedly asymmetric distribution. Specifically, at $x/D=\mathrm{2}$, the wind speed deficit is concentrated in the second quadrant, while patches of increased wind speed appear in the third and fourth. Quadrants are defined anticlockwise from the positive x axis, following standard mathematical convention. This asymmetry may be linked to the development of nacelle- and tower-induced turbulence, which is enhanced by DIC (van der Hoek et al., 2022). Since wake TI below hub height is typically reduced under strongly sheared ABL inflow (Porté-Agel et al., 2020), their relative contribution may explain the observed pattern. Further downstream, at $x/D\in \mathit{\{}\mathrm{4},\mathrm{5}\mathit{\}}$, the wind speed deficit diffuses more into the surrounding flow compared to previous cases, while regions of higher wind speed spread across the rotor area, remaining predominantly deflected to the right. This asymmetric behaviour can be partly attributed to the effect of wake rotation under sheared inflow conditions, which causes high-momentum flow from aloft to be transported downward and low-momentum near the ground upward (Gebraad et al., 2016). Consequently, the wake of a turbine operating in greedy mode deflects slightly to the right when viewed upstream (Fleming et al., 2014). This effect is particularly pronounced under highly sheared and turbulent inflow but appears to be disrupted by DIC. In fact, analysis of the wake centre revealed reduced lateral deflection across all DIC cases under ABL inflow. This finding aligns with Brown et al. (2025), who similarly observed that DIC reduces wake skew under sheared and veered inflow conditions.

To quantify the wake recovery improvement from WT1 actuation, Fig. 6 presents bar charts of the normalised rotor equivalent wind speed ($u_{\mathrm{REWS}}/u_{\mathrm{\infty }}$) for WT1 operating under greedy and DIC modes, assuming a full-wake overlap scenario. Each subchart corresponds to a different inflow condition, with groups of four bars comparing the two modes at downstream positions $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5}\mathit{\}}$. The u_REWS method provides a weighted average wind speed across the rotor swept area, accounting for spatial variations in the velocity field (Wagner et al., 2011). In this study, the rotor area is segmented into five ring segments based on the measured wake cross-sections, as follows:

$$\begin{array}{}\text{(5)}& u_{\mathrm{REWS}}=\sqrt[\mathrm{3}]{\sum _{i=\mathrm{1}}^{\mathrm{5}}{u}_i^{\mathrm{3}}{\displaystyle \frac{A_i}{A_{\mathrm{R}}}}},\end{array}$$

where u_i is the average wind speed within the ith ring segment, A_i is the area of the ith ring segment, and A_R is the rotor swept area. Since the outer rings cover a larger area, they are weighted more heavily and contribute more to the energy that would be captured by a virtual downstream turbine, neglecting tip losses. Percentage values indicate the relative change in $u_{\mathrm{REWS}}/u_{\mathrm{\infty }}$ with respect to the baseline greedy case. Red arrows highlight the optimal recovery, while the grey error bars indicate the rotor average uncertainty of $u_{\mathrm{REWS}}/u_{\mathrm{\infty }}$, calculated according to the standard uncertainty propagation method used in van Dooren et al. (2017) and Hulsman et al. (2022b).

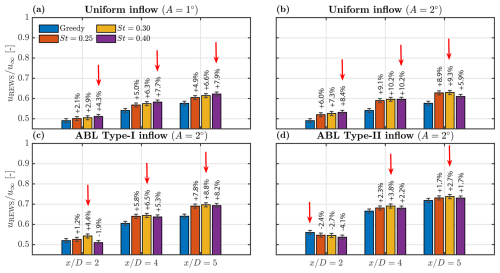
Figure 6 Wake recovery of WT1 expressed by the normalised rotor equivalent wind speed ($u_{\mathrm{REWS}}/u_{\mathrm{\infty }}$). Each subchart corresponds to a different inflow condition, with groups of four bars comparing results from WT1 operating in greedy and DIC modes at downstream positions $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5}\mathit{\}}$. Percentage values indicate the relative change with respect to the baseline greedy case. Red arrows highlight the optimal recovery.

Experiments under uniform inflow reveal a dependence of wake recovery on pitch amplitude and Strouhal number. For A=1°, the optimal wake recovery relative to the greedy case occurs at the highest frequency tested (St=0.40) across all downstream positions, reaching a peak of 7.9 % at $x/D=\mathrm{5}$. In comparison, for A=2°, the optimal St varies with downstream distance: St=0.40 at $x/D=\mathrm{2}$, a similar recovery for $St\in \mathit{\{}\mathrm{0.30},\mathrm{0.40}\mathit{\}}$ at $x/D=\mathrm{4}$, and St=0.30 at $x/D=\mathrm{5}$. The highest recovery (10.2 %) is achieved at $x/D=\mathrm{4}$. Noteworthy is that the magnitude of wake recovery improvement is more responsive to increased amplitude than to changes in Strouhal number. For ABL Type I inflow, the optimal recovery consistently aligns with St=0.30 at all downstream distances, with a maximum improvement of 8.8 % at $x/D=\mathrm{5}$. For ABL Type II inflow, the optimal recovery is also achieved with St=0.30, reaching a peak of 3.8 % at $x/D=\mathrm{4}$, while no benefit is attained at $x/D=\mathrm{2}$ due to the asymmetry described earlier.

Figure 7 Downstream evolution of local turbulence intensity (TI) profiles in the wake of WT1 at hub height under uniform inflow conditions. Each subfigure compares the baseline greedy case with different DIC cases at downstream locations $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{3},\mathrm{5}\mathit{\}}$. Shaded grey regions indicate the rotor swept area.

3.1.2 Turbulence development in the wake of WT1

To better understand the improved wake recovery observed when DIC mode is active, the turbulence development in the wake of WT1 is analysed under uniform inflow conditions for selected DIC cases in comparison to the greedy case. As a first metric, Fig. 7 presents horizontal wake profiles of the local turbulence intensity (TI) at hub height for downstream distances $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{3},\mathrm{5}\mathit{\}}$. These profiles provide indication on the level of wind speed fluctuations within the wake, computed with the local time series from hot-wire measurements as follows:

$$\begin{array}{}\text{(6)}& \mathrm{TI}\left(y\right)={\displaystyle \frac{\mathit{\sigma }\left(y\right)}{\langle u\left(y\right)\rangle }},\end{array}$$

where σ(y) is the local standard deviation and 〈u(y)〉 is the local mean wind speed, both as functions of the transversal position y. Remarkably, compared to the greedy mode, all DIC cases exhibit a significant increase in local turbulence and an earlier transition to the far-wake region. The latter is distinguished by the merging of the TI profile into a single peak at the wake centre, resulting from shear layer expansion following the breakdown of tip vortices, which otherwise inhibit momentum exchange with the surrounding flow (Lignarolo et al., 2015; Porté-Agel et al., 2020). Once this occurs, the far wake is said to be reached, which gradually transitions into fully developed decaying turbulence (i.e. homogeneous isotropic turbulence) before eventually recovering to undisturbed conditions (Neunaber et al., 2020). Moreover, when looking at the effect of increasing Strouhal number St ∈ {0.25,0.30} with the same amplitude A=2°, the resulting differences in local TI are marginal. Conversely, increasing the amplitude from A=1° to A=2° while keeping the same St=0.30 leads to a more pronounced increase in TI, while also exhibiting an earlier transition to the far wake. This is evidenced by the local maximum around $x/D=\mathrm{3}$ at the wake centre for A=2°. Further downstream, at $x/D=\mathrm{5}$, TI is already decaying for the DIC cases, whereas for the greedy case, the merging has not yet occurred and instead the local TI is still building up.

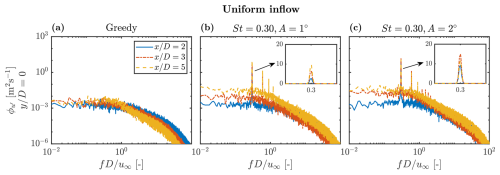
Figure 8 Downstream evolution of the local power spectra of wind speed fluctuations (${\mathit{\varphi }}_{u^{\prime }}$) at the wake centreline ($y/D=\mathrm{0}$) of WT1 under uniform inflow conditions. For DIC cases, zoomed insets illustrate the downstream development of the dominant coherent structure at St=0.30.

As a second metric, Fig. 8 compares the downstream evolution of the local power spectra ${\mathit{\varphi }}_{u^{\prime }}$ along the wake centreline $y/D=\mathrm{0}$ for the greedy case and two DIC cases with the same St=0.30 but different amplitude. This provides insight into the wake energy distribution across different turbulence scales, as well as the presence of coherent structures. The power spectra are computed with the standard Welch algorithm in MATLAB (2024), using the local time series of the wind speed fluctuations, $u^{\prime }\left(y\right)=u\left(y\right)-\langle u\left(y\right)\rangle$. The frequency axis is expressed in terms of the dimensionless Strouhal number. In general, the energy content remains largely unchanged across all downstream locations for the baseline greedy case, consistent with the slow turbulence build-up observed in the local TI profiles. On the other hand, the DIC cases exhibit not only higher energy spectra but also distinct peaks at the frequency of pitch actuation St=0.30 and its higher harmonics. This indicates the presence of large-scale coherent structures, which can be associated with the emergence of vortex rings, as reported in Munters and Meyers (2018) and Yılmaz et al. (2018). In fact, Yılmaz et al. (2018) show that these structures cause an earlier wake breakdown, enhancing the momentum entrainment into the wake core. Furthermore, looking at the spectra of different amplitude cases, the convergence to a single spectrum with similar energy across all frequencies by $x/D=\mathrm{3}$ indicates an earlier transition to the far-wake region for the high-amplitude case (A=2°). The zoomed-in view of the dominant peak at St=0.30 confirms that a turbulence plateau is reached at $x/D=\mathrm{3}$, followed by a decay at $x/D=\mathrm{5}$. In contrast, the low-amplitude case (A=1°) exhibits a slower turbulence build-up, with the highest energy content observed at $x/D=\mathrm{5}$. Additionally, although not shown here, spectral analysis of the shear layer region at the rotor edges reveals an even more rapid turbulence development for both amplitude cases. This is reasonable since the transition to the far-wake region starts with the breakdown of the helical tip-vortex system into small-scale turbulence structures (Lignarolo et al., 2015) but also results in the formation of vortex rings due to periodic flow disturbances induced by DIC. This fuels momentum transport towards the wake core in response to a faster shear layer expansion.

Figure 9 Time series excerpts comparing WT1's thrust coefficient (C_T,WT1) under greedy and DIC (St=0.30) operation modes across different inflow conditions.

3.1.3 Thrust coefficient of WT1

To qualitatively illustrate the periodic thrust oscillations (C_T,WT1) induced by WT1 pitch actuation, Fig. 9 presents time series excerpts of WT1 operating in greedy and DIC (St=0.30) modes across different inflow conditions. For each case, the time series are synchronised to analyse the turbine behaviour when exposed to identical inflow conditions. Additionally, the raw signals are low-pass filtered at 12 Hz to remove high-frequency noise and facilitate visualisation. To prevent phase distortion, a sixth-order Butterworth filter is applied using the filtfilt function in MATLAB (2024). C_T,WT1 is then calculated as follows:

$$\begin{array}{}\text{(7)}& C_{\mathrm{T},\mathrm{WT}\mathrm{1}}={\displaystyle \frac{F_{\mathrm{T},\mathrm{WT}\mathrm{1}}}{\mathrm{0.5}\mathit{\rho }\mathit{\pi }{R}^{\mathrm{2}}{u}_{\mathrm{\infty }}^{\mathrm{2}}}},\end{array}$$

where F_T,WT1 is the instantaneous thrust force measured via strain gauges at the tower base of WT1, ρ is the average air density, R is the rotor radius, and u_∞ is a 10 min averaged wind speed measured by the Prandtl tube at hub height. Note that for cases under ABL inflow conditions, this point measurement does not fully represent inflow variations across the rotor area. Nevertheless, it is observed that DIC effectively induces periodic C_T,WT1 oscillations across all inflow conditions. To quantify these variations, Table 2 summarises statistical trends in the mean and standard deviation of C_T,WT1 across all cases. The reported values represent 10 min averages, obtained after low-pass filtering the data at 250 Hz. This choice filters out high-frequency noise while preserving most relevant dynamic components. Further increases in the cut-off frequency resulted in negligible variations.

Table 2 Statistical trends in the mean and standard deviation (in parentheses) of C_T,WT1 under greedy and DIC operating modes across different inflow conditions.

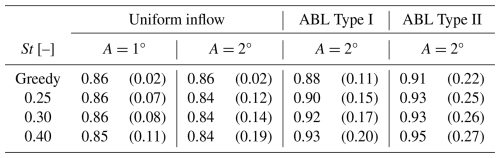
Under uniform inflow, the mean C_T,WT1 remains nearly constant across St cases at low pitch amplitude (A=1°), while a slight decrease occurs at higher amplitude (A=2°). By comparison, DIC markedly increases the standard deviation of C_T,WT1 across all actuated cases. Given the negligible inflow TI, the relative increase over the greedy case peaks at 450 % for A=1° and 850 % for A=2°, both at St=0.40. Moreover, at low amplitude, optimal recovery aligns with St=0.40, corresponding to the highest fluctuation energy in C_T,WT1. In contrast, at higher amplitude, optimal recovery initially aligns with St=0.40 earlier downstream but shifts to St=0.30 further downstream, despite this not corresponding to the highest standard deviation (see Fig. 6). Comparatively, experiments under ABL inflow show a moderately higher mean C_T,WT1 even in the baseline greedy case, particularly for the strongly sheared ABL Type II. This is attributed to the vertical shear, which shifts the wind centre of pressure (i.e. the point where the resultant wind force acts) above hub height due to higher momentum in the upper half of the rotor. Also, since DIC induces periodic thrust oscillations, its interaction with sheared inflow likely causes a shift in the thrust load centre. This leads to an increase in mean C_T,WT1 with increasing St, being most pronounced at St=0.40 due to more energetic fluctuations, as reflected by the higher standard deviation. Nevertheless, it is worth noting that optimal recovery aligns with St=0.30 under both ABL inflows (Fig. 6), despite this not corresponding to the highest fluctuation energy in C_T,WT1. Furthermore, the sheared and turbulent nature of ABL inflows yields a higher baseline standard deviation, thereby reducing the relative increase in DIC-induced fluctuations up to 82 % for ABL Type I and 23 % for ABL Type II. Overall, these observations indicate that optimal St depends not only on the magnitude of induced thrust fluctuations but also on the interaction between actuation amplitude, inflow turbulence, and wake evolution.

3.2 Two-turbine configuration: cascading effect of upstream turbine actuation on a downstream turbine

3.2.1 Wake recovery of WT2

To illustrate the cascading effect of WT1 pitch actuation on WT2's wake recovery, Fig. 10 presents wake contours of the normalised streamwise velocity difference $(u_{\mathrm{DIC}}-u_{\mathrm{Greedy}})/u_{\mathrm{\infty }}$ resulting from WT1 operating in DIC and greedy modes, while WT2 remains in greedy mode. Each row corresponds to a distinct inflow condition, with each subfigure depicting a different downstream location $x^{\prime }/D$ ∈ {2,4}. Since similar cascading trends are observed across all St cases (cf. wind speed deficit profiles of WT2 at hub height in Appendix B2), only results from WT1 actuation at St=0.30 are displayed.

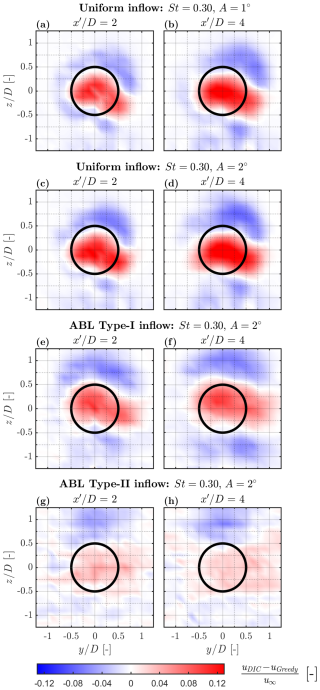
Figure 10 Time-averaged wake contours of WT2 depicting the normalised streamwise velocity difference $(u_{\mathrm{DIC}}-u_{\mathrm{Greedy}})/u_{\mathrm{\infty }}$ resulting from WT1 operating in DIC and greedy modes, while WT2 remains in greedy mode. Each row corresponds to a different inflow condition at downstream locations $x^{\prime }/D\in \mathit{\{}\mathrm{2},\mathrm{4}\mathit{\}}$, with $x^{\prime }/D=\mathrm{0}$ defined relative to the position of WT2. The black circumference outlines the edges of a virtual downstream turbine. The counter-rotating wake is visualised from the WindScanner perspective, looking upstream towards WT2, thus perceived as a clockwise rotation.

In general, WT1 actuation consistently enhances WT2's wake recovery across all inflow conditions. Notably, the wake contours exhibit patches of increased wind speed (red regions) spanning nearly the entire rotor area of a virtual downstream turbine, concurrently surrounded by wind speed deficit patches (blue regions) above and below. A slight extension of the high-speed region towards the right-hand side, beyond the rotor area, is also observed, likely due to wake rotation effects. These patterns indicate enhanced turbulent entrainment in WT2's wake as a result of WT1 actuation, which not only improves recovery of its own wake but also induces thrust oscillations at WT2, as described in Sect. 3.2.2. The cascading effects are present across all St cases, becoming slightly more pronounced at higher amplitude (A=2°). Furthermore, under ABL inflow, the overall patterns persist but appear more diffuse for ABL Type II. This is due to the impact of higher ambient turbulence and a concurrent reduction in cascading fluctuations at WT2.

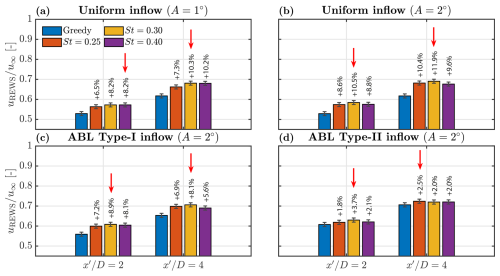
Figure 11 Wake recovery of WT2 expressed by the normalised rotor equivalent wind speed ($u_{\mathrm{REWS}}/u_{\mathrm{\infty }}$) at downstream positions $x^{\prime }/D$ ∈ {2,4}, with $x^{\prime }/D=\mathrm{0}$ defined relative to the position of WT2. Each subchart corresponds to a different inflow condition, with groups of four bars comparing results from WT1 operating in greedy and DIC modes, while WT2 remains in greedy mode. Percentage values indicate the relative change with respect to the baseline greedy case. Red arrows highlight the optimal recovery.

To quantify the wake recovery improvement of WT2, Fig. 11 presents bar charts of the normalised rotor equivalent wind speed ($u_{\mathrm{REWS}}/u_{\mathrm{\infty }}$) at downstream distances $x^{\prime }/D$ ∈ {2,4}. Each subchart corresponds to a distinct inflow condition, with groups of four bars comparing results from WT1 operating in greedy and DIC modes, while WT2 remains in greedy mode. Under uniform inflow, the magnitude of wake recovery improves with increasing amplitude and downstream distance, reaching optimal gains with St=0.30 at $x^{\prime }/D=\mathrm{4}$. Specifically, a relative increase of 10.3 % for A=1° and 11.9 % for A=2° is observed. The alignment with St=0.30 for both amplitudes is attributed to the higher turbulence levels in WT2's wake, which promote faster wake recovery even without WT1 actuation. Interestingly, the improvement in WT2's wake recovery due to WT1 actuation is similar to, or even exceeds, that of WT1's wake. This is related to the higher turbulence in WT2's wake, as well as to the fact that the energy content of the induced thrust oscillations at WT2 remains comparable to that of the actuated WT1, as described in Sect. 3.2.2. Furthermore, similar trends are observed under ABL inflow, albeit with slightly smaller improvements, as the increased ambient turbulence reduces cascading fluctuations at WT2. For ABL Type I, the relative increase peaks at 8.9 % with St=0.30 at $x^{\prime }/D=\mathrm{2}$ and then decreases to 8.1 % at $x^{\prime }/D=\mathrm{4}$. For ABL Type II, the wake recovery improvement is further reduced, reaching a maximum of 3.7 % with St=0.30 at $x^{\prime }/D=\mathrm{2}$ and 2.5 % with St=0.25 at $x^{\prime }/D=\mathrm{4}$.

3.2.2 Thrust coefficient of WT2

In this section, the cascading effect of WT1 pitch actuation on WT2 is analysed in terms of induced thrust fluctuations. Figure 12 compares time series excerpts of WT2's thrust coefficient (C_T,WT2) resulting from WT1 operating in greedy and DIC (St = 0.30) modes across different inflow conditions, while WT2 remains in greedy mode. C_T,WT2 is calculated similarly to WT1, as follows:

$$\begin{array}{}\text{(8)}& C_{\mathrm{T},\mathrm{WT}\mathrm{2}}={\displaystyle \frac{F_{\mathrm{T},\mathrm{WT}\mathrm{2}}}{\mathrm{0.5}\mathit{\rho }\mathit{\pi }{R}^{\mathrm{2}}{u}_{\mathrm{\infty }}^{\mathrm{2}}}},\end{array}$$

where F_T,W2 is the instantaneous thrust force measured via strain gauges at the tower base of WT2. In general, C_T,WT2 exhibits clear periodic fluctuations in response to WT1's harmonic pitch actuation, which results in periodic excitation of the flow impinging on WT2. Notably, the induced C_T,WT2 fluctuations are less pronounced under ABL inflow conditions, particularly for ABL Type II, due to the dominant effect of increased ambient turbulence. Moreover, Table 3 summarises statistical trends in the mean and standard deviation of C_T,WT2. Since WT1 pitch actuation improves wake recovery, both the mean and standard deviation of C_T,WT2 increase across all DIC cases compared to the baseline greedy case. The cascading effect on thrust fluctuations is particularly evident in the standard deviation under uniform inflow, with a relative increase of up to 200 % for A=1° and 250 % for A=2°. Comparatively, under ABL inflow, the relative increase is reduced to 80 % for ABL Type I and 13 % for ABL Type II.

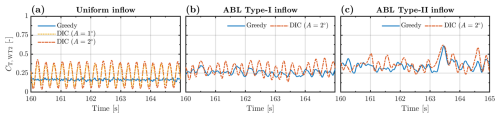
Figure 12 Time series excerpts of WT2's thrust coefficient (C_T,WT2) in response to WT1 operating in greedy or DIC mode under different inflow conditions, while WT2 remains in greedy mode throughout.

Table 3 Statistical trends in the mean and standard deviation (in parentheses) of C_T,WT2 in response to WT1 operating in greedy or DIC mode under different inflow conditions, while WT2 remains in greedy mode throughout.

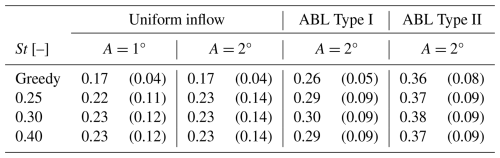
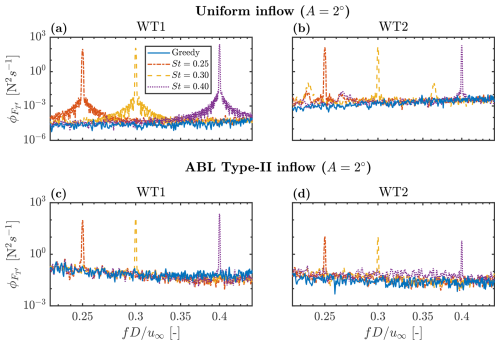
Figure 13 Power spectra of induced thrust fluctuations (${\mathit{\varphi }}_{F_{T^{\prime }}}$), zoomed into the St range corresponding to DIC pitch actuation frequencies. Only cases under uniform and ABL Type II inflow conditions are displayed to illustrate the cascading effect in response to WT1 operating in greedy or DIC mode, while WT2 remains in greedy mode throughout.

Furthermore, Fig. 13 compares the power spectra of induced thrust fluctuations (${\mathit{\varphi }}_{F_{T^{\prime }}}$) for both WT1 and WT2, zoomed into the St range corresponding to DIC pitch actuation frequencies. Cases under uniform inflow and ABL Type II are selected to illustrate the cascading behaviour in the spectra for DIC cases with A=2°. Under uniform inflow conditions, the DIC-induced peaks not only cascade to WT2 but also exhibit energy levels comparable to those observed at the actuated WT1. This is consistent for both amplitude cases, A ∈ {1°,2°}, explaining why the improvement in WT2's wake recovery is similar to or even exceeds that of WT1. Also, note that since WT2 operates within WT1's turbulent wake, its thrust fluctuation energy remains higher even when WT1 operates in greedy mode. In contrast, under ABL inflow conditions, the DIC-induced peaks still cascade to WT2 but with lower energy content compared to WT1, due to the dominant role of ambient turbulence, as noted earlier. This also explains the reduced improvement in WT2's wake recovery improvement under ABL conditions.

3.3 Virtual three-turbine configuration: wind farm power gains

This section evaluates the potential wind farm power gains resulting from WT1 operating in DIC mode relative to the baseline greedy mode. The analysis considers a virtual three-turbine configuration under fully waked conditions, with longitudinal spacings of 5 D between WT1 and WT2 and 4 D between WT2 and WT3. The first two turbines are physically installed in the tunnel, while WT3 is a virtual turbine based on WindScanner data, thereby constituting a real–real–virtual turbine configuration. The 4 D spacing for WT3 is set by the minimum focus distance of the WindScanner. WT3's virtual power is estimated from the u_REWS computed in Sect. 3.2.1, assuming greedy operation with the same optimal efficiency as WT1 (C_P=0.37), without accounting for Re effects. Accordingly, only WT1 alternates between greedy and DIC modes, while WT2 and WT3 remain in greedy mode throughout.

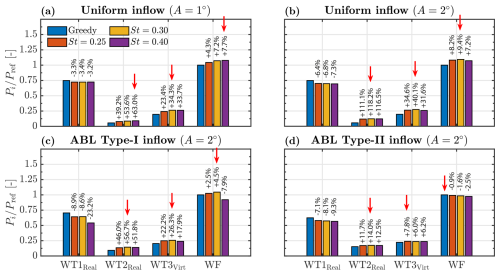
Figure 14 Wind farm power gain using a real–real–virtual turbine configuration. The power ratio ($P_i/P_{\mathrm{ref}}$) is shown for individual turbines (WT1, WT2, WT3) and the overall wind farm (WF), with WT1 operating in both greedy and DIC modes, while WT2 and virtual WT3 remain in greedy mode. Each subchart corresponds to a different inflow condition. Percentage values indicate the relative change with respect to the baseline greedy case, with P_ref representing the wind farm power with all turbines in greedy mode. Red arrows highlight the optimal gains.

Figure 14 displays the mean power ratio ($P_i/P_{\mathrm{ref}}$) for individual turbines (WT1, WT2, WT3) and the entire wind farm (WF), where P_i represents a 10 min average of the measured electrical power at WT1 and WT2, as well as the virtual power of WT3. $P_{\mathrm{ref}}={\sum }_{i=\mathrm{1}}^{\mathrm{3}}{P}_{i,\mathrm{Greedy}}$ is the total wind farm power output when all three turbines operate in greedy mode. Each subchart corresponds to a different inflow condition, with percentage values indicating the relative change for individual turbines and the whole wind farm with respect to the baseline greedy case. Red arrows highlight the optimal gains due to WT1 actuation.

In general, experiments under uniform inflow show that WT1 operating in DIC mode experiences higher power losses with increasing pitch amplitude, peaking at 3.4 % for A=1° and 7.3 % for A=2°, while losses remain similar across all St cases. For WT2, the highest power gains occur at St=0.40 for A=1° and St=0.30 for A=2°, with optimal gains nearly doubling as amplitude increases, reaching 63.0 % at A=1° and 118.2 % at A=2°. These trends align with the wake recovery improvement shown in Fig. 6. However, it is worth noting that the relative gains based on WT2's power measurements are higher than those estimated from virtual power using WindScanner data (cf. Appendix C1, where WT2's virtual power is computed in the same manner as for virtual WT3). This discrepancy arises from the C_P dependence on Re, which reduces aerodynamic efficiency at lower wind speeds. Consequently, the power gain at WT2 reflects both the effective increase in wind speed due to DIC and the increase in C_P. The latter is a drawback of wind tunnel testing, resulting in smaller wind farm power gains but without affecting the qualitative trends, as described in Appendix C. In contrast, power estimates at virtual WT3 inherently compensate for the C_P dependence on Re, as the virtual power is computed assuming a constant C_P across all cases. This assumption more closely resembles the behaviour of full-scale turbines but leads to higher power estimates for virtual WT3 compared to WT2 measurements. Nevertheless, the overall trends remain consistent regardless of the assumed C_P. Specifically, the power gain at WT3 peaks at St=0.30 for both amplitude cases, with slightly higher gains at higher amplitude, reaching 34.3 % at A=1° and 40.1 % at A=2°. Overall, the combined wind farm power gain reaches up to 7.7 % and 9.4 % for the A=1° and A=2° cases.

Under ABL inflow, the power loss at WT1 is generally comparable to that observed under uniform inflow conditions, except for the DIC case with St=0.40 under ABL Type I, which exhibits a substantially higher loss of 23.2 %. Power spectrum analysis of the torque signal revealed a significant increase in low-frequency energy content compared to other DIC cases, indicating that the loss was driven by large fluctuations in generator torque, which in turn caused significant power fluctuations. This is suspected to have been caused by a bug in the turbine's operating code introducing communication delays in the system after a long run-time. Nevertheless, consistent with trends in wake recovery improvement (Sect. 3.1.1 and 3.2.1), the relative power gain for WT2, virtual WT3, and the wind farm aligns with St=0.30 for ABL Type I, peaking at 56.7 %, 26.3 %, and 4.5 %, respectively. Also in agreement with wake recovery trends, the relative power gain is reduced for ABL Type II, peaking at 14.0 % with St=0.30 for WT2 and 7.8 % with St=0.25 for WT3, with no net gain at the farm level.

4 Discussion

This study provides insights into the wake recovery improvement induced by DIC as a function of pitch amplitude and Strouhal number, along with its cascading effects on a downstream turbine operating in greedy mode and the resulting wind farm power gains under baseline uniform inflow and two realistic ABL inflows. To this end, wind tunnel experiments were conducted in single- and two-turbine configurations, incorporating an active grid to generate atmospheric-like inflows, WindScanner lidar measurements to remotely map the wakes of individual turbines, and an array of hot wires to analyse the wake turbulence development.

Compared to conventional wind tunnel techniques such as particle image velocimetry (PIV) and laser Doppler anemometry (LDA), WindScanner measurements enable flexible and efficient remote mapping of turbine wakes at multiple downstream locations with high spatial resolution. Depending on the experimental setup and WindScanner operation mode (staring or scanning), phase-averaged characteristics, turbulence dissipation rates, and spectral or time series data can be analysed, albeit constrained by the maximum temporal resolution of 451.7 Hz and the probe-volume averaging effect (Hulsman et al., 2022b; van Dooren et al., 2022). In this study, WindScanner measurements were used to obtain highly spatially resolved time-averaged wake characteristics at different downstream locations, while complementary hot-wire measurements gave insights into the local turbulence development in the wake of a DIC-actuated turbine.

First, results from the single-turbine configuration show that DIC actuation consistently enhances WT1's wake recovery across all tested combinations of pitch amplitude and Strouhal number. However, the level of DIC-added recovery responds more positively to increased forcing amplitude than to changes in St. This behaviour is attributed to the magnitude of induced thrust oscillations (C_T,WT1) and turbulence development in the wake. As shown in Fig. 7, increasing St at constant amplitude yields minor variations in local TI, whereas increasing amplitude at fixed St produces a marked rise in local TI, further accelerating the onset of wake recovery. More intricately, the optimal St depends not only on the level of induced thrust fluctuations (Sect. 3.1.3) but also on the spatial development of coherent structures (Fig. 8), which is in turn influenced by both the forcing amplitude and inflow turbulence. Furthermore, consistent with numerical studies (Munters and Meyers, 2018; Yılmaz et al., 2018), the wake recovery enhancement achieved by DIC decreases under strongly sheared and highly turbulent inflow conditions. This effect relates to the dominant role of high ambient turbulence, which inherently promotes natural wake mixing, thereby reducing the control authority achieved through DIC-induced C_T,WT1 fluctuations. Nonetheless, this study underscores the potential adaptability of DIC to realistic inflow conditions.

Second, results from the two-turbine configuration shed light on the cascading effect of WT1 actuation on a downstream turbine (WT2). Remarkably, despite remaining in greedy mode, WT2's wake recovery is consistently enhanced when WT1 operates in DIC mode. This enhancement is attributed to the dynamic coupling between WT1's wake and the periodic DIC perturbation at WT1's rotor plane, which induces a pulsating flow pattern at the pitch actuation frequency (Fig. 8). Consequently, WT2 exhibits periodic C_T,WT2 fluctuations with energy levels comparable to those at the DIC-actuated WT1 (Fig. 13), which are assumed to drive the enhanced recovery. As a result, WT2's wake recovery is similar to, or even exceeds, that of WT1 (Fig. 11). Interestingly, WT2's optimal recovery predominantly aligns with WT1 actuation at St=0.30 across all inflow conditions. Moreover, as in the single-turbine experiments, the cascading effects decrease with increasing inflow turbulence. Future work should further explore these cascading effects, particularly from a fundamental fluid dynamics perspective.

Third, the assessment of wind farm power gains in a virtual three-turbine configuration demonstrates consistent power benefits under uniform and ABL Type I inflows. The absence of net power gains at the farm level under ABL Type II is primarily due to the higher power losses experienced by the model wind turbine (approximately 10 %) compared to those expected in full-scale turbines. Supporting this, aeroelastic simulations using the NREL-5 MW reference turbine (D=126 m) show power losses below 1.6 % for all DIC cases under both uniform and ABL inflows (cf. Appendix D). These results are more closely aligned with reported losses from LES studies using actuator disc or actuator line models (e.g. Yılmaz et al., 2018; Frederik et al., 2020a; Coquelet et al., 2022). Moreover, the increased power losses are a limitation of the model wind turbine, whose power curve is more sensitive to pitch angle variations, likely due to reduced airfoil efficiency in low-Re regimes. Consequently, higher average power losses occur when DIC mode is active. Such behaviour has been observed in previous wind tunnel studies with comparable model turbines (e.g. Frederik et al., 2020b; van der Hoek et al., 2022, 2024). Nevertheless, the findings highlight the potential wind farm power benefits of DIC implementation in realistic inflow conditions, particularly in low-turbulence environments, which typically exhibit more persistent wakes.

Furthermore, it is worth noting that the optimal wind farm power gains are predominantly achieved with WT1 actuation at St=0.30 and A=2°. This aligns closely with the optimal Strouhal number identified in previous wind tunnel studies using a three-turbine configuration (Frederik et al., 2020b; Wang et al., 2020). Although the optimal gains with low amplitude (A=1°) are achieved at St=0.40, the net power gains remain similar to those obtained with St=0.30. This suggests that adopting a single Strouhal number could simplify integration into a real wind farm controller while providing comparable benefits. In line with wake recovery trends, a greater impact on power gains is observed with increased pitch amplitude rather than increased St. While this study was limited to two amplitude cases, it can be inferred that the maximum DIC amplitude should be constrained to limit structural loads, as recommended for the helix approach (Taschner et al., 2023). Accordingly, future studies should explore the trade-offs between power benefits and structural-load penalties. For instance, Frederik and van Wingerden (2022) reports that DIC primarily affects the tower fore–aft bending moment, without introducing additional risk to the pitch bearing compared to conventional individual pitch control (IPC) for load alleviation. To further investigate load impacts, wind tunnel experiments with aeroelastic model wind turbines capable of meaningful load analysis would be valuable. Additionally, assessing the robustness of optimal control parameters under dynamic inflow conditions, such as varying wind direction, turbulence intensity, and wind speeds, remains a key aspect for future research.

5 Conclusions

This study investigated the potential of DIC to improve wake recovery in single- and two-turbine configurations, as well as potential wind farm power gains in a virtual three-turbine configuration. This encompassed experiments under baseline uniform inflow and two realistic ABL inflow conditions. WindScanner measurements enabled detailed analysis of WT1's wake recovery at different pitch amplitudes $A\in \mathit{\{}\mathrm{1}\mathit{°},\mathrm{2}\mathit{°}\mathit{\}}$ and Strouhal numbers $St\in \mathit{\{}\mathrm{0.25},\mathrm{0.30},\mathrm{0.40}\mathit{\}}$, along with its cascading effects on the wake of a downstream turbine WT2 operating in greedy mode. Compared to the baseline greedy mode, the results showed improved wake recovery of both WT1 and WT2 solely through WT1 actuation. This improvement persisted across all DIC cases and inflow scenarios, yet the degree of DIC-added recovery decreased with increasing inflow turbulence. The study also provided insights into the interplay between optimal excitation frequency and pitch amplitude. Notably, stronger control authority was achieved by increasing pitch amplitude rather than Strouhal number, as higher amplitudes produced a faster turbulence build-up and transition to the far-wake region. Within the considered range, optimal gains were observed at higher Strouhal numbers for lower pitch amplitudes, and vice versa. This was evidenced by both WindScanner wake measurements and WT2's power output. Furthermore, the study demonstrated wind farm power gains not only under uniform inflow but also under turbulent and sheared inflow. Overall, these findings support DIC's potential as a promising wind farm flow control strategy, demonstrating consistent benefits and adaptability under realistic inflow conditions.

Future research should include fatigue load analyses to balance power gains with structural-load penalties, as increased pitch parameters, either independently or together, may exacerbate fatigue loading and power losses at the actuated turbine. Further exploration of DIC under dynamic inflow conditions could also extend its applicability or potential integration with more advanced strategies, such as wake steering control.

Appendix A: WindScanner measurement uncertainty

To illustrate the uncertainty in wake measurements obtained with the lidar WindScanner, Fig. A1a–c presents contours of the relative error ($e_u/u$) introduced by the single-Doppler reconstruction of u at downstream distances $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{5},\mathrm{9}\mathit{\}}$, while Fig. A1d–f shows the corresponding statistical uncertainty at the same locations. The displayed contours correspond to experiments under uniform inflow with WT1 actuation at St=0.30 and A=2°. The analysis of $e_u/u$ follows the standard uncertainty propagation method (van Dooren et al., 2017; Hulsman et al., 2022b), expressed as

$$\begin{array}{}\text{(A1)}& e_u=\sqrt{{\left({\displaystyle \frac{\partial u}{\partial v_{\text{los}}}}{\mathit{\delta }}_{v_{\text{los}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial u}{\partial v}}{\mathit{\delta }}_v\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial u}{\partial w}}{\mathit{\delta }}_w\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial u}{\partial \mathit{\varphi }}}{\mathit{\delta }}_{\mathit{\varphi }}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial u}{\partial \mathit{\theta }}}{\mathit{\delta }}_{\mathit{\theta }}\right)}^{\mathrm{2}}},\end{array}$$

where ${\mathit{\delta }}_{v_{\text{los}}}$ is the uncertainty of the measured line-of-sight wind speed, assumed to be 1 % of u_∞. δ_v and δ_w represent the uncertainties arising from neglecting the v and w components, conservatively assumed as 1 m s⁻¹. δ_ϕ and δ_θ refer to the uncertainties in the azimuth and elevation angles, each assumed to be 0.5 mrad. Additionally, the statistical uncertainty is expressed in terms of the margin of error $e_{\mathrm{MOE}}=z_{\mathit{\gamma }}\mathit{\sigma }/\sqrt{N}$, where z_γ=1.96 is the quantile corresponding to a 95 % confidence interval, σ is the standard deviation of the measurements, and N is the sample size.

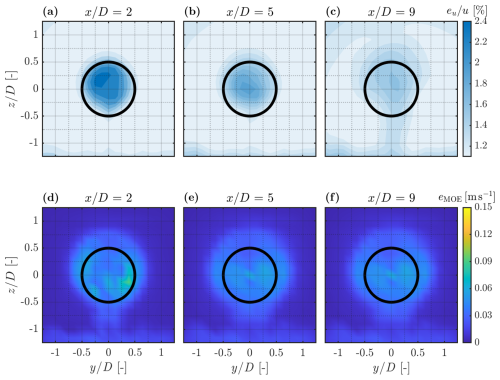
Figure A1 Uncertainty in the streamwise velocity component measured with the WindScanner at downstream distances $x/D$ ∈ $\mathit{\{}\mathrm{2},\mathrm{5},\mathrm{9}\mathit{\}}$. The top row (a–c) shows the relative error ($e_u/u$) introduced by the single-Doppler reconstruction, while the bottom row (d–f) presents the statistical margin of error (e_MOE). All wake contours correspond to experiments under uniform inflow with upstream turbine actuation at St=0.30 and A=2°.

In general, $e_u/u$ is higher within the wake and closer to the rotor, since the wind speed deficit is more pronounced. Similarly, a higher e_MOE is observed in regions of higher turbulence due to increased fluctuations within the wake.

Appendix B: Wind speed deficit profiles

To illustrate the differences among DIC cases with increasing Strouhal number, $St\in \mathit{\{}\mathrm{0.25},\mathrm{0.30},\mathrm{0.40}\mathit{\}}$, Fig. B1 presents horizontal wake profiles of WT1. Each row depicts the wind speed deficit at hub height ($\mathrm{1}-u/u_{\mathrm{\infty }}$) across different inflow conditions at downstream locations $x/D\in \mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5}\mathit{\}}$. Similarly, Fig. B2 displays wind speed deficit profiles of WT2, comparing cases with and without WT1 actuation at downstream locations $x^{\prime }/D\in \mathit{\{}\mathrm{2},\mathrm{4}\mathit{\}}$.

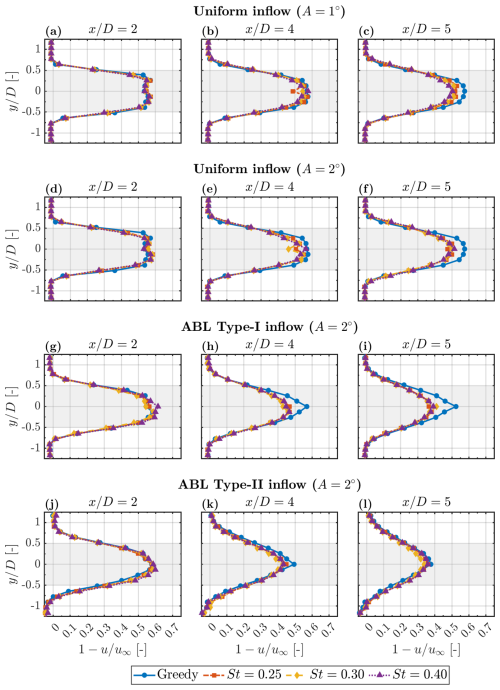
Figure B1 Horizontal wake profiles of WT1 showing the wind speed deficit at hub height ($\mathrm{1}-u/u_{\mathrm{\infty }}$) under greedy and DIC cases. Each row corresponds to a different inflow type at downstream distances $x/D\in \mathit{\{}\mathrm{2},\mathrm{4},\mathrm{5}\mathit{\}}$. Shaded grey regions indicate the rotor swept area.

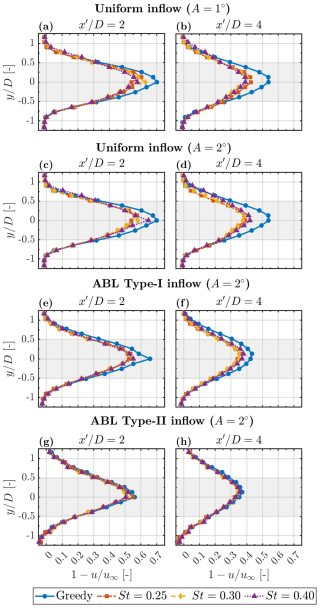
Figure B2 Horizontal wake profiles of WT2 showing the wind speed deficit at hub height ($\mathrm{1}-u/u_{\mathrm{\infty }}$). In all cases, WT2 remains in greedy operation, while WT1 alternates between greedy and DIC modes. Each row corresponds to a different inflow type at downstream distances $x^{\prime }/D\in \mathit{\{}\mathrm{2},\mathrm{4}\mathit{\}}$. Shaded grey regions indicate the rotor swept area.

Appendix C: Validation of wind farm power gain trends

To validate the qualitative trends observed in Fig. 14, a virtual three-turbine configuration is considered, where only WT1 is based on power measurements, while WT2 and WT3 are virtual turbines whose power is estimated from u_REWS following the method outlined in Sect. 3.3. This approach eliminates the influence of Re on aerodynamic efficiency (C_P) of the model turbine, isolating the effect of DIC on wake recovery and downstream performance. Figure C1 presents the corresponding mean power ratio ($P_i/P_{\mathrm{ref}}$) for individual turbines and the overall wind farm. While the relative magnitude of power gains changes slightly compared to the real–real–virtual configuration used in the main analysis, the qualitative trends remain consistent.

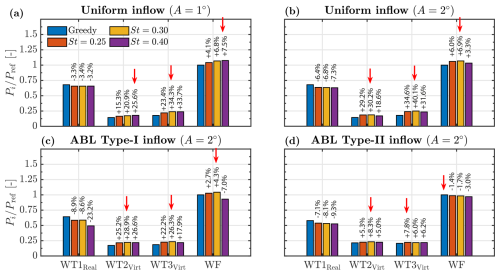
Figure C1 Validation of wind farm power gain trends using a real–virtual–virtual turbine configuration. The power ratio ($P_i/P_{\mathrm{ref}}$) is shown for individual turbines (WT1, WT2, WT3) and the wind farm (WF), with WT1 operating in both greedy and DIC modes, while virtual WT2 and virtual WT3 remain in greedy mode. Each subchart corresponds to a different inflow condition. Percentage values indicate the relative change with respect to the baseline greedy case, with P_ref representing the wind farm power with all turbines in greedy mode. Red arrows highlight the optimal gains.

Appendix D: Power detriment in a full-scale actuated turbine

To address the high power losses experienced by the model wind turbine due to DIC activation, aeroelastic simulations are performed in OpenFAST v3.4.1 (National Renewable Energy Laboratory, 2023) using the full-scale NREL-5 MW reference turbine (D= 126 m). To account for unsteady aerodynamic effects, the Beddoes–Leishman unsteady aerodynamic model is employed. All simulations are conducted at u_∞= 7 m s⁻¹ to match the wind tunnel conditions. TurbSIM (National Renewable Energy Laboratory, 2009) is used to generate ABL inflows with the same power-law exponent and turbulence intensity values described in Sect. 2.5. Table D1 summarises the 10 min averaged power losses experienced by the actuated turbine relative to the baseline greedy case. In general, DIC cases at A=2° exhibit power losses below 1.6 % across all inflow conditions, decreasing to around 0.4 % at A=1°. Therefore, despite some simplifications inherent in OpenFAST simulations, the results provide reasonable indication that power losses in full-scale turbines are likely smaller than those experienced by the model turbine.

Table D1 Power loss at WT1 due to DIC relative to the greedy case, shown as a function of pitch amplitude and Strouhal number across different inflow conditions. Results are based on OpenFAST simulations using the NREL-5 MW reference turbine (D=126 m).