Drop-size-dependent effects in leading-edge rain erosion and their impact on erosion-safe mode operation

Leading-edge rain erosion poses a significant challenge for the wind turbine industry due to its detrimental effects on structural integrity and annual energy production. Developing effective mitigation strategies requires understanding the precipitation conditions driving erosion. The influence of the rain droplet diameter on both the formation of erosion damage and erosion mitigation strategies has yet to be sufficiently understood. This study proposes an enhanced damage model based on the impingement metric as used in the state of the art but improved by including important and thus far neglected physical mechanisms such as the recently described droplet slowdown and deformation effect. Several drop-size-dependent effects are identified within the damage model. Subsequently, their significance for leading-edge erosion is established for the International Energy Agency (IEA) 15 MW reference wind turbine, a site in the Netherlands and a commercial leading-edge coating. Thereafter, the influence of the drop-size effects on the viability of the erosion-safe mode (ESM) is investigated. The outcome is that drop-size effects strongly impact the erosion process and should not be neglected during modeling. Large droplets are considerably more damaging than small droplets, even when normalized for water volume. This directly influences the parameter space of erosion, such as the relevant droplet diameter range that should be studied. The drop-size effects shift damage production to higher rain intensities. Roughly half of the erosion damage is produced by only 10 % of rain events. When drop-size effects are excluded, this value shifts to more than 20 %. Regarding the ESM, we found that it can be utilized up to twice as efficiently when drop-size effects are adequately modeled. The findings highlight the criticality of drop-size effects in rain erosion modeling for wind turbine blades, impacting lifetime predictions, ESM viability and the parameter space of leading-edge erosion. This paper also provides a formal derivation of impingement and describes a method for finding optimal ESM strategies.

1 Introduction

Leading-edge rain erosion is the process of material removal from wind turbine blades by impact with rain droplets. Erosion leads to roughening of the blade's leading edge. Depending on the turbine and site conditions, an eroded blade might need to be repaired frequently to avoid the progression of damage deep into the structural layers of the blade. The blade roughening disturbs the boundary layer and causes an earlier transition from laminar to turbulent flow (Campobasso et al., 2023). This can lead to a reduction in annual energy production (AEP) in the range of up to several percent (Papi et al., 2021; Campobasso et al., 2023; Castorrini et al., 2023; Barfknecht et al., 2022). Due to the combination of maintenance costs and performance loss, leading-edge rain erosion constitutes a significant problem for wind farm operators.

As a reaction, numerous mitigation strategies have been devised. Examples include protective tape (Traser et al., 2019), soft shells (Mishnaevsky et al., 2021) and hard shells (Mathew et al., 2022). The recently proposed erosion-safe mode (ESM) represents an operational mitigation strategy against erosion (Bech et al., 2018; Picard and Canal Vila, 2019). In ESM operation, the turbine's rotational speed is lowered during precipitation events to avoid erosion damage. If carried out effectively, the ESM has the potential to fully protect the turbine from erosion damage. However, limiting the turbine's rotational speed leads to a reduction in AEP and, thus, performance loss as well. Barfknecht et al. (2022) have shown that depending on the rain frequency and the site mean wind speed, the ESM can lead to a lower AEP loss compared to a mildly eroded blade (or an equipped blade protection system that creates similar losses; see the recent results of Bak et al., 2023).

Understanding the conditions that promote the development of erosion is fundamental to developing and applying any mitigation strategy, whether in the form of protective solutions or operational adjustments. The parameter space of erosion is vast: turbines have varying tip speeds, the wind conditions differ according to the site and so does the precipitation. Rain is heterogeneous. It is composed of droplets of varying diameters. The statistical distribution of the rain droplets is described with a drop-size distribution, with typical choices being the Best or Marshall–Palmer distributions. In practice, the drop-size distribution is site-dependent (Pryor et al., 2022). Determining the erosivity of a rain event requires knowledge about the drop-size distribution and the erosion damage associated with every droplet diameter.

So far, there is still considerable uncertainty regarding how the diameter influences the erosivity of droplets. It is also unknown whether the implementation and viability of the ESM might be affected by this lack of knowledge. Bech et al. (2022) performed measurements on an erosion test rig. They found that depending on the impact speed, either smaller or larger diameters are more damaging. Verma et al. (2020) performed numerical simulations in which a water droplet impacts a composite target. They found that the maximum coating stress increases with the droplet size. Amirzadeh et al. (2017) performed similar simulations but assumed that the impact target was solid. In contrast to Verma et al. (2020), they found that the maximum impact pressure is invariant with the droplet diameter. In Barfknecht and von Terzi (2023), it was shown that droplets in the proximity of wind turbine blades are expected to slow down. Their analysis suggests that large droplets are significantly more damaging than small droplets.

The present study investigates the following two research questions.

1. How does the drop size influence the erosivity?

2. Is a thorough understanding of drop-size effects important for the design of the erosion-safe mode?

The term drop-size effect refers to physical processes where the droplet diameter influences the erosivity, especially those effects that persist even when accounting for droplet volume or mass. To answer these research questions, a turbine, a site and a leading-edge material must be considered. In this study, a typical combination of these is chosen. Therefore, some results might only pertain to this particular combination. In this study, the International Energy Association (IEA) 15 MW reference turbine is used (Gaertner et al., 2020). Where applicable, results for the non-dimensional blade span $r/R_{\text{blade}}=\mathrm{0.9}$ are shown. This location was chosen based on the fact that leading-edge protection solutions are generally applied on a length of 10 to 20 m when measured from the tip (Verma et al., 2021). The blade span of the IEA 15 MW is approximately 120 m. The turbine was assumed to be located at the coastal site De Kooy (Den Helder) in the Netherlands at the coordinates 52°55^′26.4" N, 4°46^′48.0" E.

The paper is organized into two parts. Each part pertains to one research question. Attached to this paper is an extensive appendix that develops and formalizes concepts that are used in this study but are not directly linked to the research questions. The first part starts in Sect. 2.1 by developing an erosion damage model based on the impingement metric. Subsequently, in Sect. 2.2, the drop-size effects contained in the model are identified, and their relevance is quantified for each effect individually. In Sect. 2.3, the drop-size effects are analyzed holistically and combined to find an answer to the first research question. Section 2.4 synthesizes the results in preparation for the second research question. The second part, presented in Sect. 3, establishes the influence of drop-size effects on the implementation and viability of the ESM. The conclusions of this paper are presented in Sect. 4. Appendix A gives a formal derivation of the impingement damage metric. In Appendix B, the operational regime of the ESM is defined together with a method to derive optimal ESM strategies. In Appendix C, the calculation of the AEP and pitch angle is explained.

2 Drop-size-dependent effects

The methodology of this section consists of two main parts. First, this study's damage model is derived. It is used to calculate the lifetime of the the blade under various operating conditions. In the second part, the drop-size effects that are contained within the damage model are identified and discussed.

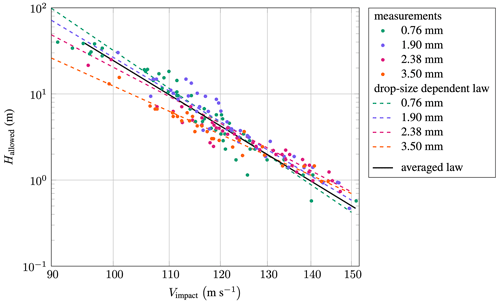
Figure 1 Erosion test-rig results and the drop-size-dependent damage law by Bech et al. (2022) that relate impact velocity to impingement. The averaged law by Barfknecht and von Terzi (2023) is also given; note that the figure is a log–log plot.

2.1 Derivation of the damage model

2.1.1 Damage rule and metric

The damage model is built on the linear Palmgren–Miner damage rule. The damage metric that is used is impingement H. It represents the water column that is caught by the wind turbine's blade during operation. One obtains

$$\begin{array}{}\text{(1)}& D=T_{\text{rain}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}\mathit{°}}{\overset{\mathrm{360}\mathit{°}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{{\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}}{H_{\text{allowed}}}}\mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }\mathrm{d}{V}_{\text{wind}}\mathrm{d}I,\end{array}$$

where D is the damage accumulated in 1 year of operation. H_allowed is the impingement that can be collected by the blade before damage can be observed on the blade's coating. ${\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}$ is the rate at which impingement is collected during operation. ∂_t is a shorthand notation for the operator $\partial /\partial t$. A detailed derivation of impingement is given in Appendix A1. T_rain is the duration of rain during a year and is given by

$$\begin{array}{}\text{(2)}& T_{\text{rain}}=T_{\text{year}}{p}_{\text{rain}},\end{array}$$

where T_year is the time in a year and p_rain is the probability of rain at the wind turbine site. For De Kooy in the Netherlands, p_rain = 6.7 % (KNMI, 2020).

The equation integrates over four statistically distributed variables: the rain intensity I, the wind speed V_wind, the blade's rotational position θ and the rain droplet size ϕ. The equation assumes an elastic behavior of the leading-edge material. The lifetime in years is

$$\begin{array}{}\text{(3)}& L={\displaystyle \frac{\mathrm{1}}{D}}.\end{array}$$

In this study the continuous integrals were discretized and integrated numerically using the trapezoidal rule. The discretization was performed carefully so that the results are grid converged with respect to the significant digits.

2.1.2 Impingement until the end of incubation

The impingement that can be collected by the blade until the end of the incubation period (allowed impingement) is modeled using a power law.

$$\begin{array}{}\text{(4)}& H_{\text{allowed}}={\displaystyle \frac{\mathit{\alpha }}{V_{\text{impact}}^{\mathit{\beta }}}},\end{array}$$

where α and β are two coefficients, and V_impact is the water droplet impact velocity with the blade. Here α is not an angle. Instead of determining these parameters from, e.g., a semi-empirical relation as used in the Springer model (Hoksbergen et al., 2022), we choose to determine the parameters directly from experimental data instead. Bech et al. (2022) performed tests of a commercial polyurethane-based leading-edge coating in a rotating-arm test rig. The coating was subjected, in independent tests, to four different droplet sizes of 0.76, 1.90, 2.38 and 3.50 mm. The 0.76 mm droplets were created by spraying, leading to a variance in the diameter of the produced droplets. This is discussed in more detail in the original reference. The test rig with its test specimen was stopped at regular intervals, and new damage spots were recorded. Most damage was observed directly at the leading edge. It was, therefore, assumed that Eq. (4) gives the allowed impingement for droplets colliding head-on. The resulting measurements are shown as points in Fig. 1. From these, two damage laws are derived.

Averaged law. The averaged law is obtained by fitting a curve through the measurements of Bech et al. (2022). It was first described in Barfknecht and von Terzi (2023). The resulting curve is shown in Fig. 1. The averaged model serves as a baseline for comparing the drop-size-dependent law. The best-fit parameters are

$$\begin{array}{}\text{(5)}& \mathit{\alpha }=\mathrm{3.4860}\times {\mathrm{10}}^{\mathrm{20}},\mathit{\beta }=\mathrm{9.5774}.\end{array}$$

Drop-size-dependent law. The drop-size-dependent law is directly taken from Bech et al. (2022). It accounts for drop-size-dependent performance differences in the coating by utilizing a heuristic softsign function. It reads

$$\begin{array}{}\text{(6)}& H_{\mathrm{100}}={\displaystyle \frac{a\mathrm{\Delta }\mathit{\varphi }}{\mathrm{1}+\left|\mathrm{\Delta }\mathit{\varphi }\right|}}+b,\end{array}$$

with $\mathrm{\Delta }\mathit{\varphi }=\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{0}}$, ϕ₀ = 2.3 mm, $a=-\mathrm{17.1}$ and b=21.7. Further,

$$\begin{array}{}\text{(7)}& \mathit{\beta }={\displaystyle \frac{a\mathrm{\Delta }\mathit{\varphi }}{\mathrm{1}+\left|\mathrm{\Delta }\mathit{\varphi }\right|}}+b,\end{array}$$

with $a=-\mathrm{3.1}$, b=8.9 and ϕ₀ = 2.1 mm. ϕ needs to be substituted in millimeters. α is given by

$$\begin{array}{}\text{(8)}& \mathit{\alpha }={\mathrm{100}}^{\mathit{\beta }}{H}_{\mathrm{100}}.\end{array}$$

Like the averaged law, it is visualized in Fig. 1.

It should be noted that the parameters of both laws depend on the leading-edge material considered. Therefore, other materials might behave differently, especially with respect to the drop size. The authors of this study consider the results from Bech et al. (2022) to be the best-available erosion test-rig data set in the public domain and view them as a good representation of the current state of the art.

2.1.3 Calculation of the accumulated impingement

The impingement rate is the last missing term in Eq. (1) that needs to be defined. It is given by

$$\begin{array}{}\text{(9)}& {\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}=\underset{\text{T1}}{\underbrace{{\displaystyle \frac{I{f}_{\mathit{\varphi },\text{plane}}}{V_{\mathit{\varphi }}}}}}\underset{\text{T2}}{\underbrace{V_{\text{collection}}}}{f}_{\mathrm{I}}{f}_{V_{\text{wind}}}{f}_{\mathit{\theta }},\end{array}$$

where V_collection is the speed at which rain is accumulated, and V_ϕ is the droplet terminal fall velocity. Note that the dimension of ${\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}$ is [LT⁻¹]. The derivation and additional clarification of Eq. (9) is provided in Appendix A1. T1 represents the volume of water per volume of air, and T2 represents the swept line (volume) of air per unit of time. It is dependent on four statistically distributed variables that will be discussed in the following.

The first distribution f_ϕ,plane should not be interpreted as a time fraction but rather stems from the fact that at every instant in time, a wide range of droplet sizes impact on the blade. In particular, it describes the amount of water associated with every droplet diameter that passes through an imaginary plane in the air. In this study f_ϕ,plane is derived using the Best drop-size distribution (Best, 1950a). Best gives a probability density function (PDF) that describes the water mass associated with every droplet diameter in a volume of air. It reads

$$\begin{array}{}\text{(10)}& f_{\mathit{\varphi },\text{air}}=\mathrm{2.25}{\left({\displaystyle \frac{\mathrm{1}}{\mathrm{1.3}{I}^{\mathrm{0.232}}}}\right)}^{\mathrm{2.25}}{\mathit{\varphi }}^{\mathrm{2.25}-\mathrm{1}}{e}^{-{\left(\frac{{\mathit{\varphi }}_{\mathrm{0}}}{\mathrm{1.3}{I}^{\mathrm{0.232}}}\right)}^{\mathrm{2.25}}}.\end{array}$$

Best's distribution requires the rain intensity I to be given in millimeters per hour, and the droplet diameter ϕ must be substituted in millimeters. To convert the distribution into f_ϕ,plane, the following equation is used:

$$\begin{array}{}\text{(11)}& f_{\mathit{\varphi },\text{plane}}={\displaystyle \frac{f_{\mathit{\varphi },\text{air}}{V}_{\mathit{\varphi }}}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{f}_{\mathit{\varphi },\text{air}}{V}_{\mathit{\varphi }}\mathrm{d}\mathit{\varphi }}}.\end{array}$$

To find the rain intensity distribution f_I, the hourly precipitation data of the automatic Royal Netherlands Meteorological Institute (KNMI) rain gauge station at De Kooy are used. The data from the 10-year window ranging from 2011 to 2020 were used to find the coefficients of f_I in the form of a lognormal distribution. The formula for the lognormal distribution reads

$$\begin{array}{}\text{(12)}& f_{\mathrm{I}}={\displaystyle \frac{\mathrm{1}}{I\mathit{\sigma }\sqrt{\mathrm{2}\mathit{\pi }}}}{e}^{-\frac{(\ln I-\mathit{\mu }{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}.\end{array}$$

The coefficients were found using Matlab's lognfit function. μ is the mean, and σ is the standard deviation. They read σ=0.9693 and $\mathit{\mu }=-\mathrm{0.1987}$ or $\mathit{\mu }=-\mathrm{15.29}$, depending on whether I is considered to be in millimeters per hour or in meters per second.

The distribution of the wind was calculated using a Weibull distribution. It reads

$$\begin{array}{}\text{(13)}& f_{\text{wind}}={\displaystyle \frac{k}{c}}{\left({\displaystyle \frac{V_{\text{wind}}}{c}}\right)}^{k-\mathrm{1}}{e}^{-{\left(V_{\text{wind}}/c\right)}^k},\end{array}$$

where c is the scale parameter, and k is the shape parameter. Both parameters were obtained for the De Kooy location using the Dutch Offshore Wind Atlas at the height of 150 m (DOWA, 2020). They read c = 10.5 m s⁻¹ and k=2.24. The mean wind speed is V_mean = 9.2 m s⁻¹.

Note that it is assumed that the wind speed and the rain intensity are not statistically correlated. In general, this assumption is not true as, e.g., shown in Letson et al. (2020). In the 2011 to 2020 time frame, the De Kooy mean wind speed at 10 m height above ground during rain was 6.80 m s⁻¹, whereas during dry conditions, the mean wind speed was 5.32 m s⁻¹ (KNMI, 2020). However, for the purpose of this study, this assumption is deemed to be acceptable. Results for De Kooy that use actual wind and precipitation measurements as inputs for the ESM are presented in Barfknecht and von Terzi (2024).

The probability density function of the blade position f_θ is given by the equation

$$\begin{array}{}\text{(14)}& f_{\mathit{\theta }}={\displaystyle \frac{\mathrm{1}}{\mathrm{360}\mathit{°}}}.\end{array}$$

During operation, the turbine spins continuously; hence every blade position is equally likely to occur. It is also assumed that during a standstill, the parking position is random.

2.1.4 Calculation of the drop impact velocity

The key driver for the erosion damage is the impact velocity V_impact of the rain droplets. It is used in Eq. (4), where it has a significant effect on the lifetime due to the size of the parameter β. Small variations in the calculated impact velocity will yield very different H_allowed. Secondly, the closely related sibling V_collection is used in Eq. (9) for the calculation of the impingement rate ${\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}$.

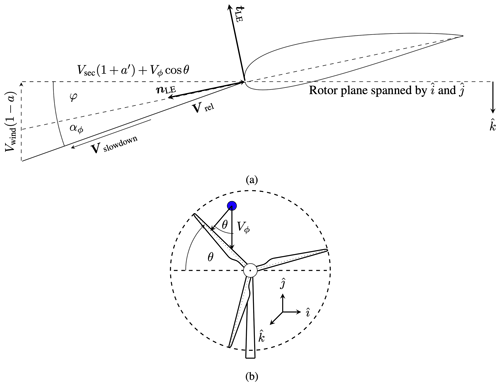
Figure 2 Velocity components and angle definitions that constitute V_impact. (a) Rain droplet velocity components as seen by a blade section, and (b) the definition of the angular blade position θ and its influence on the surface normal component of the terminal droplet velocity V_ϕ.

The following assumptions are made for the derivation of the impact velocity.

• Rain droplets are advected with the local wind vector, which is comprised of the wind speed and the wind turbine's induction factors.

• There are no wind veer, shear, turbulence and gust effects.

• The rotor plane is two-dimensional; i.e., there is no pre-cone and blade bending.

• The blade is rigid.

• The leading edge from root to tip lies in a straight line.

• The droplet slowdown as described in Barfknecht and von Terzi (2023) can be modeled as a one-dimensional problem and the droplets follow a ballistic path. Other assumptions regarding the slowdown effect made in the same reference also apply.

The impact velocity is defined as

$$\begin{array}{}\text{(15)}& V_{\text{impact}}=({\mathit{V}}_{\text{sec}}-{\mathit{V}}_{\text{rain}})\cdot {\mathit{n}}_{\text{LE}},\end{array}$$

where V_sec is the velocity vector of the blade section. V_rain is the velocity vector of the rain (droplets). n_LE is the surface normal vector of the leading edge. Figure 2 visualizes all velocity components that are considered in this study.

Using the velocity diagrams of Fig. 2, one obtains

$$\begin{array}{}\text{(16)}& {\mathit{V}}_{\text{sec}}=\left[\begin{array}{c}\sin \mathit{\theta }{V}_{\text{sec}}\\ \cos \mathit{\theta }{V}_{\text{sec}}\\ \mathrm{0}\end{array}\right]\end{array}$$

and

$$\begin{array}{}\text{(17)}& {\mathit{V}}_{\text{rain}}=\left[\begin{array}{c}-\sin \mathit{\theta }{V}_{\text{sec}}{a}^{\prime }\\ -\cos \mathit{\theta }{V}_{\text{sec}}{a}^{\prime }-V_{\mathit{\varphi }}\\ -V_{\text{wind}}(\mathrm{1}-a),\end{array}\right]-{\mathit{V}}_{\text{slowdown}}\end{array}$$

with

$$\begin{array}{}\text{(18)}& {\mathit{V}}_{\text{slowdown}}=V_{\text{slowdown}}{\displaystyle \frac{-{\mathit{V}}_{\text{rel}}}{\left|{\mathit{V}}_{\text{rel}}\right|}}.\end{array}$$

Inserting into Eq. (15) yields

$$\begin{array}{}\text{(19)}& \begin{array}{rl}{V}_{\text{impact}}=& \left[\begin{array}{c}\sin \mathit{\theta }{V}_{\text{sec}}(\mathrm{1}+a^{\prime })\\ \cos \mathit{\theta }{V}_{\text{sec}}(\mathrm{1}+a^{\prime })+V_{\mathit{\varphi }}\\ V_{\text{wind}}(\mathrm{1}-a)\end{array}\right]\cdot \underset{{\mathit{n}}_{\text{LE}}}{\underbrace{\left[\begin{array}{c}\sin \mathit{\theta }\cos \mathit{\phi }\\ \cos \mathit{\theta }\cos \mathit{\phi }\\ \sin \mathit{\phi }\end{array}\right]}}\\ & +V_{\text{slowdown}}{\displaystyle \frac{-{\mathit{V}}_{\text{rel}}}{\left|{\mathit{V}}_{\text{rel}}\right|}}\cdot \left[\begin{array}{c}\sin \mathit{\theta }\cos \mathit{\phi }\\ \cos \mathit{\theta }\cos \mathit{\phi }\\ \sin \mathit{\phi }\end{array}\right]\end{array}\end{array}$$

$$\begin{array}{}\text{(20)}& \begin{array}{rl}=& V_{\text{sec}}(\mathrm{1}+a^{\prime })\cos \mathit{\phi }+V_{\mathit{\varphi }}\cos \mathit{\theta }\cos \mathit{\phi }\\ & +V_{\text{wind}}(\mathrm{1}-a)\sin \mathit{\phi }-V_{\text{slowdown}}\cos {\mathit{\alpha }}_{\mathit{\varphi }}.\end{array}\end{array}$$

According to Fig. 2a, V_rel is the relative droplet velocity in the plane of the airfoil cross-section considered. In Appendix A2 it is shown that

$$\begin{array}{}\text{(21)}& \begin{array}{rl}{V}_{\text{collection}}=& V_{\text{sec}}(\mathrm{1}+a^{\prime })\cos \mathit{\phi }+V_{\mathit{\varphi }}\cos \mathit{\theta }\cos \mathit{\phi }\\ & +V_{\text{wind}}(\mathrm{1}-a)\sin \mathit{\phi };\end{array}\end{array}$$

hence, the collection velocity is the impact velocity but without the slowdown.

The first two terms in Eq. (20) represent the surface normal component of the circumferential velocity. That is,

$$\begin{array}{}\text{(22)}& V_{\text{circumferential}}=V_{\text{sec}}(\mathrm{1}+a^{\prime })+V_{\mathit{\varphi }}\cos \mathit{\theta },\end{array}$$

with V_sec being the speed of the blade section. At the tip, V_sec=V_tip. a^′ is the radial (tangential) induction factor. In contrast to common inflow velocity diagrams for wind turbines, an extra term reading V_ϕcos θ can be found in Eq. (22). This term represents the velocity component due to the terminal velocity of the rain droplet V_ϕ, as shown in Fig. 2b. It is calculated with the relation from Best (1950b) and reads

$$\begin{array}{}\text{(23)}& V_{\mathit{\varphi }}=\mathrm{9.32}{e}^{\mathrm{0.0405}h}\left(\mathrm{1}-e^{-(\mathrm{0.565}\mathit{\varphi }{)}^{\mathrm{1.147}}}\right).\end{array}$$

It is shown in Fig. 3. h is the height above ground in kilometers and ϕ the droplet diameter in millimeters. The height is

$$\begin{array}{}\text{(24)}& h=h_{\text{hub}}+r\cos \mathit{\theta },\end{array}$$

where h_hub is the turbine's hub height, and r is the position along the blade span. At the tip, r becomes the blade length R_blade, that is r=R_blade.

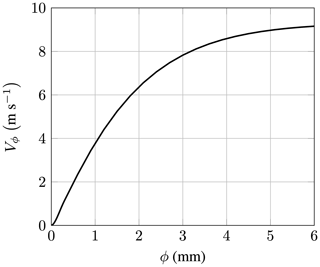
Figure 3 Terminal velocity for falling water droplets as a function of the droplet diameter; values for h = 0 km, i.e., sea level.

The third term of Eq. (20) represents the surface normal component of the inflow velocity. It reads

$$\begin{array}{}\text{(25)}& V_{\text{inflow}}=V_{\text{wind}}(\mathrm{1}-a),\end{array}$$

where V_wind is the wind velocity, and a is the axial induction factor. With the abovementioned assumptions in mind, V_wind is constant throughout the entire rotor plane, and the droplets will be advected perfectly with this velocity.

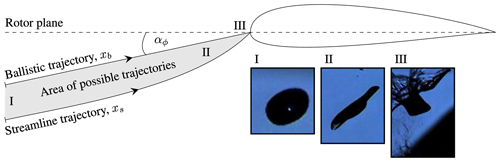
Figure 4 Ballistic and streamline trajectory of a droplet approaching an airfoil (at an angle α_ϕ); φ is set to zero in this illustration. Far away from the blade at station (I), droplets have a shape resembling a spheroid; as the droplets approach the leading edge, they deform (II) and eventually break up into specific breakup patterns (III). The high-speed images are reproduced from Sor et al. (2019); the illustration itself is taken from Barfknecht and von Terzi (2023).

The last term is the so-called slowdown velocity as described in Barfknecht and von Terzi (2023). The velocity field of the airfoil interacts aerodynamically with the rain droplets and, when seen from the airfoil, slows them down, thus making them significantly less erosive. The slowdown results from the velocity differential between the velocity field of the blade and the rain droplet. This creates a drag force, leading to a reduction in velocity. Approaching droplets undergo deformation and can break up, as shown in Fig. 4. The deformation and breakup heavily influence the impact speed of the droplets.

Droplets that impact the leading edge can travel on either a ballistic (in the direction of V_rel) or a streamline trajectory. The latter assumes that the rain droplets follow the flow perfectly, something that should be true for ϕ→ 0 mm. Droplets with diameters of ϕ→∞ mm should follow a ballistic trajectory. This study assumes that the droplets follow a ballistic trajectory. In Barfknecht and von Terzi (2023), it was shown that droplets that follow a streamline trajectory experience more slowdown. Hence, assuming a ballistic trajectory underpredicts the slowdown of small droplets. As will be shown in the remainder, this is a conservative assumption regarding the conclusions of this work.

The slowdown velocity V_slowdown is obtained using the methodology from Barfknecht and von Terzi (2023) where an existing Lagrangian model was extended to accurately predict the velocity of droplets in the vicinity of the leading edge of a wind turbine blade. Two equations of motion are solved that describe the one-dimensional approach of the rain droplets toward the blade:

$$\begin{array}{}\text{(26)}& {\displaystyle }m{\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}x}{\mathrm{d}{t}^{\mathrm{2}}}}& {\displaystyle }=F_{\text{drag}},\text{(27)}& {\displaystyle \frac{\mathrm{3}}{\mathrm{16}}}m{\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}a}{\mathrm{d}{t}^{\mathrm{2}}}}& {\displaystyle }=F_{\mathit{\sigma }}+F_{\mathrm{p}},\end{array}$$

where Eq. (26) represents the deceleration of the droplet, and Eq. (27) describes the droplet's deformation from a spheroid to an oblate spheroid. The method cannot predict the actual (broken-up) droplet shape. However, the results in Barfknecht and von Terzi (2023) showed that approximating the droplet as an oblate spheroid is sufficient to accurately determine the slowdown.

The forces that are acting on the droplet are the drag force F_drag, the surface tension F_σ and the pressure force F_p. F_p drives deformation, while F_σ counteracts droplet deformation. Here, a is the semi-major axis of the oblate spheroid. m is the droplet mass, and x is the droplet position along its path.

The slowdown velocity is then calculated as

$$\begin{array}{}\text{(28)}& V_{\text{slowdown}}={\left({\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\right)}_{\text{at\hspace{0.17em}\hspace{0.17em}impact}}.\end{array}$$

The background velocity V_air field is calculated with

$$\begin{array}{}\text{(29)}& {\displaystyle \frac{V_{\text{air}}}{\left|{\mathit{V}}_{\text{rel}}\right|}}=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{{\left(\mathrm{1}+\frac{\mathrm{\Delta }x}{R_{\mathrm{c}}}\right)}^n}},\end{array}$$

where Δx is the distance between the droplet and blade. At $r/R_{\text{blade}}=\mathrm{0.9}$ the IEA 15 MW turbine has an aerodynamic nose-radius R_c = 0.064 m and an exponent n=1.097 (Barfknecht and von Terzi, 2023). The reader is referred to Barfknecht and von Terzi (2023) for a detailed description of the slowdown model and how to implement it.

The angle φ is

$$\begin{array}{}\text{(30)}& \mathit{\phi }={\mathit{\phi }}_{\text{pitch}}-{\mathit{\phi }}_{\text{twist}},\end{array}$$

where φ_pitch is the pitch angle of the blade. The determination of the pitch angle and the induction factors is described in further detail in Appendix C. φ_twist is the local twist angle. At $r/R_{\text{blade}}=\mathrm{0.9}$, φ_twist = −2.1°. Subsequently, cos α_ϕ can be calculated using

$$\begin{array}{}\text{(31)}& \begin{array}{rl}\cos {\mathit{\alpha }}_{\mathit{\varphi }}& ={\displaystyle \frac{{\mathit{V}}_{\text{rel}}}{\left|{\mathit{V}}_{\text{rel}}\right|}}\cdot {\mathit{n}}_{\text{LE}}\\ & =\cos \left(\arctan \left({\displaystyle \frac{V_{\text{inflow}}}{V_{\text{circumferential}}}}\right)-\mathit{\phi }\right).\end{array}\end{array}$$

It is important to note here that α_ϕ, while similar, is not the angle of attack of the blade element but should rather be considered the drop impact angle. It should also be mentioned that depending on the application, it might be more convenient to write V_impact in its alternative form, that is

$$\begin{array}{}\text{(32)}& V_{\text{impact}}=\cos {\mathit{\alpha }}_{\mathit{\varphi }}\left(\sqrt{V_{\text{inflow}}^{\mathrm{2}}+V_{\text{circumferential}}^{\mathrm{2}}}-V_{\text{slowdown}}\right),\end{array}$$

and concurrently

$$\begin{array}{}\text{(33)}& V_{\text{collection}}=\cos {\mathit{\alpha }}_{\mathit{\varphi }}\sqrt{V_{\text{inflow}}^{\mathrm{2}}+V_{\text{circumferential}}^{\mathrm{2}}}.\end{array}$$

In this study the impact velocity was determined for the leading edge of the blade. It can also be determined for other locations by adjusting the surface normal vector. This can be desirable since, in practice, the point with the highest erosion can lie slightly off the leading edge in the direction of the stagnation point.

On a final note, the careful reader might argue that some droplets get deflected and do not hit the blade and that this aspect is missing. However, in practice, droplets only miss the blade when they tend to follow a streamline trajectory and when that streamline is located toward the top or bottom of the airfoil; see the results of Sor et al. (2021).

Closely related is the concept of collection efficiency, as is known from aircraft icing. For a streamtube, it is the ratio of surface to free-stream water flux, as shown in Gent et al. (2000). Two effects influence this ratio. Firstly, the streamtube can widen toward the airfoil. In the region of the leading edge, the widening merely distributes the rain droplets onto a larger blade area, reducing the surface water flux. Sor et al. (2021) showed that at the leading edge, this reduction is on the order of 10 % for the relevant droplet sizes. The effect becomes more pronounced as droplets become smaller. When moving far away from the leading edge, the widening can, indeed, become so large that some droplets start to miss the blade. Secondly, the collection efficiency is comprised of the reduction in surface water flux due to a non-orthogonal impact with the airfoil's leading edge. This aspect is modeled in this study since (V_sec−V_rain) is projected onto n_LE.

It is important to realize that neglecting the streamtube widening is a conservative assumption regarding the conclusions of this study. The assumptions lead to a higher surface water flux and impingement for smaller droplets. Hence, smaller droplets appear to be more erosive than they actually are. This effect could be included in future works. It, however, necessitates at least Lagrangian particle simulations in a two-dimensional domain, which is computationally costly.

2.2 Discussion of the drop-size effects in the damage model

This section investigates which deductions can be made from the equations within the previously derived damage model. Different drop-size-dependent effects are derived from the model and discussed. In particular, it is shown that due to the drop-size-dependent effects, the damage model suggests the following.

1. Large droplets are more damaging than small droplets.

2. Large droplets become more frequent as the rain intensity increases.

3. As a consequence of the above, for equal amounts of impingement, higher rain intensities are more damaging than lower intensities.

At the core of these deductions is that V_impact and V_collection are the key drivers for erosion. The damage components of Eq. (1) are

$$\begin{array}{}\text{(34)}& {\partial }_t{D}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}={\displaystyle \frac{{\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}}{H_{\text{allowed}}}}.\end{array}$$

Here it is important to realize that V_impact is contained in the denominator and V_collection in the numerator, see Eqs. (4) and (9). Substituting leads to

$$\begin{array}{}\text{(35)}& {\partial }_t{D}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}\propto V_{\text{impact}}^{\mathit{\beta }}{V}_{\text{collection}}\approx V_{\text{impact}}^{\mathit{\beta }+\mathrm{1}}.\end{array}$$

This equation shows that a faster droplet is much more damaging than a slower droplet. First, a high V_collection leads to a higher rate of impingement accumulation. This effect is linear under the assumptions of this study. Secondly, a high V_impact leads to significantly less H_allowed due to the large magnitude of β, which can be on the order of 10. This effect is very severe and highly non-linear.

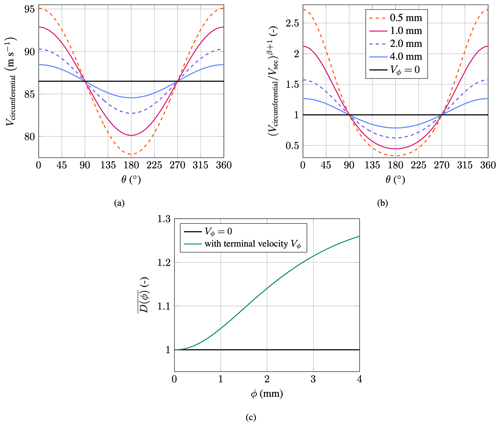
Figure 5 Circumferential velocity and non-dimensional damage as a function of angular blade position for different droplet diameters; the induction factors were neglected (β=9.58; V_sec = 86.5 m s⁻¹): (a) circumferential velocity, (b) non-dimensional damage and (c) average damage over one blade rotation.

2.2.1 Influence of the rotation and terminal velocity on the impact velocity

The terminal velocity of rain droplets causes an oscillation in impact speed over one blade rotation. In Eq. (22), the surface normal component of the droplet terminal velocity is not constant over one blade rotation but is a function of cos θ. The influence of θ on V_{circumferential} is shown in Fig. 5a. V_{circumferential} is at a maximum at θ = 0°, i.e., when the blade-section speed and the droplet's terminal velocity directly oppose each other. Correspondingly, V_{circumferential} is at a minimum at θ = 180°. Since the droplet terminal velocity is a function of the droplet diameter, as shown in Fig. 3, this effect becomes more pronounced as the droplet diameter increases. It is noteworthy that the circumferential velocity averaged over one rotation is constant. However, due to the highly non-linear character of Eq. (35), some impacts at a lower and some impacts at a higher impact speed will, in total, yield higher damage. Figure 5b plots the non-dimensional damage $(V_{\text{circumferential}}/V_{\text{sec}}{)}^{\mathit{\beta }+\mathrm{1}}$ over one blade rotation. Here it is assumed that there are no induction factors, V_slowdown=0 and V_wind=0. At θ = 90° and θ = 270°, the surface normal component of the terminal velocity is zero. Hence, the normalized damage is unity since V_{circumferential}=V_sec. The maximum damage is found at θ = 0° and the minimum at θ = 180°, coinciding with the locations of maximum and minimum V_{circumferential}. The non-dimensional average damage over one rotation as a function of droplet diameter is shown in Fig. 5c. It reads

$$\begin{array}{}\text{(36)}& \stackrel{\mathrm{‾}}{D\left(\mathit{\varphi }\right)}=\underset{\mathrm{0}}{\overset{\mathrm{360}}{\int }}{f}_{\mathit{\theta }}{\left({\displaystyle \frac{V_{\text{circumferential}}}{V_{\text{sec}}}}\right)}^{\mathit{\beta }+\mathrm{1}}\mathrm{d}\mathit{\theta }.\end{array}$$

The damage is 1.013 for a droplet of 0.5 mm and 1.260 for a droplet of 4.0 mm, so the 4 mm droplet creates about 24.4 % more damage. This shows that the effect is significant and needs to be accounted for.

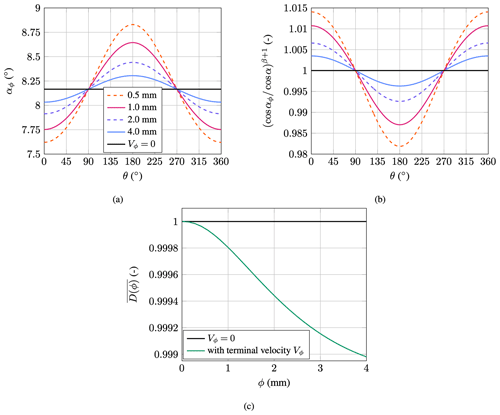
Figure 6 Impact angle and non-dimensional damage as a function of angular blade position for different droplet diameters; the induction factors were neglected (β=9.58, V_sec = 86.5 m s⁻¹, V_wind = 9.2 m s⁻¹, ${\mathit{\phi }}_{\text{twist},r/R_{\text{blade}}=\mathrm{0.9}}$ = −2.10°, ${\mathit{\phi }}_{\text{pitch},\mathrm{9.2}\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}}$ = 0°): (a) impact angle, (b) non-dimensional damage and (c) average damage over one blade rotation.

2.2.2 Influence of the rotation and terminal velocity on the impact angle

The drop impact angle α_ϕ varies with the blade position because it depends on V_{circumferential}; see Eq. (31). During the upstroke of the blade, the term V_ϕcos θ is positive and decreases the angle α_ϕ. During the downstroke, the sign becomes negative and α_ϕ increases. The variation in α_ϕ becomes stronger as the droplet diameter increases. α_ϕ is shown in Fig. 6a. It can be decomposed into

$$\begin{array}{}\text{(37)}& {\mathit{\alpha }}_{\mathit{\varphi }}=\mathit{\alpha }+\mathit{\alpha }(\mathit{\theta }{)}^{\prime }.\end{array}$$

The impact angle is, therefore, a combination of the classical angle of attack of the blade and an oscillating component that is dependent on the angular blade position θ.

Equations (32) and (35) imply that

$$\begin{array}{}\text{(38)}& {\partial }_t{D}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}\propto \cos ({\mathit{\alpha }}_{\mathit{\varphi }}{)}^{\mathit{\beta }+\mathrm{1}}.\end{array}$$

This equation is shown in its non-dimensional form in Fig. 6b. As before, the damage oscillates once over one single rotation. On first glance, Fig. 6b appears to be similar to Fig. 5b. During the upstroke, the damage production is increased, whereas during the downstroke of the blade, the damage is reduced. However, the magnitude of the effect is very small, with the amplitude being only about 1.5 % for a droplet of 4 mm in diameter. Calculating similarly to Eq. (36), the averaged non-dimensional damage over one rotation yields Fig. 6c. The damage is approximately unity for a droplet of 0.5 mm and about 0.999 for a droplet of 4.0 mm. Hence, a slight reduction in the damage can be observed due to α^′ being asymmetrical to the blade position, i.e., for a droplet of 4 mm diameter α(0°)^′ = −0.54° and α(180°)^′ = 0.66°. However, considering that the averaged damage is near unity for all droplet diameters, one can conclude that this effect is not significant and can be neglected.

2.2.3 Drop-size-dependent damage law

The drop-size-dependent damage law of Bech et al. (2022) suggests that the performance of a wind turbine coating is dependent on the droplet diameter. The law is given by Eqs. (6)–(8) and is plotted for four different droplet diameters in Fig. 1. The spread in the curves for small and large droplets closes with increasing impact speed. At about 116 m s⁻¹, a crossover point exists. At that point, droplets of 0.76 and 1.90 mm have the same H_allowed. Beyond that point, smaller droplets become more damaging than larger droplets. As the impact speed increases, the spread starts to grow again. For diameters above approximately 2 mm, the crossover point is delayed to higher speeds, where the exact location is dependent on the particular diameter.

The drop-size dependency is shown in more detail in Fig. 7. The figure shows the natural logarithm of H_allowed for a combination of relevant droplet sizes and impact speeds. The shape of the softsign function is clearly visible within the contour plot. The allowed impingement drops sharply above diameters of about 1 mm and continues with a steep decline up to 3 mm, where it then starts to slowly become shallower again. The drop-size effect is significant, which can be seen by following a contour. A small droplet ϕ→ 0 mm has the same allowed impingement at 85 m s⁻¹ as a 4 mm droplet at about 65.6 m s⁻¹. When considering a constant impact speed of 85 m s⁻¹, a droplet ϕ→ 0 mm has an allowed impingement of 201 m, while a 4 mm droplet will already lead to failure after 34 m of impingement.

Figure 7 Contour lines of ln (H_allowed) according to Eqs. (6)–(8) for different droplet diameters and impact velocities. Contour levels are spawned at ϕ→ 0 mm for impact velocities in 5 m s⁻¹ increments.

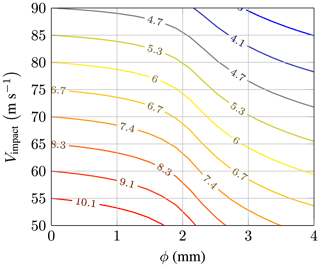
α and β govern the drop-size dependency. As the droplet diameter decreases, α increases, leading to a longer lifetime for small droplets at low impact speeds. Further, as the droplet diameter decreases, β increases, resulting in smaller droplets having a higher sensitivity (slope) with respect to the impact velocity. Consequently, H_allowed for small droplets starts high but decreases rapidly with increasing impact speeds. In contrast, for large droplets, H_allowed is initially lower but decreases more gradually. These differing behaviors cause the curves for small and large droplets to intersect. The first crossover point occurs at approximately 116 m s⁻¹, which is above the typical impact speeds encountered in current wind turbine applications. Therefore, under these conditions, the damage law suggests that small droplets cause less damage than larger ones.

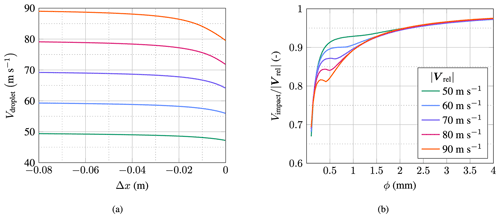
Figure 8 Relative velocity before impact and non-dimensional impact velocity for droplets approaching the leading edge of an airfoil; plot is reproduced from Barfknecht and von Terzi (2023); (a) relative velocity of 0.49 mm diameter droplets versus distance to the leading edge Δx, (b) non-dimensional impact velocity as a function of droplet diameter.

2.2.4 Droplet slowdown

Rain droplets slow down when approaching the leading edge of an airfoil, as shown in Fig. 8a. It can be seen that the slowdown for droplets of 0.49 mm in diameter approaching at 90 m s⁻¹ is about 10 m s⁻¹. The figure also shows that most of the slowdown is taking place close to the leading edge. In this particular case, most of the slowdown is happening at a distance of less than 5 cm to the leading edge. The slowdown is influenced by $\left|V_{\text{rel}}\right|$ and the droplet size. As $\left|V_{\text{rel}}\right|$ increases, so does the slowdown velocity. This is shown in Fig. 8a. Figure 8b shows that smaller droplets encounter significantly more slowdown than larger ones.

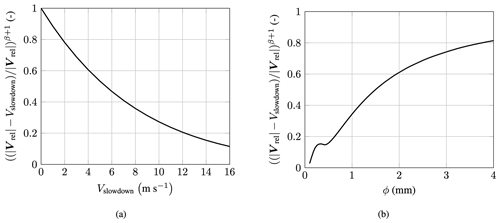
Figure 9 Non-dimensional damage due to the slowdown effect versus slowdown velocity (a) and droplet diameter (b): β=9.58, $\left|{\mathit{V}}_{\text{rel}}\right|$ = 86.5 m s⁻¹, R_c = 0.064 m and n=1.097.

The damage reduction due to the slowdown effect is visualized in Fig. 9. Due to the high sensitivity of the damage law, a moderate slowdown of 5.5 m s⁻¹ reduces the erosion damage already by half. The figure also shows the damage reduction that is associated with different droplet diameters. The slowdown effect suggests a damage reduction of about 20 % for droplets of 4 mm. For droplets of 0.5 mm, a damage reduction of 84 % is predicted. Hence, the slowdown is highly drop-size-dependent and overall leads to a significant reduction in the absolute erosion damage.

2.3 Composition of the total erosion damage

With the damage model described and the drop-size effects identified, the total erosion damage can be calculated for the considered sample site and turbine. Subsequently, it can be decomposed into its components to quantify the influence of the drop-size effects. The damage is decomposed with respect to the droplet diameter, the angular position of the blade, the wind speed and the rain intensity. Equation (1) can be modified into

$$\begin{array}{}\text{(39)}& D\left(\mathit{\varphi }\right)=T_{\text{rain}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{360}}{\int }}{\partial }_t{D}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}\mathrm{d}\mathit{\theta }\mathrm{d}{V}_{\text{wind}}\mathrm{d}I.\end{array}$$

Then D(ϕ) is normalized into f_D(ϕ) so that

$$\begin{array}{}\text{(40)}& \underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_D\left(\mathit{\varphi }\right)\mathrm{d}\mathit{\varphi }=\mathrm{1}.\end{array}$$

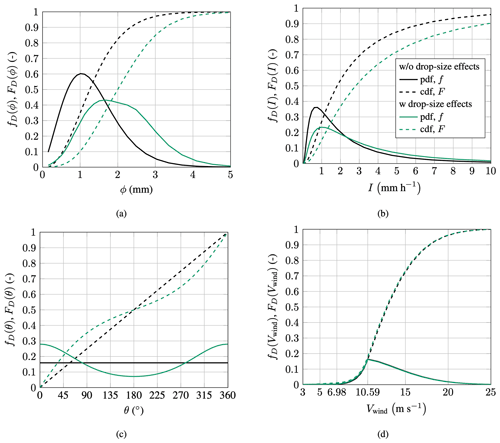
Figure 10 Composition of the normalized erosion damage with respect to the four independent variables for the IEA 15 MW turbine located at De Kooy: (a) rain droplet diameter, (b) rain intensity, (c) angular position of the blade and (d) wind speed.

Similarly, f_D(I), f_D(θ) and f_D(V_wind) can be found. By normalizing D, influences of drop-size effects on the absolute lifetime are excluded. This makes the comparison of drop-size effects easier. f_D(ϕ) represents a probability density function. Consequently, $F_D\left(\mathit{\varphi }\right)={\int }_{\mathrm{0}}^{\mathit{\varphi }}{f}_D\left({\mathit{\varphi }}^{\prime }\right)\mathrm{d}{\mathit{\varphi }}^{\prime }$ represents the cumulative distribution function (CDF). The decomposition of the damage into its PDF and CDF is shown for all four independent variables in Fig. 10.

Figure 10a shows the decomposition with respect to the droplet diameter. It is important to note here that the figure shows the damage that is associated with the total water volume comprised by all droplets of a particular diameter. It does not show the damage for a single droplet. The figure shows that when drop-size effects are excluded, droplets of around 1 mm contribute the most toward erosion damage. Half of the total erosion damage is created by droplets of 1.26 mm and below, and 97.0 % of the damage is created by droplets up to a size of 3 mm. The inclusion of drop-size effects causes a shift toward larger droplet diameters. The droplet diameter contributing the most toward erosion damage then becomes 1.67 mm. The probability density function with drop-size effects has a plateau region. Therefore, a wider range of droplets becomes important for erosion. Half of the erosion damage is created by droplets of 2.00 mm and below. Droplets up to 3 mm in diameter create 84.8 % of the erosion damage. Hence, droplets over 3 mm in diameter become significant for erosion when drop-size effects are properly accounted for.

Figure 10b shows how the drop-size effects influence the decomposition of the erosion damage with respect to the rain intensity. Similar to Fig. 10a, inclusion of the drop-size effects shifts damage production to higher rain intensities. Without drop-size effects, 50 % of the total damage is produced by rain intensities of 1.82 mm h⁻¹ and below. With the inclusion of the drop size, this value changes to 2.81 mm h⁻¹. The probability density functions show that the damage contribution is reduced for precipitation events of approximately 2.2 mm h⁻¹ and below, whereas above this value, the damage contribution is increased.

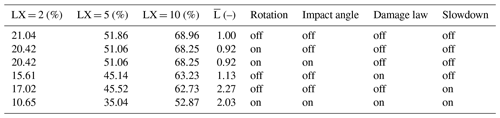
Table 1 Summary showing the influence of the drop-size-dependent effects on the lifetime and percentage time a turbine needs to stop (S-ESM) during precipitation to realize a particular lifetime extension (LX). Normalized lifetime is defined as $\stackrel{\mathrm{‾}}{L}=L/L_{\text{All-off}}$; results are for the De Kooy site.

The decomposition of the damage with respect to the blade's angular position is shown in Fig. 10c. Without any drop-size effects, the damage production is constant for all blade positions, and hence, the damage accumulates linearly toward unity. When drop-size effects are included, one can see that during the upstroke (−90° < θ < 90°; see Fig. 2b), damage production is higher than during the downstroke (90° < θ < 270°). The difference is significant. At θ = 0°, the damage is about 3 times higher than at θ = 180°. Therefore, most erosion damage is created during the upstroke of the blade.

As shown in Fig. 10d, drop-size effects have a negligible influence on the decomposition with respect to the wind speed. With drop-size effects, the variable load region contributes slightly more toward the erosion damage.

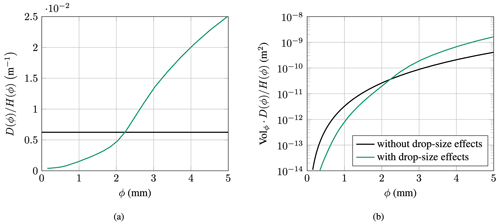
Figure 11 Normalized and absolute erosion damage for a single droplet at varying diameters for the IEA 15 MW turbine located at De Kooy: (a) damage per meter impingement and (b) damage per droplet on area dA.

Previously, in Fig. 10a, the damage associated with all droplets of a particular size was shown. However, it is also possible to compute the damage associated with a single droplet. Firstly, one can calculate the damage per droplet normalized by water mass. This excludes differences in erosion damage due to small and large droplets having different volumes. Secondly, the water volume can be added to obtain the absolute damage for a single water droplet.

The normalized damage for a droplet of a particular diameter is given by

$$\begin{array}{}\text{(41)}& {\displaystyle \frac{D\left(\mathit{\varphi }\right)}{H\left(\mathit{\varphi }\right)}}={\displaystyle \frac{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{\int }_{\mathrm{0}}^{\mathrm{\infty }}{\int }_{\mathrm{0}}^{\mathrm{360}}{\partial }_t{D}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}\mathrm{d}\mathit{\theta }\mathrm{d}{V}_{\text{wind}}\mathrm{d}I}{{\int }_{\mathrm{0}}^{\mathrm{\infty }}{\int }_{\mathrm{0}}^{\mathrm{\infty }}{\int }_{\mathrm{0}}^{\mathrm{360}}{\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}\mathrm{d}\mathit{\theta }\mathrm{d}{V}_{\text{wind}}\mathrm{d}I}}.\end{array}$$

This is equal to the damage that is created per 1 m impingement of droplets of a particular size. Similarly, the absolute damage accounting for differences in water volume is given by

$$\begin{array}{}\text{(42)}& {\text{Vol}}_{\mathit{\varphi }}{\displaystyle \frac{D\left(\mathit{\varphi }\right)}{H\left(\mathit{\varphi }\right)}}={\displaystyle \frac{D\left(\mathit{\varphi }\right)}{n_{\mathit{\varphi }}/\mathrm{dA}}},\end{array}$$

where the relation is used such that $H\left(\mathit{\varphi }\right)=n_{\mathit{\varphi }}{\text{Vol}}_{\mathit{\varphi }}/\mathrm{dA}$, where Vol_ϕ is the volume of a droplet with diameter ϕ. n_ϕ is the number of droplets of a particular diameter and dA is a surface element of the blade; see Appendix A1. Hence, Eq. (42) is the damage created per droplet on a surface area element dA.

The metrics of Eqs. (41) and (42) are shown in Fig. 11. It is important to note that the numerical values of the curves with and without drop-size effects cannot be directly compared. The reason is that drop-size effects also influence the absolute lifetime. This aspect is further discussed in Sect. 3 and, particularly, in Table 1. Hence, only the behavior of the curves is of interest here.

In Fig. 11a, the damage caused by all drop sizes is constant when drop-size-dependent effects are neglected. With drop-size effects, one can see that large droplets produce significantly more damage for the same amount of water. For example, the damage produced by 4 mm droplets is about 14 times higher than that of 1 mm droplets, for equal amounts of water. In Fig. 11b, the absolute damage for a single droplet is given. Including the water volume significantly amplifies the difference in damage production between a small and a large droplet. Without drop-size effects, a 4 mm droplet is, as expected, 64 times more damaging than a droplet of 1 mm in diameter. If drop-size effects are included, this increases to 896 times.

2.4 Synthesis

The analysis presented in this section revealed that the following relevant drop-size-dependent effects are contained within the assumed damage model.

• Rotation of the blade. Larger droplets have a higher terminal velocity. This, averaged over one rotation, leads to more damage due to the non-linear nature of the damage model.

• The slowdown effect. Large droplets have less slowdown than small droplets. Hence, large droplets have a higher impact speed.

• Damage law. In the relevant impact-speed range for current wind turbines, large droplets have a lower allowed impingement.

From these effects, it was concluded that for the same impingement, large rain droplets must be more damaging than small droplets. The drop-size distribution of Eq. (11) is visualized in Fig. 12. It states that rain becomes comprised of larger and larger droplets with increasing rain intensity. Hence, for the same amount of impingement, higher-rain-intensity events should create more erosion damage. The erosion damage per meter impingement of a particular rain intensity is given in Fig. 13. The formula for the damage is analogous to Eq. (41). As before, the damage is not equal for both curves. When no drop-size effects are included, the erosiveness is constant across the rain intensities. It is noteworthy that the value of $D\left(I\right)/H\left(I\right)$ = 0.624 × 10⁻³ m⁻¹ is equal to the one in Fig. 11a. Hence, when drop-size effects are excluded, the normalized damage is invariant with respect to the droplet diameter and rain intensity. As predicted, when the drop-size effects are included, the erosiveness rapidly increases with increasing rain intensity. This corroborates statement three in Sect. 2.2. These findings directly influence the operation of the ESM. This aspect is discussed in the next section.

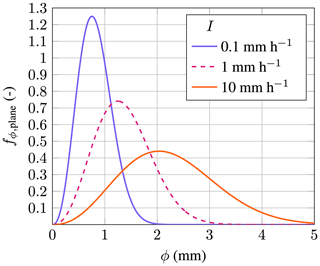
Figure 12 Best's distribution for a plane as a function of droplet diameter in millimeters for different rain intensities; the figure is partly reproduced from Barfknecht and von Terzi (2023).

3 Influence of drop-size-dependent effects on ESM operation

Drop-size effects cause a shift in erosion damage production to higher rain intensities. As a consequence, the viability of the ESM is affected. As Eq. (12) shows, high-rain-intensity events are rare. With this in mind, it might be possible to avoid a sizable portion of the erosion damage, at minimum AEP loss, by operating in the ESM only during these rare but highly damaging events. Such an ESM variant would then increase its economic viability. In this section, first, the significance of the drop-size effects on the general ESM operation is established. Then, the influence of the drop-size effects on two optimal ESM designs is investigated. Some of the concepts used in this section such as the operating regime of the ESM and an optimal ESM strategy, as well as the detailed derivations of the considered ESM variants, are discussed in Appendix B.

Figure 14 is created to understand which rain events are causing damage. The data on the x axis are defined as

$$\begin{array}{}\text{(43)}& \left(\mathrm{1}-F_{\mathrm{I}}\left(I\right)\right)\cdot \mathrm{100}\mathit{\%}=\left(\mathrm{1}-\underset{\mathrm{0}}{\overset{I}{\int }}{f}_{\mathrm{I}}\left(I^{\prime }\right)\mathrm{d}{I}^{\prime }\right)\cdot \mathrm{100}\mathit{\%}.\end{array}$$

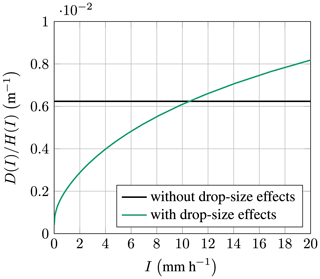
Figure 13 Normalized erosion damage per meter of impingement at various rain intensities for the IEA 15 MW turbine located at De Kooy.

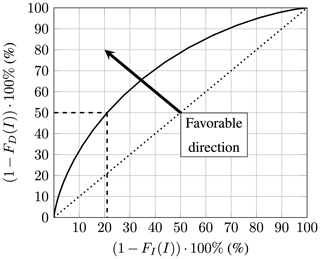
Figure 14 Non-dimensional damage that can be avoided by stopping the turbine (S-ESM) versus the X % of highest intensity rain events (without drop-size effects). The dotted line for reference is for equal contribution.

The graph should be interpreted in the following way:

• x axis – stopping the turbine during the X % highest-rain-intensity events

• y axis – will save Y % of damage.

For example, fully stopping the turbine during the ≈ 21 % highest-rain-intensity events will avoid 50 % of the total erosion damage. In the following, fully stopping the turbine during precipitation will be referred to as STOP-ESM or, in short, S-ESM.

The figure shows that the damage follows a concave curve. For better visualization, a 1:1 line is also given. From an ESM perspective, it would be advantageous if the curve was pulled in the direction of the arrow, i.e., make it more concave. Most damage would then be created during a few heavy rain events during the year.

A series of computations were performed to study the influence of the drop-size effects on the curve from Fig. 14. First, the influence of the four drop-size-dependent effects from Sect. 2.2 is quantified independently. Subsequently, the effects are combined. Three distinct points on the curve were chosen to represent the curve in a convenient and condensed format. They are the 50 %, 80 % and 90 % damage avoidance points. These correspond to a lifetime extension ($\text{LX}=L_{\text{ESM}}/L_{\text{no ESM}}$, L is the incubation time) by factors of 2, 5 and 10. Table 1 shows the corresponding values of Eq. (43) for these three reference points. The first row in the table sets a benchmark with all drop-size-dependent effects deactivated. The four independent simulations are as follows.

1. Rotation. On – V_{circumferential} is calculated according to Eq. (22); off – blade is fixed at θ = 90° thus $V_{\text{circumferential}}=V_{\text{sec}}(\mathrm{1}+a^{\prime })$. Note that the impact angle is set to off; see next point and Table 1.

2. Impact angle. On – cos α_ϕ is calculated with Eq. (22) in Eq. (31); off – cos α_ϕ is calculated with $V_{\text{circumferential}}=V_{\text{sec}}(\mathrm{1}+a^{\prime })$ and, hence, cos α_ϕ=cos α, where α is the angle of attack.

3. Damage law. On – drop-size-dependent damage law given by Eqs. (6)–(8); off – averaged damage law given by Eq. (5).

4. Slowdown. On – V_slowdown is calculated; off – V_slowdown=0.

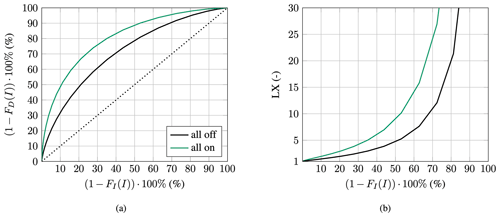
Figure 15 Curves showing the damage avoidance (a) and lifetime extension factor (b) against the X % of heaviest rain events; this is equivalent to operating in an S-ESM.

Without any drop-size effects, the damage model predicts that turning off (S-ESM) the turbine during the 21.04 % heaviest rain events will avoid 50 % of the total erosion damage. Activating the rotation effect decreases this value slightly to 20.42 %. The influence on the absolute lifetime is stronger. Here, the normalized lifetime $\stackrel{\mathrm{‾}}{L}$ is decreased from 1.00 to 0.92. As previously predicted in Sect. 2.2.2, impact angle has no measurable influence on the results. A much more significant impact can be observed from the drop-size-dependent damage law and the slowdown effect. The damage law and slowdown shift the values for the 50 % point to 15.61 % and 17.02 %, respectively. When combined, the 50 % point is shifted to 10.65 %. An even larger influence can be observed for the 80 % point, where the percentages change from 51.86 % to 35.04 %. The All-Off and All-On cases are plotted in Fig. 15. Compared to the all-off curve, the All-On curve has shifted significantly to the upper-left corner of the figure. When looking at the LX, one can see that at 50 % (x axis), the lifetime increases from approximately a factor of 5 to a factor of 9, almost doubling.

It can be concluded that including drop-size effects within the damage model strongly influences the absolute lifetime. Additionally, the damage production is significantly shifted to higher rain intensities. To illustrate this point further, assume a turbine was to follow an ESM strategy of stopping during precipitation events with the aim of reducing erosion damage by 50 %. If the ESM design was based on a damage model without drop-size effects, then it would stop during approximately 21 % of all precipitation events. However, with drop-size-dependent effects adequately taken into account, it would actually only be required to stop during the 10.65 % highest-rain-intensity events. As a consequence, the ESM would overshoot on its intended LX at the cost of increased AEP losses. Therefore, an ESM needs to be based on an accurate prediction from an erosion damage model. Otherwise, it is not possible to objectively determine which conditions are erosive. If the damage model neglects drop-size effects, the ESM strategy will be sub-optimal.

Compared to other strategies, the S-ESM can only provide a minor increase in LX for a particular AEP loss. Methods that gradually adjust the tip speed based on weather conditions perform significantly better. Two options from this group are the V-ESM and VI-ESM. The former regulates the tip speed based on the wind speed V_wind, whereas the latter additionally considers the rain intensity I. For an explanation and derivation of both strategies, see Appendix B2.

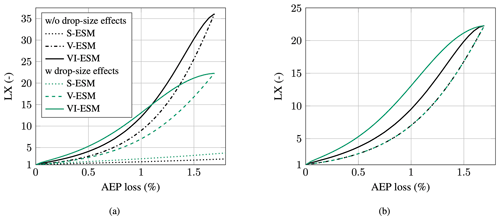
Figure 16 Pareto curves of lifetime extension as a function of the AEP loss (for more information on how to interpret this figure the reader should consult Figs. B1 and B5 and their corresponding explanation in the text) for the IEA 15 MW turbine located at De Kooy: (a) lifetime extension and (b) scaled lifetime extension.

The low performance of the S-ESM in comparison to the V-ESM and VI-ESM becomes apparent when looking at their Pareto fronts in Fig. 16a. A Pareto front represents the maximum LX that can be achieved for a particular AEP loss. In the figure, all curves are normalized with the nominal erosion lifetime in the absence of any ESM. Therefore, all curves start at 0 % AEP loss and at an LX of unity. The S-ESM performs poorly and can only provide a maximum LX of 2.5 for an AEP loss of about 1 %. While the V-ESM and VI-ESM perform much better, there are also striking performance differences between them, where the latter is clearly superior. For further details on the concept of the Pareto front of an ESM, the reader should consult Appendix B1 and especially Fig. B1.

Due to poor performance, the S-ESM represents merely a theoretical strategy. In contrast, the V-ESM and VI-ESM are much more suitable for practical implementation. The question arises of how drop-size effects influence the performance of the VI-ESM. Since it is based on the rain intensity, it should profit from the more accurate relation between damage accumulation and rain intensity. Figure 16a shows that the VI-ESM performance as well is significantly increased when drop-size effects are properly accounted for. This is visible by the spread, i.e., the horizontal distance between the Pareto fronts of the V-ESM and VI-ESM. The ESM strategies with drop-size effects show a much wider spread.

Drop-size effects also influence the prediction of the absolute lifetime. To remove this factor and to be able to better compare the influence of the drop-size effects on the shape of the Pareto fronts, a rescaling operation was performed. For that purpose, the Pareto front of V-ESM without drop-size effects was rescaled so that it became equal to the Pareto front of V-ESM with drop-size effects. The scaling values found were then applied to the Pareto front of the VI-ESM without drop-size effects. For clarification, the rescaling of the VI-ESM was performed with

$$\begin{array}{}\text{(44)}& \begin{array}{rl}L{X}_{\text{VI-ESM,\hspace{0.17em}\hspace{0.17em}rescaled,\hspace{0.17em}\hspace{0.17em}all-off}}=& L{X}_{\text{VI-ESM,\hspace{0.17em}\hspace{0.17em}all-off}}\\ & \times {\displaystyle \frac{L{X}_{\text{V-ESM,\hspace{0.17em}\hspace{0.17em}all-on}}}{L{X}_{\text{V-ESM,\hspace{0.17em}\hspace{0.17em}all-off}}}}.\end{array}\end{array}$$

The result is shown in Fig. 16b. It can be seen that both V-ESM curves become identical. The horizontal spread between V-ESM and VI-ESM approximately doubles when drop-size effects are taken into account. At 1 % AEP loss, the V-ESM has an LX of about 7, while the VI-ESM without drop-size effects has a lifetime extension of 9.5. However, when drop-size effects are properly modeled, the figure reveals that the VI-ESM can actually achieve an LX of 13.1. Therefore, failing to properly account for drop-size effects will make the VI-ESM look significantly worse, potentially indicating that an ESM might not be feasible, while in reality it may well be.

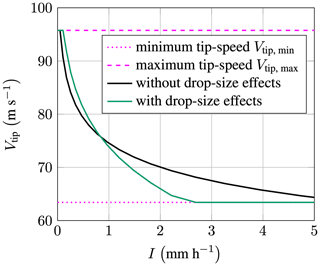
Figure 17 Slice of the tip-speed surface of the VI-ESM mode at 1 % AEP loss as a function of rain intensity; the figure shows a slice analogous to Fig. B4c that intersects the tip-speed control surface at V_wind = 15 m s⁻¹.

Figure 17 shows the influence of the drop-size effects on the VI-ESM's tip-speed surfaces, which is the tip speed as a function of the wind speed and rain intensity, i.e., g(V_wind,I); for reference, see Eq. (B5). The resulting surface for a target AEP loss of 1 % was chosen. Only a slice through the surface at V_wind = 15 m s⁻¹ is shown. As expected, the curve of the ESM without drop-size effects has a higher tip speed at higher rain intensities (≈ 1–5 mm h⁻¹). This is because without drop-size effects in the damage model, the amount of erosion these intensities cause is underpredicted. On the contrary, the curve of the ESM with drop-size effects reduces the tip speed in this region up to the minimum tip speed. As compensation, it retains the maximum tip speed a bit longer at lower rain intensities.

4 Conclusions

In this study, an erosion damage model for wind turbines was developed that is based on the impingement metric. Several drop-size-dependent effects were shown to be included within the proposed model. The importance of these effects was demonstrated for the IEA 15 MW reference wind turbine, a site in the Netherlands and a commercial leading-edge coating. The sensitivity of the ESM design to the drop-size-dependent effects was characterized. The two research questions posed in this study are detailed in the following subsections.

(1) How does the drop size influence the erosivity?

• Four drop-size effects were identified inside the damage model developed. The two dominant effects are the drop-size-dependent damage law from Bech et al. (2022) and the slowdown effect from Barfknecht and von Terzi (2023). It was found that large droplets are significantly more damaging than small droplets, normalized for water volume. It was also found that the exclusion of drop-size effects leads to a severe underestimation in the projected erosion lifetime.

• The higher erosivity of large droplets can be attributed to their higher impact velocity. Additionally, the damage model from Bech et al. (2022) suggests that in the relevant impact-velocity range, the allowed impingement reduces with an increase in droplet diameter.

• The parameter space of leading-edge erosion is affected by drop-size effects. Without such effects, 50 % of damage is created by droplets below 1.26 mm in diameter, whereas with drop-size effects, this value is shifted to 2.00 mm. These effects need to be taken into account when determining the relevant parameters for theoretical and experimental studies in erosion research.

(2) Is a thorough understanding of drop-size-related effects important for the design of the erosion-safe mode?

• Drop-size effects push the damage production to higher rain intensities. It was found that without drop-size effects, 50 % of the erosion damage is caused by ca. 21 % of the highest-intensity rain events. However, with drop-size effects, this value was roughly halved (10.65 %).

• The VI-ESM strategy is highly sensitive to drop-size effects. For the turbine and sample site considered, it was found that the damage model indicated, for 1 % AEP loss, an LX of 9.5 without drop-size effects. However, with the proper modeling of the droplet behavior, it was shown that the actual LX is 13.1.

To conclude, it is indeed very important for the design of the ESM to use a damage model that includes drop-size effects properly. Failing in this respect will make the ESM appear to have worse performance than it actually does, or it will lead to a suboptimal strategy that will suffer from overshoots in the targeted LX at the cost of significantly higher AEP loss than intended.

The damage model used in this study requires a range of parameters and sub-models. These can influence the outcomes of this study. The largest uncertainty concerns the drop-size dependency of the leading-edge material. Currently, to the authors' best knowledge, Bech et al. (2022) published the only study that independently tested a coating for various drop sizes. The importance of the slowdown effect is projected to grow in the future. The slowdown depends on the aerodynamic nose radius R_c and the tip speed. Both are expected to increase as wind turbine blades become larger. For future work, performing a sensitivity study that explores the influence of the parameters and sub-models that describe the considered turbine, site and material is recommended.

Several other findings and conclusions were made as a byproduct of this research. These are included in the appendix. It was shown that for impingement, the damage scales according to $\propto V_{\text{impact}}^{\mathit{\beta }}{V}_{\text{collection}}\approx V_{\text{impact}}^{\mathit{\beta }+\mathrm{1}}$. Additionally, the operational regime of the ESM was defined and a method to find an optimal ESM strategy was proposed. In particular, we conclude the following.

• The VI-ESM is substantially more powerful than the V-ESM. Even without properly modeling drop-size effects, the VI-ESM can provide significantly more life extension for the same AEP loss.

• The drop-size distribution f_ϕ,plane is crucial. The drop-size effects are only relevant because large droplets become more frequent at higher rain intensities. For using the ESM in the field, the drop-size distribution must reflect the actual conditions at the wind turbine site considered.

• The VI-ESM η-contours are not dependent on the rain intensity and wind speed probability density functions.

Appendix A: The impingement collected by a wind turbine blade

This appendix provides a formal derivation for the impingement collected by a blade. Impingement is the damage metric used in this study's damage model. Previous studies have not shown such a derivation, leaving potential ambiguity in how impingement should be computed (López et al., 2023; Visbech et al., 2023). Additional clarification has become necessary due to the introduction of the slowdown effect in leading-edge erosion (Barfknecht and von Terzi, 2023). The first part gives a general derivation of impingement and discusses several evaluation approaches. The second part derives the formula for V_collection.

A1 Derivation of the impingement equation and evaluation approaches

Impingement is the amount of water that is collected by the blade. The concept can be viewed in a more tangible way by considering a bucket mounted to the leading edge of a wind turbine blade. The water inside the bucket after a certain operational time is the impingement. Two different impingement metrics can be defined: H⁽³⁾ and H⁽¹⁾. The former represents the intercepted water volume and the later the intercepted water column. In particular $H^{\left(\mathrm{1}\right)}=H^{\left(\mathrm{3}\right)}/\mathrm{dA}$, where dA is an (infinitesimal) surface element of the blade. We therefore find for the dimensions [H⁽¹⁾]=L and [H⁽³⁾]=L³.

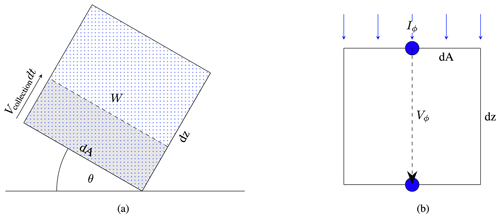
Figure A1 Representation of the flow domain and control volume used to derive H⁽³⁾. (a) Flow domain of air with rain (blue dots); it is oriented at an arbitrary blade angle θ and is swept by a wind turbine blade section dA. The volume swept during dt is indicated in light gray. (b) The control volume for the derivation of W; rain enters at the top of the control volume and subsequently falls through the volume until it reaches the lower boundary.

The general form of impingement for a blade sweeping a flow domain of air that contains rain is

$$\begin{array}{}\text{(A1)}& H^{\left(\mathrm{3}\right)}=\underset{\mathrm{0}}{\overset{T}{\int }}{\displaystyle \frac{\partial H^{\left(\mathrm{3}\right)}}{\partial t}}\mathrm{d}t,\end{array}$$

where t is the time and $\partial H^{\left(\mathrm{3}\right)}/\partial t$ is the volume of water collected per unit of time. From Fig. A1a one can see that

$$\begin{array}{}\text{(A2)}& {\displaystyle \frac{\partial H^{\left(\mathrm{3}\right)}}{\partial t}}=W{V}_{\text{collection}}\mathrm{dA},\end{array}$$

where V_collection is the speed at which the flow domain is swept by the blade. dA is an (infinitesimal) surface element on the leading edge, and W is the volume of water (rain) contained per volume of air. W can also be named the water volume fraction. By definition,

$$\begin{array}{}\text{(A3)}& W={\displaystyle \frac{\mathrm{d}{\text{Vol}}_{\text{water}}}{\mathrm{d}{\text{Vol}}_{\text{air}}}}.\end{array}$$

To find W, we consider Fig. A1b. The volume of air is given by

$$\begin{array}{}\text{(A4)}& \mathrm{d}{\text{Vol}}_{\text{air}}=\mathrm{dA}\mathrm{d}z=\mathrm{d}x\mathrm{d}y\mathrm{d}z.\end{array}$$

The volume of water contained inside the control volume can be calculated by first considering the control volume to be empty. Water enters the volume via its top face. The time is recorded when the water reaches the lower boundary. At that time, the fluxes from the top and bottom face cancel each other out. Hence,

$$\begin{array}{}\text{(A5)}& \mathrm{d}{\text{Vol}}_{\text{water}}=I\mathrm{dA}\mathrm{d}{t}_{\text{fall\hspace{0.17em}\hspace{0.17em}through}}.\end{array}$$

I is the rain intensity, or interpreted differently, it is the normalized surface flux of water (volume) in the dimension [LT⁻¹]. dt_{fall  through} is the fall-through time of the rain. From Fig. A1b,

$$\begin{array}{}\text{(A6)}& \mathrm{d}{t}_{\mathit{\varphi },\text{fall\hspace{0.17em}\hspace{0.17em}through}}={\displaystyle \frac{\mathrm{d}z}{V_{\mathit{\varphi }}}}.\end{array}$$

V_ϕ is the terminal velocity of the rain. However, as shown in Fig. 3, the terminal velocity is a function of the droplet diameter and is thus not universal. Hence, W is dependent on ϕ. We need to find W_ϕ, the water volume fraction as a function of the droplet diameter. For that, we consider the rain intensity of every droplet diameter, which is

$$\begin{array}{}\text{(A7)}& I_{\mathit{\varphi }}=f_{\mathit{\varphi },\text{plane}}I.\end{array}$$

f_ϕ,plane is the distribution of water (mass) through a plane as a function of the drop diameter; see Eq. (11). Note that ${\int }_{\mathrm{0}}^{\mathrm{\infty }}{f}_{\mathit{\varphi },\text{plane}}\mathrm{d}\mathit{\varphi }=\mathrm{1}$. By combining Eqs. (A3)–(A7), we obtain

$$\begin{array}{}\text{(A8)}& W_{\mathit{\varphi }}={\displaystyle \frac{f_{\mathit{\varphi },\text{plane}}I}{V_{\mathit{\varphi }}}}.\end{array}$$

Inserting this into Eq. (A2) yields

$$\begin{array}{}\text{(A9)}& {\displaystyle \frac{\partial H_{\mathit{\varphi }}^{\left(\mathrm{3}\right)}}{\partial t}}=W_{\mathit{\varphi }}{V}_{\text{collection}}\mathrm{dA}={\displaystyle \frac{f_{\mathit{\varphi },\text{plane}}I}{V_{\mathit{\varphi }}}}{V}_{\text{collection}}\mathrm{dA}.\end{array}$$

Later it will be shown that V_collection is also a function of the droplet diameter. By integrating over the droplet diameter, we obtain

$$\begin{array}{}\text{(A10)}& {\partial }_t{H}^{\left(\mathrm{3}\right)}=\mathrm{dA}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{f_{\mathit{\varphi },\text{plane}}I}{V_{\mathit{\varphi }}}}{V}_{\text{collection}}\mathrm{d}\mathit{\varphi },\end{array}$$

or

$$\begin{array}{}\text{(A11)}& {\partial }_t{H}^{\left(\mathrm{1}\right)}=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{f_{\mathit{\varphi },\text{plane}}I}{V_{\mathit{\varphi }}}}{V}_{\text{collection}}\mathrm{d}\mathit{\varphi }.\end{array}$$

For conciseness, we define $\partial H/\partial t={\partial }_{t}H$. Finally, H⁽¹⁾ and analogously H⁽³⁾ can be obtained by

$$\begin{array}{}\text{(A12)}& H^{\left(\mathrm{1}\right)}=\underset{\mathrm{0}}{\overset{T}{\int }}{\partial }_t{H}^{\left(\mathrm{1}\right)}\mathrm{d}t,\end{array}$$

where T is the time during which rain is collected. The full version of Eq. (A11) is obtained by substituting V_collection. It is determined in the next section. For the definition of V_collection, see Eq. (21). The equation becomes

$$\begin{array}{}\text{(A13)}& \begin{array}{rl}{\partial }_t{H}^{\left(\mathrm{1}\right)}(I,V_{\text{wind}},\mathit{\theta })=& \underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{f_{\mathit{\varphi },\text{plane}}I}{V_{\mathit{\varphi }}}}\left(V_{\text{sec}}\right(\mathrm{1}+a^{\prime })\\ & \times \cos \mathit{\phi }+V_{\mathit{\varphi }}\cos \mathit{\theta }\cos \mathit{\phi }\\ & +V_{\text{wind}}(\mathrm{1}-a)\sin \mathit{\phi })\mathrm{d}\mathit{\varphi },\end{array}\end{array}$$

where the independent variables that change during turbine operation are given in parenthesis. From this equation, simplified versions can be derived. Noting that V_sec is significantly larger than all other summands and cos φ≈1, one obtains

$$\begin{array}{}\text{(A14)}& \begin{array}{rl}{\partial }_t{H}^{\left(\mathrm{1}\right)}\approx V_{\text{sec}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{f_{\mathit{\varphi },\text{plane}}I}{V_{\mathit{\varphi }}}}\mathrm{d}\mathit{\varphi }& =V_{\text{sec}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}\mathrm{d}\mathit{\varphi }\\ & =W{V}_{\text{sec}}.\end{array}\end{array}$$

For V_wind=0, V_sec=0, φ = 0° and a blade position of θ = 0°, Eq. (A13) reduces to

$$\begin{array}{}\text{(A15)}& {\partial }_t{H}^{\left(\mathrm{1}\right)}=I\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{\mathit{\varphi },\text{plane}}\mathrm{d}\mathit{\varphi }=I,\end{array}$$

which is simply the rate of rain falling through an imaginary plane, or expressed differently, the rate of rain caught by a rain gauge located on the ground under ideal conditions.

Equation A12 requires continuous time integration over ∂_tH⁽¹⁾. However, it is too difficult or potentially even impossible to calculate this definite integral. A solution approach is to discretize this equation by

$$\begin{array}{}\text{(A16)}& H^{\left(\mathrm{1}\right)}=\sum _{i=\mathrm{1}}^N{\left({\partial }_t{H}^{\left(\mathrm{1}\right)}\left(I\right(t_i),V_{\text{wind}}(t_i),\mathit{\theta }(t_i\left)\right)\right)}_i\mathrm{\Delta }{T}_i,\end{array}$$

where ΔT_i is a fixed time interval. However, for studies that do not use discrete input data (like this one), it is more convenient to express the time integral probabilistically using probability density functions. According to the law of large numbers, the mean converges to the expected value, i.e.,

$$\begin{array}{}\text{(A17)}& {\displaystyle \frac{\mathrm{1}}{T}}\underset{\mathrm{0}}{\overset{T}{\int }}y\left(x\right(t\left)\right)\mathrm{d}t=\underset{x_L}{\overset{x_U}{\int }}y\left(x\right)f_x\mathrm{d}x,\end{array}$$

where y is a function. x(t) is variable depending on t, for example, the rain intensity. f_x is the PDF of x so that ${\int }_{x_L}^{x_U}{f}_x\mathrm{d}x=\mathrm{1}$. Subscripts U and L indicate the upper and lower bounds of integration. With this, one can rewrite Eq. (A12) as

$$\begin{array}{ll}\text{(A18)}& {\displaystyle }{H}^{\left(\mathrm{1}\right)}& {\displaystyle }=\underset{\mathrm{0}}{\overset{T}{\int }}{\partial }_t{H}^{\left(\mathrm{1}\right)}\left(x_{\mathrm{1}}\right(t),\mathrm{\dots },x_n(t\left)\right)\mathrm{d}t{\displaystyle }& {\displaystyle }=T\underset{x_{{\mathrm{1}}_L}}{\overset{x_{{\mathrm{1}}_U}}{\int }}\mathrm{\dots }\underset{x_{N_L}}{\overset{x_{N_U}}{\int }}{\partial }_t{H}^{\left(\mathrm{1}\right)}(x_{\mathrm{1}},\mathrm{\dots },x_n)f_{x_{\mathrm{1}}}\mathrm{\dots }{f}_{x_N}\mathrm{d}{x}_{\mathrm{1}}\mathrm{\dots }\mathrm{d}{x}_N\\ {\displaystyle }& {\displaystyle }=T\underset{x_{{\mathrm{1}}_L}}{\overset{x_{{\mathrm{1}}_U}}{\int }}\mathrm{\dots }\underset{x_{N_L}}{\overset{x_{N_U}}{\int }}{\partial }_t{H}_{x_{\mathrm{1}},..,x_N}^{\left(\mathrm{1}\right)}(x_{\mathrm{1}},\mathrm{\dots },x_n)\mathrm{d}{x}_{\mathrm{1}}\mathrm{\dots }\mathrm{d}{x}_N.\end{array}$$

Note that ${\partial }_t{H}^{\left(\mathrm{1}\right)}\left(x_{\mathrm{1}}\right(t),\mathrm{\dots },x_n(t\left)\right)\ne {\partial }_t{H}^{\left(\mathrm{1}\right)}(x_{\mathrm{1}},\mathrm{\dots },x_n)$. Additionally, the definition

$$\begin{array}{}\text{(A19)}& {\partial }_t{H}_x^{\left(\mathrm{1}\right)}\left(x\right)={\partial }_t{H}^{\left(\mathrm{1}\right)}\left(x\right)f_x\end{array}$$

is used. In this study, four integrals over the variables I, V_wind, θ and ϕ need to be evaluated. However, the integral over ϕ is not directly visible in Eq. (A18) but is somewhat hidden in Eq. (A13). Additionally, both equations have a similar form, since they both integrate over at least one PDF. To improve readability, we define, similar to Eq. (A9),

$$\begin{array}{}\text{(A20)}& {\partial }_t{H}_{\mathit{\varphi }}^{\left(\mathrm{1}\right)}\left(\mathit{\varphi }\right)={\partial }_t{H}^{\left(\mathrm{1}\right)}\left(\mathit{\varphi }\right)f_{\mathit{\varphi },\text{plane}},\end{array}$$

with

$$\begin{array}{}\text{(A21)}& {\partial }_t{H}^{\left(\mathrm{1}\right)}\left(\mathit{\varphi }\right)={\displaystyle \frac{I}{V_{\mathit{\varphi }}}}{V}_{\text{collection}}.\end{array}$$

Notice that ${\partial }_t{H}^{\left(\mathrm{1}\right)}\ne {\partial }_t{H}^{\left(\mathrm{1}\right)}\left(\mathit{\varphi }\right)$. By transferring Eq. (A12) into the probabilistic form, one obtains the equation for impingement used in this study. It reads

$$\begin{array}{}\text{(A22)}& {\displaystyle }\begin{array}{rl}{H}^{\left(\mathrm{1}\right)}=& T\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}\mathit{°}}{\overset{\mathrm{360}\mathit{°}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\partial }_t{H}_{\mathrm{I},V_{\text{wind}},\mathit{\theta },\mathit{\varphi }}(I,V_{\text{wind}},\mathit{\theta },\mathit{\varphi })\\ & \times \mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }\mathrm{d}{V}_{\text{wind}}\mathrm{d}I\end{array}\text{(A23)}& {\displaystyle }\begin{array}{rl}=& T\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}\mathit{°}}{\overset{\mathrm{360}\mathit{°}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\partial }_{t}H(I,V_{\text{wind}},\mathit{\theta },\mathit{\varphi })f_{\mathrm{I}}{f}_{V_{\text{wind}}}\\ & \times f_{\mathit{\theta }}{f}_{\mathit{\varphi },\text{plane}}\mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }\mathrm{d}{V}_{\text{wind}}\mathrm{d}I.\end{array}\end{array}$$

Substituting Eqs. (A21) and (21) leads to

$$\begin{array}{}\text{(A24)}& {\displaystyle }\begin{array}{rl}{H}^{\left(\mathrm{1}\right)}=& T\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}\mathit{°}}{\overset{\mathrm{360}\mathit{°}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{I}{V_{\mathit{\varphi }}}}\left(V_{\text{sec}}\right(\mathrm{1}+a^{\prime })\cos \mathit{\phi }\\ & +V_{\mathit{\varphi }}\cos \mathit{\theta }\cos \mathit{\phi }\end{array}\text{(A25)}& {\displaystyle }\begin{array}{rl}& +V_{\text{wind}}(\mathrm{1}-a)\sin \mathit{\phi })f_{\mathrm{I}}{f}_{V_{\text{wind}}}{f}_{\mathit{\theta }}{f}_{\mathit{\varphi },\text{plane}}\\ & \times \mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }\mathrm{d}{V}_{\text{wind}}\mathrm{d}I.\end{array}\end{array}$$

This equation is similar to the Palmgren–Miner damage rule from Eq. (1). In the main body of this study, the superscript is omitted. For all practical purposes, the integrals, once again, need to be evaluated numerically, for example with a simple trapezoidal rule.

When computing the impingement directly from time-dependent meteorological data is required, it might be more convenient to formulate H⁽¹⁾ in a hybrid continuous–discrete form. The rain intensity I and the wind speed V_wind are usually readily available as discrete meteorological data sets. Hence, I and V_wind are considered to be discrete and constant over one time interval ΔT_i. However, for θ and for ϕ, time-dependent data sets are usually not available. For example, it is unlikely that discrete measurements are taken multiple times during one blade rotation. Hence, they should be considered continuous and instead described by their respective probability density functions. As a result, one obtains

$$\begin{array}{}\text{(A26)}& \begin{array}{rl}{H}^{\left(\mathrm{1}\right)}=& \sum _{i=\mathrm{1}}^N{\left(\underset{\mathrm{0}\mathit{°}}{\overset{\mathrm{360}\mathit{°}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\partial }_t{H}_{\mathit{\theta },\mathit{\varphi }}^{\left(\mathrm{1}\right)}\left(I\right(t_i),V_{\text{wind}}(t_i),\mathit{\theta },\mathit{\varphi })\mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }\right)}_i\\ & \times \mathrm{\Delta }{T}_i.\end{array}\end{array}$$

A2 Determination of V_collection

In this section V_collection is determined, which is slightly different from V_impact. The correct determination is important since any error linearly propagates into the accumulated impingement.

Figure A2 Control volume of air containing rain with a blade section oriented at an arbitrary blade angle θ. (a) The control volume fixed in the air is swept by a wind turbine blade section dA; the volume swept during dt is indicated in light gray. (b) The control volume mapped to the reference frame of the blade; the boundary D has become the leading edge of the blade.

Figure A2a shows a control volume that is fixed in space (air) and contains rain. The volume is swept by a blade section with area dA and speed V_sec⋅n_LE. It is aligned with the blade's leading edge in such a way that n_LE=u, where dU=udA. F is the flux vector across the control volume's boundaries. The flux describes the rain that enters and leaves the control volume. It is more convenient to map the problem into the reference frame of the blade by defining the adjusted fluxes ${\mathit{F}}_U^{\prime }$ and ${\mathit{F}}_D^{\prime }$, yielding Fig. A2b.

For the mapped problem, one can write the continuity equation of the control volume as

$$\begin{array}{}\text{(A27)}& {\displaystyle \frac{\partial m}{\partial t}}=\underset{S}{\iint }\mathit{F}\cdot \mathrm{d}\mathit{S},\end{array}$$

where m is the mass of water inside the control volume, and S is the surface vector of the control volume. $\partial m/\partial t$ is the net rate of change of the mass inside the control volume. ${\iint }_S\mathit{F}\cdot \mathrm{d}\mathit{S}$ is the mass entering or leaving the control volume due to the velocity of the rain field.

The surface integral over the boundary S is evaluated by integrating over all four sides separately, that is

$$\begin{array}{}\text{(A28)}& \begin{array}{rl}\underset{S}{\iint }\mathit{F}\cdot \mathrm{d}\mathit{S}=& \underset{R}{\iint }{\mathit{F}}_R\cdot \mathrm{d}\mathit{R}+\underset{L}{\iint }{\mathit{F}}_L\cdot \mathrm{d}\mathit{L}\\ & +\underset{U}{\iint }{\mathit{F}}_U^{\prime }\cdot \mathrm{d}\mathit{U}+\underset{D}{\iint }{\mathit{F}}_D^{\prime }\cdot \mathrm{d}\mathit{D}.\end{array}\end{array}$$

It is assumed that for the length scale of the control volume, the rain field is constant; this implies that ${\mathit{F}}_R={\mathit{F}}_L=\text{const}$. The fluxes of the left and right faces are, therefore, equal in magnitude and direction. The surface normals are, however, opposite in sign; hence,

$$\begin{array}{}\text{(A29)}& \mathrm{0}=\underset{R}{\iint }{\mathit{F}}_R\cdot \mathrm{d}\mathit{R}+\underset{L}{\iint }{\mathit{F}}_L\cdot \mathrm{d}\mathit{L}.\end{array}$$

Additionally, the bottom boundary is aligned and coincidental with the blade's leading edge, so that $\mathit{d}=-{\mathit{n}}_{\text{LE}}$. Thus, the boundary D can be considered the blade's leading edge. It follows that D is impermeable,

$$\begin{array}{}\text{(A30)}& \underset{D}{\iint }{\mathit{F}}_D^{\prime }\cdot \mathrm{d}\mathit{D}=\mathrm{0}.\end{array}$$

The surface integral becomes

$$\begin{array}{}\text{(A31)}& \underset{S}{\iint }\mathit{F}\cdot \mathrm{d}\mathit{S}=\underset{U}{\iint }{\mathit{F}}_U^{\prime }\cdot \mathrm{d}\mathit{U}.\end{array}$$

Therefore, the net rate of change of mass inside the control volume is

$$\begin{array}{}\text{(A32)}& {\displaystyle \frac{\partial m}{\partial t}}=\underset{U}{\iint }{\mathit{F}}_U^{\prime }\cdot \mathrm{d}\mathit{U},\end{array}$$

which can also be interpreted as the rate of mass that is intercepted by the blade. By assuming incompressibility and thus dividing by the density of water ρ, assuming that ${\mathit{F}}_U^{\prime }$ is constant over the boundary patch and dividing by the surface area $\left|\mathit{U}\right|$, one obtains

$$\begin{array}{}\text{(A33)}& {\partial }_t{H}^{\left(\mathrm{1}\right)}={\displaystyle \frac{\mathrm{1}}{\mathit{\rho }\left|\mathit{U}\right|}}\underset{U}{\iint }{\mathit{F}}_U^{\prime }\cdot \mathrm{d}\mathit{U}.\end{array}$$

Due to the transformation of the problem, the modified surface flux is

$$\begin{array}{}\text{(A34)}& {\mathit{F}}_U^{\prime }\cdot \mathrm{d}\mathit{U}={\mathit{F}}_U\cdot \mathrm{d}\mathit{U}-{\mathit{F}}_{\text{sec}}\cdot \mathrm{d}\mathit{A},\end{array}$$

with

$$\begin{array}{}\text{(A35)}& {\mathit{F}}_U\cdot \mathrm{d}\mathit{U}=-\mathit{\rho }\left(\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}{\mathit{V}}_{\text{water}}\mathrm{d}\mathit{\varphi }\right)\cdot \mathrm{d}\mathit{U}\end{array}$$

and

$$\begin{array}{}\text{(A36)}& {\mathit{F}}_{\text{sec}}\cdot \mathrm{d}\mathit{A}=-\mathit{\rho }\left(\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}\mathrm{d}\mathit{\varphi }\right){\mathit{V}}_{\text{sec}}\cdot {\mathit{n}}_{\text{LE}}\mathrm{dA}.\end{array}$$

The minus signs are required so that mass entering the control volume is positive. Combining Eqs. (A33–A36) and using $\mathrm{d}\mathit{U}=\mathrm{dA}\mathit{u}=\mathrm{dA}{\mathit{n}}_{\text{LE}}$ yield

$$\begin{array}{}\text{(A37)}& {\displaystyle }\begin{array}{rl}{\partial }_t{H}^{\left(\mathrm{1}\right)}=& -\left(\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}{\mathit{V}}_{\text{water}}\mathrm{d}\mathit{\varphi }\right)\cdot {\mathit{n}}_{\text{LE}}\\ & +\left(\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}\mathrm{d}\mathit{\varphi }\right){\mathit{V}}_{\text{sec}}\cdot {\mathit{n}}_{\text{LE}}\end{array}\text{(A38)}& {\displaystyle }=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}\left({\mathit{V}}_{\text{sec}}-{\mathit{V}}_{\text{water}}\right)\cdot {\mathit{n}}_{\text{LE}}\mathrm{d}\mathit{\varphi }.\end{array}$$

V_sec is given by Eq. (16). V_water can be determined using Fig. 2, which yields

$$\begin{array}{}\text{(A39)}& {\displaystyle }{\mathit{V}}_{\text{water}}\cdot {\mathit{n}}_{\text{LE}}=\left[\begin{array}{c}-\sin \mathit{\theta }{V}_{\text{sec}}{a}^{\prime }\\ -\cos \mathit{\theta }{V}_{\text{sec}}{a}^{\prime }-V_{\mathit{\varphi }}\\ -V_{\text{wind}}(\mathrm{1}-a)\end{array}\right]\cdot \left[\begin{array}{c}\sin \mathit{\theta }\cos \mathit{\phi }\\ \cos \mathit{\theta }\cos \mathit{\phi }\\ \sin \mathit{\phi }\end{array}\right]\text{(A40)}& {\displaystyle }\begin{array}{rl}=& -(V_{\text{sec}}{a}^{\prime }\cos \mathit{\phi }+V_{\mathit{\varphi }}\cos \mathit{\theta }\cos \mathit{\phi }\\ & +V_{\text{wind}}(\mathrm{1}-a)\sin \mathit{\phi }).\end{array}\end{array}$$

Here, it is assumed that the rain droplets are advected with the radial and axial induction factor, the wind speed, and the terminal velocity. Inserting these into Eq. (A38) gives

$$\begin{array}{}\text{(A41)}& \begin{array}{rl}{\partial }_t{H}^{\left(\mathrm{1}\right)}=& \underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}(V_{\text{sec}}\cos \mathit{\phi }+V_{\text{sec}}{a}^{\prime }\cos \mathit{\phi }\\ & +V_{\mathit{\varphi }}\cos \mathit{\theta }\cos \mathit{\phi }+V_{\text{wind}}(\mathrm{1}-a)\sin \mathit{\phi })\mathrm{d}\mathit{\varphi }\mathrm{dA}.\end{array}\end{array}$$

Comparing with Eq. (A11), one obtains

$$\begin{array}{}\text{(A42)}& {\partial }_t{H}^{\left(\mathrm{1}\right)}=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_{\mathit{\varphi }}{V}_{\text{collection}}\mathrm{d}\mathit{\varphi },\end{array}$$

with

$$\begin{array}{}\text{(A43)}& \begin{array}{rl}{V}_{\text{collection}}=& V_{\text{sec}}(\mathrm{1}+a^{\prime })\cos \mathit{\phi }+V_{\mathit{\varphi }}\cos \mathit{\theta }\cos \mathit{\phi }\\ & +V_{\text{wind}}(\mathrm{1}-a)\sin \mathit{\phi }.\end{array}\end{array}$$

In comparison to V_impact, V_collection does not contain the slowdown velocity. It is possible to define $V_{\text{collection}}^{\prime }=V_{\text{impact}}$. However, in that case, W_ϕ needs to be corrected. The slowdown is a local phenomenon that occurs in the proximity of the leading edge on the length scale of the aerodynamic nose radius R_c. It reduces the local velocity of the rain droplets but, at the same time, increases the droplet concentration per volume of air. When both factors are accounted for, the flux remains unchanged. The correction for the case $V_{\text{collection}}^{\prime }=V_{\text{impact}}$ is

$$\begin{array}{}\text{(A44)}& W_{\mathit{\varphi }}^{\prime }={\displaystyle \frac{V_{\text{collection}}}{V_{\text{collection}}-V_{\text{slowdown}}\cos {\mathit{\alpha }}_{\mathit{\varphi }}}}.\end{array}$$

The conclusion is, therefore, that the slowdown effect decreases the impact speed but does not influence the impingement accumulation rate.

Appendix B: Definition of the ESM operational regime and method of finding an optimal ESM strategy

This appendix aims to develop some of the concepts pertaining to the ESM used in Sect. 3. In Appendix B1, the operational regime of the ESM is defined. Appendix B2 provides a semi-analytical approach for finding an optimal ESM strategy.

B1 Operational regime of the ESM

For a practical ESM design, it is not desirable to fully stop the turbine (S-ESM), as the erosion damage savings come at a large AEP penalty. This was shown in Fig. 16a. With the high value of β in mind, a small reduction in the tip speed can already greatly increase the erosion lifetime of the blade, while maintaining a decent amount of power production. Hence, a practical ESM strategy will attempt to mitigate erosion by only slightly but sufficiently reducing the tip speed of a turbine. To this end, it is useful to first understand the operational regime of the ESM before a good strategy can be chosen.

Figure B1 Operational regime of the ESM spanned by the AEP loss and the lifetime extension.

The concept of the ESM can be visualized in an {AEP loss, lifetime extension (LX)} diagram. By reducing the tip speed during precipitation events, a turbine operating in an ESM trades AEP for an extension of its lifetime; i.e., the AEP decreases while the erosion lifetime increases. The regime in which this trade takes place is visualized in Fig. B1. In this figure, points A, B, C and D and their connecting curves form an operational regime. The turbine can only operate within this regime. Point A represents a turbine during normal operation. This means no ESM is utilized during precipitation events. Hence, the turbine experiences no AEP loss (a potential performance loss due to erosion is not considered here), and as a result, the normalized lifetime is unity. The turbine operates at point B when it spins at its minimum rotational speed (5 rpm for the IEA 15 MW reference turbine) during all precipitation events. It is important to note that point B implies that there is perfect knowledge of the incoming precipitation. Additionally, the turbine must also be able to react infinitely fast to changing precipitation conditions. The region is closed by two highly undesirable operating points. Point C represents the operation at the minimum turbine speed at all times, including dry (no rain) conditions. As with point B, point C offers the highest LX. However, this comes at the cost of very high AEP losses because the turbine's speed is permanently reduced, effectively de-rating the turbine. The turbine operates at point D when the wind turbine's speed is reduced to its minimum during dry events only but keeps its nominal speed during precipitation events. Here, no increase in lifetime is achieved. However, a large reduction in AEP is realized, albeit somewhat lower than for point C.

Points A, B, C and D can also be interpreted with respect to the quality of the weather forecast. Point B is realized with a perfect forecast. Point C represents a forecast that indicates precipitation at all times. Point D represents a perfectly inverted forecast, i.e., a forecast that indicates no rain when it actually rains and indicates rain when it is actually dry. Point A can be interpreted as a turbine that is controlled by a weather forecast that never indicates precipitation.

It is straightforward to see that the best ESM is realized when operating on the curve from point A to B, called $\stackrel{\mathrm{‾}}{\text{AB}}$. It represents the Pareto front of an ESM strategy under the assumption of perfect rain knowledge and instantaneous turbine control. The front represents the highest-possible lifetime extension for a minimum of AEP loss. In practice, neither perfect knowledge of precipitation nor instantaneous turbine control can be achieved. Any practical ESM implementation aims to operate as closely as possible to the Pareto front under the practical limitations. The ESM becomes more viable, i.e., more lifetime for a lower AEP loss, if a new Pareto front can be found that is shifted in the direction of the arrow in Fig. B1. The concept is similar to Fig. 14 and similar conclusions hold.

B2 Method for designing an optimal ESM control strategy

This section describes a semi-analytical approach that can be used to find ESM control strategies that lead to optimal Pareto fronts (see Fig. B1). The ESM strategies that have been presented in the literature were, up to now, heuristic (Barfknecht et al., 2022; Bech et al., 2018). Finding the optimal strategy has not yet been described in the literature. Additionally, using the optimal strategy for investigating the drop-size effects, ambiguity in the results concerning the goodness of the Pareto front is eliminated. The approach presented here is straightforward to implement and computationally light, requiring only a few seconds of wall-clock time to compute.

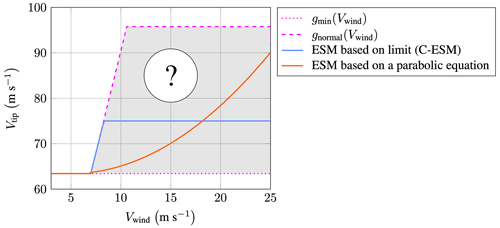
Figure B2 Operational tip-speed regime of the IEA 15 MW turbine as a function of the instantaneous wind speed.

An ESM strategy is a function determining how the turbine operates under precipitation conditions with the aim to maximize lifetime, i.e., to minimize the rain erosion damage, and to minimize AEP loss. Understanding that every ESM strategy leads to a unique Pareto front is important. Hence, some strategies are more optimal than others. At the core is a function that relates the turbine's tip speed to environmental variables. For example,

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}g(V_{\text{wind}},I,\mathrm{\dots })=& \mathit{\left\{}{g}_{\text{min}}\right(V_{\text{wind}})\le V_{\text{tip}}\le g_{\text{normal}}\\ & \times \left(V_{\text{wind}}\right)\text{for all}(V_{\text{wind}},I,\mathrm{\dots })\mathit{\}},\end{array}\end{array}$$

where g_min(V_wind)=V_{tip,  min} is the minimum tip speed, and g_normal(V_wind) is the normal piecewise-linear control function of the turbine. Both are shown in Fig. B2 and span an operational regime colored in gray. An ESM strategy is a curve in this regime. Theoretically, a turbine could spin over the entire wind speed range at the maximum tip speed. However, it will be shown in the following that this is not desirable.

Two straightforward ESM strategies can be derived called the C-ESM and S-ESM. The C-ESM defines a constant upper threshold C to the tip speed and applies this threshold to the normal control curve when precipitation occurs. That is,

$$\begin{array}{}\text{(B2)}& \text{C-ESM}=\left\{\begin{array}{ll}{g}_{\text{normal}}\left(V_{\text{wind}}\right)& \text{if }I=\mathrm{0},\\ min\left(g_{\text{normal}}\right(V_{\text{wind}}),C)& \text{if }I>\mathrm{0}.\end{array}\right.\end{array}$$

The S-ESM reduces the tip speed of the turbine to zero (i.e., stopping it) when the rain intensity exceeds a particular threshold I_th. That is,

$$\begin{array}{}\text{(B3)}& \text{S-ESM}=\left\{\begin{array}{ll}{g}_{\text{normal}}\left(V_{\text{wind}}\right)& \text{if }I\le I_{\text{th}},\\ \mathrm{0}& \text{if }I>I_{\text{th}}.\end{array}\right.\end{array}$$

These methods are heuristic and, in general, do not represent an optimal ESM strategy. Optimal is defined as the curve that provides the maximum lifetime extension for the minimum AEP loss for a particular set of independent environmental variables (V_wind, I, …). For example, the C-ESM is an optimal strategy only when either C=V_{tip, min} or C=V_{tip, max}.

The V-ESM, which only considers the wind speed, is the first strategy that creates an entire optimal Pareto front. It is defined as

$$\begin{array}{}\text{(B4)}& \text{V-ESM}=\left\{\begin{array}{ll}{g}_{\text{normal}}\left(V_{\text{wind}}\right)& \text{if }I=\mathrm{0},\\ g_{\text{opt}}\left(V_{\text{wind}}\right)& \text{if }I>\mathrm{0},\end{array}\right.\end{array}$$

where g_opt is the curve that leads to an optimal strategy. The VI-ESM represents a more advanced strategy that also includes the rain intensity I as another environmental input. The VI-ESM is defined as

$$\begin{array}{}\text{(B5)}& \mathrm{\text{VI-ESM}}=\left\{\begin{array}{ll}{g}_{\text{opt}}(V_{\text{wind}},\mathrm{0})=g_{\text{normal}}\left(V_{\text{wind}}\right)& \text{if }I=\mathrm{0},\\ g_{\text{opt}}(V_{\text{wind}},I)& \text{if }I>\mathrm{0}.\end{array}\right.\end{array}$$

That is, when I=0, the strategy follows the normal tip-speed control curve. If other environmental conditions were to significantly promote erosion, like ambient temperature, UV radiation, etc., then more advanced strategies could be considered.

The question is how to find the optimal curve g_opt within the operational regime. One could heuristically guess a function leading to a strategy such as the C-ESM, which is shown as the blue curve in Fig. B2. Alternatively, one could consider any other arbitrary function, such as the parabolic curve depicted in orange. Subsequently, the coefficients of these functions could be optimized. However, no function that is guessed is guaranteed to lead to the optimal strategy. It is possible to use high-order polynomials. For a sufficiently high order, these could approximate the optimal function closely. However, optimizing for many coefficients is a non-trivial task, especially when g is of a high order and a function of many environmental variables.

Here, it is argued that an ESM strategy is optimal inside the region spanned by g_min(V_wind) and g_normal(V_wind) when

$$\begin{array}{}\text{(B6)}& \begin{array}{rl}{g}_{\text{opt}}=& \mathit{\left\{}g\right(V_{\text{wind}},I,\mathrm{\dots })\\ & \text{ subject\hspace{0.17em}\hspace{0.17em}to\hspace{0.17em}\hspace{0.17em}minimize }\left(\right|\mathit{\eta }\left(g\right(V_{\text{wind}},I,\mathrm{\dots }\left)\right)-K\left|\right)\\ & \text{ for\hspace{0.17em}\hspace{0.17em}all }(V_{\text{wind}},I,\mathrm{\dots })\mathit{\}},\end{array}\end{array}$$

where

$$\begin{array}{}\text{(B7)}& \mathit{\eta }\left(g\right(V_{\text{wind}},I,\mathrm{\dots }\left)\right)={\displaystyle \frac{\frac{\partial P}{\partial V_{\text{tip}}}}{\frac{\partial \left({\partial }_{t}D\right)}{\partial V_{\text{tip}}}}}={\displaystyle \frac{\partial P}{\partial \left({\partial }_{t}D\right)}}.\end{array}$$

$P\left(g\right(V_{\text{wind}},I,\mathrm{\dots }\left)\right)$, abbreviated as P, is the (instantaneous) turbine power, and ${\partial }_{t}D\left(g\right(V_{\text{wind}},I,\mathrm{\dots }\left)\right)$, abbreviated as ∂_tD, is the damage accumulation rate. The choice of the variable K determines an operational tuple of {AEP loss, LX} on the Pareto front. By considering all possible values of K, the entire Pareto front is obtained. It is important to note that this method is only optimal with perfect knowledge of the precipitation and assumes that the turbine can react instantaneously to changes in the independent environmental variables.

The method can also be described as follows: choose a constant K and then determine the tip speeds for all independent environmental variables (V_wind, I, …) so that η=K. Since the turbine has a lower and an upper speed limit given by g_min(V_wind) and g_normal(V_wind), respectively, it is not always possible to satisfy η=K. For these cases, the tip speed with the corresponding η closest to K should be chosen.

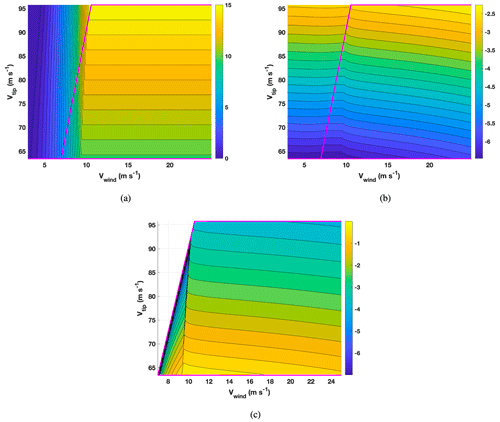
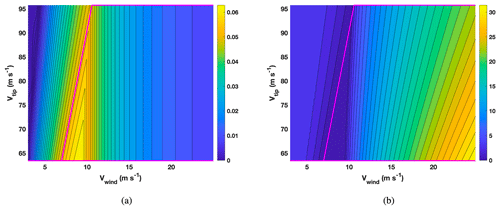
Figure B3 Turbine power, erosion damage production rate and η as a function of V_wind and V_tip according to Eq. (B7). η was rescaled to a range from 0 to 1, and the natural logarithm was applied to the values of (b) and (c) for improved visualization. The magenta piecewise-linear curves indicate the minimum and maximum allowed speed of the turbine (see also Fig. B2), and all drop-size effects are activated for the IEA 15 MW turbine located at De Kooy: (a) P (MW), (b) ln (∂_tD) (s⁻¹) and (c) ln (η).

To understand why Eq. (B7) leads to the optimal ESM strategy, one should consider Fig. B3c. The figure shows η in the space spanned by V_wind and V_tip. As per Fig. B1, the operation at the minimum tip speed during rain represents an optimal strategy (see point B). However, while providing the highest possible LX, this operational point also comes with a large AEP penalty. In practice, another operational point on the Pareto front is likely to be more desirable. To achieve this, the tip speed must increase; however, this also increases the erosion damage production. The aim must be to add the highest growth in power for the smallest growth in damage. This is achieved when starting from the minimum tip speed and then increasing the tip speed for the independent variables (V_wind, I, …) that have the highest $\partial P/\partial \left({\partial }_{t}D\right)$. Since the same value of η might be found for a variety of independent values, contours of η exist. These are shown as black lines in Fig. B3c. Therefore, to find an optimal ESM strategy that satisfies a tuple constraint, one needs, starting from the minimum tip speed, to continuously advance across the η-levels in the direction of increasing tip speeds. This process is stopped when the value of K is found that satisfies the tuple constraint. A contour line thus represents an optimal ESM control curve $g_{\text{opt}}(V_{\text{wind}},I,\mathrm{\dots })$. The Pareto front is formed when the tuples are recorded for every valid value of K.

The approach of Eq. (B6) is valid because the values of η in the region bound by the g_min and g_normal are strictly monotonically decreasing with respect to an increasing tip speed for a particular set of (V_wind, I, …). There are no local minima/maxima or saddle points in the bound region. In the variable load region, g_normal passes through the points of maximum power generation. Above this curve, the power production decreases, even though the tip speed is increased. Hence, above g_normal in the variable load region, the power decreases and η becomes negative. Thus, the turbine produces less power but more damage. This is an operational regime that is clearly undesirable. The properties discussed are true for the IEA 15 MW turbine and for turbines of similar design. Other turbines might behave differently, and in this case, the approach might require modification. It is also noteworthy that this approach only considers damage and AEP loss. The potential influence of repair strategies and their associated costs are not considered. Last but not least, it should be noted that the pitch angle of the blade is precomputed and set according to the method described in Appendix C. The pitch angle is determined so that power production is optimized while at the same time the maximum generator torque is respected. However, since the pitch angle influences P and ∂_tD, it is also possible to consider it a free variable that can be optimized. Or said differently, an ESM could regulate the tip speed and pitch angle to mitigate erosion. This route has not been explored any further in this work.

In a practical implementation, the values of η can be precomputed on a large grid that is spanned by (V_wind, I, …) and V_tip. Hence, for the V-ESM, η is an array of rank 2, while for the VI-ESM, η becomes an array of rank 3. The discretization of V_tip can far exceed the physical limits of the turbine. Subsequently, an appropriate contour line of η=K can be extracted that yields a temporary control curve $g_{\text{opt}}^{\prime }(V_{\text{wind}},I,\mathrm{\dots })$. Subsequently, this curve can be clamped with

$$\begin{array}{}\text{(B8)}& \begin{array}{rl}{g}_{\text{opt}}(V_{\text{wind}},I,\mathrm{\dots })=& \text{clamp}\left(g_{\text{opt}}^{\prime }\right(V_{\text{wind}},I,\mathrm{\dots }),\\ & g_{\text{min}}\left(V_{\text{wind}}\right),g_{\text{normal}}\left(V_{\text{wind}}\right)),\end{array}\end{array}$$

where

$$\begin{array}{}\text{(B9)}& \text{clamp}(x,x_{min},x_{max})=min(max(x,x_{min}),x_{max})\end{array}$$

is the clamping operator. The optimization of one value (K) is required to satisfy a particular tuple. Solving this optimization problem is trivial, e.g., by simply calculating all tuples for all K. The computational cost of the proposed approach is minimal and is similar to the C-ESM. The derivatives of $\partial P/\partial V_{\text{tip}}$ and $\partial \left({\partial }_{t}D\right)/\partial V_{\text{tip}}$ can be computed using a simple finite difference scheme. The magnitude of η might not always be convenient since $P\gg {\partial }_{t}D$. The power production is on the order of MW; hence P≈10⁶ to P≈10⁷, while the order of the total damage accumulated per year is $D\approx {\mathrm{10}}^{-\mathrm{2}}$ to D≈10⁰. Consequently, assuming the latter, the damage production rate (in s⁻¹) becomes ${\partial }_{t}D\approx {\mathrm{10}}^{-\mathrm{8}}$. Hence, for the constituents of η, a considerable difference in magnitudes exists. Therefore, performing a rescaling operation can be advantageous. It is important to note that rescaling does not influence the resulting control curve g_opt but is merely a question of convenience in the actual implementation.

The damage rate calculation is dependent on the mode considered. For the V-ESM, the damage rate reads

$$\begin{array}{}\text{(B10)}& {\partial }_t{D}_{\text{V-ESM}}\left(g_{\text{opt}}\right(V_{\text{wind}}\left)\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}\mathit{°}}{\overset{\mathrm{360}\mathit{°}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\partial }_t{D}_{\mathrm{I},\mathit{\theta },\mathit{\varphi }}\mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }\mathrm{d}I.\end{array}$$

For the VI-ESM, the damage rate becomes

$$\begin{array}{}\text{(B11)}& {\partial }_t{D}_{\text{VI-ESM}}\left(g_{\text{opt}}\right(V_{\text{wind}},I\left)\right)=\underset{\mathrm{0}\mathit{°}}{\overset{\mathrm{360}\mathit{°}}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\partial }_t{D}_{\mathit{\theta },\mathit{\varphi }}\mathrm{d}\mathit{\varphi }\mathrm{d}\mathit{\theta }.\end{array}$$

When comparing Eqs. (B10) and (B11) with Eq. (1), one can see that for every independent variable that drives the ESM, the respective integral must be removed. Therefore, the V-ESM depends on f_I,f_θ and f_ϕ,plane, whereas the VI-ESM depends on f_θ and f_ϕ,plane. Conversely, this shows that the distribution of wind at a particular site does not influence the V-ESM and VI-ESM η contours. Expanding on this, the VI-ESM η contours are also independent of the rain intensity distribution of the site. Both ESM strategies depend on the drop-size distribution f_ϕ,plane. In practice, f_ϕ,plane varies according to the site (Pryor et al., 2022). Hence, one can conclude that for an optimal ESM strategy, the site-specific drop-size distribution should be taken into account.

The contours of the V-ESM's power and damage accumulation rate are shown in Fig. B3a and b. In the variable load region, the isocontour lines of the damage accumulation rate are almost flat. In the rated power region, the isocontour lines start falling due to the interplay of the increasing wind speed and pitch angle. The isocontour lines of P are flat in the rated power region. This is due to the turbine being torque limited in this region, and an increase in the power can only come from an increase in the rotational speed (see Eq. C1). In the variable load region, the power isocontour lines are almost vertical, and hence the power changes rapidly with the tip speed. For the numerical calculation of the derivatives, it is important to use a sufficiently fine grid in this region. Additionally, any interpolation scheme must have a sufficiently high continuity to avoid erroneous discontinuities in the contour plot of η. The resulting η_V-ESM is visualized in Fig. B3c for the operational space. It can be seen that η decreases with increasing tip speed. Close to the minimum tip speed, η predicts that an increase in tip speed will yield a considerable increase in power for only a moderate increase in damage production. However, as the tip speed increases, due to the high value of β, η reduces rapidly; this is a consequence of the order of the damage and power terms. The damage scales with the tip speed according to approximately β+1, while the power scales with about an order of 1. Therefore, in comparison, a change in the wind speed only marginally affects power but greatly affects erosion damage production.

Figure B4 Resultant VI-ESM control curve for a particular K according to Eq. (B6), as well as slices through the volumetric data of η as a function of V_wind and I. In the slices, the magenta-colored curves represent the surface of panel (a); the natural logarithm was applied to η for improved visualization, and all drop-size effects are activated for the IEA 15 MW turbine located at De Kooy: (a) g_opt for an arbitrary value of K in Eq. (B6), black grid for visualization; (b) a slice through the volumetric data of η in the V_wind–V_tip plane (the black lines show the isocontours of η) and (c) a slice through the volumetric data of η in the I–V_tip plane (the black lines show the isocontours of η).

The extension of the V-ESM to the VI-ESM is straightforward. Instead of Eq. (B10), Eq. (B11) must be used. Figure B4a shows a resulting ESM strategy based on an arbitrary value of K. For I=0, i.e., no rain, the ESM strategy retains the original control curve of the turbine. As the rain intensity increases, the curve starts to fall in the direction of increasing rain intensities. The fall is similar to a parabolic curve. In the direction of V_wind, the VI-ESM strategy is similar to the V-ESM strategy. Two slices through the volumetric data of η are given in Fig. B4. The first slice, given in Fig. B4b, shows η in the V_wind–V_tip plane. This slice is very similar to Fig. B3c. Hence, the prior observations pertain to it. In Fig. B4c the slice in the I–V_tip plane is given. One can see how the isocontours fall as the rain intensity increases. This aligns with earlier observations that higher rain intensities produce much more damage than lower rain intensities.

Figure B5 shows the resulting optimal Pareto fronts of the V- and VI-ESM. As with any ESM strategy, the start and end points of both modes are equal (see points A and B in Fig. B1). In between these points, the VI-ESM can achieve a significantly higher lifetime extension than the V-ESM and can, therefore, be considered superior. For example, at 1 % AEP loss, the V-ESM provides a lifetime extension of about 7, whereas the VI-ESM offers an extension of about 13.1. The increase in performance comes with a shift in shape. The V-ESM produces a convex curve, whereas the graph of the VI-ESM is first convex and then becomes concave toward the maximum lifetime extension. This change in shape is associated with a shift in the Pareto front upwards and to the left, thus in the favorable direction as indicated in Fig. B1.

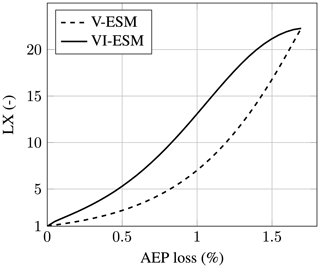
Figure B5 Resulting Pareto fronts for the V-ESM and VI-ESM using the optimal approach from Eq. (B6); all drop-size effects are activated for the IEA 15 MW turbine located at De Kooy.

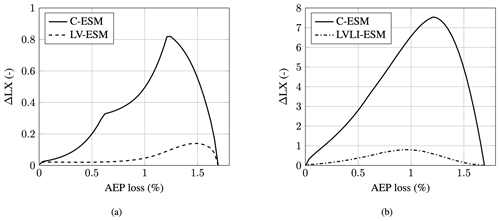
Figure B6 Differences in lifetime extension between the optimal and heuristic ESM strategies for the IEA 15 MW turbine located at De Kooy: (a) V-ESM as baseline and (b) VI-ESM as baseline.

Heuristic reference ESM strategies are considered to support the claim of Eq. (B6). The V-ESM and VI-ESM are tested against the heuristic C-ESM used in Barfknecht et al. (2022). Additionally, two other strategies are considered. The first is a more sophisticated rule where the control curve comprises two piecewise-linear line segments. For that, $\mathrm{\Delta }V=V_{\text{wind}}-V_{\mathrm{15}}$ is defined, where V₁₅ = 6.98 m s⁻¹, which is the wind speed at the end of IEA 15 MW's minimum rotor speed control region; see Gaertner et al. (2020). The equation reads

$$\begin{array}{}\text{(B12)}& \begin{array}{rl}& \text{LV-ESM}=\\ & \left\{\begin{array}{ll}{g}_{\text{normal}}\left(V_{\text{wind}}\right)& \text{if }I=\mathrm{0},\\ \text{clamp}(min(C_{\mathrm{2}}\mathrm{\Delta }V+\mathrm{1},C_{\mathrm{1}}),\mathrm{1},& \\ \frac{g_{\text{normal}}\left(V_{\text{wind}}\right)}{g_{\text{min}}\left(V_{\text{wind}}\right)}\left)g_{\text{min}}\right(V_{\text{wind}})& \text{if }I>\mathrm{0}.\end{array}\right.\end{array}\end{array}$$

The second is an extension that adds a dependency on I. This creates a rule consisting of three piecewise-linear planes. It uses the definition $\mathrm{\Delta }I=I-C_{\mathrm{4}}$. The equation reads

$$\begin{array}{}\text{(B13)}& \begin{array}{rl}\text{LVLI-ESM}=& \text{clamp}(min(C_{\mathrm{3}}\mathrm{\Delta }I+C_{\mathrm{2}}\mathrm{\Delta }V+\mathrm{1},C_{\mathrm{1}}),\\ & \mathrm{1},{\displaystyle \frac{g_{\text{normal}}\left(V_{\text{wind}}\right)}{g_{\text{min}}\left(V_{\text{wind}}\right)}}\left)g_{\text{min}}\right(V_{\text{wind}}).\end{array}\end{array}$$

For both equations, the coefficients $C_{\mathrm{1}},\mathrm{\dots },C_{\mathrm{4}}$ are required. LV stands for linear with respect to V_wind. The acronym LI stands for linear with respect to I. Matlab's fmincon function was used to find the coefficients. A particular target AEP loss was defined and then the coefficients that led to the highest lifetime extension were selected. This resulted in Fig. B6, which compares the performance of the V-ESM and VI-ESM to the heuristic C-ESM, LV-ESM and LVLI-ESM strategies. The figure plots the difference in lifetime extension $\mathrm{\Delta }\text{LX}=L{X}_{\text{optimal}}-L{X}_{\text{heuristic}}$ against the corresponding AEP loss.

As shown in Fig. B6a, the C-ESM offers up to 0.8 less LX in comparison to the V-ESM. The LV-ESM performs significantly better, performing almost as well as the V-ESM in some parts. The good performance of the LV-ESM can be explained by its form of two piecewise-linear segments. These allow for a close approximation of η's ideal contour lines as shown in Fig. B3c.

Figure B6b shows that the maximum deficit in LX of the LVLI-ESM compared to the VI-ESM is about 0.8. The contours of η in the direction of the rain intensity have the shape of a falling parabolic curve; see, for example, Fig. B4c. The linear approximation of the LVLI-ESM seems to deliver good performance in this region. To conclude, it is shown that the heuristic methods considered can, in some regions, approach the performance of the optimum ESM but cannot exceed its performance.

While heuristic methods can provide a reasonably good approximation of the optimal solution, differences still exist. A ΔLX=0.8 is still significant considering that it is merely the result of an offline optimization problem. A further argument for the optimum ESM stems from the following anecdotal evidence: for the authors of this paper, the implementation of the optimum ESM was quite straightforward. However, the optimization of the coefficients of the LV-ESM and LVLI-ESM proved to be challenging. As stated, the optimization was performed with Matlab's fmincon function. Careful consideration had to be paid to the settings chosen. Often, the results would not converge to the optimum set of coefficients. Overall, the optimization of the (worse-performing) heuristic curves consumed significantly more time from the authors and required more computational resources.

Appendix C: Calculation of the AEP and pitch angle

The method to compute the turbine's power is important for the ESM and, as will be shown, is also important for the damage calculation. It is, therefore, described here in more detail. The fundamental formula for the turbine power P is

$$\begin{array}{}\text{(C1)}& P=Q\mathit{\omega },\end{array}$$

where Q and ω are the rotors' torque and rotational speed, respectively. A maximum generator torque Q_max that cannot be exceeded exists. Therefore, at all times, the following condition must hold:

$$\begin{array}{}\text{(C2)}& Q\le Q_{max}.\end{array}$$

For maximum power, Q should be maximized at all times without exceeding Q_max. The torque coefficient is found with the following formula:

$$\begin{array}{}\text{(C3)}& \begin{array}{rl}& C_{\mathrm{Q}}\left(\mathit{\lambda }\right)=\\ & \left\{\begin{array}{ll}M\left(\mathit{\lambda }\right)& \text{if }M\left(\mathit{\lambda }\right)<\left(C_{Q_{max}}=\frac{Q_{max}}{qAR}\right),\\ \left(C_{\mathrm{Q}}(\mathit{\lambda },{\mathit{\phi }}_{\text{pitch}})=C_{Q_{max}}\right)& \text{if }M\left(\mathit{\lambda }\right)\ge C_{Q_{max}},\end{array}\right.\end{array}\end{array}$$

where $M\left(\mathit{\lambda }\right)=max\left(C_{\mathrm{Q}}\right(\mathit{\lambda },{\mathit{\phi }}_{\text{pitch}}\left)\right)$, and λ is the tip-speed ratio. q is the dynamic pressure of the wind, A is the rotor disk area and R is the rotor radius. φ_pitch is found by determining where either C_Q is maximum or $C_{\mathrm{Q}}=C_{Q_{max}}$. The resulting pitch is used in the calculation of the damage; see Eqs. (20) and (30). From the tip-speed ratio, the pitch angle and the position along the blade, the corresponding local induction factors can be found. This study assumes that the wind shear exponent is zero. Hence, the V_wind is constant over the rotor disk. If the wind shear exponent is included, it leads to local changes in the tip-speed ratio and will make the local induction factors a function of the blade angular position.

CCBlade, in conjunction with the IEA 15 MW's yaml ontology file, was used to find the torque coefficient as a function of the tip-speed ratio and the blade pitch angle (Ning, 2014). The induction factors are also given in the output of CCBlade. The torque coefficient and pitch angle are plotted in Fig. C1. The torque coefficient is decreased when the turbine enters the rated power region. This is done by adjusting the pitch angle so that the maximum generator torque is not exceeded. The figure shows that pitch angles of over 30° are encountered. Angles of this magnitude impact the damage significantly; see Eqs. (30), (31) and (38). Therefore, the pitch angle needs to be properly accounted for.

The resulting AEP can be calculated using

$$\begin{array}{}\text{(C4)}& \text{AEP}=T_{\text{year}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}P{f}_{\mathrm{I}}{f}_{\text{wind}}\mathrm{d}{V}_{\text{wind}}\mathrm{d}I.\end{array}$$

For normal turbine control or for an ESM that is solely controlled based on the wind speed, the integral (and corresponding probability density function) over the rain intensity can be omitted.

Figure C1 Contour plots of the torque coefficient and pitch angle as a function of wind speed and tip speed; the magenta curves enclose the operational regime of the turbine for the IEA 15 MW turbine: (a) torque coefficient, C_Q (–), and (b) pitch angle, φ_pitch (°).