Do wind turbines pose roll hazards to light aircraft?

Wind energy accounted for 5.6 % of all electricity generation in the United States in 2016. Much of this development has occurred in rural locations, where open spaces favorable for harnessing wind also serve general aviation airports. As such, nearly 40 % of all United States wind turbines exist within 10 km of a small airport. Wind turbines generate electricity by extracting momentum from the atmosphere, creating downwind wakes characterized by wind-speed deficits and increased turbulence. Recently, the concern that turbine wakes pose hazards for small aircraft has been used to limit wind-farm development. Herein, we assess roll hazards to small aircraft using large-eddy simulations (LES) of a utility-scale turbine wake. Wind-generated lift forces and subsequent rolling moments are calculated for hypothetical aircraft transecting the wake in various orientations. Stably and neutrally stratified cases are explored, with the stable case presenting a possible worst-case scenario due to longer-persisting wakes permitted by lower ambient turbulence. In both cases, only 0.001 % of rolling moments experienced by hypothetical aircraft during down-wake and cross-wake transects lead to an increased risk of rolling.

1 Introduction

Due to its appeal as a renewable, low-carbon energy source, wind energy development has increased rapidly, accounting for 5.6 % of electricity generation in the United States at the end of 2016 (EIA, 2017). Wind turbines generate electricity by extracting momentum from the atmosphere, thereby creating wakes characterized by a wind-speed deficit and increased turbulence downwind (Baker and Walker, 1984; Lissaman, 1979; Sforza et al., 1981). As the size of turbine rotors increases, turbine wakes also increase, which may pose a greater hazard to nearby flying aircraft (Wang et al., 2015). Therefore, improved understanding of turbine wake characteristics is crucial to assess hazards to aircraft posed by wakes.

Numerous studies have investigated the structure, duration, and decay of wind turbine wakes. Most of these studies address wake impacts on surface temperature (Rajewski et al., 2013; Smith et al., 2013; Zhou et al., 2012) or surface fluxes (Rajewski et al., 2014, 2016). Detailed measurements of winds in turbine wakes have been taken with lidars (e.g., Aitken et al., 2014a; Iungo et al., 2012; Käsler et al., 2010; Rhodes and Lundquist, 2013). Wind tunnel experiments have also been used to further aerodynamic research on wind turbines (Chamorro and Porté-Agel, 2009; Hancock and Zhang, 2015; Snel et al., 2007; Vermeer et al., 2003; Yang et al., 2012). Scaling such experiments to utility-scale turbines can be challenging: wind tunnel measurements typically cannot account for complexities in atmospheric profiles, such as inversions and wind veer. Computational fluid dynamics (CFD) simulations of wind turbine wakes provide insights into turbine wakes (Sanderse et al., 2011). Both actuator-disk (Calaf et al., 2010; Mirocha et al., 2014; Vanderwende et al., 2016; Vermeer et al., 2003) and actuator-line (Churchfield et al., 2012; Marjanovic et al., 2017; Sørensen and Shen, 2002; Troldborg et al., 2010) methods have been used to simulate the rotor and downstream flow to study wake structure.

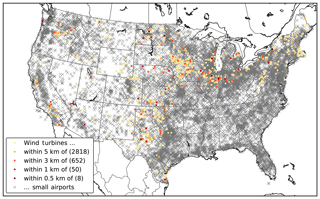
Extensive wind development occurs in rural locations, where open spaces favorable for wind energy are also home to numerous general aviation airports. Almost 40 % of all wind turbines in the United States exist within 10 km of a small airport and about 5 % exist within 5 km of a small airport (Fig. 1, based on data from OurAirports, 2016; USGS, 2014). Currently, neither the Federal Aviation Administration (FAA) of the United States nor the Civil Aviation Authority (CAA) of the United Kingdom have detailed recommendations on the effects of wind-turbine-induced roll hazards for aircraft (CAA, 2012; Ho et al., 2014).

General aviation pilots are typically most concerned with the rolling moment (Wang et al., 2015), and we thus focus our study on this hazard. The rolling moment is the tendency for an aerodynamic force applied at a distance from an aircraft's center of mass to cause the aircraft to undergo angular acceleration about its roll axis, considered a torque in this study (Etkin and Reid, 1996). The roll axis is the longitudinal axis, running from the nose to the tail of the aircraft. Other wake hazards of concern to pilots are those generated from the wings of preceding aircraft during take-off as a consequence of lift (Gerz et al., 2009; Holzäpfel et al., 2007).

Previous work has argued that turbine wakes present, in particular, a serious roll hazard to general aviation aircraft. Mulinazzi and Zheng (2014) used a helical vortex model to represent a wind turbine wake from which aircraft roll hazards were calculated. The helical vortex model was scaled up from a wind tunnel study using miniature turbines with a rotor diameter of 0.254 m. The 4 m s⁻¹ inflow was meant to trigger transient helical tip vortices (Yang et al., 2012). Mulinazzi and Zheng (2014) scaled up these wind tunnel results to the atmosphere by assuming comparable near- and far-wake turbulent flow structures between the tip vortices measured in the wind tunnel and the full wake produced in a real atmosphere by a utility-scale turbine. With calculations derived from this scaling, they suggest wind turbine wakes pose a significant roll hazard to general aviation aircraft at downwind distances as far as 4.57 km (2.84 miles) (Mulinazzi and Zheng, 2014). These findings have been used in multiple states to limit wind energy development. Reid Bell, airport manager at Pratt Regional Airport in Kansas, confirmed that the Pratt wind-farm project was relocated further away from the airport as a direct result of the Mulinazzi and Zheng (2014) study (Williams, 2014). The study has been used as a warning to aviators in Virginia as well (Hamilton, 2014).

Other researchers have also investigated the hazards that wind turbines pose to aircraft by computing the roll hazards from analytic representations of wakes. van der Wall et al. (2016) and van der Wall and Lehmann (2017) found that typical onshore turbines could pose hazards for gliders or ultralight helicopters but perhaps not for general aviation aircraft. Wang et al. (2015, 2017) computed a wake wind field derived using the Beddoes circulation formula (Madsen and Rasmussen, 2004), proven to adequately match lidar field observations made of a wind turbine wake. For a 30 m rotor diameter wind turbine, Wang et al. (2015, 2017) find that the wake does not pose any roll hazards for aircraft five rotor diameters downstream from the turbine.

Rather than approximating wakes, we seek to explicitly resolve turbine wakes within a dynamic, non-stationary atmosphere. We therefore use large-eddy simulations (LES) to assess wind-generated roll hazards to small aircraft from the wake of a utility-scale wind turbine. Section 2 provides details on our simulations and methodology for analyzing the model data. Section 3 presents the results of our analysis, specifically the quantified roll hazards on hypothetical aircraft. We conclude in Sect. 4 with a discussion of our results and suggestions for future work.

2 Methods

2.1 Simulations

LES is a well-established method for studying wind turbine wakes. LES have been used to investigate wind turbine wake turbulence (Churchfield et al., 2012; Jha et al., 2015), the wind-farm boundary layer (Calaf et al., 2010), and the evolution of the wake structure in variable stability conditions and throughout the diurnal cycle (Abkar et al., 2016; Aitken et al., 2014b; Bhaganagar and Debnath, 2014; Englberger and Dörnbrack, 2018; Lu and Porté-Agel, 2011; Mirocha et al., 2014, 2015). Jimenez et al. (2007) find good agreement between LES and experimental data of turbine wakes, which has led to the use of LES to correct for instrumentation error (e.g., Lundquist et al., 2015).

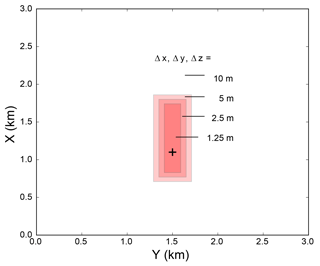
Figure 2 Schematic of the SOWFA mesh, with model resolutions labeled at their respective locations in the domain. Turbine location is denoted by the plus sign.

Representing turbines in LES can be done via actuator disks, where the turbine rotor is represented by a permeable circular disk with uniformly distributed thrust forces (Aitken et al., 2014b; Calaf et al., 2010; Mirocha et al., 2014; Vanderwende et al., 2016; Vermeer et al., 2003) or by actuator lines, which represent the turbine blades as separate rotating lines (Nilsson et al., 2015; Porté-Agel et al., 2011; Sørensen and Shen, 2002). Martínez-Tossas et al. (2015) compare actuator-line and actuator-disk models and conclude that they produce similar wake profiles; however, the actuator-line model can generate fine flow structures near the blades such as root and tip vortices that the actuator-disk model cannot.

We perform our simulations using the Simulator fOr Wind Farm Applications (SOWFA; Churchfield and Lee, 2014; Fleming et al., 2013). SOWFA is a computational fluid dynamics solver coupled with a turbine dynamics model. The LES solver is based on the Open Field Operations and Manipulation (OpenFOAM) toolbox version 2.4.x (OpenCFD, 2016). OpenFOAM is a set of C++ libraries and applications for use in solving the partial differential equations describing fluid flow. The simulations utilize the same two-step methodology as described in Churchfield et al. (2012), briefly summarized here. First, a precursor LES generates turbulent atmospheric flow on a domain with idealized periodic lateral boundaries. Once the turbulent boundary layer reaches quasi-equilibrium, a plane of turbulent data from the upwind lateral boundary is saved at each time step to be used as inflow boundary conditions for the simulation with the turbine. Next, a turbine is introduced into the flow initialized from the quasi-equilibrium precursor flow field. The side boundaries remain periodic, but the saved velocity and temperature data from the precursor are used as inflow Dirichlet boundary conditions for this simulation. The outflow boundary uses Neumann, zero-normal-gradient conditions. Like the precursor, the overall domain size is 3 km × 3 km in the horizontal and 1 km in height, but variable resolution is used. Most of the domain has 10 m resolution, like the precursor, but around the turbine and its wake the resolution is gradually refined to 1.25 m (Fig. 2). The time step in the wind turbine simulation is restricted to capture the motion of the blade tips.

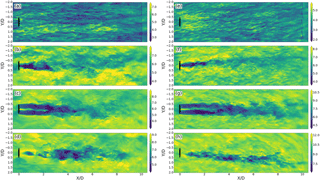
Figure 3 Contoured horizontal cross sections of horizontal wind speeds (m s⁻¹) comparing the neutral (a–d) and stable (e–h) cases at the near surface (1 m; a, e), rotor bottom (40 m; b, f), rotor center (80 m; c, g), and rotor top (120 m; d, h).

The turbine model consists of an actuator-line representation of turbine blades (Sørensen and Shen, 2002), proven to adequately capture the generation and downstream evolution of helical tip vortices (Churchfield et al., 2017; Ivanell et al., 2010; Lignarolo et al., 2015; Martínez-Tossas et al., 2017; Toloui et al., 2015). We model the GE 1.5-MW SLE wind turbine (Mendoza et al., 2015), a utility-scale turbine often deployed in standard industrial wind farms. This horizontal-axis, upwind turbine has a three-bladed rotor 77 m in diameter, with a hub height of 80 m. While not the largest turbine type currently available, the GE 1.5-MW SLE is one of the most widely deployed turbines worldwide, making the wake effects on general aviation aircraft explored herein broadly applicable to numerous wind farms.

A subvolume of the flow surrounding the turbine and wake was sampled at 1 Hz. This sampled subvolume uses a Cartesian coordinate system, within which positive x (y) corresponds to downwind (crosswind) and positive z corresponds to height above the surface. In all cases, the sampled subvolume extends 11 rotor diameters (D) in the x (downwind) direction, 4 D in the y (crosswind) direction, and 3 D in the vertical direction. The computational grid resolution is approximately 1.25 m, uniform in all directions (Fig. 2). This high resolution is necessary to adequately resolve flow structures that impact small (10 m) general aviation aircraft.

Previous observations note turbine wakes tend to diffuse more rapidly in convective conditions because the high ambient turbulent kinetic energy (TKE) of the surrounding air induces mechanical mixing to erode the wake (Baker and Walker, 1984; Bhaganagar and Debnath, 2014; Magnusson and Smedman, 1994; Mirocha et al., 2015). We thus hypothesize that stable conditions, with low TKE and a low turbulent eddy dissipation rate (EDR) (Bodini et al., 2018), present a worst-case scenario for general aviation aircraft due to longer-persisting wakes permitted by the reduced ambient TKE and EDR. As such, we simulate a neutral case and a stable case. Each simulation is spun up for 30 000 s, after which 100 s of data are output. The neutral case has a hub height inflow wind speed of 7.4 m s⁻¹ and a constant potential temperature profile of 300 K, while the stable case has a hub height inflow wind speed of 9.4 m s⁻¹ and potential temperature lapse rate of −0.024 K m⁻¹ over the vertical extent of the domain. These wind speeds were selected because of their location on the power curve: above the cut-in wind speed (3 m s⁻¹) and below the rated wind speed (12 m s⁻¹), which is a range conducive for generating wakes and typical for general aviation flight conditions.

Horizontal slices of the horizontal wind speed (Fig. 3) show the wake characteristics at the near surface and bottom, center, and top of the rotor disk for both cases. The wake in the neutral case is approximately symmetric throughout the rotor disk (Fig. 3b–d), with the two-lobed profile becoming approximately Gaussian around 3 D (Fig. 3c). In the stable case, the wake exhibits a more asymmetric structure and veers with altitude (Fig. 3f–h) due to ambient background veer, as in other stable simulations of wakes (Lundquist et al., 2015). The horizontal extent and width of the wake also differ with stability. The stable conditions enable the wake to maintain a narrower structure and longer downwind presence, as opposed to the neutral conditions that form a comparatively more diffuse and shorter wake. The noise visible in both cases past 8 D is due to a combination of the coarser grid resolution and high sampling resolution in that region of the domain.

2.2 Data analysis

We use the simulation data to quantify potential roll hazards on hypothetical general aviation aircraft transecting the turbulent wake. The Cessna 172, a common general aviation aircraft, has a wingspan of 10 m, a planform area of 16 m², and an aspect ratio of 7 (Cessna Aircraft Company, 2004). We represent the aircraft in the LES data as a 10 m line. The 1.25 m resolution of the data allows the line to be divided into eight segments – four points diverging from center to represent the two wings. We then use the LES wind vectors observed at each point on the aircraft to make calculations of the roll hazard metrics: rolling moment and rolling moment coefficient.

The rolling moment is computed from the lift distribution across the aircraft's wingspan. At each of the eight points on the aircraft, we sample the oncoming wind velocity vector nonparallel to the wing line. We assume a typical landing flight speed of a general aviation aircraft of 35 m s⁻¹; the sampled wind vectors are relative to the movement of the aircraft. Thus, the total velocity vector, or true airspeed, is calculated at each segment: the nonparallel component of the wind vector impinging on the wing, added to the flight velocity. The elevation angle of each motion-relative total velocity vector forms an angle of attack α along the wing:

$$\begin{array}{}\text{(1)}& \mathit{\alpha }\equiv {\tan }^{-\mathrm{1}}{\displaystyle \frac{\mathit{w}}{\mathit{V}}},\end{array}$$

where w is the instantaneous component of velocity in z and V is the true instantaneous airspeed. From each angle of attack, a coefficient of lift C_l is derived – eight in total along the aircraft:

$$\begin{array}{}\text{(2)}& C_{\mathrm{l}}=\mathrm{2}\mathit{\pi }\mathit{\alpha }+C_{\mathrm{l},\mathrm{0}}=C_{\mathrm{l},\mathrm{b}}+C_{\mathrm{l}}^{\prime },\end{array}$$

where C_l, 0 is the lift coefficient at zero angle of attack, C_l, b is the base coefficient of lift, $C_{\mathrm{l}}^{\prime }$ is the lift perturbation, and 2πα is the chosen C_l–α curve provided by thin airfoil theory, an accurate idealization for most airfoils at small angles of attack.

The dimensional lift perturbation $L_i^{\prime }$ of each segment of the aircraft is then derived from the coefficient of lift:

$$\begin{array}{}\text{(3)}& L_i^{\prime }=\mathrm{0.5}{C}_{\mathrm{l}}^{\prime }\mathit{\rho }|\mathit{V}{|}^{\mathrm{2}}A,\end{array}$$

where A is the planform area of the segment and ρ is the standard near-sea-level atmosphere density of 1.225 kg m⁻³ to reflect the altitude of interest for wake-transecting aircraft.

To calculate the rolling moment M_roll, we sum the eight lift values across the length of the wing

$$\begin{array}{}\text{(4)}& M_{\mathrm{roll}}=\sum _{i=\mathrm{1}}^N{L}_i^{\prime }{r}_i,\end{array}$$

where N is the total number of points along the aircraft and r_i is the distance from the center of the aircraft, which is positive (negative) to the left (right) of center from the perspective of the aircraft.

Finally, the rolling moment coefficient C_roll is calculated by normalizing the rolling moment by the size of the aircraft

$$\begin{array}{}\text{(5)}& C_{\mathrm{roll}}={\displaystyle \frac{\mathrm{2}{M}_{\mathrm{roll}}}{\mathit{\rho }|\mathit{V}{|}^{\mathrm{2}}Sb}},\end{array}$$

where $\left|\mathit{V}\right|$ is the true airspeed averaged across the eight segments, S is the total planform area of the aircraft, and b is the wing span of the aircraft, which we set to be 10 m to align with the general aviation Cessna 172 detailed earlier (Etkin and Reid, 1996).

The representation of an aircraft as a straight line within the LES data requires several assumptions. For simplicity, we assume a rectangular wing with some base lift equal to the aircraft weight, a result of defining a finite C_l, 0 and some constant aircraft angle of attack. We then only consider a lift perturbation $C_{\mathrm{l}}^{\prime }$ from this base lift, as the remaining lift distribution is equal on both sides of the wing, contributing no rolling moment. We also note that our calculations assume that the aircraft and the flow field do not interact beyond the first-order effects on the aircraft and thus do not account for any aircraft motion response due to varying forces. A true depiction of aircraft motion would require a 6-degrees-of-freedom aircraft model and solver, which is more complicated than this study warrants. We recognize that by not accounting for the aircraft motion response, these calculations may omit cases when the changing wind components on the wing could result in higher rolling moments. However, such an additional series of calculations would introduce uncertainty because of the role of pilot response, and we argue that the wake roll hazards encountered (to be explained in Sect. 3) would allow a pilot to quickly correct against wake-turbulence-induced roll instead of allowing roll to escalate.

We define 540 total flight tracks through the LES data to sample the wind vectors and make the above calculations. These flights are conducted with two different orientations: down-wake transects and cross-wake transects. The down-wake group, 100 aircraft flight paths separated by 15 grid points (∼18.5 m) in y and z, is centered over the wake. We march these aircraft downwind from the turbine through the x extent of the domain. The cross-wake group is comprised of 44 rows and 10 columns of aircraft flight paths separated by 15 grid points (∼18.5 m) in x and z initially positioned at $y=-\mathrm{2}D$, which is the furthest west point of the domain. We march these aircraft through the y extent of the domain, perpendicular to the wake. The cross-wake aircraft descend at a 3^∘ angle to emulate a typical landing pattern. At each advancing increment in the transect (682 points down-wake, 247 points cross-wake), the rolling moment (Eq. 4) and rolling moment coefficient (Eq. 5) are calculated for all 540 aircraft, yielding 176 880 instances for each roll hazard calculation. We define one additional down-wake flight track far outside of the wake ($y=-\mathrm{1.9}D$, z=100 m) to serve as a constant, wake-free flight path for comparison. The aircraft do not interact with each other nor modify the flow field as they transect the wake. All calculations are made during a single one-second time step where the aircraft fly across a frozen domain. This process is then repeated for each of the 100 time steps available, yielding 17 688 000 total hazard calculations.

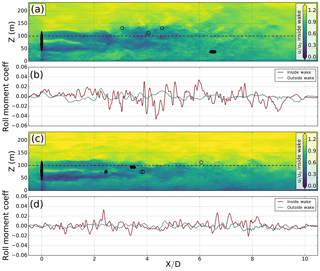
Figure 4 Comparison of rolling moment coefficient (b, d) between the flight path inside (red) and outside (blue) of the turbine wake in the neutral (a, b) and stable (c, d) cases. The vertical cross section of the downwind component of the wind velocity u, scaled by inflow wind speed u₀, 7.4 and 9.4 m s⁻¹ in neutral and stable conditions, respectively, at the turbine location (y=0; a, c) is contoured for reference, over which the height of the flight paths (z=100 m) is traced in a red dashed line. The dots represent the downwind and vertical location of the three highest rolling moment coefficients experienced by the down-wake (black) and cross-wake (empty) array of aircraft.

3 Results

We first analyze the turbine wake impacts on a hypothetical general aviation aircraft by comparing roll hazard calculations of a sample flight track outside of the wake to those within the wake. Rolling moment coefficient (Eq. 5) is calculated for an aircraft inside and outside the wake for the neutral (Fig. 4b) and stable (Fig. 4d) cases to categorize each moment as a “low”, “medium”, or “high” hazard as used in the Mulinazzi and Zheng (2014) and Wang et al. (2015) assessments of wake roll hazards. These assessment criteria are based on the maximum rolling moment that the aileron on a typical aircraft can generate to counteract a moment induced by the wake field (Wang et al., 2015). A wake-induced rolling moment coefficient $\left|C_{\mathrm{roll}}\right|$ above 0.28 is considered a high hazard, between 0.1 and 0.28 a medium hazard, and below 0.1 a low hazard. As expected, in both stability conditions, the aircraft inside the wake experiences higher values of rolling moment coefficient, indicating increased turbulence of the turbine wake. However, rolling moment coefficients experienced in both stability cases for the aircraft inside the wake remain within the low hazard threshold of $\left|C_{\mathrm{roll}}\right|\mathit{<}\mathrm{0.1}$.

While these sample aircraft flight tracks in Fig. 4b, d show an example for one location in the wake, the LES data set allows us to calculate more instances of roll hazards throughout the entire wake. More conclusive results can be seen by assessing the 540 flight paths down and across the wake spanning all 100 s of data. We summarize occurrences of roll hazard calculations via histograms of neutral (Fig. 5a, b) and stable (Fig. 5c, d) cases and down-wake (Fig. 5a, c) and cross-wake (Fig. 5b, d) transects as a function of the downwind distance from the turbine.

Table 1 Summary of roll hazards

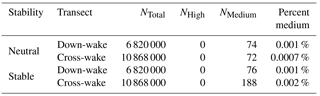
In all transects and stabilities, over 99.99 % of all calculations exist within the low hazard threshold. Table 1 lists detailed counts of instances classified as medium hazards ($\mathrm{0.1}\mathit{<}\left|C_{\mathrm{roll}}\right|\mathit{<}\mathrm{0.28}$). The stable cross-wake configuration has the greatest fraction of medium hazards at 188 out of 10 868 000. Across all cases, no moments reach the high hazard threshold. Further, the vast majority of calculated roll hazards are even smaller than the maximum low hazard limit ($\left|C_{\mathrm{roll}}\right|\mathit{<}\mathrm{0.1}$) and are contained within $\left|C_{\mathrm{roll}}\right|\mathit{<}\mathrm{0.02}$ (Fig. 5). The decreasing frequency of rolling moment coefficients $\left|C_{\mathrm{roll}}\right|$ greater than 0.02 beyond 8 D suggests that roll hazards decrease with downstream distance at this point (Fig. 5). While we hypothesized the stable case would generate more hazardous rolling moment coefficients, we find similar fractions of medium hazards in the stable conditions as in neutral (Fig. 5). Even though stable conditions enable the wake to persist longer downwind than in convective conditions, they do not increase turbulence that would pose hazards for general aviation aircraft.

The largest roll hazards, as indicated by C_roll, occur most frequently about 5 D downwind from the turbine (Fig. 5). The three highest roll hazards in the neutral, down-wake case ($C_{\mathrm{roll}}=\mathrm{0.128},\mathrm{0.124},\mathrm{0.123}$) all occur in a sequential line downwind near 6.5 D in the bottom-left quadrant of the rotor disk as looking downwind (black circles in Fig. 4a). These rolling moment coefficients are all positive, indicating clockwise rotation about the aircraft's longitudinal axis when looking downwind. In the neutral, cross-wake case, the three highest rolling moments ($C_{\mathrm{roll}}=\mathrm{0.127},\mathrm{0.124},\mathrm{0.124}$) occur between 3 and 4.5 D in the top-right quadrant of the rotor disk (empty circles in Fig. 4a). For the stable, down-wake case, the highest two roll hazards ($C_{\mathrm{roll}}=-\mathrm{0.121}$, −0.12) occur at 3.5 D downwind, in the top-left quadrant of the rotor (Fig. 4c). The next highest hazard ($C_{\mathrm{roll}}=-\mathrm{0.119}$) occurs 2.5 D downwind, differing from the prior hazards by residing in the bottom-left quadrant of the rotor (Fig. 4c). The largest hazards across all cases occur in the stable, cross-wake case at C_roll=0.14, 0.14, 0.136, with the first two in the bottom-right quadrant of the rotor disk and the third in the top left (empty circles in Fig. 4c). All of these peak hazards are located in the high-shear zone at the edge of the wake between 3 and 7 D downwind from the turbine (and not closer to the turbine, e.g., 0.5–1 D), which suggests that the rolling moment is more influenced by horizontal shear in the flow than by wake rotation.

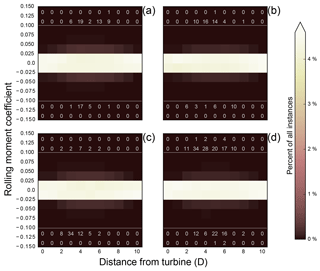
Figure 5 Two-dimensional histograms of all calculations of rolling moment coefficient experienced by all aircraft in the neutral (a, b) and stable (c, d) cases for down-wake (a, c) and cross-wake (b, d) transects as a function of the downwind distance from the turbine (in rotor diameters D). “Non-low” hazards ($\left|C_{\mathrm{roll}}\right|\mathit{>}\mathrm{0.1}$) are explicitly totalled in their respective bins.

4 Discussion and conclusion

As wind energy development increases in the vicinity of general aviation airports, concerns for turbine-wake-induced roll hazards on aircraft grow. Of particular concern is the rolling moment, the aerodynamic force applied at a distance from an aircraft's center of mass that causes the aircraft to undergo angular acceleration about its roll axis. Using LES of stable and neutral flow past a utility-scale wind turbine, we quantify the roll hazards experienced by general aviation aircraft transecting the wake.

We represent a typical general aviation aircraft in the LES data as a 10 m line comprised of eight segments that are 1.25 m in length. At each point along the aircraft, we sample the LES wind vectors to calculate rolling moment and the rolling moment coefficient. We define 540 flight tracks to march through the wake to make the roll hazard calculations. The flight tracks have down-wake and cross-wake orientations and extend through the entire downwind 682 points and 247 points, respectively, yielding 176 880 calculations of a roll hazard for each stability case for each time step of data.

The rolling moment coefficient serves as our primary roll hazard metric, as it normalizes the rolling moment on the aircraft by the aircraft size, shape, and airspeed to produce a standard hazard index. This index has been classified by past studies into thresholds for low, medium, and high roll hazards. When comparing a sample flight path outside of the wake's influence to one within the wake center, we find that an aircraft flying within the wake experiences higher rolling moment coefficient than an aircraft flying in a wake-free environment. However, analyses of all 540 flight paths through the wake reveal that over 99.99 % of hazard calculations remained within the low criterion in both neutrally stratified and stably stratified conditions across 100 s of data. In neutral conditions, the largest of these hazards are classified as medium hazards and exist 6.5 D downwind of the turbine in the bottom-left portion of the rotor disk. The highest hazards in the stable case also remained within the medium threshold and are located in two separate regions of the wake: approximately 4 D downwind in the bottom-right quadrant of the rotor and 6 D downwind in the top-left quadrant of the rotor.

Our calculated roll hazards differ from those in Mulinazzi and Zheng (2014), who used a helical vortex model scaled up from wind tunnel measurements to find significant roll hazards far downwind from a wind turbine. Conversely, our results using an actuator-line representation of a wind turbine in the SOWFA LES model rarely surpass the low roll hazard threshold. Rather, our results agree with those of Wang et al. (2015, 2017), whose calculations are computed from the Beddoes circulation formula (Madsen and Rasmussen, 2004), as opposed to the wind tunnel extrapolation in Mulinazzi and Zheng (2014). Past successes in turbine wake modeling using LES actuator-line methods can in part validate our results (e.g., Churchfield et al., 2012; Jha et al., 2015; Nilsson et al., 2015).

This study presents a simple method for quantifying turbine-wake-induced roll hazards on general aviation aircraft and is constrained by the assumptions made to represent an aircraft within LES data of a single turbine wake. While we have shown that individual wakes in neutrally stratified and stably stratified conditions are unlikely to pose hazards to general aviation aircraft, interactions between wakes could also be explored. Future simulations of wind plants that allow for wake interaction (as in Vanderwende et al., 2016) and larger turbine types could be useful. Our conclusions are drawn from rolling moment calculations, though additional calculations of yawing and pitching moments could also be beneficial. Our results may also be supported by field tests, in which tethersondes (Lundquist and Bariteau, 2015) or unmanned aircraft vehicles (Baserud et al., 2014; Kocer et al., 2012; Lawrence and Balsley, 2013) would fly through the wake of a real utility-scale turbine during variable conditions to directly measure roll hazards. Future studies could integrate simulations like these with flight simulators to understand the coupling of the atmospheric behavior to pilot response for an integrated assessment of roll hazard, as in Wang et al. (2015).