Full-scale wind turbine performance assessment: a customised, sensor-augmented aeroelastic modelling approach

Blade erosion of wind turbines causes significant performance degradation, impairs aerodynamic efficiency, and reduces power production. However, traditional monitoring systems based on supervisory control and data acquisition (SCADA) data, which rely on operational data from turbines, lack effectiveness at early detection and quantification of these losses. This research builds on an established turbine performance integral (TPI) method with a sensor-augmented aeroelastic modelling approach to enhance wind turbine performance assessment, focusing on blade erosion. Applying this approach to a distinct multi-megawatt turbine model, the study integrates multibody aeroelastic simulations and real-world operational data analysis. The study identified readily available sensors that were sensitive to blade surface roughness changes caused by erosion. Operational data analysis of offshore wind turbines validated the initial sensor selection and approach. Refined simulations using further virtual sensors quantified the effect size of these sensors' output under different turbulence levels and blade states, employing Cohen's d – a dimensionless metric measuring the standardised difference between two means. For the turbine investigated, findings indicate that sensors such as blade tip torsion, blade root flap moment, shaft moment, and tower moments, especially under lower turbulence intensities, are particularly sensitive to erosion. This confirms the need for turbine-specific, controller-informed sensor selection and emphasises the limitations of generic solutions. This research provides an approach for bridging simulation insights with operational data for turbine-specific performance assessment, contributing to the development of condition monitoring systems (CMSs), resilient turbine designs, and maintenance strategies tailored to specific operating conditions.

1 Introduction

Wind energy has emerged as a cornerstone of the global transition towards sustainable power generation, offering a renewable source that aligns with environmental responsibility and economic feasibility. Central to the operational integrity and efficiency of wind turbines are their blades, whose performance is significantly impacted by the condition of their leading edges. Environmental factors coupled with high tip speeds subject these blades to erosion and surface roughening, which reduces the aerodynamic efficiency and thereby decreases their annual energy production (AEP) (Han et al., 2018; Maniaci et al., 2016; Bak et al., 2020; Bak, 2022). It is well-understood that even minor surface imperfections can have profound consequences, adversely affecting performance by altering the blade's aerodynamic profile. This phenomenon necessitates a deeper understanding of how blade erosion impacts wind turbine efficiency, with the aim of developing more resilient blade designs and maintenance strategies to optimise output and enhance turbine longevity. Therefore, a comprehensive understanding of the impact of blade erosion on wind turbine efficiency is crucial.

The precise quantification of performance changes caused by blade erosion and subsequent repairs has received considerable attention in wind energy research. Investigations, such as those outlined by Malik and Bak (2024b), have illuminated the complex relationships between blade surface condition, aerodynamics, operational dynamics, and turbine efficiency. This research builds upon those findings and further explores a refined analytical approach that emphasises the nuances of varying turbine control systems. By integrating multibody aeroelastic simulations for performance data analysis, this study aims to provide a more detailed understanding. A key aspect of this investigation is the use of turbine-generated supervisory control and data acquisition (SCADA) data for performance monitoring. While the value of SCADA data in this context is well-established (Ding et al., 2022; Yang et al., 2014; Badihi et al., 2022; Gonzalez et al., 2019; Butler et al., 2013), it has become evident that existing sensor configurations have limitations. This highlights a pressing need for adaptable monitoring strategies tailored to the specific characteristics of each turbine model and its control system, as emphasised by Malik and Bak (2024b). In contrast to methodologies that generalise sensor pair applications across different original-equipment manufacturer (OEM) turbine models, this work emphasises the deliberate selection of a controller-specific sensor pair. For instance, using power as a function of generator speed or power as a function of wind speed indiscriminately across turbines can overlook critical differences in turbine dynamics and control strategies. This strategy emphasises the importance of finding the most suitable sensor pairings for each turbine and associated controller philosophy.

The primary motivation for the preliminary investigation was to determine whether the sensors readily available to wind farm owners and operators via SCADA systems could effectively track individual wind turbine performance and, more specifically, the reduction in power output due to erosion. The question is whether sensors exist in the real world that can detect possible reductions in power output, even amidst the unsteady signals present in SCADA data analysis. This study begins with preliminary multibody aeroelastic simulations, using an OEM-provided proprietary model that matches the operational turbines under investigation, and features a focus on rudimentary but widely accessible sensors since there is often a limited sensor array available in SCADA systems (Leahy et al., 2019; Yang et al., 2014). The initial simulations focus on identifying the correct and effective sensor pairs for the turbine and its controller that exhibit significant sensitivity to blade erosion, setting the foundation for the development of a turbine-specific turbine performance integral (TPI). This approach recognises that while more advanced sensors may be available to OEMs or may be potentially deployable in future turbine designs, it is imperative to first understand the capabilities of the existing sensor configuration. This prioritisation aims to ensure that the findings are relevant and can used to improve current wind turbine performance monitoring systems. Guided by these simulation insights, the work then analyses a unique dataset covering 16 horizontal-axis three-bladed multi-megawatt turbines within the same offshore wind farm, with nominal power between 3 and 4 MW and with an approximate average wind speed of 9.49 m s⁻¹. With this knowledge, the corresponding Reynolds number, Re, can be determined by the rule of thumb (Bak, 2023), where Re is proportional to the radius, R, of the rotor and between 75 000⋅R and 150 000⋅R. Thus, Re is approximately 7 million. Importantly, some of these turbines were commissioned with leading-edge protection (LEP), while others were not, providing a valuable comparison point for erosion effects. Spanning January 2015 to November 2023, this dataset allows for longitudinal investigation of performance changes due to blade erosion, the staggered application of LEP, and blade repairs, as well as other events in the turbine's history.

Building upon the author's previous analysis (Malik and Bak, 2024b) of wind turbine SCADA data to detect performance impacts due to various influences such as erosion, this study extends the analysis to include a distinct turbine model from a different OEM, while continuing to investigate seasonal impacts, long-term trends, and blade erosion's effects. The turbine performance integral (TPI) methodology introduced in the previous study is employed. This provides additional support for the approach of STL (seasonal and trend decomposition using LOESS, where LOESS stands for “locally estimated scatterplot smoothing”) (Cleveland et al., 1990) for turbine performance assessment but also explores its applicability to the inclusion of a turbine from an alternative OEM. Importantly, the sensor pairs used in this work are distinct from those in the authors' previous publication and are specifically aligned with the current turbine model and control system under investigation. Furthermore, this study employs the turbines' nacelle-mounted anemometers, despite their inherent measurement uncertainties as highlighted in the IEC 61400-12-2:2013 (International Electrotechnical Commission, 2013) and IEC 61400-12-1 (International Electrotechnical Commission, 2017) standards, which recommend wind speed measurements 2.5 rotor diameters upstream of the turbine at various heights. This study avoids the use of separate meteorological masts and explores the possibility of monitoring individual turbine performance trajectories, using the metrics of either power as a function of wind speed (measured by the turbine anemometer) or generator RPMs (rotations per minute) as a function of wind speed.

The “refined” simulation study, while more aspirational in nature, expands the investigation to a broader range of sensors, including those not currently available to owners but potentially accessible to OEMs, as well as conceptual future sensors. This approach utilises multibody simulations to evaluate a wide range of virtual sensors, identifying those with heightened sensitivity to the efficiency changes caused by blade erosion. Simulation scenarios are designed to evaluate turbine responses under various conditions, focusing on wind speeds, turbulence intensities, and blade condition. This approach, utilising theoretical models, aims to refine sensor selection methodologies and to advance the understanding of wind turbine performance dynamics. Additionally, it aims to provide understanding that may inform future research directions in turbine monitoring and maintenance strategies.

This study integrates multibody simulation and SCADA measurement analysis, emphasising the necessity of a turbine-specific, controller-informed approach to monitoring turbine performance changes, as opposed to generalised methodologies. The findings highlight the benefits of strategically selected and deployed sensors, informed by proprietary-control philosophies. This research intends to encourage collaboration between academics, turbine manufacturers, and operators to implement data-driven strategies for enhancing turbine performance monitoring.

2 Method

2.1 Preliminary multibody simulations for sensor pair identification

The study's initial phase employed the blade-element-momentum-based (BEM-based) multibody aero–servo–elastic tool HAWC2 (Horizontal Axis Wind turbine simulation Code, 2nd generation), developed by DTU Wind Denmark (Larsen and Hansen, 2007), to identify sensor pairs that are potentially sensitive to the performance changes caused by blade erosion. The focus of the preliminary investigation is on sensors that are readily available via SCADA systems. This exploration is predicated on the hypothesis that certain sensor pairs, when analysed under simulated erosion conditions, may provide indications of performance decline. The selection of sensors, specifically, pitch, generator RPMs, and power as functions of wind speed, is informed by the turbine- and by OEM-specific proprietary-controller settings. This tailored approach, which explicitly considers controller dynamics, represents a departure from methodologies that do not account for these factors.

This work builds upon the authors' previous findings (Malik and Bak, 2024a) by combining multibody aeroelastic simulations and real-world operational data analysis, thus addressing the gap between simulation-based findings and empirical validation. The previous study focused solely on the simulated environment, investigating the combined effects of leading-edge erosion and turbulence intensity (TI), as well as exploring time-interval averaging as a data processing technique. To assess the feasibility of observing the power degradation in real-world measurements, that study compared the performance of turbines with clean blades to those with simulated surface roughening.

This study uses the same OEM-provided certified multibody model of an operational turbine's controller in the full aero–servo–elastic simulation loop, ensuring the accurate capture of the response to degraded blades, including pitch adjustments utilising aerodynamic reserves. Furthermore, the previous study advocated for the use of higher-resolution data in analyses to improve the detection of subtle performance changes, a recommendation that this current study implements by utilising 1 s sampled rather than 10 min averaged data. For a more detailed elaboration of the methodology employed and implications for this work, readers may refer to the aforementioned paper.

Furthermore, in this work the effectiveness of the identified sensor pairs for the turbine investigated is compared to that found in previous research (Malik and Bak, 2024b), where a distinct wind turbine from a different OEM was studied and for which the relationship of generator speed as a function of power formed the basis for the monitoring of performance variation over time using the turbine performance integral (TPI). This cross-turbine sensor comparison reinforces the importance of tailoring sensor selection to specific turbine models and control systems. Furthermore, the application of the TPI method for the turbine under investigation demonstrates the method's applicability across diverse wind turbine designs. These elements of the study contribute to a better understanding of performance monitoring across varied wind turbine configurations.

2.1.1 Modelling leading-edge erosion

To model blade-leading-edge erosion, surface roughness based on wind tunnel tests from Krog Kruse et al. (2021) is used. These tests utilised P400 (fine-grit) and P40 (coarse-grit) sandpaper to simulate different erosion levels on an alternate aerofoil and provided the empirical basis for deriving factors for the blade modifications. To simulate early-stage degradation, the outer 15 % of the blade model's original aerofoil polars are altered by applying a factor of 0.9 to the clean aerofoil polar and scaling the drag polar by factors of 1.5 (P400) and 2.0 (P40) (see Malik and Bak, 2024a, for details) to reflect the erosion observed after approximately 2 years of operation. It is important to note that this study employs a simplified approach relying on relative changes, and the simulated roughness may differ from the actual turbine's conditions. Therefore, while these simulations reflect deteriorating changes in blade conditions, they do not necessarily represent the precise changes that occur in real-world scenarios.

2.1.2 Simulation settings and test cases

To analyse the impacts of turbulence intensity and blade erosion on wind turbine performance, simulations were conducted using an OEM-provided multibody model representing the operational offshore wind turbine also investigated as part of this work. Simulations were performed for one clean and two blade-leading-edge-erosion states across a range of turbulence intensities, with further model parameters and conditions provided in Malik and Bak (2024a). In contrast to the previous work where simulations were run at 1 m s⁻¹ increments, the current study employs a higher-fidelity approach. To focus on the turbine's power ramp-up phase (where erosion effects are most likely to manifest) and to ensure that the binning and averaging process of the data did not obscure subtle dynamics, individual cases were run in 0.1 m s⁻¹ increments between 6.5 and 14 m s⁻¹. This increment achieves a balance between fine-scale accuracy and computational efficiency. Following the IEC (2019) 61400-1 standard, six individual simulation runs, or seeds, were used per configuration to ensure statistical robustness.

Turbulence intensity (TI) was varied across a spectrum (0 %, 3 %, 6 %, 9 %, and 12 %), with 6 % approximating filtered average offshore conditions. Simulations were executed for 900 s, with data from the last 600 s analysed to ensure steady-state conditions. Time steps were set at 0.01 s. Wind shear followed a power-law profile with an alpha value of 0.14, and air density was fixed at 1.225 kg m⁻³ (representative of sea-level conditions at 15 °C). The default Mann turbulence model parameter, $\mathit{\alpha }{\mathit{ϵ}}^{\mathrm{2}/\mathrm{3}}$, of 1 was used (Mann, 1994). For detailed explanations, please refer to the HAWC2 manual (Larsen and Hansen, 2007) and IEC61400-1 edn. 3 (IEC, 2019).

With the focus of the preliminary investigation on sensors that are readily available via SCADA systems, simulations utilising the multibody aeroelastic model facilitated the identification of sensor pairs that exhibit significant sensitivity to blade erosion, setting the foundation for the development of a turbine-specific turbine performance integral (TPI). Due to confidentiality agreements, a generalised description of the turbine is provided, and results are presented in relative terms.

2.2 Wind turbine operational SCADA data analysis

Building upon the sensor pairs identified through multibody simulations, this section conducts an analysis of SCADA data from operational turbines. By focusing on the sensor pairs of power as a function of wind speed and generator RPMs as a function of wind speed, this investigation aims to validate the simulation-derived hypotheses within a real-world setting, assessing their feasibility and effectiveness at detecting blade erosion. This analysis both tests the hypotheses generated from the simulations and provides a practical process for evaluating the sensor pairs' effectiveness at performance monitoring.

For this purpose, 16 front-row, offshore multi-megawatt turbines within the same wind farm were selected for their direct exposure to dominant wind conditions. Due to confidentiality agreements, the specific site and turbine type will not be disclosed. The wind farm provides an extensive SCADA dataset spanning January 2015 to November 2023. This dataset offers a valuable experimental timeline, with some turbines installed with a specific LEP (type A), while others remained unprotected. As expected, unprotected blades exhibited significantly greater erosion within the first 2 years of operation. Starting in 2019, remedial actions were taken, i.e. the repair of unprotected blades and the application of a different shell-type LEP system (type B). This application was phased, with some turbines receiving partial LEP coverage (approximately 7 %–8 % of the blade span) and others receiving complete coverage (15 %). Notably, LEP application could take from a week up to, in exceptional cases, a month, due to logistical arrangements in an offshore environment. In 2021, the remaining turbines received full LEP coverage. Additionally, minor LEP repairs (approximately 0.5–1.5 m) were performed in 2020 and 2021; however, these lesser interventions are not expected to produce a measurable impact on turbine performance. This dataset, with its distinct phases of LEP application and repair, provides an opportunity to investigate the longitudinal effects of blade erosion and the impact of the application of LEP, or change in the aerodynamic profile, on wind turbine performance. Data regarding LEP applications and repairs were obtained directly from technician reports.

From the restricted set of sensors accessible through the SCADA system, the following parameters pertinent to the investigation were gathered:

• nacelle wind speed ν (m s⁻¹),

• nacelle direction (°),

• ambient temperature T (°C),

• blade pitch angle β(°),

• generator speed Ω (RPMs),

• power production P (kW),

• power set point demand P (kW), and

• turbine operational state (e.g. waiting for wind, curtailed, cable unwind, etc.).

To heighten the accuracy of detecting subtle performance changes (Badihi et al., 2022; Malik and Bak, 2024a), this study utilised a dataset comprising SCADA data sampled at 1 s intervals (rather than 10 min averaged data), which were pre-computed from the wind turbine's data archive, where a sensor's signal is only updated when a change is recorded. Missing values were handled using the “previous value” method to reduce computational demands. The dataset was filtered and processed according to International Electrotechnical Commission (IEC) 61400-12-1 guidelines International Electrotechnical Commission (2017) but not corrected for temporal density variations. Nacelle direction served as a proxy for wind direction, despite being influenced by the turbine's control algorithm hysteresis and rotor wake.

2.2.1 Wind turbine control and turbine performance integral

An understanding of the characteristics of the turbine investigated reveals that the turbine employed in this study contrasts with the previous work where the TPI method was first introduced (Malik and Bak, 2024b), such that the rotor control does not primarily rely on its wind speed anemometer as a control input during its power generation mode. Once it is generating power, the turbine controller relies on operational trajectories following a speed–power and a pitch–power curve rather than using direct information regarding the wind speed. Examples of such control include work by Hansen and Henriksen (2013).

For the turbine investigated, the turbine performance integral (TPI) is defined as the area under the power curve between wind speeds of 6 and 10.5 m s⁻¹. This integral, with units of power ⋅ wind speed (kW m s⁻¹), is used to extract the seasonal variations using the STL technique that serves as an indicator of the turbine's performance trajectory. Alternatively, the generator RPMs as a function of wind speed area metric (between 5.5 and 8.5 m s⁻¹) may be employed. It is important to ensure that the wind speed limits selected create a monotonic relationship and that the turbine operates outside of full-load conditions. This is because the effects of erosion are primarily visible in partial-load conditions. The pitch angle–wind speed relationship only becomes monotonic between 10.5 and 11.5 m s⁻¹, making it less suitable.

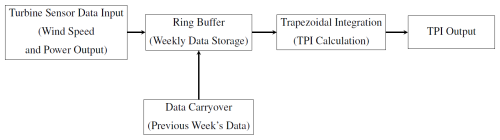
A weekly updating ring buffer with a fixed value is employed, the adjustment of which affects TPI outcomes. The structure and data flow of the ring buffer system can be visualised in Fig. 1. This block diagram illustrates how sensor data (in this case, power and wind speed output) are input to the system, stored in a ring buffer, and processed through bin-wise trapezoidal integration to compute the TPI. Additionally, the diagram shows the data carryover mechanism, where the previous week's data are used to fill gaps when insufficient new data are available.

Figure 1 Block diagram of the ring buffer system for wind turbine performance monitoring.

The ring buffer’s mathematical model is based on modular arithmetic, which facilitates its circular structure. Let B represent the buffer size, i_current the current index for data entry, and t_n the nth data point from the sensors. The position for the next data point is determined by

$$\begin{array}{}\text{(1)}& i_{\text{next}}=(i_{\text{current}}+\mathrm{1})\mathrm{mod}B.\end{array}$$

This equation ensures that when the buffer reaches its capacity, it wraps around and starts overwriting the oldest data. The buffer size affects how quickly changes are detected. A large buffer may smooth out short-term variations, while a smaller buffer is more responsive to immediate fluctuations.

Once the data are stored in the buffer, the TPI is calculated using trapezoidal integration. TPI quantifies turbine efficiency by representing the area between the power (P) as a function of wind speed (v) and the wind speed axis over a specified range. Mathematically, the TPI is defined as

$$\begin{array}{}\text{(2)}& \text{TPI}=\underset{v_{\mathrm{1}}}{\overset{v_{\mathrm{2}}}{\int }}P\left(v\right),\mathrm{d}v.\end{array}$$

This integral calculates the area under the power curve between power levels v₁ and v₂, which correspond to 6 and 10.5 m s⁻¹, respectively, providing a measure of turbine performance within this operational range.

2.2.2 Seasonal-trend decomposition and data visualisation

An analysis of wind turbine SCADA data is used to assess the influence of seasonal effects and blade erosion on performance. This study utilises the approach employed in Malik and Bak (2024b), where the turbine performance integral was first introduced. The TPI signal is used to extract the seasonal variations using the seasonal and trend decomposition using LOESS (STL) method (Cleveland et al., 1990). The STL technique decomposes a time series into three components: seasonal, trend, and residual. This decomposition is mathematically represented as follows:

$$\begin{array}{}\text{(3)}& Y_t=T_t+S_t+R_t,\end{array}$$

where Y_t denotes the observed data at time t, T_t is the underlying performance trend component, S_t is the cyclical seasonal component related to annual variations in atmospheric conditions, and R_t is the residual component that is composed of un-attributed transient factors.

This work focuses on the direct impact of LEP applications and repairs on long-term performance trends. Rather than attempting to isolate the various factors influencing performance, as was done in the previous study, this work overlays data regarding LEP applications and repairs onto the long-term performance trajectory. This approach acknowledges the limitations of this approach in providing a comprehensive picture but attempts to offer insights into the direct effects of these interventions. A multi-panel visualisation with a shared time axis is employed to analyse wind turbine performance data decomposed using STL, which was performed using MATLAB's “trenddecomp” function (The MathWorks, Inc., 2023). This approach allows for the simultaneous examination of long-term trends and seasonal and remainder components, highlighting their interactions over time. The shared temporal axis serves as a reference point to compare the evolution of each component, aiding the identification of changes and potential anomalies within the data.

While previous work (Malik and Bak, 2024b) emphasised the meticulous collection of operations and maintenance (O&M) data, including detailed accounts of events that included blade erosion and repair-related interventions, the current investigation adopts a more focused approach. This decision does not diminish the significance of O&M activities on turbine performance. Instead, it aligns the scope with the specific objective of validating and applying the TPI method. This approach provides an illustration of the method's capabilities within the context of a distinct OEM model and control system rather than constituting a comprehensive analysis of O&M's influence on turbine performance.

2.3 Refined multibody simulations for detailed sensor evaluation

Building upon the empirical validation of initial findings, this research advances to a series of multibody simulations designed to gain a deeper understanding of various sensors' sensitivity to blade erosion under varied turbulence intensity conditions. Details of the simulation methodology may be found in Sect. 2.1, where the preliminary investigation is described.

The primary objective of this exercise is to evaluate a diverse array of sensors chosen based on their potential to detect changes in blade aerodynamic performance due to erosion. While a wider selection of sensors was simulated, including lift and drag coefficients at various blade positions, the sensors displayed were down-selected based on the following criteria:

• Relevance to blade aerodynamic performance. Sensors that directly or indirectly measure parameters influenced by changes in blade surface conditions, such as blade loads, power output, and moments, are prioritised.

• Availability in existing SCADA or condition monitoring systems (CMSs). Sensors that are commonly available or can be readily integrated into current monitoring systems are preferred to facilitate practical implementation in real-world scenarios.

• Sensitivity to erosion-induced changes. Sensors that exhibit a clear and measurable response to varying levels of blade erosion are selected to ensure reliable detection.

• Signal-to-noise ratio. Sensors with high signal-to-noise ratios are chosen to minimise the influence of external factors and measurement uncertainties.

While the findings for these sensors may be specific to the turbine studied, the process serves as an example of a procedure that may be followed for other turbines. This evaluation begins with selecting a broader range of virtual sensors within the simulation environment to identify suitable indicators of erosion-related performance changes. These sensors include but are not limited to blade root bending moments, blade tip deflections, tower top and bottom loads, and drivetrain torque. The selection criteria prioritise sensors or data channels that are readily deployable and practical in real-world scenarios and have the potential to improve existing monitoring and performance analysis capabilities.

Next, a series of multibody simulations are conducted, modelling the turbine under various operating conditions. The sensors selected are subjected to a series of simulations under various blade erosion states (clean, P400, and P40) and turbulence intensity conditions (0 %, 3 %, 6 %, 9 %, and 12 %). The response of the generated sensors is then processed and analysed using Cohen's d (described in detail in Sect. 2.3.1) to quantify the effect size of blade erosion on each sensor's output. Sensors exhibiting high sensitivity are identified as potential candidates for erosion detection and performance monitoring. The understanding gained from the simulation results are then discussed in terms their relevance and practical application.

The methodology explores theoretical simulation but stops short of the empirical validation that would ensure that the findings are anchored in both theoretical rigour and operational relevance, due to the nonexistence of or a lack of access to the broader sensor suite in the real world. This exercise, however, demonstrates the potential of such sensors in revealing valuable information regarding turbine performance and suggests their inclusion in future turbine designs, which is a key motivation of this study. Despite this, the results are discussed for their practical applicability. This simulation-based methodology aims to complement traditional SCADA data analyses, providing perspectives that might be difficult to glean from operational turbines alone, while simultaneously highlighting the need for development in sensor deployment in wind turbines to improve performance monitoring and maintenance strategies.

2.3.1 Framework for sensor output comparison – Cohen's d calculation

This study quantifies the impact of erosion through differences in sensor output, providing visualisations of both clean and eroded blade states. The primary objectives are to gain an understanding of turbine performance dynamics and to contribute to the development of monitoring strategies for early detection of erosion or performance deviations.

To compare multiple sensor outputs under different blade conditions, an appropriate statistical metric is needed. Cohen's d (Cohen, 1992) was chosen due to its ability to quantify effect size. It provides a standardised measure of the difference between two means that is independent of the units of measurement. This allows for meaningful comparisons across diverse sensor outputs (e.g. blade root bending moment or tower moment as functions of wind speed).

Importantly, Cohen's d provides a normalised measure of effect size. This is valuable for understanding the magnitude of erosion's impact and for identifying the sensors that are most sensitive to changes in blade aerodynamic surface properties. Using a percentage change for this comparison would disproportionately emphasise changes in values close to zero, whereas Cohen's d avoids this potential bias.

Cohen's d was applied in an analysis of full-scale measurements (Malik and Bak, 2024b) and serves as the link between the simulations and future full-scale measurements. Using this method will indicate whether certain signals can be detected better than others.

To quantify the difference between clean and rough (P40) blade conditions for each sensor and wind speed bin, Cohen's d was calculated:

$$\begin{array}{}\text{(4)}& d={\displaystyle \frac{{\stackrel{\mathrm{‾}}{x}}_{\mathrm{rough}}-{\stackrel{\mathrm{‾}}{x}}_{\mathrm{clean}}}{s_{\mathrm{p}}}},\end{array}$$

where d is Cohen's d (a dimensionless measure of effect size), ${\stackrel{\mathrm{‾}}{x}}_{\mathrm{rough}}$ is the mean of the sensor data in the rough blade condition, ${\stackrel{\mathrm{‾}}{x}}_{\mathrm{clean}}$ is the mean of the sensor data in the clean blade condition, and s_p is the pooled standard deviation calculated as

$$\begin{array}{}\text{(5)}& s_{\mathrm{p}}=\sqrt{{\displaystyle \frac{(n_{\mathrm{rough}}-\mathrm{1})s_{\mathrm{rough}}^{\mathrm{2}}+(n_{\mathrm{clean}}-\mathrm{1})s_{\mathrm{clean}}^{\mathrm{2}}}{n_{\mathrm{rough}}+n_{\mathrm{clean}}-\mathrm{2}}}},\end{array}$$

where n_rough is the number of samples in the rough condition, n_clean is the number of samples in the clean condition, s_rough is the standard deviation of the sensor data in the rough condition, and s_clean is the standard deviation of the sensor data in the clean condition.

The magnitude of Cohen's d aids in interpreting the practical significance of the differences observed between clean and rough blade conditions. Values around 0.2 indicate a small effect size, 0.5 a medium effect, and 0.8 or greater suggests a large effect. However, these values should be interpreted as a guide that should be informed by the context of the relevant sensor in context of this analysis (Cohen, 1992). This allows for the identification of the most-erosion-sensitive sensors and the assessment of the impact's magnitude.

Furthermore, this metric is appropriate for this work, as it incorporates a pooled standard deviation. This accounts for potential variability in the number of data points across simulations and sensors, ensuring valid comparisons.

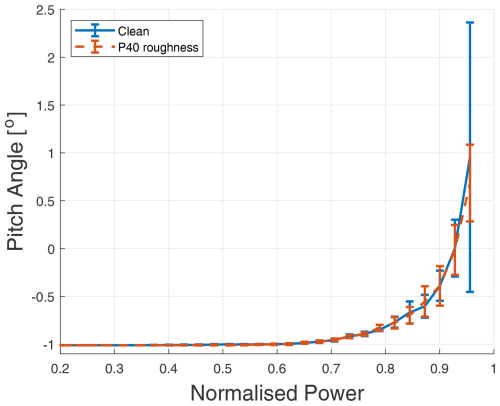
Figure 2 Blade pitch angle as a function of normalised power for clean and rough blade profiles, with a fixed turbulence intensity of 6 % (simulated).

Figure 3 Normalised generator speed as a function of normalised power for clean and rough blade profiles, with a fixed turbulence intensity of 6 % (simulated).

3 Results and discussion

3.1 Preliminary multibody simulations for sensor pair identification

The comparative analysis revealed substantial behavioural differences between sensor pairs, attributable to the varying turbine control systems. For the turbine investigated in this study, illustrated in Figs. 2 and 3, the relationships between blade pitch angle and generator speed as functions of normalised power did not exhibit any noticeable changes due to alterations in blade roughness (error bars represent 1 standard deviation). This finding contrasts sharply with the sensor pair dynamics of the turbine evaluated in Malik and Bak (2024b), where this specific sensor pair formed the basis of the TPI signal.

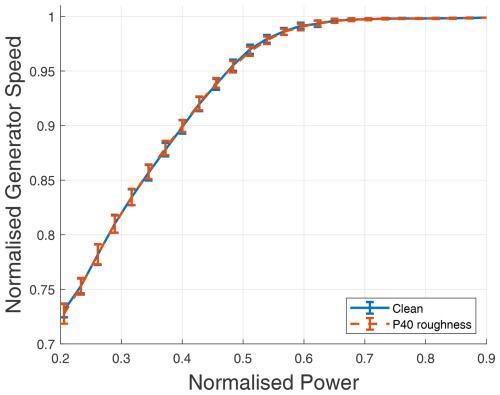
However, Figs. 4 and 5 demonstrate that erosion at the leading edge significantly affects turbine performance. In the former, an eroded blade necessitates more aggressive pitching to sustain power generation, while in the latter, an eroded blade manifests in lower RPMs for any given wind speed. This suggests a shift in operational set points, given that the turbine's control algorithm does not incorporate wind speed measurements from its anemometer during production.

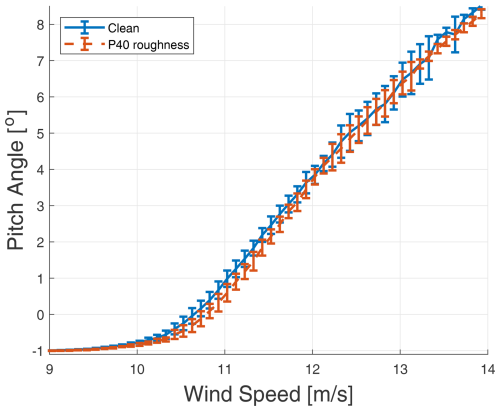
Figure 4 Blade pitch angle as a function of wind speed for clean and rough blade profiles, with a fixed turbulence intensity of 6 % (simulated).

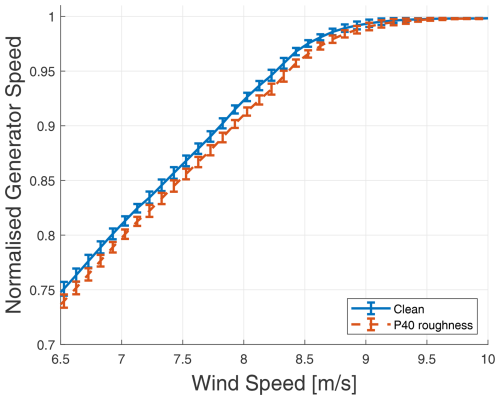
Figure 5 Normalised generator speed as a function of wind speed for clean and rough blade profiles, with a fixed turbulence intensity of 6 % (simulated).

These results highlight the necessity of a turbine-specific approach in selecting sensor pairs to effectively assess turbine performance. A generic, one-size-fits-all strategy is inadequate for addressing the complexities of diverse turbine control philosophies. Thus, it is necessary to develop tailored sensor pair selection methods to ensure the accuracy of performance integrity evaluations.

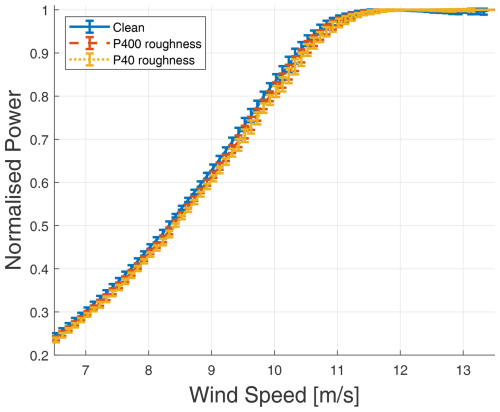
Figure 6 Normalised power as a function of wind speed for various blade profiles, with a fixed turbulence intensity of 6 % (simulated).

Furthermore, shown in Fig. 6 is the normalised power curve for three blade profiles. These simulations are executed at 6 % TI, which approximates the mean annual turbulence intensity at the location of the real offshore turbines analysed later in this study. The simulation results demonstrate that the roughening of the blade leading edge has a detrimental impact on the turbine performance. The area under this normalised power curve, specifically between wind speeds of 6 and 10.5 m s⁻¹, will form the foundation of the turbine performance integral (TPI) signal. In this manner, the TPI signal encapsulates the variations in power output due to blade surface conditions. It offers a quantifiable metric to assess the degree of erosion's impact on turbine efficiency.

3.2 Wind turbine operational SCADA data analysis

Building upon the authors' previous work (Malik and Bak, 2024b), which attempted to correlate turbine performance with operations and maintenance (O&M) events, this study adopts a more focused approach. Recognising the considerable resource investment required to compile comprehensive O&M datasets, particularly those pertaining to blade erosion and repair-related interventions, this investigation focuses on demonstrating the application of the TPI method. This deliberate focus allows further examination of the decomposition technique for assessing turbine performance and expands the approach to incorporate a turbine from a different OEM. Thus, it connects the findings of the previous work (Malik and Bak, 2024b) with the focused investigations of the current paper.

Presented in Fig. 7 is the measured power curve for the turbine in question, with the variability indicated by the standard deviation bars. This dataset spans approximately 9 years. For this graphical representation, 10 min averaged data were utilised, whereas all other measurement analyses utilise non-time-averaged 1 s sampled data. The data were filtered and processed in adherence with the standards prescribed in the IEC 61400-12-1 (International Electrotechnical Commission, 2017). This 10 min averaging allows for a direct visual comparison with the simulated power curve shown earlier in Fig. 6. Variation between the profiles of the two curves may be attributed to an array of influences, including the fidelity of data filtering, temporal changes in turbine performance, fluctuating atmospheric conditions, and the impact of O&M interventions.

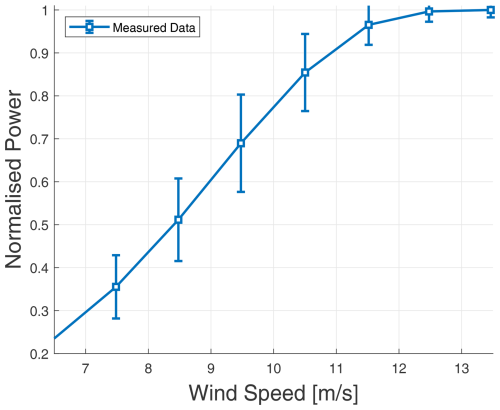
Figure 7 Power as a function of wind speed (filtered dataset, 10 min averaged, measured). Error bars represent 1 standard deviation from the mean.

3.2.1 Seasonal-trend decomposition

The seasonal-trend decomposition analysis of the TPI signal performed in this study expands upon the methodologies and findings presented in Malik and Bak (2024b). While the general approach to decomposing turbine performance data into trend, seasonal, and residual components remains consistent, the current investigation introduces a detailed examination tailored to the unique operational characteristics and sensor configurations of the turbine under investigation. The focus of this analysis is the extension of the previously introduced methodology, paired with a turbine and controller-specific sensor pair (i.e. power as a function of wind speed based on simulation-based results; see Sect. 3.1).

Figure 8 illustrates the trend decomposition of one of the 16 turbines under investigation. This figure illustrates the decomposition of a single turbine’s performance, highlighting the long-term performance improvement or decline, the recurrent seasonal patterns, and the short-term deviations from expected performance trends. Here, an increased trend reflects improved turbine performance, and the opposite is true for a reduction in trend trajectory. These changes may be caused by operational and maintenance events, blade repair, erosion, or various other factors. The seasonal component illustrates the cyclical performance variations attributable to environmental factors. It is worth noting that the analysis methodology has been applied to scenarios including waked turbines, yielding consistently sound results despite the potential for additional variability under those conditions. Importantly, the TPI signal relies exclusively on data generated by the individual turbine, without incorporating comparisons to neighbouring turbines or meteorological masts.

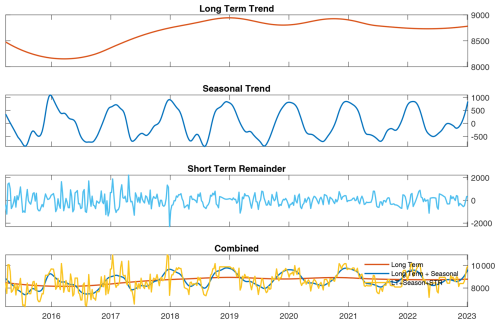
Figure 8 Decomposition of a single turbine's performance trends over 9 years, with power as a function of wind speed. Vertical scales represent the turbine performance integral (TPI) in units of power ⋅ wind speed (kW m s⁻¹).

To highlight the important role of sensor pair selection, consider the power-to-wind-speed TPI signal. This signal is a more responsive indicator for detecting performance oscillations, which is empirically substantiated here. Figure 9 elucidates the comparative dynamics of TPI signals extracted using two distinct sensor pairs: power as a function of wind speed and generator speed as a function of power. The normalisation process, involving the division of the seasonal-trend component by the long-term trend component, provides a dimensionless metric encapsulating temporal performance variations. The power-to-wind-speed TPI signal exhibits pronounced cyclicality, reflecting substantial seasonal performance fluctuations, demonstrating its higher sensitivity to performance oscillations. Conversely, the generator-speed-to-power TPI signal demonstrates notably muted cyclical behaviour, largely due to the turbine's generator speed adhering to a pre-encoded operational “ceiling” (see Fig. 2). This programmed limit delineates the maximum-permissible generator speed relative to power, preventing upward deviations.

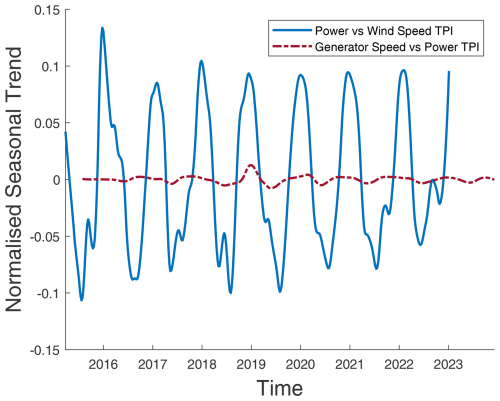
Figure 9 Comparison of normalised seasonal trends in the turbine performance integral (TPI) over time for two sensor pairs: power as a function of wind speed and generator RPMs as a function of wind speed. The vertical axis represents the TPI, with values normalised to highlight relative changes. This comparison demonstrates the higher sensitivity of the power as a function of the wind speed pair.

3.2.2 Seasonal influence

Presented in Fig. 10 are the aggregated seasonal trends of the turbines investigated, highlighting variations that may not be evident from the analysis of individual turbines. The overlaid individual results support the turbine performance integral (TPI) method introduced in Malik and Bak (2024b) and demonstrate the efficacy of the power-curve-based sensor selected. The synchronisation evident across the turbine population suggests that this approach may be suitable.

Figure 10 Synchronised seasonal performance trends for 16 wind turbines over time. Each line represents a turbine performance integral (TPI) (in kW m s⁻¹). Higher TPI values indicate better performance. The graph illustrates the high degree of synchronisation in seasonal patterns across the turbine fleet, with clear annual cycles visible.

While Fig. 10 appears dense, its primary purpose is to illustrate the high degree of synchronisation across the entire turbine set rather than to track individual turbine performance. Readers should focus on the overall pattern and synchronicity, which are consistent with the expectations of the selected sensor pair and the TPI method.

A notable observation is the tight synchronisation in performance variation signals, particularly during winter peaks and summer troughs, a pattern further delineated in the violin plots (Bechtold, 2016; Bechtold et al., 2021) presented in Fig. 11. This synchronisation, appears to be more pronounced than the coherence found in the previous work (Malik and Bak, 2024b), could indicate a more representative signal pair, despite the power curve incorporating the uncertainty in wind speed. Alternately, this may be attributed to an improvement in the quality of the underlying data, with fewer gaps caused by factors such as de-ratings or outage-type events. Such improvement in data integrity potentially stems from the weekly data buffering underlying the system, which may contribute to a more robust outcome (described in Malik and Bak, 2024b). However, it is crucial to note that buffering would still introduce “elasticity” in the signal's representation in cases with missing data, as data bins still require filling.

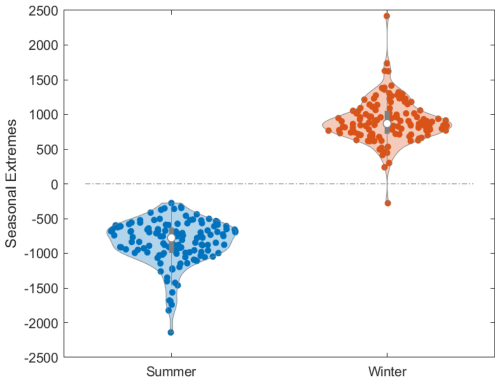
Figure 11 Violin plot comparing seasonal performance extremes for 16 turbines. Summer (left) and winter (right) variations in the turbine performance integral (TPI) are shown. Higher TPI values indicate better performance. The plot illustrates the distribution, median, and range of seasonal performance variations across the turbine fleet.

The results reveal not only the expected seasonal variations but also additional intriguing patterns that warrant further exploration. Specifically, the winter peaks display a characteristic pattern of an initial lower peak towards the end of the year, followed by a minor trough and then a pronounced peak. Similarly, the summer troughs exhibit a brief peak before descending further. These patterns appear consistent across most turbines in a given season but not across all seasons.

Since the signal is not normalised for air density variations, unlike the approach in the previous study, the observed variations encompass atmospheric conditions including temperature, wind direction, and turbulence. These distinct patterns raise questions about the specific meteorological conditions influencing these variations. Future research could focus on identifying correlations between performance patterns and weather data to gain a deeper understanding of the underlying cumulative factors driving these trends. This distinct seasonal trend in turbine behaviour may also reflect a unique signature of the specific site that could vary for identical turbines at different locations, conceptualising the turbine as an instrument measuring local atmospheric characteristics.

Moreover, the characteristic patterns within the seasonal trends warrant further investigation, potentially through an interdisciplinary collaboration with meteorologists. Such collaborations could help identify specific atmospheric phenomena driving these performance variations. Alternatively, these additional “bumps” or minor peaks in data may be mathematical artefacts intrinsic to MATLAB's implementation of STL via the “trenddecomp” function, which was employed in this work (The MathWorks, Inc., 2023). Additionally, understanding these patterns could aid in the calibration of sensor data.

The improved clarity and definition of the seasonal decomposition signal compared to previous work offers the potential to derive valuable performance understanding. For example, analysing deviations of a single turbine's performance from its historical pattern or from the trends of neighbouring turbines could signal underlying performance issues and pinpoint the need for targeted interventions or maintenance. This suggests the applicability of seasonal performance analysis as a proactive maintenance tool within wind farms.

3.2.3 Long-term trend

Figure 12 illustrates the temporal progression of 16 turbines' long-term performance. This visualisation facilitates our understanding of the overarching trends and deviations in turbine performance over the extended period, providing insights into the effects of variables such as operations and maintenance, environmental influences, and blade erosion on turbine efficiency.

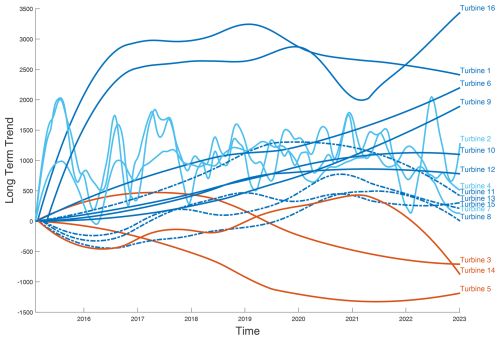
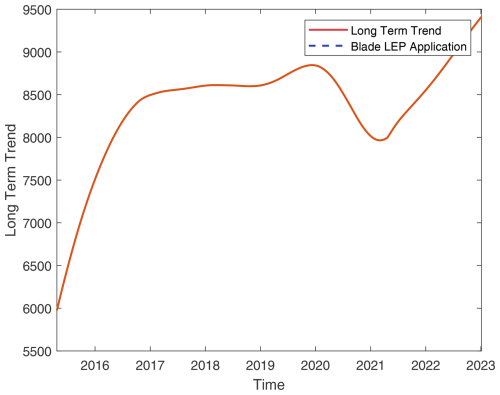
Figure 12 Grouped long-term trends in turbine performance: analysis of shared trajectories among 16 turbines, showing performance increases with value.

The zeroing of the trend data accentuates relative changes over time, enabling an examination of the performance deviations from a normalised baseline and highlighting those that diverge from the fleet’s general performance trajectory.

Turbines 4, 5, 6, 7, 8, 11, and 13 were initially commissioned without LEP, leading to accelerated wear compared to blades with LEP. The subsequent installation of LEP on these turbines at later dates potentially also influences their performance trajectories. Specifics of these LEP installations, including dates, are provided in Sect. 3.2.4.

The longitudinal analysis depicted in Fig. 12 shows a diverse array of performance trajectories across the analysed turbine fleet. Specifically, group A turbines (1, 6, 9, and 16) exhibit an upward trend, potentially indicative of improved performance stemming from successful maintenance interventions or systematic upgrades implemented over the observed period. Conversely, group B turbines (3, 5, and 14) show a downward trend suggesting progressive performance decline, possibly due to accumulated wear that maintenance efforts have not fully mitigated. Group C, including turbines 8, 11, 13, and 15, shows a somewhat stable trend.

The variable performance of turbines 2, 4, and 7 in Group D, characterised by intervals of sharp increases and decreases, aligns with patterns reported in earlier work (Malik and Bak, 2024b). Such fluctuations could result from a combination of operational dynamics and external environmental factors. Integrating this analysis with meteorological data could help clarify the underlying causes. Moreover, methodological limitations, such as the application of the STL decomposition, might also contribute to these variations. Adjusting the smoothing or other parameters to minimise “leakage” of seasonal effects into the long-term trend could improve trend fidelity, possibly causing seasonal effects to be visible in the long-term trend and preventing the misattribution of seasonal effects to climatic variability. A thorough investigation incorporating the turbines' maintenance history and regional climate conditions is warranted to clarify their impact on the observed performance dynamics.

Generally, the turbines are noted to improve or maintain performance over the period analysed, with a few exceptions that merit further investigation. While a detailed comparison with Malik and Bak (2024b) is beyond the scope of this analysis, the identification of similar patterns highlights the utility of longitudinal performance assessment. This approach aims to facilitate data-driven decision-making for maintenance and contributes to understanding the factors influencing wind turbine performance over time.

3.2.4 Influence of erosion, blade operations, and maintenance events

Informed by the synchronised seasonal trends that emphasise the importance of turbine-specific sensor selection, this section explores the impact of LEP applications and repairs on the long-term performance of a targeted subset of turbines. Figure 13 and subsequent Figs. A1 to A16, shown in Appendix A, illustrate these effects.

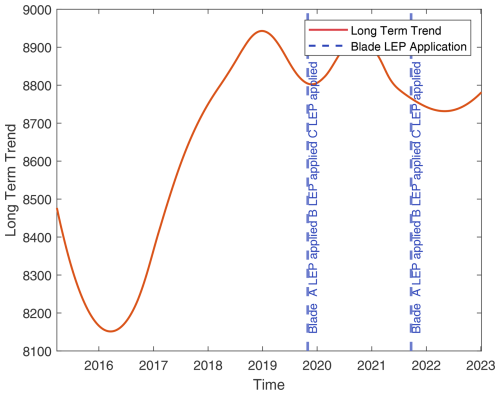
Figure 13 Overlay of blade maintenance activities on long-term turbine performance integral (TPI) trends. Performance increases with higher TPI values. Vertical dashed lines indicate blade leading-edge protection (LEP) application. The solid line represents the long-term TPI trend.

While blade-related interventions and erosion have the capacity to alter turbine performance, a multitude of other unaccounted-for factors also contribute to deviations. These include weather events, O&M events, component replacements, control system updates, measurement uncertainties, and more. A comprehensive effort to document every influencing factor and its impact is undertaken in Malik and Bak (2024b). However, it is not replicated here due to the extensive data aggregation required and the potential for inconclusive results stemming from insufficient event data in that work.

This study's further focus is identifying turbine-specific critical sensors, as evidenced by the synchronised seasonal trends. Despite the thorough analysis, erosion detection does not yield definitive conclusions, necessitating the exploration of alternative methods. In the subsequent sections, potential sensors suitable for detecting erosion will be evaluated.

3.3 Refined multibody simulations for detailed sensor evaluation

Motivated by the limited sensor availability in operational studies based on SCADA data, this investigation revisits the multibody simulation environment to examine the response of various sensors to blade roughness.

Figures 14 and 15 exemplify the changes in electrical power, attributable to two distinct degrees of blade roughness as a function of wind speed and for various turbulence intensities. The impact of erosion becomes markedly perceptible at wind speeds exceeding 9 m s⁻¹, with the P40 roughness having a more pronounced effect on the power curve. Moreover, the influence of erosion is more pronounced at lower turbulence intensities, as evidenced by the most significant change in power at 0 % TI compared to 12 % TI. An annual mean TI of 6 % is considered representative of the offshore site under investigation. This aligns with the anticipated impacts of erosion on aerodynamic efficiency and, consequently, turbine sensor readings.

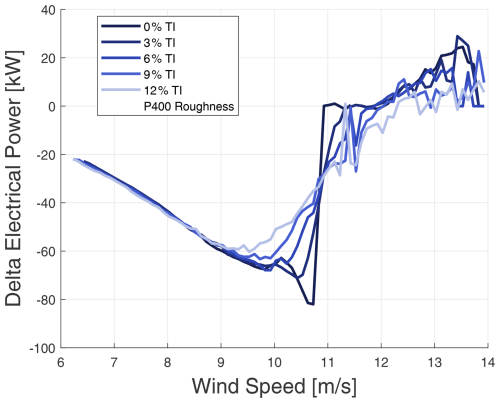
Figure 14 Delta electrical power due to P400 leading-edge roughness, compared to a clean blade, for various turbulence intensities (TI).

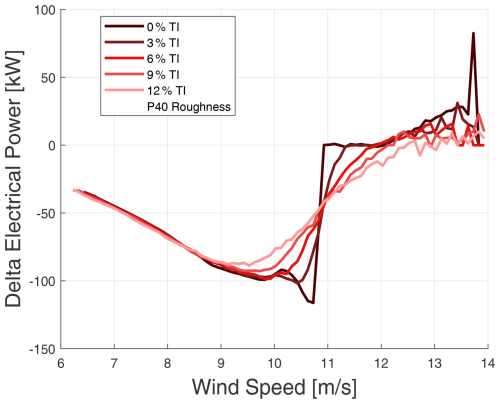
Figure 15 Delta electrical power due to P40 leading-edge roughness, compared to a clean blade, for various turbulence intensities (TI).

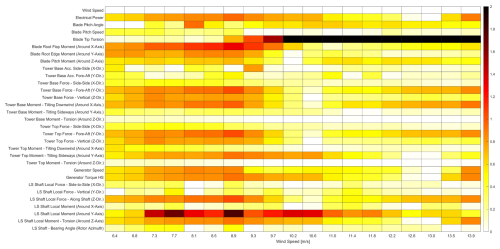
To quantify the sensitivity of various sensors to blade erosion, Cohen's d was selected as the metric of choice to provide a standardised and interpretable measure of the effect size of blade erosion (P40 roughness). This metric allows a comparison of the responsiveness of different sensors across varying wind speeds and turbulence intensities, providing insights into which sensors are most suitable for detecting blade erosion. In Fig. 16, the heat map provides a visual representation of Cohen's d values, demonstrating the differential sensitivity to erosion across varying wind speed bins for a limited suite of sensors at a turbulence intensity of 6 %. The results for 0 % and 12 % are provided in Appendix B, Figs. B1 and B2, respectively.

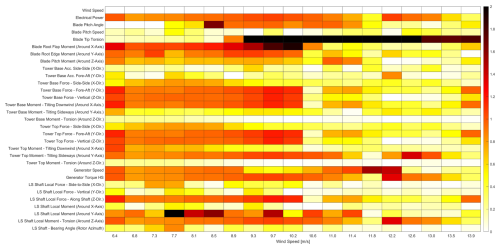
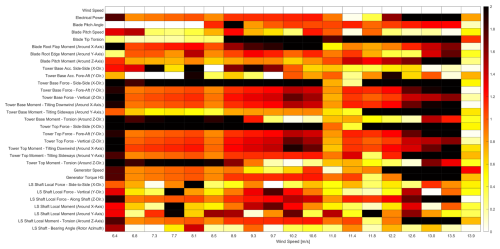
Figure 16 Heat map of Cohen's d values, showing sensor sensitivity to blade erosion (P40 roughness versus clean) across wind speeds at 6 % TI. Warmer colours indicate higher sensitivity. Absolute Cohen's d values range from 0 to 2.

Figure 16 presents a heat map of Cohen's d values for multiple sensors across different wind speeds at a TI of 6 %. This visualisation is useful for identifying the most sensitive sensors and the wind speed ranges where erosion effects are most pronounced. To interpret the heat map, observe the x axis, which represents different wind speed bins, and the y axis, which lists the various sensors being evaluated. Each cell in the heat map corresponds to the Cohen's d value for a given sensor at a particular wind speed. Warmer colours indicate higher magnitudes of change, suggesting greater sensitivity of that sensor to blade erosion, while cooler colours indicate lower magnitudes of change. This visual representation allows for quick identification of the most responsive sensors across different operational conditions.

To focus on the magnitude rather than the direction of changes in sensor readings due to blade erosion, the absolute values of Cohen’s d are taken, extending the range from 0 to 2. This adjustment simplifies the interpretation of results, as it emphasises the extent of the change rather than its direction. Moreover, the values within this range are not displayed in the figure; the figure serves solely as a guide to identify which sensors and wind speed regions warrant further analysis.

It is important to interpret the absolute values of Cohen's d in the context of the specific sensor. As an example, the response of electrical power (6 % TI and P40) relates directly to Fig. 15, herein presented in terms of Cohen's d.

Higher absolute values of Cohen's d suggest a greater sensor sensitivity, with darker colours representing a greater change in value. A value of 0 indicates no difference between the clean and rough conditions. The heat map colour scale was limited to this range to improve the visualisation of patterns across sensors, highlighting relative differences and making patterns easier to discern. While this obscures the absolute difference in sensor response, a logarithmic scale could compress the range of Cohen's d values, although it would make interpreting the magnitude of the effects less intuitive.

Sensors registering the highest Cohen's d values across multiple bins warrant particular attention in relation to the research question. The Cohen's d values for torsion at the blade tip were exceptionally higher in magnitude compared to other sensors. Values reaching approximately −13 (6 % TI) suggest either a substantial sensitivity of blade tip torsion to blade erosion conditions or potential overestimation of this sensitivity by the model. Further analysis of the blade tip torsion data is needed to determine the primary cause. The underlying torsion data may have extreme values or outliers (for both rough and clean conditions) that might be skewing the results. It should be considered whether the simulation model might be overemphasising the blade tip torsion response under certain conditions. Additionally, if the standard deviation of the blade tip torsional load is particularly small within certain conditions, even moderate differences in means can produce a large Cohen's d.

The heat map analysis reveals sensors with notable sensitivity to erosion, specifically blade tip torsion, blade root flap moment, shaft moment, and tower moments. These sensors demonstrate particular sensitivity under lower turbulence intensities (compare Figs. B1 and B2). However, care should be taken in the practical application of sensors such as the tower bottom moment, which may not be as reliable in a real-world environment as it is in simulations. This sensor's distance from the primary cause of the effect, blade erosion, can result in significant noise interference. For instance, fouling on the foundation, which may also vary over time similarly to erosion, can confound the readings from such sensors, making it challenging to attribute changes directly to blade erosion.

Although the heat map analysis reveals several key findings, it is important to acknowledge that these results are based on multibody simulations, which may have limitations in representing non-uniform inflow conditions (Boorsma et al., 2024). Additionally, the aerofoil aerodynamic model may have reduced accuracy at high Reynolds numbers, as limited validation exists for eroded aerofoil modelling under these conditions. These limitations may affect the accuracy of the sensor sensitivity analysis.

These findings provide an understanding of the capabilities of various sensors for erosion detection and performance monitoring. They emphasise the potential utility of sensors that may show promise for integration into existing SCADA or condition monitoring systems (CMSs). This integration may enable the detection of both blade erosion and performance alterations due to other potential changes stemming from blade-aerodynamic-profile-alteration-related causes.

Furthermore, these findings suggest potential benefits for wind farm owners and operators to discuss sensor inclusion with turbine manufacturers during contract negotiations. Certain sensors, such as those embedded in the drivetrain or blade lay-up, are typically installed during manufacturing and are difficult to retrofit later. Access to data from these sensors at appropriate sampling rates through standard SCADA systems could strengthen fleet monitoring capabilities. Owners and operators may want to consider requesting such access to improve their ability to monitor turbine performance over time.

4 Conclusion

This investigation explores advancements in assessing wind turbine performance using blade erosion as a proxy for detrimental performance changes. The work describes the process of utilising a turbine OEM-provided multibody model for effective sensor selection on the same operational offshore wind turbine. The turbine's wind speed anemometer, previously considered of limited utility, appears to be a crucial sensor for performance monitoring. However, the inherent uncertainties in wind speed measurements must be accounted for when interpreting performance trends, as they could significantly influence the reliability of data-driven insights.

The study applies the turbine performance integral (TPI) to a multi-megawatt turbine of a different manufacturer than in previous work (Malik and Bak, 2024b), testing the TPI's effectiveness across diverse operational contexts. This suggests the necessity of a controller-informed, turbine-specific approach to sensor selection and highlights the potential benefits of collaboration between turbine manufacturers and operators. Such partnerships would facilitate the application of proprietary-control philosophies to deploy the most appropriate sensors.

This research attempted to address the gap between simulation and operational reality by empirically examining the efficacy of an identified sensor pair in an operational turbine. Multibody simulations were used to establish the correct sensors, which were then applied to analyse seasonal performance variations. The analysis shows TPI synchronisation across 16 turbines in the same wind farm over a 9-year period, revealing overarching seasonal trends and sub-seasonal variations warranting further exploration.

However, attributing long-term performance changes to blade erosion or LEP interventions remains challenging. The multitude of operational events throughout a turbine's lifetime often obscure direct correlations between performance deviations and specific interventions. This difficulty aligns with findings from Malik and Bak (2024b), which demonstrated the challenges inherent to drawing correlations between various events in a turbine's lifetime and its performance.

To address these challenges, the investigation returned to the simulation environment. By employing Cohen’s d as a normalised metric, additional useful sensor signals were identified for the turbine investigated. Blade tip torsion, blade root flap moment, shaft moment, and tower moments exhibited heightened sensitivity to blade erosion, particularly under lower-turbulence-intensity conditions.

While the findings gained from the simulation results could not be directly compared with operational data due to lack of access or due to the potential non-existence of certain sensors, this area offers avenues for future iterative validation with results compared against empirical results to further refine the methodology. Such refinement must also consider how uncertainties in measurements impact the derived trends, particularly when the wind speed signal is employed by TPI. This may involve adjusting the simulation parameters, refining the sensor selection criteria, or incorporating additional data processing techniques. The iterative approach aims to ensure that the final set of identified sensors is both theoretically sound and practically relevant. The goal is to converge on a set of sensors that exhibit strong correlations with performance trends in operational data, potentially improving erosion monitoring. It is important to note the limitations of this approach, particularly regarding potential inaccuracies of multibody simulations in non-uniform inflow conditions. The aim is to identify reliable and practical indicators of blade-erosion-related performance changes that could be implemented in real-world turbine monitoring systems.

This study indicates the pressing need for widely available turbine-specific simulation models that accurately reflect operation under real-world conditions. Such models could be useful for fine-tuning sensor selection and deepening the understanding of turbine performance. This analysis of simulated sensor effectiveness at detecting performance reductions due to blade erosion has several potential implications for wind turbine operation and maintenance:

• Tailored sensor selection. Operators could potentially improve performance monitoring accuracy by focusing on specific sensors with high sensitivity to blade erosion, as determined through turbine-specific models.

• Sensor sensitivity. This research suggests that certain sensors are particularly sensitive to surface roughness caused by erosion. Their high Cohen's d values indicate their potential for early detection of performance degradation. The heightened sensitivity at lower turbulence intensities suggests the value of filtering datasets for calmer wind conditions to improve the likelihood of detection.

• Potential for early detection, optimised maintenance, and enhanced efficiency. Integrating sensitive sensors into existing SCADA or CMSs could enable proactive maintenance scheduling, potentially minimising energy losses and preventing severe damage. The work identifies potential sensors that may provide reliable indicators of erosion-related performance changes, supporting data-driven decision-making for improved operational efficiency and asset longevity.

Increased collaboration between academics, turbine OEMs, and operators is essential to the promotion of data-driven strategies to improve performance monitoring accuracy. This collaboration will facilitate the practical application of research findings and provide direction for future studies aimed at advancing the sustainability and efficiency of wind energy production.

Appendix A: Influence of erosion, operations, and maintenance events on all 16 turbines

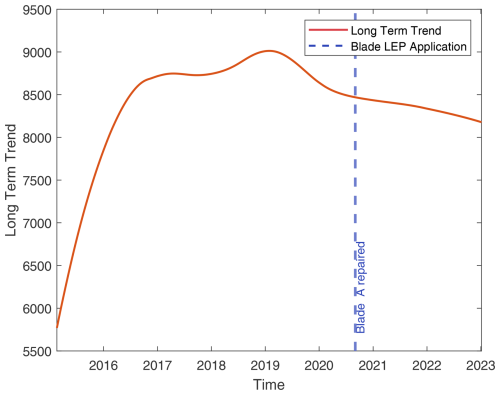
Figure A1 Turbine 1: overlay of blade maintenance activities on long-term turbine performance integral (TPI) trends. Performance increases with higher TPI values. The vertical dashed line indicates blade-leading-edge-protection (LEP) application. The solid line represents the long-term TPI trend.

Figure A2 Turbine 2: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

Figure A3 Turbine 3: overlay of blade maintenance activities on long-term TPI trends. (details as in Fig. A1).

Figure A4 Turbine 4: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

Figure A5 Turbine 5: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

Figure A6 Turbine 6: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

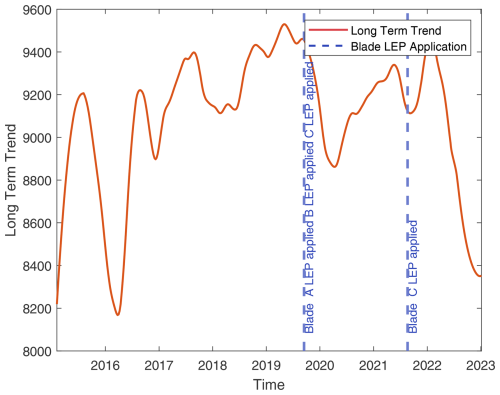
Figure A7 Turbine 7: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

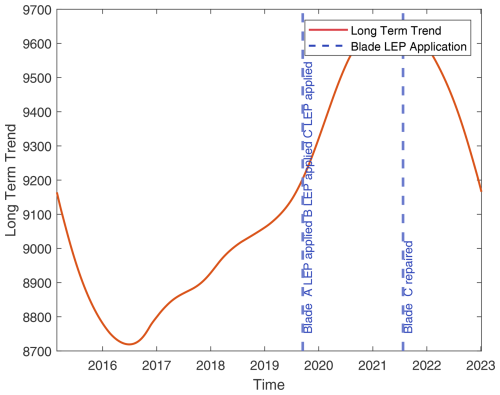
Figure A8 Turbine 8: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

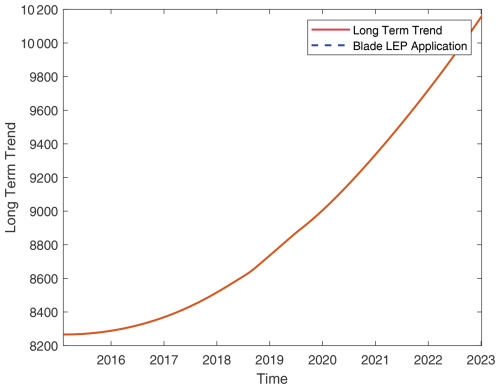
Figure A9 Turbine 9: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

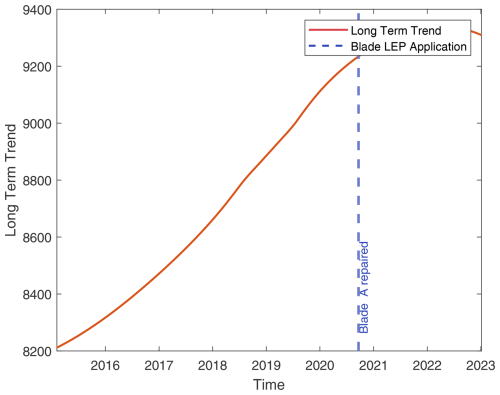
Figure A10 Turbine 10: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

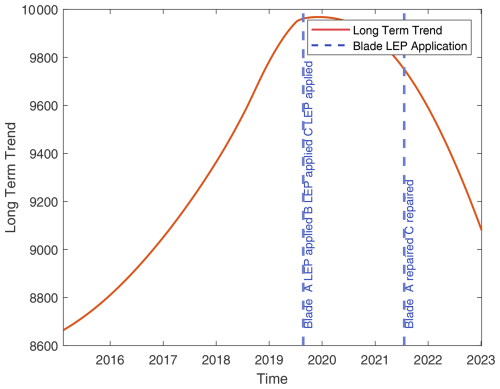
Figure A11 Turbine 11: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

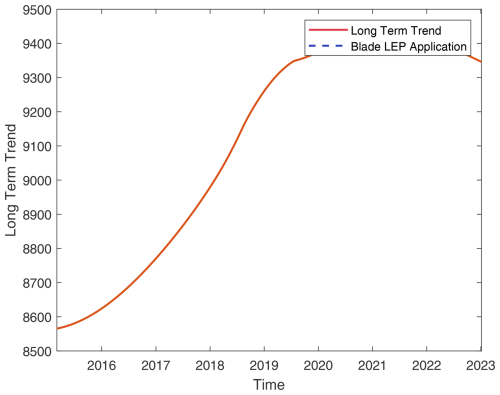
Figure A12 Turbine 12: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

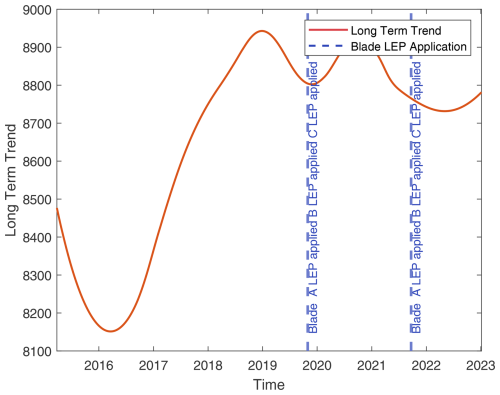
Figure A13 Turbine 13: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

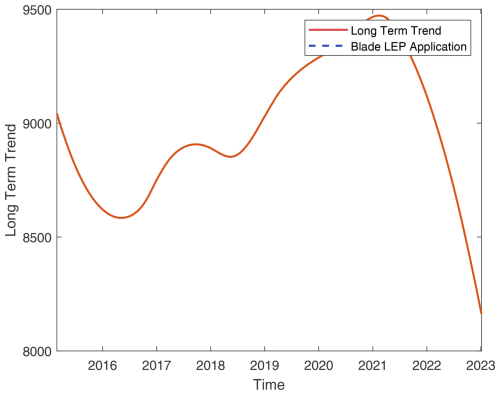
Figure A14 Turbine 14: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

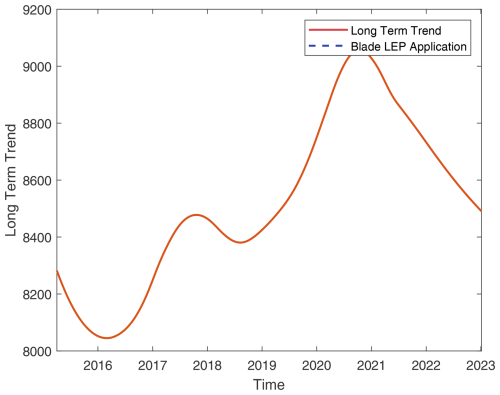
Figure A15 Turbine 15: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

Figure A16 Turbine 16: overlay of blade maintenance activities on long-term TPI trends (details as in Fig. A1).

Appendix B: Cohen's d as a function of wind speed for rough (P40) and clean conditions, for multiple sensors at various turbulence intensities

Figure B1 Cohen's d as a function of wind speed for rough (P40) versus clean conditions, for multiple sensors at 0 % TI.

Figure B2 Cohen's d as a function of wind speed for rough (P40) versus clean conditions, for multiple sensors at 12 % TI.