Ducted wind turbine optimization and sensitivity to rotor position

The design of a ducted wind turbine modeled using an actuator disc was studied using Reynolds-averaged Navier–Stokes (RANS) computational fluid dynamics (CFD) simulations. The design variables included the rotor thrust coefficient, the angle of attack of the duct cross section, the radial gap between the rotor and the duct, and the axial location of the rotor in the duct. Two different power coefficients, the rotor power coefficient (based on the rotor swept area) and the total power coefficient (based on the exit area of the duct), were used as optimization objectives. The optimal value of thrust coefficients for all designs was nearly constant, having a value between 0.9 and 1. The rotor power coefficient was sensitive to rotor gap but was insensitive to the rotor's axial location for positions ranging from upstream of the throat to nearly half the distance down the duct. Compared to the design that maximized rotor power coefficient, the design for maximal total power coefficient was characterized by a smaller angle of attack, a smaller rotor gap, and a downstream placement of the rotor. The insensitivity of power output to the rotor position implies that a rotor placed further downstream in the duct could produce the same power with a considerably smaller duct exit area and thus a greater total power coefficient. The design for that maximized total power coefficient exceeded Betz's limit with a total power coefficient of 0.67.

1 Introduction

A properly designed duct placed around a wind turbine can increase power output by increasing the mass flow rate through the rotor. Ducted wind turbines (DWTs) are also called diffuser-augmented wind turbines (DAWT) or shrouded wind turbines. Lilley and Rainbird (1956) performed a one-dimensional momentum analysis of DWTs and concluded that higher expansion ratios of the duct and more subatmospheric pressures at the exit plane of the duct result in higher power outputs. They also suggested wind tunnel tests with screens of different porosities to model the pressure drop across the rotor. Such experimental tests were performed by Igra (1976, 1977, 1981), Foreman et al. (1978), Gilbert et al. (1978), and Gilbert and Foreman (1979). The negative effect of flow separation on the power output of DWTs was observed, and various methods of preventing separation were investigated. Also, experimental tests with real turbines were performed, and the power augmentation of DWTs was demonstrated (Gilbert and Foreman, 1979, 1983; Igra, 1981). As the duct can be considered an annular wing (de Vries, 1979) with higher lift, meaning more suction and circulation, high-lift airfoils were used from early experimental studies.

Using lifting line theory for the rotor and modeling the duct as a superposition of vortex and source rings, Koras and Georgalas (1988) and Georgalas et al. (1991) studied the power output of DWTs with airfoil cross sections and large rotor gaps (the clearance between the tip of the rotor and the duct) as a function of several design variables including the angle of attack of the duct cross section, the chord length of the duct, the maximum camber of the duct cross section, and the relative position of the rotor with respect to the maximum camber point of the duct cross section. They found a linear increase of power with duct chord length and angle of attack of the duct cross section. They also concluded that the effect of rotor position on the power output was weak. Politis and Koras (1995) extended the previous work to DWTs with any rotor gap.

Axisymmetric computational fluid dynamics (CFD) models were used (Phillips et al., 1999, 2002 and Phillips, 2003) to improve the design of the first full-scale DWT built (the Vortec 7). Hansen et al. (2000) performed a CFD study of DWTs and used the k−ω shear stress transport (SST) turbulence model for the axisymmetric model as it is more sensitive to adverse pressure gradients (Menter, 1994) and can be more accurate in predicting flow separation. Another similar CFD study was performed by Abe and Ohya (2004), where effects of rotor loading and the incidence angle of the duct on power output of a flanged DWT were examined and compared with experimental data. Ohya et al. (2012) and Kardous et al. (2013) did further CFD simulations of the flanged DWT with the rotor modeled as an actuator disc and found good agreement with wind tunnel data.

Van Bussel (1999, 2007) analyzed DWTs using 1-D momentum theory and concluded that optimal coefficient of thrust in a DWT is similar to an open rotor equal to 8∕9. He also concluded that experimental power coefficients based on the exit area of the duct (the total power coefficient) above 0.5 have not been achieved yet and that very significant back pressure reductions are needed to achieve values of total power coefficients significantly above Betz's limit. Jamieson (2009) also used a similar momentum analysis and derived the same value of 8∕9 for optimal loading on the rotor and noted that it should be independent of duct design. Werle and Presz (2008) in another study based on 1-D momentum analysis found that the maximum attainable power from a DWT is determined by shroud force coefficient, $C_{\mathrm{s}}=F_{\mathrm{s}}/T$, where F_s is the axial force on the duct (shroud) and T is the thrust of the rotor.

Hjort and Larsen (2014) used an axisymmetric CFD model with an actuator disc modeling the wind turbine for a multi-element DWT. They characterized the performance of the DWT using power coefficients based on the exit area of the duct with values well above Betz's limit. Aranake and Duraisamy (2017) also utilized an axisymmetric Reynolds-averaged Navier–Stokes (RANS) solver with an actuator disc model for the turbine to optimize the airfoils used for the duct cross section and blades and verified the result with 3-D simulations. Venters et al. (2017) investigated the optimal design of a DWT using the same approach (i.e., using a RANS solver and actuator disc model). The design variables investigated were the rotor loading, the angle of attack of the duct cross section, the rotor gap, and the axial position of the rotor. They used a response surface fitted to a number of design point calculations, and then the surface was searched using the NLPQL (Nonlinear Programming by Quadratic Lagrangian) algorithm (Schittkowski, 1986). They concluded that rotor loading is the main factor defining the performance of the DWT with the coefficient of thrust almost constant (close to 1) for different duct sizes. The power output of DWT was sensitive to the angle of attack of the duct cross section. However, the results for effect of the rotor gap and axial position of rotor were not conclusive. This paper improves on the work of Venters et al. (2017) with a more accurate CFD model, a direct optimization technique, and a wider range of design variables. One of the goals of this study is to continue the investigation of Venters et al. (2017) into how the objective of the optimization changes the optimal design. Specifically, Venters et al. (2017) examined two objective functions, the rotor power coefficient and the total power coefficient. Their results indicated that the optimal design changes significantly depending on the objective function, but the results for optimizing the total power coefficient did not converge to an optimal solution. The goal of this work is to identify an optimal configuration for this objective function.

The paper is organized as follows. The details of the CFD model along with an evaluation of two different pattern search optimization methods are given in Sect. 2. Optimization results with the objective of maximizing the rotor power coefficient are given in Sect. 3, and the variation of the rotor power coefficient and flow field with different design variables is presented. In Sect. 4, optimization results are presented for the objective of maximizing the total power coefficient. These results are compared with the goal of understanding how the optimal axial position of the rotor depends on the optimization objective.

2 Method

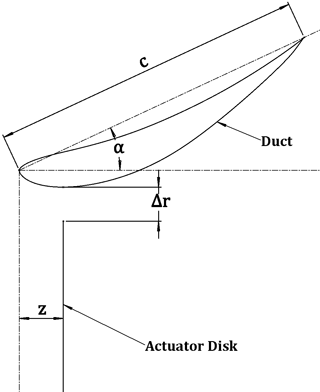
A two-dimensional axisymmetric numerical model was developed in ANSYS Fluent 17.1 to simulate the flow field of a DWT. The wind turbine rotor was modeled as an actuator disc with a pressure drop, Δp, given by

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }p={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }{V}_z^{\mathrm{2}}{C}_{\mathrm{T},\mathrm{rotor}},\end{array}$$

where ρ is the air density and C_T, rotor is the thrust coefficient based on the axial velocity, V_z, at the rotor. The thrust force, T, is given by

$$\begin{array}{}\text{(2)}& T=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{D/\mathrm{2}}{\int }}\mathrm{\Delta }pr\mathrm{d}r,\end{array}$$

where D is the rotor diameter. The extracted power, P, is given by

$$\begin{array}{}\text{(3)}& P=\mathrm{2}\mathit{\pi }\underset{\mathrm{0}}{\overset{D/\mathrm{2}}{\int }}{V}_z\mathrm{\Delta }pr\mathrm{d}r.\end{array}$$

Clearly, with an actuator disc model, rotor blade efficiency losses are not considered. The design variables, shown in Fig. 1, were the thrust coefficient of the rotor $C_{\mathrm{T},\mathrm{rotor}}=\frac{T}{\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}_z^{\mathrm{2}}{A}_{\mathrm{rotor}}}$, the angle of attack of the duct cross section α, the radial gap of the rotor Δr∕D, and the axial location of the rotor z∕c. Because the thrust coefficient based on the freestream velocity, V_∞, is easier to interpret, most results are presented in terms of $C_{\mathrm{T}}=\frac{T}{\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}_{\mathrm{\infty }}^{\mathrm{2}}{A}_{\mathrm{rotor}}}$. All results are made nondimensional by the rotor diameter, the freestream velocity, and the fluid density. The conditions studied correspond to air with a free-stream velocity of 11 m s⁻¹, a rotor diameter of 2.5 m, and a duct chord length c such that $c/D=$ 27.6 %. This corresponds to Re${}_{\mathrm{D}}=\mathrm{1.88}\times {\mathrm{10}}^{\mathrm{6}}$ and Re${}_{\mathrm{c}}=\mathrm{5.20}\times {\mathrm{10}}^{\mathrm{5}}$, where Re_D and Re_c are the Reynolds numbers based on the rotor diameter and duct chord length, respectively. An Eppler E423 airfoil was chosen as the cross section of the duct. This airfoil is designed to create high lift and operate at low Reynolds numbers. The operating range of Eppler E423 is Re${}_{\mathrm{c}}>\mathrm{2}\times {\mathrm{10}}^{\mathrm{5}}$ (Selig et al., 1996). Two power coefficients, $C_{\mathrm{P}}=\frac{P}{\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}_{\mathrm{\infty }}^{\mathrm{3}}{A}_{\mathrm{rotor}}}$ and $C_{\mathrm{P},\mathrm{total}}=\frac{P}{\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}_{\mathrm{\infty }}^{\mathrm{3}}{A}_{\mathrm{total}}}$, were used as objective functions for the optimizations and to compare the performance of different DWT designs.

Figure 1 The design variables.

The domain and mesh used for the simulations are shown in Fig. 2. These were defined to ensure mesh independence for power coefficients as the design variables were varied. The domain extended 15 duct chord lengths upstream of the rotor and 25 chord lengths downstream. Numerical tests showed that this domain size gave power coefficient values that were independent of the domain size to two significant digits. As all optimizations were done with the same domain, this was deemed large enough to accurately calculate changes in the solutions with the design variables. The shape of the domain at its top made a distinct transition between inflow and outflow boundaries, which eliminated convergence issues due to reverse flow through outlet boundaries. The reverse-flow issue occurred when the inlet and outlet were smoothly connected. The mesh of Fig. 2 consisted of about 500 000 elements. The duct boundary layer mesh had a growth rate of 1.1, and the first mesh point was set at $y^{+}\approx \mathrm{1}$. The boundary layer thickness was calculated as a function of Re_c for each case, and enough inflation layers were used to span the entire boundary layer. The quality-based smoothing option in Fluent was used to improve the mesh quality.

ANSYS Fluent's k−ω SST turbulence model was used to solve the incompressible Navier–Stokes equations. The pressure-based solver was chosen with the coupled scheme used for the pressure–velocity coupling. Gradients were calculated using the Green–Gauss node-based method, and second-order discretization schemes were used for pressure, momentum, turbulent kinetic energy, and specific dissipation rate. The output power, thrust, and drag coefficient of the duct were calculated and monitored at each iteration to ensure convergence.

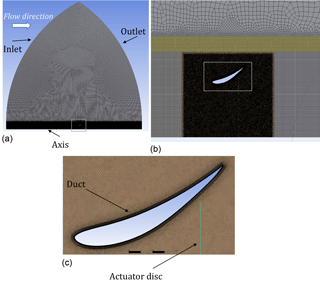
Figure 2 The domain and mesh (a); the zoomed-in view of mesh showing the structured mesh upstream and downstream of the duct (b); and the more-zoomed-in view of mesh showing the boundary layer mesh, the structured mesh of the actuator disc, and the unstructured triangular mesh between duct and the actuator disc.

Optimization techniques

For most of the optimization results, a pattern search method (Powell, 1964) was used to find the optimal design of the DWT. Optimizations were first performed with C_P as the objective function and then with C_P, total as the objective function. The optimization for both objective functions started from the same set of design variables ($C_{\mathrm{T},\mathrm{rotor}}=\mathrm{0.816}$; α=25^∘; $\mathrm{\Delta }r/D=\mathrm{0.03}$; and $z/c=\mathrm{0.14}$). In our implementation of Powell's method a quadratic interpolation of the function values is used to identify the optimal step length to move the design point in the coordinate or pattern directions. The optimization was stopped when the improvements obtained from the optimization methods were within a specified tolerance. The termination criterion was $\frac{C_{\mathrm{P},\mathrm{optimal}}-C_{\mathrm{P},\mathrm{0}}}{C_{\mathrm{P},\mathrm{0}}+C_{\mathrm{P},\mathrm{optimal}}}<\mathrm{0.005}$, where C_P,0 is the initial value of C_P at the beginning of a search cycle. The design variables were then varied to determine the sensitivity of the objective function to the design parameters in the vicinity of the optimal design point.

Powell's method is known to be slow converging for objective functions that are discontinuous. As shown in Sect. 3 and Sect. 4, it was observed that the optimal design points were on the verge of flow separation along the duct airfoil and that separation was accompanied with a large drop in power output. Therefore, the objective functions were nearly discontinuous at the optimal design point. With such an objective function, the optimizer worked inefficiently in finding the optimal step length. Also, when the optimizer moved the design point close to a discontinuity, it moved away from that point very slowly. Figure 3a shows the history of an optimization using Powell's method with $z/c=\mathrm{0.05}$ fixed and the design variables being C_T, rotor, α and Δr∕D. The optimization method was stopped at about 100 iterations without meeting its termination tolerance. At that point the search algorithm was jumping around significantly. This is shown in Fig. 3b, which shows the search history of C_T,α points. The optimal point is shown as a red triangle which occurs at C_T≈1 and α≈27^∘. The points close to each other in Powell's method that are not near the optimum point are design points close to separation where the optimizer had trouble finding the optimal step length and was stuck close to the function discontinuity. The maximum C_p obtained by the search method was 1.031.

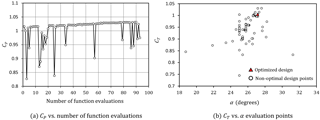
Figure 3 Optimization of C_P using Powell's method for z∕c fixed at 0.05. The red triangle denotes the optimized solution.

The same problem was subsequently approached with the Hooke and Jeeves method (Hooke and Jeeves, 1961) with the same termination criterion and starting point. The optimization history is shown in Fig. 4a. This time the optimization algorithm reached the optimal design in only 16 function evaluations and reached the termination criterion in 32 function evaluations. In addition, a better design with C_P=1.053 was found. The more efficient performance of the Hooke and Jeeves method can also be observed in Fig. 4b, which shows the (C_T, α) search points. The optimum point is again shown as a red triangle and occurred at C_T=0.97 and α=30^∘. Because the Hooke and Jeeves method does not fit an analytic function to the function values, it did not face the same difficulty when it got close to sharp variations in the objective function.

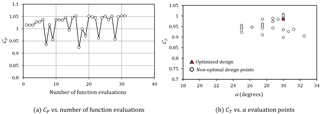
Figure 4 Optimization of C_P using Hooke and Jeeves' method for z∕c fixed at 0.05. The red triangle denotes the optimized solution.

Although the Hooke and Jeeves method was more efficient, unless stated otherwise, most of the results obtained below were found using Powell's method as this was the first method implemented. As this method did not always satisfy the optimization stopping criterion, we call the optimized designs “near-optimum” points. The search history shown in Fig. 3b is fairly typical for the cases shown below. For each search direction, function evaluations at design points in the search directions of roughly ±1 % were evaluated with no increases in the optimal value. This, however, does not preclude the possibility of a slow variation along a ridge in the optimization function, which is essentially the reason we see 5 % differences in the optimized design variables between the two different optimization methods for this example. In many of the figures below, individual design variables are varied around the optimal point to give a further sense of the sensitivity to the design variables.

3 Design for optimal C_P

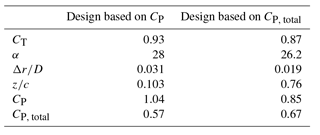
The middle column of Table 1 shows the near-optimal design found with Powell's method when optimizing for maximum C_P. The design values are close to what was observed by Venters et al. (2017). Venters et al. (2017) used a smaller chord length for the duct ($c/D=\mathrm{22.5}$ %) and a different turbulence model (k−ϵ realizable) and obtained a maximal value for C_P=1.00 at C_T=1.08 and α=37.5^∘. Our results predicted a lower value of optimal C_T and α, which could be because of the more accurate turbulence model as the k−ω SST turbulence model is known to be more accurate in prediction of flows with significant adverse pressure gradient and flow separation (Menter, 1994).

Table 1 Comparison of designs based on C_P and C_P, total

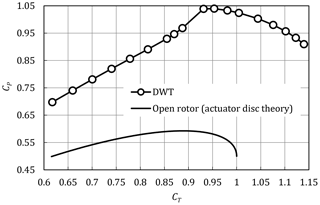
The results for the variation of C_P with C_T are shown in Fig. 5. The highest C_P in this plot is at C_T≈0.93. When using the Hooke and Jeeves optimization, optimal C_T values very close to 1 were observed, which is closer to that observed by Venters. One-dimensional momentum analysis done by van Bussel (1999) and Jamieson (2009) predicted that the optimal C_T for a ducted turbine would be independent of duct design and have a value of 8∕9, which is the same as that of an open rotor. The plot of Fig. 5 also shows the curve for an open rotor as predicted by actuator disc theory. Similar to an open rotor, increasing the loading on the rotor beyond the near-optimal design point of the DWT reduced the mass flow rate through the rotor and thus its output power. Also similar to an open rotor, at loadings less than the near-optimal design point, the flow rate through the rotor was larger, but the pressure drop was too low to obtain optimal power. In the ducted case, however, the reduction in C_T had an additional effect, which was to cause flow separation in the duct. As shown next, there is a strong coupling between the coefficient of thrust, the angle of attack of the duct, and separation. Increasing the angle of attack or decreasing the coefficient of thrust can lead to separation.

Figure 5 Variation of C_P with C_T (α=28^∘; $\mathrm{\Delta }r/D=\mathrm{0.031}$; and $z/c=\mathrm{0.103}$).

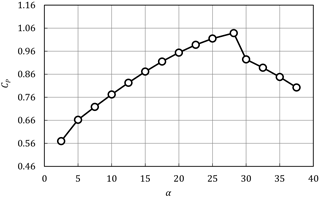
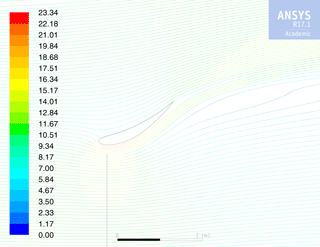
The effect of changing α is shown in Fig. 6. When α was increased beyond the near-optimal design point, a large flow separation resulted, which was accompanied by a sharp decrease in the output power. The flow field of the near-optimal design is shown in Fig. 7. The effect of increasing α on the flow field is shown in Fig. 8. Comparing the two flow fields, it is apparent that the small increase in angle of attack leads to a large separated region at the trailing edge of the airfoil. The separated region effectively reduces the exit area area of the duct, resulting in the capture of a smaller upstream flow area and a smaller power extraction. Similarly, reducing α from the near-optimal design also resulted in a decrease of C_P because of the decreased exit area.

Figure 6 Variation of C_P with α ($C_{\mathrm{T},\mathrm{rotor}}=\mathrm{0.763}$; $\mathrm{\Delta }r/D=\mathrm{0.031}$; and $z/c=\mathrm{0.103}$).

Figure 7 Streamlines at α=28.2^∘ (the streamlines are colored based on velocity magnitude in m s⁻¹).

Figure 8 Streamlines at α=30^∘ (the streamlines are colored based on velocity magnitude in m s⁻¹).

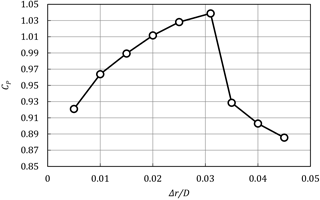
Likewise, as shown in Fig. 9, if rotor gap, Δr∕D, was increased beyond the near-optimal design point (while keeping other design variables constant), a large power drop was observed due to flow separation and the streamlines appeared similar to Fig. 8. Decreasing Δr∕D also reduced the power output of the rotor. Reduction of the rotor gap results in a decrease in the exit area of the duct, which could be the reason for the reduction in power.

Figure 9 Variation of C_P with Δr∕D ($C_{\mathrm{T},\mathrm{rotor}}=\mathrm{0.763}$; α=28^∘; and $z/c=\mathrm{0.103}$).

The dependence of C_P on the axial position of the rotor, z∕c, can be seen from Fig. 10. As z∕c was varied from the near-optimal design, the power output did not change significantly. To better understand the effect of axial location on the power output of the rotor, the design was optimized using the Hooke and Jeeves pattern search method at a number of fixed z∕c values from 0.05 to 0.35. The results shown in Fig. 10 confirm that C_P within the range of z∕c values shown is not very sensitive to the axial position of the rotor. The higher values of C_P shown are due to better performance of the Hooke and Jeeves search algorithm as discussed in Sect. 2.1. This result shows that one can place the rotor anywhere from upstream of the throat to halfway down the duct and obtain similar performance.

Figure 10 Variation of C_P with z∕c.

4 Design for optimal C_P, total

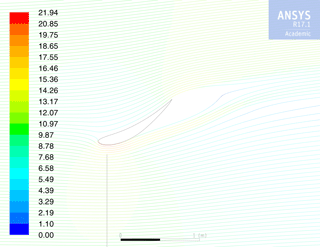
The last column of Table 1 shows the near-optimal design parameters when C_P, total was the objective function, and Fig. 11 shows the geometry and flow field of the near-optimal design. Compared to the design for optimal C_P, when a DWT was designed for optimal C_P, total, the values of α and Δr∕D were decreased, whereas z∕c was increased. All of these changes have a similar effect: to decrease the exit area of the duct, which is in the denominator of the objective function.

Figure 11 Flow field of a near-optimal design based on C_P, total.

The value of C_T of the near-optimal design (0.87) was close to the optimal C_T when C_P was optimized using Powell's method (0.93). It is also close to the optimal value for an open rotor which van Bussel (1999) and Jamieson (2009) predicted. However, there is some ambiguity in the preciseness of this value because both Venters and the Hooke and Jeeves optimization showed values near 1.00 when optimizing C_P.

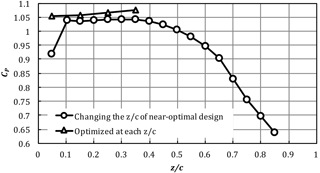
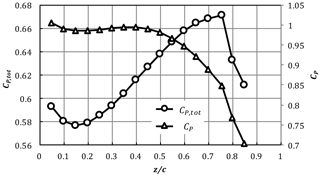
The variation of C_P, total with z∕c is presented in Fig. 12. All other design variables were fixed at the near-optimal design point for C_P, total as given in Table 1 as z∕c was varied. Since C_P, total depends on both power output and the exit area of the duct, the values of C_P at each design point are also shown so that variations due to changes in exit area or power can be better understood. Similar to Fig. 10 the power of the rotor, C_p, is not very sensitive to z∕c when $z/c<\mathrm{0.5}$. The exit area decreases as z∕c is increased, which makes C_P, total increase as the rotor is moved towards the exit of the duct. When z∕c is increased past 0.5, the power extracted decreases, but C_P, total continues to increase because of the decreasing exit area. Just past the optimal value of z∕c the flow separates, leading to a sharp decrease in both C_P and C_P, total.

Figure 12 Variation of C_P, total with z∕c ($C_{\mathrm{T},\mathrm{rotor}}=\mathrm{0.927}$; α=26.2^∘; and $\mathrm{\Delta }r/D=\mathrm{0.019}$).

The best value obtained here for $C_{\mathrm{P},\mathrm{total}}=\mathrm{0.67}$ was above Betz's limit and was also higher than the previous result by Venters et al. (2017) of 0.621. Thus, it is possible to extract more power per unit device area using a ducted turbine than when using an open rotor. This is in agreement with theoretical predictions by van Bussel (2007) at high back pressure reductions. To obtain this value of C_P, total, the rotor must be at the rear of the duct.

5 Conclusions

The optimal design of a ducted wind turbine characterized by the thrust coefficient of the rotor C_T, rotor, the angle of attack of the duct cross section α, the rotor gap Δr∕D, and the axial location of the rotor z∕c was investigated. The optimal design was significantly different when different power coefficients C_P (based on rotor area) and C_P, total (based on the exit area of the duct) were used as design objectives. Compared to the design for optimal C_P, the design for optimal C_P, total resulted in a duct with smaller α and Δr∕D and a rotor placed at the rear of the duct rather than towards the front. This type of design has been experimentally investigated in Kanya and Visser (2018).

The design for optimal C_P, total attained $C_{\mathrm{P},\mathrm{total}}=\mathrm{0.67}$, which was above Betz's limit. This optimal design was on the brink of flow separation; increases in α, decreases in C_T, or increases in Δr∕D all resulted in flow separation and a sharp decrease in power output. The Hooke and Jeeves optimization method was found to be more efficient in finding the optimal designs than Powell's method, which was attributed to this sharp variation in C_P around the design point.

Although optimal design data obtained from Powell's method should represent characteristics of a good design based on C_P or C_P, total, due to convergence issues they should be considered approximate. Also at higher Reynolds numbers (i.e., with larger DWTs) the flow field and separation characteristics of the DWT may change, which in turn can change the characteristics of the optimal design. Additionally, including effect like swirl and center body in the CFD model should give more realistic results and can change the optimal design.