The second curvature correction for the straight segment approximation of periodic vortex wakes

The periodic, helical vortex wakes of wind turbines, propellers, and helicopters are often approximated using straight vortex segments which cannot reproduce the binormal velocity associated with the local curvature. This leads to the need for the first curvature correction, which is well known and understood. It is less well known that under some circumstances, the binormal velocity determined from straight segments needs a second correction when the periodicity returns the vortex to the proximity of the point at which the velocity is required. This paper analyzes the second correction by modelling the helical far wake of a wind turbine as an infinite row of equispaced vortex rings of constant radius and circulation. The ring spacing is proportional to the helix pitch. The second correction is required at small vortex pitch, which is typical of the operating conditions of large modern turbines. Then the velocity induced by the periodic wake can greatly exceed the local curvature contribution. The second correction is quadratic in the inverse of the number of segments per ring and linear in the inverse spacing. An approximate expression is developed for the second correction and shown to reduce the errors by an order of magnitude.

1 Introduction

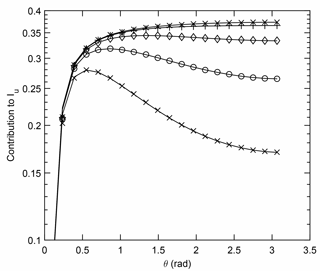
It is common for computational models of the wakes of helicopters, propellers, and wind turbines to use straight vortex segments whose position is iterated until they follow the local flow and the vortex is force free. Solving the Biot–Savart integral gives the induced velocity used in the iteration. Figure 1 shows a representation of a vortex trailing from a two-blade rotor with the straight segment approximation. The labels and symbols on the figure will be defined below. O'Brien et al. (2017) reviewed a range of computational models for wind turbines and Sarmast et al. (2016) describe a recent application of a free-wake vortex model using straight vortex segments.

Figure 1 Schematic of two turns of constant radius helical vortices with p=0.1 modelling the far wake of a wind turbine. N_b=2 and the straight segment approximation is shown for N_s=10. The flow is down the page. The “control point” is where the induced velocity is required. The contribution from the “aligned segments” on either side of the control point require the largest second curvature correction.

A well-known difficulty of the straight segment approximation is that it does not reproduce the binormal velocity due to the curvature of the vortex line (e.g. Bhagwat and Leishman, 2014, Govindarajan and Leishman, 2016, and Kim et al., 2016). This leads to the need for the first curvature correction. To assess the errors of the straight segment approximation and develop a correction, Bhagwat and Leishman (2014) used a vortex ring whose binormal (axial) velocity, U, is given by the well-known Kelvin equation

$$\begin{array}{}\text{(1)}& U={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}\text{log}\left({\displaystyle \frac{\mathrm{8}}{a}}\right)-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}},\end{array}$$

where Γ is the circulation of one vortex, and a is the radius of the vortex core (e.g. Saffman, 1992). Figure 2 shows the vortex ring approximation to the helical wake in Fig. 1. Note that by Eq. (1) U increases as a decreases. In this equation, and throughout this paper, all lengths are normalized by the vortex radius (not the core radius a) and all velocities by the wind speed. To reproduce Eq. (1), the numerical evaluation of the Biot–Savart integral for the ring is “cut off” by ignoring the contribution from distances smaller than a from the point at which the velocity is required, the “control point” shown in Figs. 1 and 2. It is emphasized that the cut-off is a heuristic; Kelvin's equation (Eq. 1) is usually derived from impulse considerations or other methods that do not use the Biot–Savart law. Saffman (1992) documented many factors that alter the vortex velocity from its Biot–Savart value: these include flow along the vortex axis, differing distributions of swirl, etc. Nevertheless, the Biot–Savart prescription is useful and computationally convenient.

Curvature in the wakes of rotors is often associated with vortex periodicity, the “return” of a vortex to the proximity of the control point, which can cause a significant contribution to the binormal velocity. Wood and Li (2002) and Wood (2004) used helical line vortices to analyze straight segment errors for this second effect of curvature, but their work has apparently not been considered in subsequent vortex modelling. Govindarajan and Leishman (2016) claimed that the second curvature correction is unnecessary and difficult to implement. The purpose of this paper is to document the importance of the second correction for wind turbine wakes under some operating conditions and to develop an effective and simple correction.

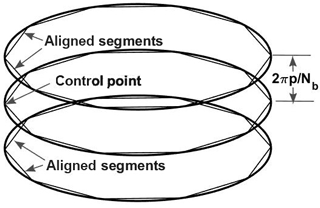
Figure 2 Vortex ring representation of the helical wake in Fig. 1 and the corresponding vortex segment approximation.

The paper is organized as follows. The next section introduces the vortex ring model of the wake. In the following section, the induced velocity for the periodic component of the wake over a range of vortex spacings is found in terms of its Biot–Savart integral. Section 4 describes the calculation of the induced velocity for the straight segment approximation, determines the second curvature correction, and tests its accuracy. The final section contains the conclusions.

2 The vortex ring model for the wake

For a point with the same radius as a single vortex ring and distance z from it, the Biot–Savart equation for U in the direction of the wind – the binormal direction – is

$$\begin{array}{}\text{(2)}& U={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+z^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\mathrm{d}\mathit{\theta },\end{array}$$

where θ is the vortex angle in cylindrical polar co-ordinates. If z=0, the integral clearly has a logarithmic singularity as θ→0. The velocity, U_1c, requiring the first curvature correction is

$$\begin{array}{}\text{(3)}& U_{\mathrm{1}\mathrm{c}}=U(z=\mathrm{0}),\end{array}$$

arising from the only ring containing the control point. The integral in Eq. (2) and similar equations will be termed the “influence coefficient” I, which has the same relative error characteristics as U.

The test case used here to investigate the second correction models the far wake of a wind turbine as an infinite row of equispaced vortex rings of constant spacing, s, radius, and Γ, extending to infinity on either side of the control point at z=0. A row of rings is easier to analyze than the helical vortices used by Wood and Li (2002) and Wood (2004) but displays the same need at small separation for the second correction. In addition, the discrete nature of the vortex rings helps to localize the correction that is developed in Sect. 4.

The ring vortex wake is consistent with the “Joukowsky” model of the wake, used by Sarmast et al. (2016); either the bound vorticity of the blades is constant along their span or all the shed vorticity has rolled up into tip and hub vortices before reaching the far wake. This is clearly a simplification of wind turbine wakes in general, but the linearity of the Biot–Savart law allows more complex wakes to be considered as an assembly of elements such as rings. The velocity associated with the second correction, U_2c, is induced by the vortices that do not contain the control point:

$$\begin{array}{}\text{(4)}& U_{\mathrm{2}\mathrm{c}}={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}{I}_{\mathrm{2}\mathrm{c}}={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}\mathrm{2}\sum _{j=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+(js{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\mathrm{d}\mathit{\theta }.\end{array}$$

Equation (4) is not singular as θ→0, which is, possibly, the reason why the need for the second correction has not been appreciated. s can be identified with the pitch p of a helical vortex wake and the number of blades, N_b, according to $s=\mathrm{2}\mathit{\pi }p/N_{\mathrm{b}}$. The relationship between p and s can be seen by comparing Figs. 1 and 2.

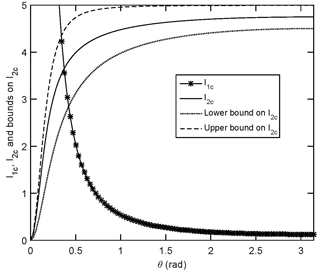
Figure 3 The integrands for the two influence coefficients for a control point on the vortex ring and θ₀=0. The stars show the integrand for I_1c from Eq. (2) with z=0. The solid line shows I_2c. The dashed and dotted lines are the bounds on I_2c, Eq. (5) with s=0.2. The sums were evaluated using Eq. (4) for 50 000 rings.

Testing corrections for the straight segment approximation requires an accurate evaluation of the series in Eq. (4) and then an integration in θ. This order is preferred because the integration in θ of the summand results in incomplete elliptic integrals, which are likely to be very difficult to sum. The innocuous looking series in Eq. (4), however, does not appear to have a closed form sum. The standard technique for summing infinite series of algebraic functions is via Laplace transforms (e.g. Wheelon, 1954). This would be successful if the exponent in the integrand was 1 instead of 3∕2, but for Eq. (4), the method gave a principal value integral that could not be solved in closed form. By the Cauchy integral test for series

$$\begin{array}{ll}{\displaystyle \frac{\mathrm{1}}{s}}& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}}}}\le I_{\mathrm{2}\mathrm{c}}\left(\mathit{\theta }\right)\le {\displaystyle \frac{\mathrm{1}}{s}}-{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}}}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{2}(\mathrm{1}-\cos \mathit{\theta })}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}},\end{array}$$

where

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{I}_{\mathrm{2}\mathrm{c}}=\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}{I}_{\mathrm{2}\mathrm{c}}\left(\mathit{\theta }\right)\mathrm{d}\mathit{\theta }\text{ and }\\ \text{(6)}& {\displaystyle }& {\displaystyle }{I}_{\mathrm{2}\mathrm{c}}\left(\mathit{\theta }\right)=\sum _{j=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+(js{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}.\end{array}$$

It is easy to show that the average velocity in the direction of the wind at any radius r<1 within the Joukowsky wake is $\mathrm{1}-\mathrm{\Gamma }/s$ (e.g. Wood, 2011), and it is reasonable to assume that the total velocity of the free-wake vortex rings is close to $\mathrm{1}-\mathrm{\Gamma }/\left(\mathrm{2}s\right)$ or the induced velocity, $U\approx \mathrm{\Gamma }/\left(\mathrm{2}s\right)$. Further, the bounds in Eq. (5), which both contain 1∕s, cause U to approach the average of the wake and external velocities, provided the curvature singularity does not contribute significantly to U. There is, unfortunately, only limited experimental information on a and U for wind turbine wakes to guide the assessment of the relative importance of the first and second velocity fields and their corrections. Figure 3 shows the terms in Eq. (5) for s=0.2. This typical value was obtained using the following steps. For modern turbines, N_b=3, and λ≈7 for most of the operating range. For optimal (Betz-Joukowsky) performance, $U=\mathrm{1}/\mathrm{3}$, $p\approx \mathrm{2}/\left(\mathrm{3}\mathit{\lambda }\right)$, where λ is the tip speed ratio, and $N_{\mathrm{b}}\mathrm{\Gamma }\mathit{\lambda }/\mathit{\pi }=\mathrm{8}/\mathrm{9}$ (Wood, 2011). Thus Γ=0.133 and s≈0.2. The sum in Eq. (4) is always zero when θ=0, but, as s decreases, the bounds in Eq. (5) (and hence the sum) tend to 2π∕s over an increasing range of θ. Integrating over [0,2π] then leads to $U\approx U_{\mathrm{2}\mathrm{c}}\approx \mathrm{\Gamma }/\left(\mathrm{2}s\right)$, showing the potential importance of U_2c. The integrand of I_1c for a small θ is also shown. Its integral and U_1c depend on the cut-off, a; to match $U=\mathrm{2}/\mathrm{3}$ for the conditions in Fig. 3, Eq. (1) requires $a\sim {\mathrm{10}}^{-\mathrm{23}}$, which does not seem a reasonable value. Thus it is likely that U≈U_2c at the small p and s typical of the operating conditions of modern wind turbines.

The very limited experimental information on the velocity of the vortices in wind turbine wakes are in general agreement with this argument. Xiao et al. (2011) measured the wake of a two-bladed turbine in a wind tunnel at λ=4.91 using particle image velocimetry. They determined the vortex velocity in the near wake as 10.8 m s⁻¹ when the wind speed was 12 m s⁻¹. Thus $U=(\mathrm{12}-\mathrm{10.8})/\mathrm{12}=\mathrm{0.1}$, which is lower than the value of 1∕3 that follows from assuming optimal power output. Assuming U=U_2c and using the general equation $p=(\mathrm{1}-U)/\mathit{\lambda }$ gives s=0.576 or 360 mm for the rotor of radius 625 mm, which agrees very well with the value read from their Fig. 10. This again implies that U_2c≫U_1c. Since most rotor wakes are helices of some form, it is important to note that the equivalent inverse pitch term dominates U for a helical vortex of sufficiently small p (Kuibin and Okulov, 1998). There is a further reason to expect $U\approx U_{\mathrm{2}\mathrm{c}}\gg U_{\mathrm{1}\mathrm{c}}$ for many turbine wakes: U_1c, but not U_2c, is associated with the impulse necessary to form a vortex ring. If that impulse and U_1c are significant it is unlikely that the wake can be force free.

3 Evaluating the influence coefficient for an infinite array of vortex rings

A closed form sum for U_2c in Eq. (4) could not be obtained so the influence coefficients for a range of s values were determined as follows. The Hermite–Hadamard inequality for monotonically decreasing functions that tend to zero at large argument can be used simply to give a tighter bound on I_2c(θ). It is

$$\begin{array}{}\text{(7)}& I_{\mathrm{2}\mathrm{c}}\left(\mathit{\theta }\right)={\displaystyle \frac{\mathrm{1}}{s}}-{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}}}}+{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}+\mathit{\delta }\left(\mathit{\theta }\right),\end{array}$$

where the difference, δ(θ), is always positive but must be determined numerically. The integral of the other terms on the right side of Eq. (7) can be found exactly:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}\left({\displaystyle \frac{\mathrm{1}}{s}}-{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}}}}+{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\right)\mathrm{d}\mathit{\theta }\\ \text{(8)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{2}\mathit{\pi }}{s}}-{\displaystyle \frac{\mathrm{2}sE(-\mathrm{4}/s^{\mathrm{2}})}{s^{\mathrm{2}}+\mathrm{4}}}-{\displaystyle \frac{\mathrm{2}K(-\mathrm{4}/s^{\mathrm{2}})}{s}},\end{array}$$

where E(.) and K(.) are the complete elliptic integrals in standard notation. The difference, δ, the integral of δ(θ) over [0,2π], was evaluated using 2000 increments of θ and number of rings, N_r=50 000. This value was chosen using the result obtained from Mathematica, that

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}\mathrm{2}\sum _{j=N_{\mathrm{r}}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+(js{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\mathrm{d}\mathit{\theta }\\ \text{(9)}& {\displaystyle }& {\displaystyle }\to R\left(N_{\mathrm{r}}\right)={\displaystyle \frac{\mathrm{4}\mathit{\pi }\left(\mathit{\zeta }\right(\mathrm{3})-H_{N_{\mathrm{r}}}^{\left(\mathrm{3}\right)})}{s^{\mathrm{3}}}}\end{array}$$

for large N_r, where ζ(.) is the zeta function, and H is the harmonic number in standard notation. In later use of this result, R(j) will be called the “remainder”. Using 2π∕s as an estimate for the integral in Eq. (4), and using Mathematica to evaluate H₃(N_r), gave the relative error in truncating the sum at N_r=50 000 as $\mathrm{2}/s^{\mathrm{2}}\times {\mathrm{10}}^{-\mathrm{10}}=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{8}}$ for the smallest value of s considered here, s=0.1. To the number of decimal places used in Table 1, truncation does not alter the integral of the terms in Eq. (7) over [0,2π]. For every calculation up to Sect. 5, N_r=50 000. The θ−integral of the sum in Eq. (7) was found using the MATLAB quadrature routine “integral” with an absolute tolerance of 10⁻⁸. All integrands are symmetric about θ=π and so were obtained over [0,π]. Table 1 also shows the approximate λ for a Betz–Joukowsky optimal rotor. δ is small: combining Eqs. (6) and (7) leads to

$$\begin{array}{}\text{(10)}& \mathrm{0}\le \mathit{\delta }\le {\displaystyle \frac{\mathrm{2}K(-\mathrm{4}/s^{\mathrm{2}})}{s}}-{\displaystyle \frac{\mathrm{2}sE(-\mathrm{4}/s^{\mathrm{2}})}{s^{\mathrm{2}}+\mathrm{4}}},\end{array}$$

which is satisfied by all δ values in Table 1. δ is less than 4 % of I_c for the worst case of s=0.8; Eq. (8) is an increasingly good approximation to the sum and the influence coefficient approaches 2π∕s as s decreases and λ increases. The values of I_2c in Table 1 will be compared to the values from the straight segment approximation.

Table 1 Values of the influence coefficient for varying s values with θ₀=0.

4 Straight segment approximation of vortex rings and its accuracy

Each of the rings not containing the control point was approximated by an even number, N_s, of straight segments. The ith segment of each ring started at $\mathit{\theta }=\mathrm{2}\mathit{\pi }i/N_{\mathrm{s}}+{\mathit{\theta }}_{\mathrm{0}}$ when measured from the control point and finished at $\mathrm{2}\mathit{\pi }(i+\mathrm{1})/N_{\mathrm{s}}+{\mathit{\theta }}_{\mathrm{0}}$. θ₀ is the angular displacement between the control point and the start of the first (i=0) segment. A straightforward application of Eq. (10.115) of Katz and Plotkin (2001) gives I_2c(i,j), the contribution of the ith segment on the two jth vortex rings to U_2c, as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{U}_{\mathrm{2}\mathrm{c}}(i,j)={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}\sum _{j=\mathrm{1}}^{N_{\mathrm{r}}}\sum _{i=\mathrm{1}}^{N_{\mathrm{s}}}{I}_{\mathrm{2}\mathrm{c}}(i,j),\text{ where }\\ \text{(11)}& {\displaystyle }& {\displaystyle }{I}_{\mathrm{2}\mathrm{c}}(i,j)={\displaystyle \frac{A_i{B}_{i,j}}{C_{i,j}}},\end{array}$$

and

$$\begin{array}{ll}\text{(12)}& {\displaystyle }{A}_i& {\displaystyle }=\mathrm{8}\sin ({\displaystyle \frac{\mathit{\pi }i}{N_{\mathrm{s}}}}+{\displaystyle \frac{{\mathit{\theta }}_{\mathrm{0}}}{\mathrm{2}}})\sin ({\displaystyle \frac{\mathit{\pi }(i+\mathrm{1})}{N_{\mathrm{s}}}}+{\displaystyle \frac{{\mathit{\theta }}_{\mathrm{0}}}{\mathrm{2}}}),{\displaystyle }{B}_{i,j}& {\displaystyle }=\sin {\displaystyle \frac{\mathit{\pi }}{N_{\mathrm{s}}}}({\displaystyle \frac{\mathrm{1}}{b_{i+\mathrm{1},j}}}+{\displaystyle \frac{\mathrm{1}}{b_{i,j}}})\\ \text{(13)}& {\displaystyle }& {\displaystyle }+\sin ({\displaystyle \frac{(\mathrm{2}i+\mathrm{1})\mathit{\pi }}{N_{\mathrm{s}}}}+{\mathit{\theta }}_{\mathrm{0}})({\displaystyle \frac{\mathrm{1}}{b_{i+\mathrm{1},j}}}-{\displaystyle \frac{\mathrm{1}}{b_{i,j}}}),{\displaystyle }{C}_{i,j}& {\displaystyle }=\cos {\displaystyle \frac{\mathrm{2}\mathit{\pi }}{N_{\mathrm{s}}}}+b_{i,j}^{\mathrm{2}}+b_{i+\mathrm{1},j}^{\mathrm{2}}\\ \text{(14)}& {\displaystyle }& {\displaystyle }+\cos ({\displaystyle \frac{\mathrm{2}\mathit{\pi }(\mathrm{2}i+\mathrm{1})}{N_{\mathrm{s}}}}+\mathrm{2}{\mathit{\theta }}_{\mathrm{0}})-\mathrm{2},\end{array}$$

and

$$\begin{array}{}\text{(15)}& b_{i,j}=\sqrt{\mathrm{2}-\mathrm{2}\cos ({\displaystyle \frac{\mathrm{2}\mathit{\pi }i}{N_{\mathrm{s}}}}+{\mathit{\theta }}_{\mathrm{0}})+(js{)}^{\mathrm{2}}}.\end{array}$$

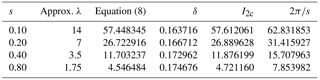
For the first calculations, the junction of the first and N_sth segment was aligned with the control point so θ₀=0. The influence coefficients calculated from Eqs. (11)–(14) are compared to the results from Table 1 in Fig. 4 in terms of the relative error using the integral over [0,π] as the denominator since the integrand must be symmetric about θ=π. The error is defined as the exact integral minus the straight segment approximation so the latter is always an underestimate. Two separate ranges of θ are considered: for $\mathrm{0}\le \left|\mathit{\theta }\right|\le \mathit{\pi }/\mathrm{2}$ the error is 1 to 2 orders of magnitude higher than for $\mathit{\pi }/\mathrm{2}\le \left|\mathit{\theta }\right|\le \mathit{\pi }$ and the errors in the first range increase with decreasing s whereas in the second range they decrease. Figure 5 shows the reason. For this test case, no aligned segment contributes to U_2c as the Biot–Savart velocity must lie in the plane containing the segment and the control point. Otherwise, both errors scale as $\mathrm{1}/N_{\mathrm{s}}^{\mathrm{2}}$, as was found in the helix simulations of Wood (2004). As s decreases, however, the aligned segment error increases proportionally to 1∕s, but the error for the remaining range of θ decreases at constant N_s.

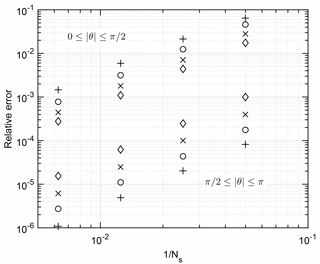
Figure 4 Relative error of the straight segment approximation for the conditions in Table 1 (θ₀=0). +: s=0.1; ^∘: s=0.2; ×: s=0.4; ◇: s=0.8. The top group of symbols show the errors for the first half of the rings that contain the aligned segments, $\mathrm{0}\le \left|\mathit{\theta }\right|\le \mathit{\pi }/\mathrm{2}$, and the bottom group covers $\mathit{\pi }/\mathrm{2}\le \left|\mathit{\theta }\right|\le \mathit{\pi }$. $N_{\mathrm{s}}=\mathrm{20},\mathrm{40},\mathrm{80}$, and 160.

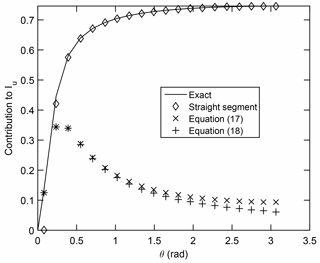
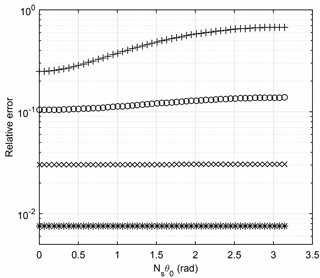
Figure 5 Angular contribution of straight segments to the influence coefficient for z=0.2, N_s=40, and θ₀=0. The value of θ is the midpoint of the segment. The solid line shows the numerical solution of the exact integral. ◇ shows the straight segment contribution, × the contribution from Eq. (17), and + the contribution from Eq. (18).

Figure 5 shows the angular contribution to the influence coefficients for s=0.2 and N_s=40. The value of θ used for plotting is the midpoint of each segment. The solid line shows the exact integral from θ_i to θ_i+1. As was found by Wood and Li (2002) and Wood (2004), the errors are localized near θ=0. A correction for the error for the aligned segments can be developed from the small-θ expansion of the series in Eq. (4):

$$\begin{array}{ll}{\displaystyle }{I}_{\mathrm{2}\mathrm{c}}\left(\mathit{\theta }\right)& {\displaystyle }=\mathrm{2}\sum _{j=\mathrm{1}}^{\mathrm{\infty }}{I}_{\mathrm{2}\mathrm{c}}(\mathit{\theta },j)=\sum _{j=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{\mathrm{2}-\mathrm{2}\cos \mathit{\theta }}{(\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+(js{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\\ \text{(16)}& {\displaystyle }& {\displaystyle }\to {\displaystyle \frac{\mathit{\zeta }\left(\mathrm{3}\right){\mathit{\theta }}^{\mathrm{2}}}{s^{\mathrm{3}}}}\text{ as }\mathit{\theta }/s\to \mathrm{0}\end{array}$$

and ζ(3)=1.2026. Equation (16) has two important implications. First, the best possible error for periodic straight segments scales as (N_ss)⁻³ but it is likely that an unrealistically high value of N_s would be required to achieve this. Second, 1∕ζ(3) or over 80 % of the correction to U_2c is due to the two rings (j=1) on either side of the control point. This is the justification for pointing out the aligned segments in Figs. 1 and 2. A general form of the correction, therefore, can be based on the returned vortex on either side of the control point. Since the distance from the control point to the vortex segments must be calculated in a free-wake simulation, it should not be difficult to determine the proximity in terms of θ∕z and apply a correction. A more general correction is Δ(θ_s), where ${\mathit{\theta }}_{\mathrm{s}}=\mathrm{2}\mathit{\pi }/N_{\mathrm{s}}$ is obtained by integrating in θ only for j=1 and then using ζ(3) to correct approximately for the remaining rings. The result is

$$\begin{array}{ll}{\displaystyle }\mathrm{\Delta }\left({\mathit{\theta }}_{\mathrm{s}}\right)& {\displaystyle }\approx \mathrm{2}\mathit{\zeta }\left(\mathrm{3}\right)[{\displaystyle \frac{F\left({\mathit{\theta }}_{\mathrm{s}}/\mathrm{2},-\mathrm{4}/s^{\mathrm{2}}\right)}{s}}-{\displaystyle \frac{sE\left({\mathit{\theta }}_{\mathrm{s}}/\mathrm{2},-\mathrm{4}/s^{\mathrm{2}}\right)}{s^{\mathrm{2}}+\mathrm{4}}}\\ \text{(17)}& {\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{2}\sin {\mathit{\theta }}_{\mathrm{s}}}{\left(s^{\mathrm{2}}+\mathrm{4}\right)\sqrt{\mathrm{2}-\mathrm{2}\cos {\mathit{\theta }}_{\mathrm{s}}+s^{\mathrm{2}}}}}],\end{array}$$

where E(.) and F(.) are the incomplete elliptic integrals. Equation (17) is shown in Fig. 3 to give a better estimate for the aligned segments. An alternative, simpler correction than Eq. (17) can be found by using $\mathrm{2}-\mathrm{2}\cos \mathit{\theta }\sim {\mathit{\theta }}^{\mathrm{2}}$ for small θ values to give

$$\begin{array}{}\text{(18)}& \mathrm{\Delta }\left({\mathit{\theta }}_{\mathrm{s}}\right)\approx \mathrm{2}\mathit{\zeta }\left(\mathrm{3}\right)\left[\log \left({\displaystyle \frac{{\mathit{\theta }}_{\mathrm{s}}+\sqrt{{\mathit{\theta }}_{\mathrm{s}}^{\mathrm{2}}+s^{\mathrm{2}}}}{s}}\right)-{\displaystyle \frac{{\mathit{\theta }}_{\mathrm{s}}}{\sqrt{{\mathit{\theta }}_{\mathrm{s}}^{\mathrm{2}}+s^{\mathrm{2}}}}}\right],\end{array}$$

which gives almost the same correction for the aligned segments; Fig. 5. These results for the application of Eqs. (17) and (18) to the aligned segments are similar at the other values of s as well, but are not shown in the interests of brevity. It is noted that the correction developed here is simple in the sense that the vortex curvature is known a priori. As pointed out by Govindarajan and Leishman (2016), however, and shown by the analysis of Kim et al. (2016), the modelling of three-dimensional wakes of varying geometry can be considerably more complex.

Figure 6 Variation in relative error with θ₀ for s=0.1. N_s=20, +; N_s=40, ^∘; N_s=80, ×; N_s=160, ⋆.

One of these complexities is that the control point may not align with the junction of segments on (in this case) adjacent rings. The effect of this can be investigated by using non-zero θ₀ in Eqs. (12)–(15). The results are shown in Fig. 6 for $\mathrm{20}\le N_{\mathrm{s}}\le \mathrm{160}$ and $\mathrm{0}\le {\mathit{\theta }}_{\mathrm{0}}\le \mathit{\pi }/N_{\mathrm{s}}$ and s=0.1. As was found for other values of s, there is remarkably little variation in the error with θ₀ except for the lowest N_s, suggesting that the correction derived above for the aligned case (θ₀=0) is also applicable to other values. This is not an immediately obvious result from Eqs. (12)–(15). For ${\mathit{\theta }}_{\mathrm{0}}=\mathit{\pi }/N_{\mathrm{s}}$ and $\mathit{\theta }=\mathrm{2}\mathit{\pi }/N_{\mathrm{s}}$:

$$\begin{array}{ll}{\displaystyle }{I}_{\mathrm{2}\mathrm{c}}(\mathit{\theta },\mathrm{1})& {\displaystyle }={\displaystyle \frac{\mathrm{8}{\sin }^{\mathrm{2}}(\mathit{\theta }/\mathrm{2})\sin \mathit{\theta }}{\left(\mathrm{3}-\mathrm{4}\cos \mathit{\theta }+\cos \mathrm{2}\mathit{\theta }+\mathrm{2}{s}^{\mathrm{2}}\right)\sqrt{\mathrm{2}-\mathrm{2}\cos \mathit{\theta }+s^{\mathrm{2}}}}}\\ \text{(19)}& {\displaystyle }& {\displaystyle }\to ({\displaystyle \frac{\mathit{\theta }}{s}}{)}^{\mathrm{3}}\text{as}\mathit{\theta }/s\to \mathrm{0},\end{array}$$

which suggests a difference from the case when θ₀=0.

Figure 7 Variation in the straight segment approximation to I_2c(θ) for θ₀=0 and N_r= 5, ×; 10, ^∘; 20, ⋄; +, 50; ×, 50 000. N_s=40, s=0.2.

5 Using a finite array of rings to determine the influence coefficient

The second curvature error was shown in the last section to be caused largely by aligned segments on the rings either side of the control point. For increasing θ, I_2c(θ) becomes dominated by rings at a larger distance from the control point. This is shown in Fig. 7, which implies that N_r either must be large to ensure an accurate determination of I_2c or a suitable remainder term be used. This allows an approximate determination of the influence coefficient for the case in which θ₀=0 according to

$$\begin{array}{}\text{(20)}& I_{\mathrm{2}\mathrm{c}}\approx \mathrm{2}\mathrm{\Delta }\left({\mathit{\theta }}_{\mathrm{s}}\right)+\sum _{j=\mathrm{1}}^{N_{\mathrm{r}}}\sum _{i=\mathrm{1}}^{N_{\mathrm{s}}}{I}_{\mathrm{2}\mathrm{c}}(i,j)+R\left(N_{\mathrm{r}}\right),\end{array}$$

where one possibility for the remainder R(N_r) is given by Eq. (9).

Table 2 Terms in Eq. (20) for s=0.2 and θ₀=0. Exact value of I_2c=26.889628. The error is the relative error.

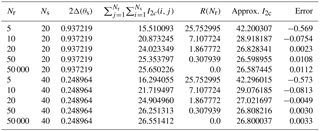
The terms in Eq. (20) are listed in Table 2 for s=0.2. A significant number of vortex rings, N_r, or equivalently a large stream-wise distance is needed to make the remainder, R(N_r), accurate. Typically, N_r≥20 for this s, and then R(N_r) is comparable to Δ(θ_s). For N_s=20, for example, after applying an accurate remainder, the second curvature correction changes the relative error from 3.4 % to less than 0.2 %, which is a reduction by 2 orders of magnitude.

6 Conclusions

The widely used straight segment approximation for approximating the curved and periodic vortex wakes of wind turbines, propellers, and helicopters can have two errors associated with the wake curvature. The first is the well-known error in reproducing the locally induced binormal velocity. This is usually accommodated by a cut-off in the Biot–Savart determination of the vortex velocity using Eqs. (2) and (3) at a distance comparable with the radius of the vortex core. The second, less well-known error is the subject of this paper. It arises from the alignment of the segments of the periodic vortex returning to the proximity of the point at which the velocity is being determined.

By modelling the far wake of a wind turbine as an infinite row of equispaced vortex rings, two important results were obtained. First, it was shown that the velocity associated with the second error dominates at the small spacings typical of modern wind turbine operation. The available experimental evidence on wake structure is consistent with this finding. Then it is shown that the second error is quadratic in the number of segments per revolution and inversely proportional to the spacing of the rings, which is proportional to the pitch of a more realistic, but more difficult, helical wake. The model to investigate the second correction is artificial in that a single, infinite row of vortex rings of constant spacing, radius, and circulation is not applicable to the near wake. Nevertheless the model demonstrated the general importance of the rings adjacent to the control point at which the velocity is being calculated. These adjacent rings contribute over 80 % of the correction that is needed because the straight segment approximation does not correctly determine the contribution to the induced velocity from the closest parts of the adjacent rings, called the aligned segments.

It was also shown that the best behaviour possible for the second error is cubic in the product of the number of segments per revolution and the vortex spacing. It is likely, however, that larger numbers of vortex segments would be needed to achieve this error than are used in practice. This result was generalized to develop a second correction that improves the computed induced velocity by nearly 1 order of magnitude.