More accurate aeroelastic wind-turbine load simulations using detailed inflow information

In this paper, inflow information is extracted from a measurement database and used for aeroelastic simulations to investigate if using more accurate inflow descriptions improves the accuracy of the simulated wind-turbine fatigue loads.

The inflow information is extracted from nearby meteorological masts (met masts) and a blade-mounted five-hole pitot tube. The met masts provide measurements of the inflow at fixed positions some distance away from the turbine, whereas the pitot tube measures the inflow while rotating with the rotor.

The met mast measures the free-inflow velocity; however the measured turbulence may evolve on its way to the turbine, pass beside the turbine or the mast may be in the wake of the turbine. The inflow measured by the pitot tube, in comparison, is very representative of the wind that acts on the turbine, as it is measured close to the blades and also includes variations within the rotor plane. Nevertheless, this inflow is affected by the presence of the turbine; therefore, an aerodynamic model is used to estimate the free-inflow velocities that would have occurred at the same time and position without the presence of the turbine.

The inflow information used for the simulations includes the mean wind speed field and trend, the turbulence intensity, the wind-speed shear profile, atmospheric stability-dependent turbulence parameters, and the azimuthal variations within the rotor plane. In addition, instantaneously measured wind speeds are used to constrain the turbulence.

It is concluded that the period-specific turbulence intensity must be used in the aeroelastic simulations to make the range of the simulated fatigue loads representative for the range of the measured fatigue loads. Furthermore, it is found that the one-to-one correspondence between the measured and simulated fatigue loads is improved considerably by using inflow characteristics extracted from the pitot tube instead of using the met-mast-based sensors as input for the simulations. Finally, the use of pitot-tube-recorded wind speeds to constrain the inflow turbulence is found to significantly decrease the variation of the simulated loads due to different turbulence realizations (seeds), whereby the need for multiple simulations is reduced.

1 Introduction

Aeroelastic simulations are extensively used in the development of modern wind turbines. These simulations are used to estimate the dynamic response of the wind-turbine structure in both the research, the design and the certification phase. They are specifically used to investigate new concepts, evaluate various designs, and eventually to prove that the code-defined lifetime fatigue loads and extreme loads are below the capability limits of the wind-turbine subcomponents.

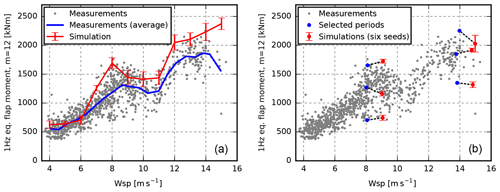
Figure 1 Two approaches for comparing the measured and simulated loads. (a) The traditional approach where the site-average turbulence characteristics and shear profile are used as input for the aeroelastic simulations. The results are compared to the measured average load levels. (b) The suggested one-to-one approach where measured inflow characteristics are extracted from selected time series. The simulation results are compared to the corresponding measurement observation. Note that the simulation error bars are offset 1 m s⁻¹ to the right to increase clarity.

To validate aeroelastic codes, simulation results are usually benchmarked against results from other aeroelastic codes, compared to measurements of scaled wind-turbine models under laboratory conditions, or compared to measurements on full-scale turbines. In this paper, we focus on the ultimate approach, where simulation results are compared to full-scale measurements.

Aeroelastic simulations are typically based on idealized simplified models of the wind-turbine structure (e.g. often modelled as beam-type structures), its aerodynamic properties (e.g. often based on the blade element momentum aerodynamic approach, Hansen, 2015) and the inflow conditions. In the present paper, the focus is on the accuracy of the inflow specification and the derived component load consequences, when validating an aeroelastic model by comparing simulations with full-scale measurements. The state-of-the-art aeroelastic model HAWC2 is used for this analysis, and the load results are compare to measurements from the DAN-AERO project (Madsen et al., 2010c).

The paper is structured as follows. Initially, determination of inflow characteristics, matching a particular full-scale event, are discussed in some detail. Next, the experimental section is described which encompasses both the experimental set-up and the measured results for selected case studies. Then a description of the analogue numerical simulations follows, and these simulations are subsequently compared with the selected full-scale recordings. Finally, conclusions are drawn.

2 Problem discussion

The inflow conditions obviously have a significant impact on the turbine load response (Elliott and Cadogan, 1990; Eggers et al., 2003; Antoniou et al., 2007; Wagner et al., 2011; St. Martin et al., 2016).

The inflow conditions are typically decomposed into an average stationary part and a turbulent fluctuating part. In many cases, the code-defined or the site-averaged shear profiles and turbulence parameters are used in the inflow modelling. This approach makes it possible to compare simulation results with the average load level resulting from the full-scale measurements (see Sect. 3.1) despite the often massive measurement scatter, which is mainly caused by variability in the inflow conditions. An example is shown in Fig. 1a.

This paper is about the effects of using more precise and dedicated inflow characteristics for aeroelastic simulations when dealing with validation of aeroelastic codes. The idea is to extract detailed information about the inflow from a selection of 10 min measurement periods with the aim of defining accurate inflow fields characteristics of each of the periods, i.e. descriptions of the mean inflow velocities, and the turbulent fluctuations. These inflow characteristics are subsequently used as input for numerical load simulations, and the simulated loads are then compared with the measured loads in a one-to-one comparison (see Fig. 1b).

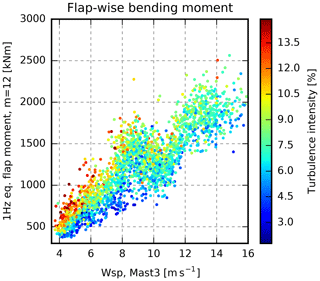
Figure 2 The blade-root flap-wise fatigue load plotted as a function of wind speed (Wsp) and coloured by turbulence intensity. The turbulence intensity affects the blade-root fatigue loads. However, much of the scatter is caused by other factors.

Table 1 Case overview showing the origin of the mean wind speed (wsp), wind speed trend, turbulence intensity (Tint), shear profile and Mann parameter (L, Γ and αϵ^2∕3) values that were used for each of the five cases. The last column shows which sensor was used as input for the constraint turbulence simulation.

As seen in Fig. 2, the measured blade-root fatigue load increases with the wind speed. However, the scatter is massive. Different levels of turbulence intensity can explain some of the variation, especially for low wind speeds, but a substantial part of the variation is caused by a combination of other factors, e.g. variability in the wind shear profile, atmospheric stability, and so on. Therefore, the hope is that it will be possible to extract dedicated accurate inflow characteristics for a given measurement period, and, based on these characteristics, to reproduce the period in an aeroelastic simulation giving close to similar loads. In this way, a one-to-one validation of a given aeroelastic code is facilitated, which in turn paves the way for improved future aeroelastic prediction capabilities. In addition, the measurement period required for load validation can potentially be reduced by using a reduced set of single time series instead of the average of a large measurement dataset. This is because the statistical significance of the simulated results based on accurate detailed inflow conditions is expected to be superior to results obtained from average site wind characteristics.

The inflow characteristics required for the description of more accurate inflow fields can be extracted from cup or sonic anemometers at a nearby meteorological mast (met mast) if the anemometers are exposed to similar inflow conditions. This means that the mast must be close to the turbine, but outside of the rotor induction zone. Furthermore, wind directions during which the anemometers are in the wake of turbines or the mast itself must be discarded, as well as situations in which the turbine is in the wake of other turbines. In addition, anemometers are required at different heights to measure the mean wind shear profile. Wind veer (i.e. turning of the mean wind direction with height) is not considered in this study.

Alternatively, the inflow parameters can be obtained from a blade-mounted flow sensor (BMFS). Mounted at the blade, a BMFS is exposed to exactly the same inflow conditions as the turbine, and this is true regardless of the wind direction. In addition, a BMFS also provides valuable information about the flow variations within the rotor area.

However, a BMFS is located inside the rotor induction zone; therefore, a method to compensate for the presence of the turbine in the flow recordings is required, i.e. a method that takes the flow velocities measured with the BMFS and calculates the free-stream inflow velocities that would have been observed at the same time and location without the presence of the wind turbine. In such studies, the method presented by Pedersen et al. (2018) can be used. This procedure uses a combination of aerodynamic models to estimate the disturbance that the turbine induces on the free-stream inflow.

3 Measurements

From the measurement database (see Sect. 3.1), 20 different 10 min periods, denoted P1–P20, are extracted. These periods are selected to be no-wake situations and represent a wide range of load levels at 8 and 14 m s⁻¹, i.e. below and above the rated wind speed. From each of the 20 periods, inflow characteristics are extracted for five different simulation cases, cases 1–5. Case 1 uses the mean wind speed only, Case 2 utilizes additional information about wind-speed trend, turbulence intensity and shear, etc. (see Sect. 4.2 and Table 1).

For each case and period, the inflow characteristics are used as input for a set of six aeroelastic simulations with different turbulence realizations (seeds).

3.1 Site, turbine, sensor and data overview

The measurement database used in this study was recorded from April to July 2009 as part of the DAN-AERO project (Madsen et al., 2010c; Troldborg et al., 2013). It contains 9600 data files with 10 min measurements from a Siemens 3.6 MW wind turbine located at the Høvsøre test site for large wind turbines in Denmark, as well as measurements from the nearby met masts (see Fig. 3). The rotor diameter is 107 m and the hub height is 89.5 m. The turbine was equipped with blade-root bending-moment sensors and a blade-mounted five-hole pitot tube.

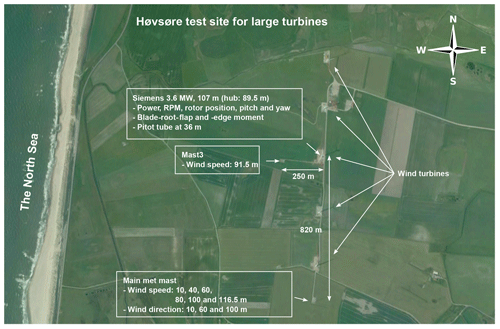
Figure 3 Overview of the Høvsøre test site for large wind turbines in Denmark. The Siemens turbine is located in the middle of a row of five megawatt turbines.

As seen in Fig. 3, the turbine was located in the middle of a row of five megawatt-scale wind turbines. Mast3, which is located around 2.5 diameters west of the turbine, provides hub-height wind-speed observations, whereas the main met mast, 820 m south of the turbine, measures the wind speed at six different heights ranging from 10 to 116.5 m.

3.2 Blade-mounted five-hole pitot tube

Five-hole pitot tubes have been used in several research experiments to measure the local inflow relative to the blades (Madsen and Markkilde Petersen, 1990; Madsen, 1991; Brand et al., 1996; Petersen and Madsen, 1997; Schepers et al., 1997; Simms et al., 1999; Hand et al., 2001a, b; Schepers et al., 2002; Madsen et al., 2003, 2010c; Medina et al., 2011, 2012).

During the current measurement period, an Aeroprobe CPSPY5 five-hole pitot tube was mounted on one of the blades at a radius of 36 m, i.e. around one-third from the tip. A five-hole pitot tube measures the relative flow speed as well as the flow angle in two perpendicular planes. The pitot tube was calibrated by Aeroprobe, and the uncertainty of the measured relative flow speed and angles was determined to be less than 0.2 % and 0.2^∘ respectively (Madsen et al., 2010b).

From the relative flow speed and two perpendicular angles, the relative 3-D flow velocity vector can be calculated (Telionis et al., 2009), and subtracting the velocity due to sensor movement yields the flow velocity in the rotor plane; more details about this process, the measurement database and measurement-related issues are available in Pedersen et al. (2017).

In this study, the velocity due to sensor movement is calculated based on the rotor rotation and the pitch motion. This means that movement due to dynamic tower and blade deflection is not included, and some discrepancy is consequently expected. In Pedersen et al. (2018), the error introduced by not taking the tower and blade deflection into account is investigated using HAWC2 simulations, and the root-mean-squared error of the instant axial wind speed is found to be around 2 %.

The flow velocity is mapped from the rotating blade section coordinate system to fixed global cartesian coordinates. During this process, additional uncertainty is introduced, as the exact orientation of the blade section is unknown due to the deflection and torsion of the structure.

Finally, the wind-turbine induction, i.e. the disturbance of the inflow field caused by the presence of the rotor, is estimated using a combination of aerodynamic models. In this study, the aerodynamic models comprise blade element momentum (BEM) based models for axial and tangential induction, a radial induction model and tip loss correction, as well as models for skew and dynamic inflow.

Subtracting the estimated induction from the measured flow velocity results in an estimate of the free-stream inflow velocity, which would have been observed at the same time and location without the presence of the turbine. In this step, uncertainty is also introduced due to the mismatch between the applied simple engineering models and the complex real world. The process and the introduced uncertainties are described in detail by Pedersen et al. (2018). Furthermore, based on numerical simulations, Pedersen et al. (2018) found that the error of the estimated axial 10 min mean wind speed obtained from a BMFS is less than 0.25 m s⁻¹ for all wind speeds, whereas the error of the standard deviation is less than 0.1 m s⁻¹. Whether the introduced uncertainties outweigh the advantage of measuring at the blade will be investigated in this study.

3.3 Calibration of load sensors

The blade-root load sensors comprise flap-wise and edge-wise bending-moment sensors (see Fig. 4) on all three blades. They are located 3.2 m from the hub centre.

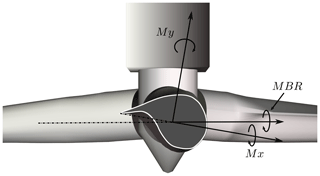
Figure 4 Orientation of the blade-root flap-wise, M_x, and edge-wise, M_y, bending-moment sensors. These sensors pitch with the blade. MBR is the no-pitch rotor-plane projection of the blade-root bending moments.

Some of the sensors are found to drift considerably with temperature. Therefore, a linear temperature correction is applied before performing the calibration.

The edge-wise bending-moment sensors are calibrated using a set of time series measured at low wind speed and with pitch angles around 0^∘. In these cases, the edge-wise loads are dominated by the gravity loading; therefore, the loads are fitted to a sinusoidal signal with a magnitude equal to the self-weight moment of the blade:

$$\begin{array}{}\text{(1)}& \underset{a,b}{\text{Minimize}}\left(\sum _{{\mathit{\theta }}_{\text{rotor}}}\left|aMy\left({\mathit{\theta }}_{\text{rotor}}\right)+b-M_{\text{sw}}\sin \left({\mathit{\theta }}_{\text{rotor}}\right)\right|\right),\end{array}$$

where a and b are calibration factors, My is the measured edge-wise bending moment, θ_rotor is the rotor position and M_sw is the moment when the blade is in the horizontal position due to the weight of the blade from the load sensor to the tip.

Similarly, the flap-wise bending-moment sensors can be calibrated using time series measured at a low wind speed and a 90^∘ pitch angle. However, the measurement database does not contain time series with a 90^∘ pitch angle and low wind speed; it was, therefore, necessary to use time series with lower pitch angles for the calibration. Hence, the pitch angle must be included in the calibration formula:

$$\begin{array}{ll}\text{(2)}& {\displaystyle }& {\displaystyle }\underset{a,b}{\text{Minimize}}{\displaystyle }& {\displaystyle }\left(\sum _{{\mathit{\theta }}_{\text{rotor}}}\left|aMx\left({\mathit{\theta }}_{\text{rotor}}\right)+b-M_{\text{sw}}\sin \left({\mathit{\theta }}_{\text{pitch}}\right)\sin \left({\mathit{\theta }}_{\text{rotor}}\right)\right|\right),\end{array}$$

where M_x is the measured flap-wise bending moment, and θ_pitch is the pitch angle.

The mean flap-wise bending moments of the three blades are not equal after this calibration. This is, however, justified as the measured pitch angles of blades 2 and 3 are offset by around −0.4 and +1^∘ respectively, compared with blade 1. These pitch offsets are included in the aeroelastic simulations (see Sect. 4).

3.4 Derived tower-load sensors

The current measurement database contains no tower-load sensors. The dynamic tower loads are, however, mainly induced by the aerodynamic blade loads; therefore, it is possible to derive tower-load estimations from the blade-root load sensors.

The tower-bottom fore–aft bending moment is dominated by the constant weight of the rotor and the dynamic thrust on the rotor. The thrust is related to the rotor-plane projection of the blade-root bending moments (i.e. mainly the flap-wise bending moments), and using a linear calibration a good approximation can be achieved for a given wind speed:

$$\begin{array}{}\text{(3)}& {\text{MTB}}_{\text{foreaft,est}}=a_{\text{tb}}\sum _{i=\mathrm{1}\mathrm{\dots }\mathrm{3}}{\text{MBR}}_i+b_{\text{tb}},\end{array}$$

where MTB_foreaft,est is the estimated tower-bottom fore–aft bending moment, MBR_i is the rotor-plane projection of the blade-root bending moment of blade i (see Fig. 4), and a_tb and b_tb are calibration constants.

Similarly, approximations of the tower-top tilt and yaw moments can be formulated as

$$\begin{array}{ll}\text{(4)}& {\displaystyle }& {\displaystyle }{\text{MTT}}_{\text{tilt,est}}={\displaystyle }& {\displaystyle }{a}_{\text{tilt}}\sum _{i=\mathrm{1}\mathrm{\dots }\mathrm{3}}{\text{MBR}}_i\cos \left({\mathit{\theta }}_{\text{rotor}}-{\displaystyle \frac{\mathrm{2}i}{\mathrm{3}}}\mathit{\pi }\right)+b_{\text{tilt}}\\ \text{(5)}& {\displaystyle }& {\displaystyle }{\text{MTT}}_{\text{yaw,est}}={\displaystyle }& {\displaystyle }{a}_{\text{yaw}}\sum _{i=\mathrm{1}\mathrm{\dots }\mathrm{3}}{\text{MBR}}_i\cos \left({\mathit{\theta }}_{\text{rotor}}-{\displaystyle \frac{\mathrm{2}i}{\mathrm{3}}}\mathit{\pi }+{\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}\right)+b_{\text{yaw}}\end{array}$$

The derived tower-load sensors have been calibrated based on HAWC2 simulations. Applied to other HAWC2 simulations with comparable wind conditions, the tower loads derived from the blade-root sensors fit quite well with the actual simulated tower loads (see 8 m s⁻¹ example in Fig. 5).

The calibration constants are, however, dependent on the mean wind speed. Hence, the fine agreement seen in Fig. 5 is only obtainable when using the correct wind-speed-specific calibration constants.

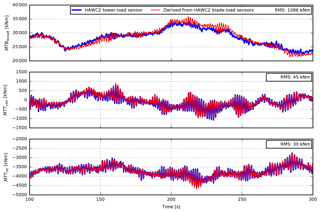
Figure 5 Comparison of the HAWC2 simulated tower loads and the estimated tower loads, which are derived from the HAWC2 simulated blade-root load sensors and calibrated for 8 m s⁻¹.

The calibration constants are consequently determined for wind speeds ranging from 4 to 15 m s⁻¹ and interpolated based on the revolution-averaged pitot-tube mean wind speed. To test the calibration, the equivalent fatigue load of the derived tower-load sensors have been calculated for five independent simulation sets. The estimated loads are then compared to the HAWC2-simulated “real” tower loads. The relative error is shown in Fig. 6.

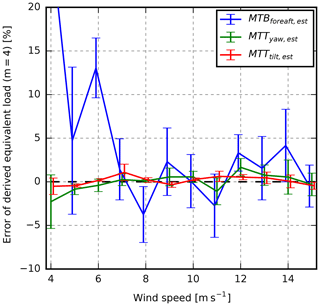
Figure 6 Relative fatigue load error of the derived tower-load sensors compared to the HAWC2 simulated tower loads. The derived tower-load sensors are obtained from the HAWC2 simulated blade-root load sensors and calibrated using wind-speed-dependent calibration constants.

At low wind speeds, the tower-bottom bending moment is dominated by structural loads, whereas the impact of the aerodynamic blade loads is limited. Hence, the derived tower-bottom sensor deviates considerably from the simulated tower-bottom signal, and the fatigue load error is relatively high (see Fig. 6). Therefore, the derived tower-bottom fore–aft loads will be discarded for wind speeds below 6 m s⁻¹. In all other cases, the mean error is less than 5 %. Note that this deviation will not affect the discrepancies between the measurements and simulations in the results section directly, as the presented tower loads in both cases will be derived from the blade-root loads even though the “real” tower loads are also simulated directly by HAWC2.

4 Simulations

To facilitate comparisons of the predicted loads with their measured counterparts, aeroelastic simulations were performed.

4.1 Simulation model

The simulations used in this study are performed using HAWC2 – a non-linear finite-element-based aeroelastic code intended for computing the wind-turbine response in the time domain (Madsen et al., 2010a, 2012; Kim et al., 2013; Larsen et al., 2015).

The turbine model used for the simulations is based on the structural and aerodynamic data of the Siemens 3.6 MW turbine, which was tested at Høvsøre in 2009 during the DAN-AERO project (see Sect. 3.1).

To match the pitch-angle offsets observed in the measurements (see Sect. 3.4), the blades are modelled with slightly different pitch angles.

Within the HAWC2 framework, the turbine is controlled by the Basic DTU controller (Hansen and Henriksen, 2013). This controller has been set up to match the behaviour of the Siemens controller, which was controlling the turbine during the measurement period, as well as possible. In some cases and regions, however, mismatch between the two controllers should be expected.

4.2 Inflow characteristics

In this section, the inflow characteristics used for the different cases are described (see an overview of the five cases in Table 1). Cases 1–3 are based on met-mast sensors, whereas cases 4 and 5 are based on the estimated free-stream pitot-tube wind speed (see Sect. 3.2). Table 2 gives an overview of the actual inflow parameters extracted from the 20 periods.

Table 2 Inflow characteristics of P1–P20 showing the wind speed (Wsp), wind speed trend (Trend), turbulence intensity (Turb. int.) and power shear exponent (Power shear exp).

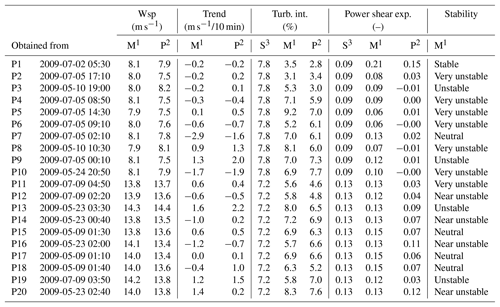
¹ Mast3 ∕ main met mast; ² Pitot tube; ³ Mast3 ∕ main met mast (site average).

4.2.1 Wind speed

In cases 1–3, the 10 min mean wind speed measured at Mast3 is used. Mast3 is located around 2.5 rotor diameters west of the turbine (see Fig. 3). Therefore, its 10 min mean wind speed is expected to match the mean wind speed at the rotor quite well as far as the selected periods are concerned.

In cases 4 and 5, the mean wind speed is extracted from the estimated free-stream pitot-tube wind speed. To avoid the problem regarding the influence of non-linear shear on the mean wind speed, only observations recorded in the 85–95 m altitude regime are included (i.e. the hub height ±5 m on both sides of the rotor).

4.2.2 Wind-speed trend

In some of the selected periods, the mean wind speed changes considerably during the period. Therefore, a linear wind-speed trend is assumed and calculated for all periods and is included in the simulations in all cases except for Case 1.

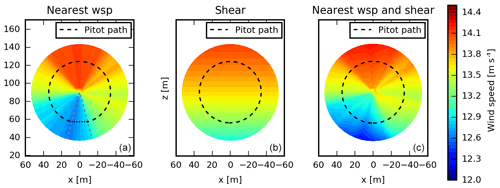
Figure 7 (a) Wind speed based on the nearest pitot-tube wind speed (interpolated values are used in a 30^∘ sector around the tower to the exclude the effects of tower shadow). (b) Wind speed based on the 1 h power shear profile. (c) Wind speed based on the nearest pitot-tube wind speed and power shear profile.

Wind-speed trends may result in increased loads, e.g. tower-bottom fatigue loads, as the trend will contribute with one (large) fatigue cycle. Furthermore, the target turbulence intensity will be too high if calculated from the standard deviation of the raw wind-speed signal. Note, however, that periods with wind-speed trends may be problematic, as it means that the turbulence conditions are not stationary, and the theory behind the applied turbulence model assumes stationary conditions.

4.2.3 Shear and mean wind-speed variation

The mean wind shear profile has a high impact on the flap loads as well as on the tower-top tilt and yaw loads. The 10 min mean wind speed is not known in all parts of the rotor, and, therefore, a shear model is necessary. In this study, the power-law type of shear profile is used, and it is fitted to 1 h of measurements. As the wind may change during 1 h, we would like to base the shear profile on the selected 10 min observations. However, the 10 min mean vertical profile can have almost any shape, and a longer time period is therefore usually required to make a proper power-profile fit.

In Case 1, the site-average wind-speed-dependent shear profile is used, whereas the mean wind speeds at different heights, measured at the main met mast 850 m away, are used to estimate the vertical shear profile for cases 2 and 3. Note, that the main met mast has sensors up to 116.5 m, and the upper part of the rotor is therefore not represented.

It is possible to use the 10 min mean shear profile measured by the pitot tube directly, but outside of its altitude range a shear profile model is required. Therefore, the power-law shear profile is fitted to 1 h of the estimated free-stream pitot-tube wind speed and is used for cases 4 and 5.

Ideally the 10 min mean wind speed is known for the whole rotor. This is obviously not the case, but from the pitot-tube measurements, the 10 min mean wind speed at the path of the pitot tube can be extracted and used to specify the mean wind speed in a grid covering the rotor (see Fig. 7a). This information is used in combination with the 1 h power shear profile (Fig. 7b) to specify a grid-based mean wind-speed field for Case 5 (see Fig. 7c).

The aerodynamic models that are used to estimate the free-stream pitot-tube wind speed do not include a model of the tower shadow. The wind-speed drop due to tower shadow should not, however, be included in the inflow input to the simulations. Therefore, the mean wind speed is linearly interpolated in a 30^∘ sector around the tower as indicated in Fig. 7a.

4.2.4 Turbulence

The turbulence used in the simulations is generated using the Mann turbulence model (Mann, 1994, 1998). This model requires three parameters as input: a length scale of the spectral velocity tensor, L, an energy dissipation factor, αϵ^2∕3, and a shear distortion parameter, Γ. Standard parameters can be used, or they can, alternatively, be fitted to the turbulence spectra calculated from a long recording period of e.g. 3-D sonic measurements.

For cases 1, 4 and 5, standard values are used for L and Γ as specified in IEC (6140), whereas fitted values are used for cases 2 and 3.

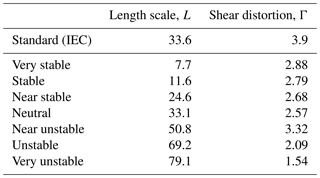
The Mann turbulence model assumes neutral atmospheric stability conditions. The parameters can, however, be fitted to spectra representing non-neutral stability classes where slightly different parameters are obtained. The stability-dependent parameters used for cases 2 and 3 (see Table 3) are extracted from Peña et al. (2010), where the turbulence at the current site was investigated.

Table 3 Standard and stability-dependent turbulence parameters.

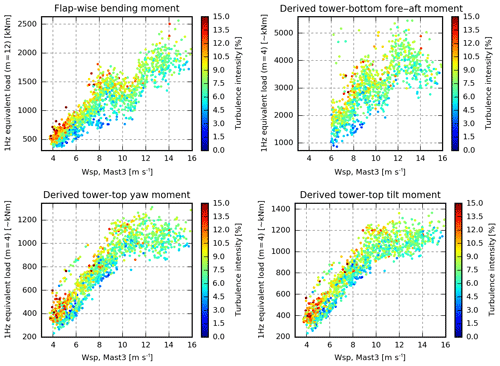
Figure 8 The 1 Hz equivalent loads coloured by the magnitude of the turbulence intensity measured at Mast3.

Standard or long-term-average values may be appropriate for L and Γ, but as we want to simulate the current situation, and not a monthly or yearly average, another approach is required for the αϵ^2∕3 parameter; this parameter is proportional to the turbulence intensity for fixed L and Γ and, in turn, related to the fatigue equivalent loads.

In Case 1, the turbulence is scaled after generation, such that the turbulence intensity in the centre of the turbulence field matches the turbulence intensity measured by Mast3 within the selected period. This approach is convenient as it ensures agreement between the measured and simulated hub-height turbulence intensity. It may, however, result in energy from scales that are not represented in the turbulence model being distributed on other frequencies. Furthermore, the approach is inappropriate if the centre of the turbulence field is not representative for the whole field.

In cases 2–5, the αϵ^2∕3 parameter is defined in such a way that the integral of the uu Mann-model spectrum equals the integral of the measured uu spectrum. For cases 2 and 3, the measured uu spectrum is obtained from the detrended wind speed measured by Mast3, whereas the pitot-tube-based wind speed is used for cases 4 and 5.

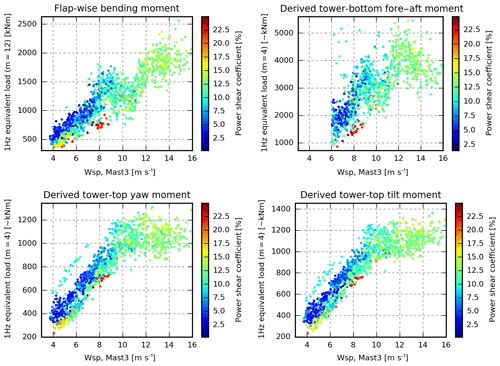
Figure 9 The 1 Hz equivalent loads coloured by the magnitude of the power shear coefficient extracted from the main met mast.

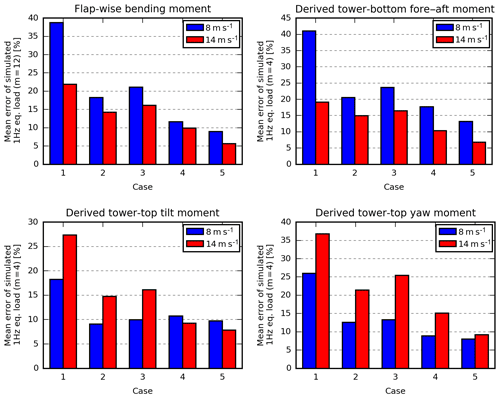
Figure 10 The 1 Hz equivalent loads coloured by a atmospheric stability classification metric (i.e. Monin–Obukhov length) extracted from the main met mast.

Due to the low fixed-position resolution of the pitot-tube wind speed, only the low frequency part of the uu spectrum can be obtained from the pitot tube, and this part is not suitable for fitting. Assuming that the turbulence field is homogeneous, the uu spectra are calculated from all of the pitot-tube observations after subtracting the position-dependent mean wind speed and trend. Due to the rotational sampling, the resulting spectra are very different from the fixed-position spectra with spectral peaks at the rotational speed and higher harmonics because the pitot tube moves in and out of turbulence structures. This phenomenon was addressed by Verholek (1978) and Hardesty et al. (1981) and theoretically explained by Kristensen and Frandsen (1982). The variance of the turbulence, i.e. the integral of the spectrum which is used in this context, is, however, independent of the frame of reference.

Figure 11 Mean relative error of the simulated equivalent loads.

In cases 3 and 5, the measured wind speeds are used as the input to a constraint turbulence simulator that modifies existing turbulence fields, e.g. stochastic realizations of the Mann turbulence model, to reproduce the specified wind speeds at the corresponding positions while preserving the statistics. The applied constraint turbulence simulation approach is described by Nielsen et al. (2003). In Case 3, the wind speed measured by Mast3 is used to constrain the turbulence at the position of Mast3, whereas the pitot-tube wind speed is used to constrain the turbulence in Case 5 at the instantaneous position of the rotating pitot tube.

5 Results and discussion

Figures 8, 9 and 10 show the equivalent loads coloured according to the magnitude of turbulence intensity, shear and atmospheric stability respectively. The strongest dependence on these three single parameters is seen in the flap and tower-bottom loads predominantly for low wind speeds, where the lowest loads are seen to occur under stable conditions with low turbulence intensity and high shear. The colours are, however, rather mixed, and wide areas have similar colours. Therefore, it is concluded that the scatter is to some degree independent of these three single parameters, and a more sophisticated approach, which considers the actual combination of inflow parameters, is required to predict the loads of specific periods.

Figure 12 Error distribution of the simulated equivalent loads.

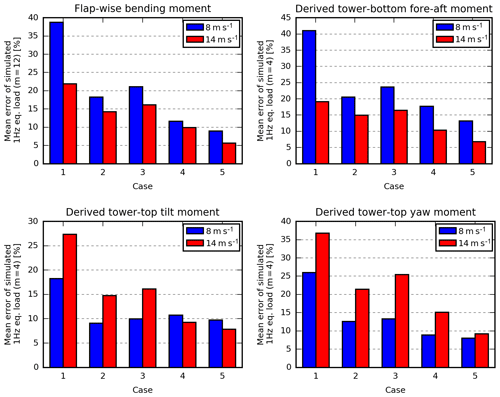
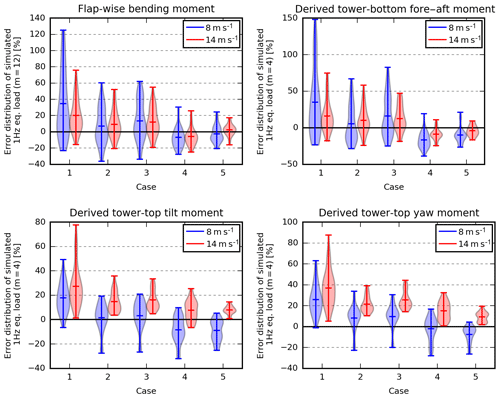
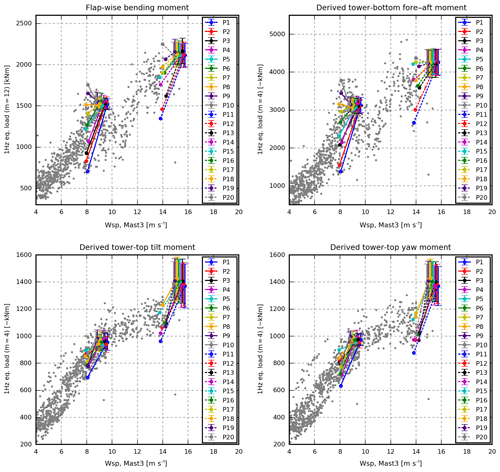
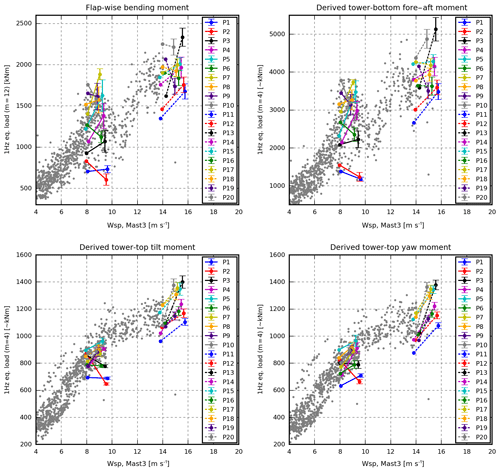
An overview of the mean relative error of the different cases can be found in Fig. 11, whereas Fig. 12 shows the distribution of the relative simulation errors. Figure 13 shows how to interpret Fig. 14–17, which offer more details regarding the cases by showing the measured and simulated loads of P1–P20.

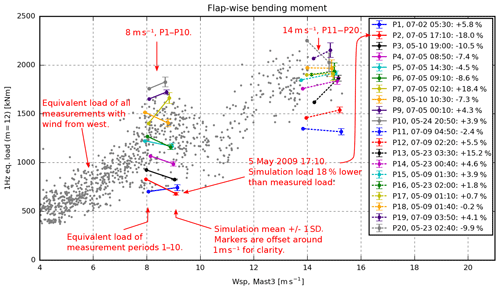
Figure 13 A schematic overview showing how to interpret Figs. 14–17. The figure shows the equivalent flap-wise bending moment of blade A. The grey dots represent the equivalent loads of all measurements with wind from the west, i.e. no-wake situations. The 20 selected periods, P1–P10 at 8 m s⁻¹ and P11–P20 at 14 m s⁻¹, are illustrated by dots connected to error bars. The dots show the measured equivalent load and wind speed, whereas the error bars illustrate the simulated mean loads ±1σ. Note that the error bars are offset around 1 m s⁻¹ to the right for clarity. The red dot and error bar, for instance, represent P2, i.e. 7 May 2019, 17:10–17:20 LT. The equivalent load measured in this period was around 830 kNm, whereas the six corresponding simulations had a mean load level around 682 kNm and a standard deviation of 16 kNm.

5.1 Case 1

In Case 1, only the wind speeds are different between the periods. Therefore, the load levels within the two wind-speed groups are very similar, as seen in Fig. 14. In this case, the simulated loads do not reflect the measured load variation; thus, the mean relative error seen in Fig. 11 is high, especially for the flap and tower-bottom loads at 8 m s⁻¹  where the relative variation is huge, but also in the tilt and yaw moments at 14 m s⁻¹  where the simulated loads are too high. It should also be noted that the variation of the simulations due to different turbulence realizations (seeds) does not reflect the measured variation, except for the yaw and tilt moments in the high-wind situations.

Figure 14 Case 1. Site average turbulence intensity and shear (wind-speed trend neglected). For interpretation see Fig. 13.

5.2 Case 2

In Case 2, information about the wind-speed trend, the measured turbulence level and the shear profile is included in the simulations.

Including the wind-speed trend increases the loads considerably in some periods. In P7, for example, the mean wind speed decreases 2.9 m s⁻¹ (linear fit) during the 10 min (see Table 2). Including this trend increases the flap and tower-bottom fatigue loads by around 30 %. This indicates that wind-speed trends are important to include in simulations for load validations.

In the selected periods, the turbulence intensity varies from 3.1 to 9.2 %. Including this information makes the range of the simulated loads reflect the range of the measured loads. The turbulence scaling approach, which is used for Case 1, is found to introduce substantial variation due to different turbulence realizations (seeds). This variation is considerably reduced in this and the succeeding cases by fitting the αϵ^2∕3 turbulence parameter. All things being equal, the αϵ^2∕3-fitting method reduces the average seed-induced variation of yaw loads at 14 m s⁻¹ from 450 to 90 kNm, while the maximum error of the tilt and yaw moments at 14 m s⁻¹ is approximately reduced from 80 % to 40 %.

The terrain is rather flat towards the west; therefore, the power shear exponents are modest (0.06 to 0.21) and are generally similar to the site-average values (0.09 for 8 m s⁻¹ and 0.13 for 14 m s⁻¹). The largest difference is found in P1, where the shear coefficient is increased from 0.09 to 0.21, which seen in isolation increases the simulated flap loads of this period by 9 %–18 %. In general, however, the effect of including the measured shear profile is limited, but the situation may be different if periods with wind from other directions were also considered or for extreme atmospheric stability conditions.

Furthermore, the stability dependent L and Γ parameters are used for the turbulence generation. Using these non-standard parameters, affects the flap and tower-bottom loads significantly in some periods. In P1 (stable conditions), the tower-bottom load decreases by 22 %, whereas it increases by 20 % in P11 (very unstable conditions). In these periods, however, the error of the simulated loads is not reduced.

Figure 11 reveals that the mean error of all loads is significantly reduced by utilizing these inflow characteristics. However, the correlation between the measured and simulated load levels is still poor. The simulated tower-bottom load of P5, for instance, is up to 67 % too high, and the measured tilt-moment fatigue loads of P2 and P5 are almost equal, even though they account for the minimum and maximum simulated loads respectively (see Fig. 15).

Figure 15 Case 2. Best case based on met-mast inflow information. For interpretation see Fig. 13.

5.3 Case 3

In Case 3, constraint turbulence simulation has been applied to constrain the turbulence to match the Mast3 wind-speed recordings at the position of Mast3, i.e. 250 m upstream. It has an effect on most of the simulated loads, but it slightly increases the mean error of all load sensors (see Fig. 11).

The biggest error increase is seen for P5, which has a distinct drop in the wind speed measured by Mast3 in the middle of the period. In the simulations, a similar drop, introduced by the constraint turbulence simulator, is unaffectedly advected with the steady mean wind to the turbine in agreement with Taylor's frozen turbulence hypothesis (Taylor, 1938). Around 30 s later, the same wind-speed drop subsequently hits the turbine and induces significant fatigue loads. In the real world, however, the turbulence structures change, the mean wind is not always steady and the wind-speed drop may even pass beside the turbine. In P5, a small drop is measured in the flap-wise bending moment, but it is only half the size of the simulated drop.

5.4 Case 4

Case 4 uses inflow characteristics extracted from the estimated free-stream pitot-tube wind speed. As seen in Table 2, these characteristics are different from the met-mast characteristics: the mean wind speed deviates up to 0.77 m s⁻¹, the wind-speed trend up to 1.45 m s⁻¹, the turbulence intensity up to 2.3 % and the power shear coefficient up to 0.11.

These mismatches are caused by the spatial distance between the locations of measurements, fundamental differences in the sensor technology and measurement method, and the uncertainties introduced in the conversion from pitot-tube measurement to free-stream wind speed in the fixed global coordinates (see Sect. 3.2).

Compared with Case 2 (the most equivalent met-mast case), all mean errors decrease by 5 % or more except the mean error of the tilt moment at 8 m s⁻¹ (see Fig. 11). The error ranges also decrease considerably for the flap and tower-bottom loads (see Fig. 12), whereas they are similar for the tilt- and yaw-moment error.

Figure 16 Case 4. Best case based on pitot-tube inflow information. For interpretation see Fig. 13.

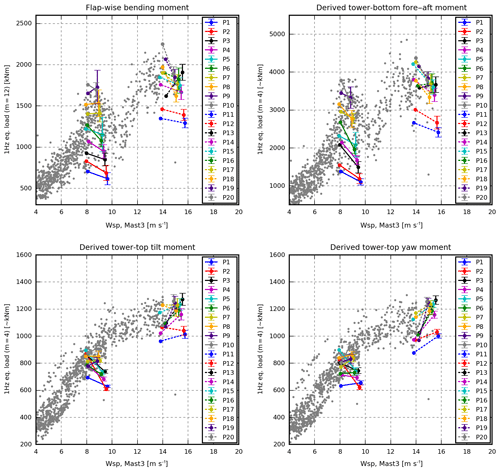
5.5 Case 5

In Case 5, the measured mean-wind-speed variations over the rotor area are modelled; furthermore, the instant measured pitot-tube wind speed is used to constrain the turbulence model.

Modelling the measured mean-wind-speed variations via the grid-based approach (exemplified in Fig. 7) increases all loads, except the yaw moments. In some periods, the flap load increases up to 15 %, and seen in isolation, the use of this approach slightly decreases the error of most of the simulated loads. It may be that the mismatch introduced by extrapolating the wind speed measured on the pitot-tube path to the whole rotor area almost neutralizes the positive effects, in which case more pitot tubes would be beneficial.

In this case, the turbulence field is generated using standard Mann turbulence L and Γ parameters and constraint turbulence simulation. In theory, this approach is problematic as the statistics of the applied constraints may be different from the standard parameters, such that the constraint turbulence simulator needs to compensate in other parts of the turbulence field to obtain the requested statistics. Using the stability-dependent L and Γ parameters instead has been tried. It was found to have a small positive effect on the errors at 8 m s⁻¹ and a similar small, but negative, effect on the errors at 14 m s⁻¹. Therefore, we have chosen to use the standard parameters in this case, to avoid the need for met-mast measurements to determine the stability conditions.

In the selected periods, the use of constraint turbulence simulation reduces the mean error for all load sensors. Furthermore, the range of the simulated loads due to different turbulence realizations decreases considerably, such that the need for multiple simulations with different seeds is reduced (see Fig. 17).

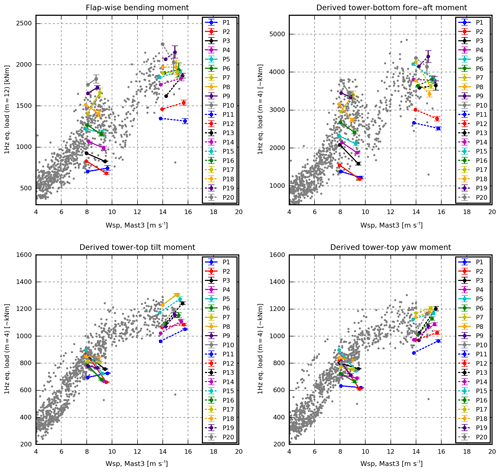
Figure 17 Case 5. Best case based on pitot-tube inflow information. For interpretation see Fig. 13.

In Case 5, the range of the simulated loads reflects the range of the measured loads. Therefore, they are assumed to be much more suitable for load extrapolation than the loads of Case 1.

The derived tower loads are slightly underestimated at 8 m s⁻¹ and overestimated at 14 m s⁻¹. These deviations may be introduced by the derivation of the synthetic tower loads (see Sect. 3.4), by the associated calibration of these uncertainties in the measured pitch-angle offsets, and by different control behaviour due to differences between the Siemens controller and the Basic DTU controller.

Only a few of the lines that connect the measured and simulated flap and tower-bottom observations intersect, meaning that the inflow conditions that result in high-load levels in the measurements also result in high-load levels in the simulations and vice versa. The same tendency is seen for the tilt and yaw moment at 14 m s⁻¹.

At the beginning of this section, it was concluded that an advanced approach that considers combinations of inflow parameters would be required to predict the loads of specific periods. Aeroelastic simulations can be considered to be such an approach, and to compare these simulations to the single parameter approach in Figs. 8, 9 and 10, two additional simulation sets were performed. Both sets comprise 970 simulations representing all suitable periods in the measurement database (one seed per period). In the first set, inflow information is extracted from the met masts (similar to Case 2), whereas the second set is based on information from the pitot tube (similar to Case 5). Figures 18 and 19 show the equivalent loads, coloured according to the HAWC2-simulated load relative to the wind-speed-dependent measured load range. This means that the red dots represent periods where the simulated load equals the maximum measured load at that wind speed, whereas the blue dots represent periods where the simulated load equals the minimum measured load. In other words, unmixed rainbow-coloured scatter means that the measured and simulated loads are similar and that the measured scatter can be predicted.

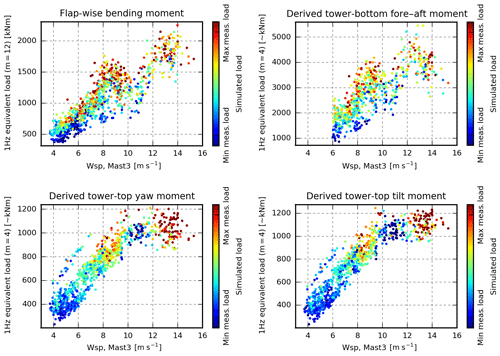
Figure 18 Equivalent measured loads, coloured by the corresponding simulation result. The simulations are performed using inflow information from the met masts similar to Case 2 (but only one seed per period). If the simulated load equals the maximum measured load at the current wind speed, then the observation is red, whereas observations where the simulated load equals the minimum load measured at the current wind speed are blue.

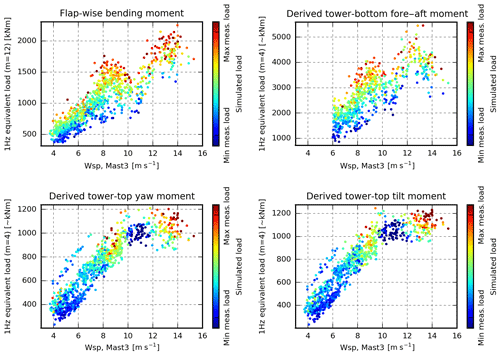
Figure 19 Equivalent measured loads, coloured by the corresponding simulation result. The simulations are performed using inflow information from the pitot tube, similar to Case 5 (but only one seed per period). If the simulated load equals the maximum measured load at the current wind speed, then the observation is red, whereas observations where the simulated load equals the minimum load measured at the current wind speed are blue.

The most promising result is seen in the flap and tower-bottom loads coloured according to the pitot-tube-based simulations (top row of Fig. 19) where the scatter is almost rainbow-coloured. This means that HAWC2 simulations with inflow characteristics extracted from the pitot tube are able to explain most of the measured flap and tower-bottom load scatter. The met-mast-based counterparts (top row of Fig. 18) are more mixed, even though most of the red observations are in the upper part of the scatter, and most of the blue observations are in the lower part.

The tilt and yaw moment scatter, in comparison, cannot be explained using these approaches. In both cases, most high-load observations are underestimated from 4 to 8 m s⁻¹ and from 10 to 12 m s⁻¹, whereas low-load observations are overestimated from 8 to 10 m s⁻¹ and above 12 m s⁻¹.

6 Conclusions

In this paper, different inflow information is extracted from a measurement database and used for aeroelastic simulations to investigate if using more detailed inflow descriptions improves the accuracy of the simulated loads.

The inflow information is extracted from nearby met masts and from a blade-mounted five-hole pitot tube. The pitot tube is located inside the induction zone, i.e. the measured flow velocity is influenced by the presence of the turbine. Therefore, an aerodynamic model is used to estimate the free-stream inflow velocity that would have been observed at the position of the pitot tube without the presence of the turbine.

In the case study, 20 periods, which represent a wide range of loads at mean wind speeds of 8 and 14 m s⁻¹, were selected. From these periods, inflow information was extracted for the simulations.

The case study revealed that the loads in simulations based on site-average turbulence intensity and shear profile (the typical load validation approach) did not reflect the measured loads, and most of the simulated load ranges were considerably smaller than the ranges of measured loads. Therefore, load extrapolation based on this approach may be misleading.

Including the met-mast measured turbulence intensity increases the variation of the simulated loads and makes the simulated load range reflect the measured range. However, the one-to-one correspondences were poor, with deviations up to 67 %.

The turbulence scaling approach, where the turbulence is scaled such that the turbulence intensity in the centre of the field matches the target intensity, was found to introduce a considerable variation in the simulated loads. Therefore, the scaling of the turbulence such that the integral of the target uu-spectrum matches the target variance is highly recommended.

In most periods, the inflow characteristics extracted from the pitot tube deviate from the inflow characteristics extracted from the met masts. These mismatches are caused by the spatial distance between the locations of met masts and the pitot tube, fundamental differences in the sensor technology and measurement method, and uncertainties introduced in the conversion from pitot-tube measurement to estimated free-stream inflow wind speed in fixed global coordinates.

Using the wind speed, turbulence intensity and shear measured by the blade-mounted pitot tube reduces the errors of the flap and tower-bottom loads in this study, whereas the errors of the tilt and yaw moments are similar. This indicates that it is beneficial to measure the inflow with a BMFS even though errors are introduced due to the dynamic and static deflection and torsion of the blade, as well as in the aerodynamic model that corrects for the turbine induction.

Including the measured wind-speed trend, shear profile, rotor-position-dependent variations in the mean wind and stability-dependent turbulence parameters were all found to change the loads significantly in some simulations, while the mean errors were only slightly affected. This information may, however, be important to include in other situations, e.g. half-wake situations and periods with high shear.

Constraint turbulence simulation was used to constrain the turbulence to match the instantaneously measured wind speeds at observation points. Constraining the turbulence to the wind speed measured by the met mast (250 m upstream) increased the errors of the simulated loads. In the simulations, a turbulence event introduced by the constraint turbulence simulator at the met-mast position is transported unaffected with the steady mean wind to the turbine, in agreement with Taylor's frozen turbulence hypothesis. In the real world, however, the turbulence structures change over time, and an upstream turbulence event may even pass beside the turbine. The event that hits the turbine in the simulation is thereby different from the event that hits the real turbine. Thus, it is not recommended to use constraint turbulence simulation based on wind speeds measured at a distance from the wind turbine.

Based on pitot-tube wind speed, however, constraint turbulence simulation reduces the mean error of all load sensors in this study. The final case is based on pitot-tube-derived mean wind speed, turbulence intensity and shear, and constraint turbulence simulation based on the pitot-tube-recorded wind speeds. In this case, the range of the simulated loads reflects the range of the measured loads. Therefore, it is more suitable for load extrapolation. Moreover, the sequences of the simulated and measured flap and tower-bottom loads are quite similar, meaning that the inflow conditions that result in high-load levels in the measurements in most cases also result in high-load levels in the simulations and vice versa. The same tendency is seen for the tilt and yaw moment at 14 m s⁻¹. In the final case, the range of the simulated loads due to different turbulence realizations (seeds) decreases considerably, meaning that the need for multiple simulations is reduced.

It was investigated if the enormous scatter that is seen, especially in the flap and tower-bottom loads, can be predicted by the turbulence intensity, shear profile or atmospheric stability conditions alone. The turbulence intensity explains some of the scatter, and the lowest loads are seen in stable conditions with low turbulence intensity and high shear. It is, however, concluded that a more sophisticated approach, which considers the actual combination of inflow parameters, is required to predict the loads of specific periods.

Aeroelastic simulations can be considered to be such an approach. Therefore, simulations representing all suitable periods have been performed based on inflow information from the met masts (wind speed, wind-speed trend, turbulence intensity and shear) and the pitot-tube recordings (wind speed, wind-speed trend, turbulence intensity, rotor-position-dependent shear and the instantaneously measured wind speed for constraint turbulence simulation). Based on these simulations, it is concluded that HAWC2 simulations based on inflow information from the pitot tube are able to predict the measured flap and tower-bottom load scatter very well in most periods. The met-mast-based simulations yield high loads for most periods in the upper half of the load scatter and vice versa, but the result is less impressive.

In both cases, the simulations cannot explain the tilt and yaw moment scatter, as most high-load observations are underestimated at some wind-speed ranges, and low-load observations are overestimated at other wind-speed ranges.