Optimal relationship between power and design-driving loads for wind turbine rotors using 1-D models

We investigate the optimal relationship between the aerodynamic power, thrust loading and size of a wind turbine rotor when its design is constrained by a static aerodynamic load. Based on 1-D axial momentum theory, the captured power $\stackrel{\mathrm{̃}}{P}$ for a uniformly loaded rotor can be expressed in terms of the rotor radius R and the rotor thrust coefficient C_T. Common types of static design-driving load constraints (DDLCs), e.g., limits on the permissible root-bending moment or tip deflection, may be generalized into a form that also depends on C_T and R. The developed model is based on simple relations and makes explorations of overall parameters possible in the early stage of the rotor design process. Using these relationships to maximize $\stackrel{\mathrm{̃}}{P}$ subject to a DDLC shows that operating the rotor at the Betz limit (maximum C_P) does not lead to the highest power capture. Rather, it is possible to improve performance with a larger rotor radius and lower C_T without violating the DDLC. As an example, a rotor design driven by a tip-deflection constraint may achieve 1.9 % extra power capture $\stackrel{\mathrm{̃}}{P}$ compared to the baseline (Betz limit) rotor.

This method is extended to the optimization of rotors with respect to annual energy production (AEP), in which the thrust characteristics C_T(V) need to be determined together with R. This results in a much higher relative potential for improvement since the constraint limit can be met over a larger range of wind speeds. For example, a relative gain in AEP of +5.7 % is possible for a rotor design constrained by tip deflections, compared to a rotor designed for optimal C_P. The optimal solution for AEP leads to a thrust curve with three distinct operational regimes and so-called thrust clipping.

1 Introduction

From the inception of the wind energy industry, it has been a clear trend that rotor sizes have been increasing. However, as discussed in Sieros et al. (2012), increasing the rotor size is not a clear way to decrease the cost of energy (CoE), since the rotor weight (closely related to rotor cost) will always scale with a larger exponent than the increase in power does. It is, therefore, argued that the lower CoE that has taken place is mostly due to improvements in technology. The turbine is structurally designed to carry loads coming from aerodynamics (steady or extreme) and the self-weight. Therefore, lowering the loads should lead to a lighter blade. The steady aerodynamic load is applied to extract power, and increasing the load leads to greater power production until the maximum power coefficient (max C_P) is reached. Increasing the load should lead to a heavier blade but it also leads to greater power production. It goes to show that understanding the relationship between loading, power production and structural response is very important for designing the most cost-effective turbine. This follows a trend occurring in recent years in which there is a belief that wind turbine optimization should include a more holistic approach, with concepts like multidisciplinary design analysis and optimization (MDAO) and systems engineering (Bottasso et al., 2012; Zahle et al., 2015; Fleming et al., 2016; and Perez-Moreno et al., 2016), where all of the parts of the turbine design that affect the cost should be taken into account along with the overall objective of minimizing the CoE. Some of these related works focus more on how the rotor loading affects the power and structural response. One of the concepts that comes out of this is the so-called low-induction rotor (LIR), in which the velocity induction at the rotor plane is lower than the value that maximizes the power coefficient. The concept was introduced by Chaviaropoulos and Sieros (2014) and it comes out of the optimization of annual energy production (AEP) by allowing the rotor to grow while constraining the flap root bending moment to be the same as some baseline. They state that the method can increase AEP by 3.5 % with a 10 % increase in the rotor radius, thereby showing that the LIR can increase AEP while keeping the same flap root bending moment. It agrees with Kelley (2017) who allowed for a change in the radial loading, resulting in a 5 % increase in AEP with a radius increase of 11 %. It was also investigated by Bottasso et al. (2015) who tested the potential of using the LIR both for AEP improvements with load constraints and as a cost-optimized rotor. They found the same results as the previous two investigations; the LIR can improve AEP, but when they consider the CoE they find that the LIR is not cost effective, meaning that the additional cost of extending the blade is not compensated by the increase in power. This conclusion is opposed to the conclusion made by Buck and Garvey (2015b) who set out to minimize the ratio between capital expenditures (CapEx) and AEP. They arrive at LIR as the optimal solution for minimizing CapEx/AEP, which is taken as a measure of CoE. Overall it seems that LIR can increase AEP while keeping the same load as a non-LIR baseline, but it is not clear if LIR is a cost-effective solution.

Another concept that is relevant in the context of this paper is thrust clipping (also known as peak shaving or force capping). For turbines, it is often the case that the maximum thrust is reached just before reaching the rated power, resulting in a so-called thrust peak. When using thrust clipping, this peak is lowered at the cost of power. It is used with many contemporary turbines for load alleviation but is often added as a feature after the design process. Buck and Garvey (2015a) made a design study in which they found that lowering the maximum thrust by 11 % leads to a 9 % reduction in material used, at the cost of 0.1 % less lifetime energy, resulting in an overall reduction of 0.2 % in the cost of energy. This shows that including thrust clipping in the design process can lead to a lower CoE.

In this paper, we investigate the relationship between the load, power and structural response of wind turbine rotors. Simple analytical models, based on 1-D aerodynamic momentum theory and Euler–Bernoulli beam theory, are introduced to establish the first-order relationship between these responses. This provides a useful framework for the initial rotor design, especially when high-level design parameters such as the rotor radius need to be fixed or there is a need to understand how load/structural responses will change with rotor size. The effect on the power curve and the related load/structural response with the variation in wind speeds is also investigated, which is useful for the initial design of the highly coupled aeroservoelastic rotor design problem.

The relatively simple models used in this paper do not capture the full complexity needed for detailed wind turbine rotor design and should be considered a tool for early-stage rotor design and overall exploration only. For example, the underlying theories (of 1-D aerodynamic momentum and Euler–Bernoulli beams) assume steady-state conditions, while designs are often constrained by load cases that are linked with extreme, unsteady or non-normal operational events, e.g., extreme turbulence, gusts, emergency shutdowns, subsystem faults or parked conditions. This is a limitation of the model developed here, but if there is a relation between the steady-state loads and the extreme loads, which is very likely, then the results are still valid.

As mentioned before, the overall target for current turbine design is to lower the CoE, but a cost model is not used, which is also a limitation of this study. However, cost models use several assumptions made in the design process such as the price of components in the design or composite lay-up of the blades, so a predicted cost will always be made with some uncertainty. Instead, load constraints are considered, much like in the above-mentioned LIR example. As was found by Bottasso et al. (2015), a constrained load might not lead to a lower CoE. So, to accommodate this, a constraint with a fixed mass is made, which is thought to be a better approximation of a fixed cost.

This study is carried out in order to obtain an overview of how the rotor design is more fundamentally influenced by different types of aerodynamic loading. Thus, an issue like the self-weight is important for modern turbines but is not directly included in this study; the static-mass moment especially has an impact on contemporary turbines. It could be included, but it was excluded to keep the study as simple as possible. Further discussion about the limitations and possible improvements of the study is given later in Sect. 4.5.

2 Theory

This section will introduce the variables and the basic relationships used in this paper. It is split into two subsections, in which Sect. 2.1 introduces aerodynamic variables, equations and the baseline rotor, while Sect 2.2 presents scaling laws used to formulate design-driving load constraints relative to the baseline rotor.

2.1 Aerodynamics

The theory underlying this Aerodynamics section is found in Sørensen (2016).

For wind turbine aerodynamics non-dimensional coefficients are often introduced and some of the common ones are for the rotor thrust (C_T) and power (C_P).

$$\begin{array}{}\text{(1)}& {\displaystyle }{C}_{\mathrm{T}}={\displaystyle \frac{T}{\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}^{\mathrm{2}}\mathit{\pi }{R}^{\mathrm{2}}}}\text{(2)}& {\displaystyle }{C}_{\mathrm{P}}={\displaystyle \frac{P}{\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}^{\mathrm{3}}\mathit{\pi }{R}^{\mathrm{2}}}},\end{array}$$

where T and P are the rotor thrust and power, respectively; ρ is the air density, V is the undisturbed flow speed and R is the rotor radius.

These definitions can be applied for any wind turbine rotor, but in this paper, we will use a simplified relationship between C_T and C_P that is derived from classical 1-D momentum theory. This implies an assumption of uniform aerodynamic loading across the rotor plane. The classical equations are often given in terms of the axial induction (a), which is defined as $a=\mathrm{1}-\frac{V_{\mathrm{rotor}}}{V}$, where V_rotor is the axial flow speed in the rotor plane. By combining the two classical momentum theory expressions for C_P(a) and C_T(a) (Sørensen, 2016, p. 11, Eq. 3.8), the relationship between these coefficients is arrived at as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& \left.\begin{array}{l}{C}_{\mathrm{T}}\left(a\right)=\mathrm{4}a(\mathrm{1}-a)\\ C_{\mathrm{P}}\left(a\right)=\mathrm{4}a(\mathrm{1}-a{)}^{\mathrm{2}}\end{array}\right\}\Rightarrow C_{\mathrm{P}}\left(C_{\mathrm{T}}\right)=(\mathrm{1}-a)C_{\mathrm{T}}\\ & ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}},C_{\mathrm{T}}\in [\mathrm{0},\mathrm{1}],\end{array}\end{array}$$

where a(C_T) is found by inverting C_T(a) and using the negative solution. A plot of C_T vs. C_P can be seen in Fig. 1. This C_P(C_T) curve is monotonically decreasing in slope and reaches a maximum of $C_{\mathrm{P}}=\mathrm{16}/\mathrm{27}$, corresponding to the well-known Betz limit at $C_{\mathrm{T}}=\mathrm{8}/\mathrm{9}$. These monotonicity properties lead to the key observation that a reduction in thrust ($C_{\mathrm{T}}=\mathrm{8}/\mathrm{9}-\mathrm{\Delta }{C}_{\mathrm{T}}$) will not lead to a proportional change in power (ΔC_P). This motivates the investigation in this paper of the trade-off between power and loads.

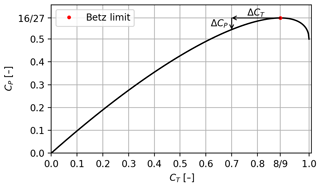
Figure 1 Relationship between normalized rotor load C_T and power coefficient C_P from 1-dimensional momentum theory. Note that around the Betz limit a small change in C_T does not lead to a proportional change in C_P; this is illustrated by ΔC_T and ΔC_P.

2.1.1 Power capture and annual energy production (AEP)

One way to understand the power yield of a rotor is to consider Eq. (2) as consisting of three separate terms as follows:

$$\begin{array}{}\text{(4)}& P=\underset{\mathrm{Wind}}{\underbrace{{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }{V}^{\mathrm{3}}}}\cdot \underset{\mathrm{Size}}{\underbrace{{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\pi }{R}^{\mathrm{2}}}}\cdot \underset{\mathrm{Coefficient}}{\underbrace{{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{C}_{\mathrm{P}}}}.\end{array}$$

“Wind” is the part of the equation that depends on the wind conditions, “size” is the part of the equation that depends on the rotor-swept area and “coefficient” is the part of the equation related to the power coefficient, representing the capability of the rotor to extract power from the wind. The combination of Eqs. (2) and (3) provides an expression that captures the last two terms, which are the only ones affected by the design of the turbine; the result is as follows:

$$\begin{array}{}\text{(5)}& \stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}},\stackrel{\mathrm{̃}}{R}\right)={\displaystyle \frac{P}{\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}^{\mathrm{3}}\mathit{\pi }{R}_{\mathrm{0}}^{\mathrm{2}}}}=C_{\mathrm{P}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}},\end{array}$$

where $\stackrel{\mathrm{̃}}{R}$ equals R∕R₀, with R₀ being the radius of the baseline rotor. This equation will be referred to as the power capture equation. It shows that power can be changed by changing either the loading (C_T) or the rotor radius (R). This will serve as the basic equation when the power capture is optimized for a single design point.

When considering turbine design over the range of operational conditions, annual energy production (AEP) is introduced as an integral metric representing the energy produced per year given some wind speed frequency distribution. It can be computed as the power production (P) weighted by the probability density of wind speeds (PDF_wind) multiplied by the period of 1 year (T_year) as follows:

$$\begin{array}{}\text{(6)}& \mathrm{AEP}=T_{\mathrm{year}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }\mathit{\pi }{R}_{\mathrm{0}}^{\mathrm{2}}\underset{V_{\mathrm{CI}}}{\overset{V_{\mathrm{CO}}}{\int }}\stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}}\left(V\right),\stackrel{\mathrm{̃}}{R}\right)\cdot V^{\mathrm{3}}\cdot {\mathrm{PDF}}_{\mathrm{wind}}\left(V\right)\mathrm{d}V.\end{array}$$

The wind speed probability distribution PDF_wind will be described with a Weibull distribution. V_CI and V_CO are the wind speeds for cut in and cut out during wind turbine operation. Here they are taken to be V_CI=3 m s⁻¹ and V_CO=25 m s⁻¹, which are common numbers for modern wind turbines.

In this paper, we will use a dimensionless measure for AEP which is equivalent to the so-called capacity factor, defined as follows:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}\stackrel{\mathrm{̃}}{\mathrm{AEP}}& \left(C_{\mathrm{T}},\stackrel{\mathrm{̃}}{R}\right)={\displaystyle \frac{\mathrm{AEP}}{T_{\mathrm{year}}{P}_{\mathrm{rated}}}}={\displaystyle \frac{\mathrm{AEP}}{T_{\mathrm{year}}\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }\mathit{\pi }{R}_{\mathrm{0}}^{\mathrm{2}}\frac{\mathrm{16}}{\mathrm{27}}{V}_{\mathrm{0}}^{\mathrm{3}}}}\\ & ={\displaystyle \frac{\mathrm{27}}{\mathrm{16}}}\underset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CI}}}{\overset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CO}}}{\int }}\stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}}\left(\stackrel{\mathrm{̃}}{V}\right),\stackrel{\mathrm{̃}}{R}\right)\cdot {\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}\cdot {\mathrm{PDF}}_{\mathrm{wind}}\left(\stackrel{\mathrm{̃}}{V}\right)\mathrm{d}\stackrel{\mathrm{̃}}{V}.\end{array}\end{array}$$

$\stackrel{\mathrm{̃}}{V}$ is a normalized wind speed given by $V=\stackrel{\mathrm{̃}}{V}{V}_{\mathrm{0}}$, where V₀ is the wind speed at which the turbine reaches the rated power (P_rated). Throughout this paper it is taken to be V₀=10 m s⁻¹. It should further be noted that PDF_winddV is dimensionless and by nondimensionalizing AEP it also follows that PDF${}_{\mathrm{wind}}d\stackrel{\mathrm{̃}}{V}$ is dimensionless. Throughout this paper $\stackrel{\mathrm{̃}}{\mathrm{AEP}}$ is calculated using a discretization of the integral, which is computed using the trapezoidal rule given as $\underset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CI}}}{\overset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CO}}}{\int }}f(\stackrel{\mathrm{̃}}{V};C_{\mathrm{T}},\stackrel{\mathrm{̃}}{R})d\stackrel{\mathrm{̃}}{V}\approx \sum _{i=\mathrm{1}}^N\frac{f({\stackrel{\mathrm{̃}}{V}}_{i+\mathrm{1}};C_{\mathrm{T}},\stackrel{\mathrm{̃}}{R})+f({\stackrel{\mathrm{̃}}{V}}_i;C_{\mathrm{T}},\stackrel{\mathrm{̃}}{R}))}{\mathrm{2}}\mathrm{\Delta }{\stackrel{\mathrm{̃}}{V}}_i$, where the discretization (N) was found to become insignificant for N=200.

2.1.2 Baseline rotor

The work here aims to demonstrate an improved rotor performance compared to a baseline design. This baseline design is chosen to be a turbine operating at the Betz limit below the rated wind speed and keeping a constant power above the rated power.

$$\begin{array}{}\text{(8)}& C_{\mathrm{T},\mathrm{0}}={\displaystyle \frac{\mathrm{8}}{\mathrm{9}}}\approx \mathrm{0.889};C_{\mathrm{P},\mathrm{0}}={\displaystyle \frac{\mathrm{16}}{\mathrm{27}}}\approx \mathrm{0.593}\end{array}$$

This choice of baseline mimics the typical practice of designing wind turbines target operation at the maximum C_P below the rated power. In reality, turbines will not achieve a maximum C_P at $C_{\mathrm{T}}=\mathrm{8}/\mathrm{9}$ since losses alter the relationship between C_T and C_P, but this does not change the fact that turbines are operated at the point of the maximum C_P. Figure 2 shows the power and thrust curves for the baseline rotor.

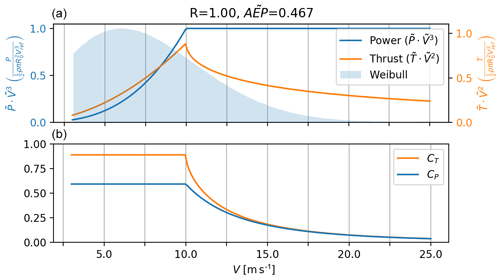
Figure 2 (a) The dimensionless power and thrust for the baseline rotor as a function of wind speed. Overlaid (in blue) is the Weibull wind speed frequency distribution used throughout (IEC-class III: V_avg=7.5; k=2). (b) C_T and C_P as a functions of wind speed. These curves reflect how most turbines are operated today, targeting the maximum power coefficient below the rated power, which leads to a thrust peak just before the rated power.

In this paper, all results are presented as the change in performance relative to that of the baseline rotor. For this reason, all of the relevant variables (denoted with a zero in the subscript) will be normalized by the corresponding baseline rotor values.

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }R={\displaystyle \frac{R}{R_{\mathrm{0}}}}-\mathrm{1}\text{(10)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }\stackrel{\mathrm{̃}}{P}={\displaystyle \frac{C_{\mathrm{P}}{R}^{\mathrm{2}}}{C_{\mathrm{P},\mathrm{0}}{R}_{\mathrm{0}}^{\mathrm{2}}}}-\mathrm{1}\text{(11)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }\stackrel{\mathrm{̃}}{L}={\displaystyle \frac{C_{\mathrm{T}}{R}^{L_{\exp }}}{C_{\mathrm{T},\mathrm{0}}{R}_{\mathrm{0}}^{L_{\exp }}}}-\mathrm{1}\text{(12)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }\stackrel{\mathrm{̃}}{\mathrm{AEP}}={\displaystyle \frac{\stackrel{\mathrm{̃}}{\mathrm{AEP}}}{{\stackrel{\mathrm{̃}}{\mathrm{AEP}}}_{\mathrm{0}}}}-\mathrm{1},\end{array}$$

where $\stackrel{\mathrm{̃}}{L}$ as well as L_exp is a generalized load that is introduced in Sect. 4.1 (Effects on loads), and it is written here for later reference.

2.2 Scale laws and constraints for design-driving loads

In this section, examples of static aerodynamic design-driving loads (DDLs) will be presented. These examples are not meant to be exhaustive but include several of the key considerations that constrain the practical design of wind turbine rotors. From the scaled loads, design-driving load constraints (DDLCs) are introduced, which limit loads so that these do not exceed the levels of the baseline rotor. Based on the DDL examples, it is shown that DDLCs can be elegantly put in a generalized form.

2.2.1 Thrust (T)

Thrust typically does not limit the design of the rotor itself but more likely is a constraint imposed from the design of the tower and/or foundation. The thrust scaling and the associated DDLC is given by

$$\begin{array}{}\text{(13)}& \begin{array}{l}\mathrm{Scaling}\\ T=\frac{\mathrm{1}}{\mathrm{2}}\mathit{\rho }{V}_{\mathrm{0}}^{\mathrm{2}}\mathit{\pi }{R}^{\mathrm{2}}{C}_{\mathrm{T}}\end{array}\Rightarrow \begin{array}{l}\mathrm{DDLC}\\ \left(T\right)=\frac{T}{T_{\mathrm{0}}}=\frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}{\left(\frac{R}{R_{\mathrm{0}}}\right)}^{\mathrm{2}}\le \mathrm{1}.\end{array}\end{array}$$

2.2.2 Root flap bending moment (M_flap)

The root flap moment is the bending moment at the rotational center in the axial flow direction. To compute M_flap, the 1-D momentum theory relations for infinitesimal thrust (dT) and moment (dM) are integrated; they are first expressed as

$$\begin{array}{}\text{(14)}& {\displaystyle }& {\displaystyle }\mathrm{d}T={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }{V}^{\mathrm{2}}{C}_{\mathrm{T}}\mathrm{2}\mathit{\pi }r\mathrm{d}r\text{(15)}& {\displaystyle }& {\displaystyle }\mathrm{d}{M}_{\mathrm{flap}}=r\mathrm{d}T,\end{array}$$

where r is the radius location of the infinitesimal load ($r\in [\mathrm{0},R]$). The moment scaling and DDLC can be found as follows:

$$\begin{array}{}\text{(16)}& \begin{array}{l}\mathrm{Scaling}\\ M_{\mathrm{flap}}={\int }_{\mathrm{0}}^R\mathrm{d}{M}_{\mathrm{flap}}=\frac{\mathrm{1}}{\mathrm{3}}\mathit{\rho }{V}_{\mathrm{0}}^{\mathrm{2}}{C}_{\mathrm{T}}\mathit{\pi }{R}^{\mathrm{3}}\end{array}\Rightarrow \begin{array}{l}\mathrm{DDLC}\\ \left(M_{\mathrm{flap}}\right)=\frac{M_{\mathrm{flap}}}{M_{\mathrm{flap},\mathrm{0}}}=\frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}{\left(\frac{R}{R_{\mathrm{0}}}\right)}^{\mathrm{3}}\le \mathrm{1}.\end{array}\end{array}$$

As shown, M_flap scales with R³ so it grows faster than the power, which scales as R². M_flap is important for the blade design since the flap-wise aerodynamic loads need to be transferred via the blade structure to the root of the blade.

2.2.3 Tip deflection (δ_tip)

Tip deflection is a common DDLC for contemporary utility-scale turbines, where tip clearance between tower and blade may become critical because of the relatively long and slender blades. To get an idea of how tip-deflection scales with changes in loading and rotor radius Euler–Bernoulli beam theory; (Bauchau and Craig, 2009, p. 189, Eq. 5.40) is used. For the problem here, it takes the form of

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}}{\mathrm{d}{r}^{\mathrm{2}}}}EI{\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}\mathit{\delta }}{\mathrm{d}{r}^{\mathrm{2}}}}={\displaystyle \frac{\mathrm{d}T}{\mathrm{d}r}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }{V}^{\mathrm{2}}{C}_{\mathrm{T}}\mathrm{2}\mathit{\pi }r,\end{array}$$

where δ is the deflection in the flap-wise direction of the blade at location r. EI is the stiffness of the blade at location r. For modern turbines the stiffness decrease towards the tip of the blade. To get an estimate for the stiffness, it is assumed that stiffness follows the size of the chord (EI∝c). The chord is given by the equation in Sørensen (2016, p. 68, Eq. 5.26); with an approximation for the outer part of the blade it can be found that $c\propto R/r$ which means that $EI\propto R/r$. An approximate model for EI that has $EI\propto R/r$ can be made,

$$\begin{array}{}\text{(18)}& EI\left(r\right)={\displaystyle \frac{E{I}_{\mathrm{r}}}{\mathrm{1}+\left(\frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}-\mathrm{1}\right)\frac{r}{R}}},\end{array}$$

where EI_r is the stiffness at the root and EI_t is the stiffness at the tip of the blade. As mentioned above for wind turbines EI_r>EI_t.

With the equation for EI, Eq. (17) can be solved by indefinite integration, with the integration constants determined from the following boundary conditions:

$$\begin{array}{}\text{(19)}& \begin{array}{rl}& \underset{\mathrm{Clamped}\mathrm{root}}{\underbrace{\mathit{\delta }(r=\mathrm{0})=\mathrm{0},{\displaystyle \frac{\mathrm{d}\mathit{\delta }}{\mathrm{d}r}}(r=\mathrm{0})=\mathrm{0}}}\\ & \underset{\mathrm{Free}\mathrm{tip}}{\underbrace{{\displaystyle \frac{{\mathrm{d}}^{\mathrm{2}}\mathit{\delta }}{\mathrm{d}{r}^{\mathrm{2}}}}(r=R)=\mathrm{0},{\displaystyle \frac{{\mathrm{d}}^{\mathrm{3}}\mathit{\delta }}{\mathrm{d}{r}^{\mathrm{3}}}}(r=R)=\mathrm{0}}}.\end{array}\end{array}$$

The resulting displacement solution becomes

$$\begin{array}{}\text{(20)}& {\displaystyle }\begin{array}{rl}\mathit{\delta }& ={\displaystyle \frac{\mathrm{11}\mathit{\pi }}{\mathrm{120}}}{\displaystyle \frac{V^{\mathrm{2}}\mathit{\rho }}{E{I}_{\mathrm{r}}}}{C}_{\mathrm{T}}{R}^{\mathrm{5}}\left({\displaystyle \frac{\mathrm{2}}{\mathrm{33}}}\left({\displaystyle \frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}}-\mathrm{1}\right){\stackrel{\mathrm{̃}}{r}}^{\mathrm{6}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{11}}}{\stackrel{\mathrm{̃}}{r}}^{\mathrm{5}}\right.\\ & \left.-{\displaystyle \frac{\mathrm{5}}{\mathrm{11}}}\left({\displaystyle \frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}}-\mathrm{1}\right){\stackrel{\mathrm{̃}}{r}}^{\mathrm{4}}+{\displaystyle \frac{\mathrm{10}}{\mathrm{11}}}\left({\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\displaystyle \frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}}-{\displaystyle \frac{\mathrm{5}}{\mathrm{3}}}\right){\stackrel{\mathrm{̃}}{r}}^{\mathrm{3}}+{\displaystyle \frac{\mathrm{20}}{\mathrm{11}}}{\stackrel{\mathrm{̃}}{r}}^{\mathrm{2}}\right)\end{array}\text{(21)}& {\displaystyle }={\displaystyle \frac{\mathrm{11}\mathit{\pi }}{\mathrm{120}}}{\displaystyle \frac{V^{\mathrm{2}}\mathit{\rho }}{E{I}_{\mathrm{r}}}}{C}_{\mathrm{T}}{R}^{\mathrm{5}}{\mathit{\delta }}_{\mathrm{shape}}\left(\stackrel{\mathrm{̃}}{r},{\displaystyle \frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}}\right),\end{array}$$

where the normalized radius ($\stackrel{\mathrm{̃}}{r}\in [\mathrm{0},\mathrm{1}]$) has been introduced so that $r=R\cdot \stackrel{\mathrm{̃}}{r}$. The polynomial shape of the deflection has been collected in δ_shape. The maximum deflection occurs at the blade tip ($\stackrel{\mathrm{̃}}{r}=\mathrm{1}$), which leads to a scaling relation and DDLC for tip deflection:

$$\begin{array}{}\text{(22)}& \begin{array}{rl}& \begin{array}{l}\mathrm{Scaling}\\ {\mathit{\delta }}_{\mathrm{tip}}=\frac{\mathrm{11}\mathit{\pi }}{\mathrm{120}}\frac{V^{\mathrm{2}}\mathit{\rho }}{E{I}_{\mathrm{r}}}{C}_{\mathrm{T}}{R}^{\mathrm{5}}{\mathit{\delta }}_{\mathrm{shape}}\left(\stackrel{\mathrm{̃}}{r}=\mathrm{1},\frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}\right)\end{array}\\ & \Rightarrow \begin{array}{l}\mathrm{DDLC}\\ \left({\mathit{\delta }}_{\mathrm{tip}}\right)=\frac{{\mathit{\delta }}_{\mathrm{tip}}}{{\mathit{\delta }}_{\mathrm{tip},\mathrm{0}}}=\frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}{\left(\frac{R}{R_{\mathrm{0}}}\right)}^{\mathrm{5}}\le \mathrm{1},\end{array}\end{array}\end{array}$$

where it has been implicitly assumed that any change in stiffness needs to follow

$$\begin{array}{}\text{(23)}& {\displaystyle \frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}}={\displaystyle \frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{r},\mathrm{0}}}}\left({\displaystyle \frac{E{I}_{\mathrm{r},\mathrm{0}}}{E{I}_{\mathrm{t},\mathrm{0}}}}+{\displaystyle \frac{\mathrm{26}}{\mathrm{7}}}\right)-{\displaystyle \frac{\mathrm{26}}{\mathrm{7}}},\end{array}$$

with the simplest way to satisfy this relation being that $E{I}_{\mathrm{r}}=E{I}_{\mathrm{r},\mathrm{0}}$, which gives $\frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}=\frac{E{I}_{\mathrm{r},\mathrm{0}}}{E{I}_{\mathrm{t},\mathrm{0}}}$.

2.2.4 Tip deflection with constant mass

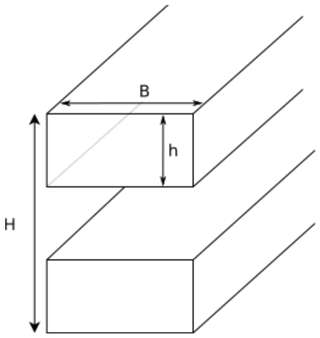
The final example of a DDL is also based on tip deflection but includes a condition to maintain a constant mass of the load-carrying structure of the blade. To this end, the stylized spar-cap layout depicted in Fig. 3 is assumed. This layout consists of two planks. The stiffness of a spar-cap structure with a homogeneous Young's modulus (E) can be found from the stiffness of the rectangle and the parallel axis theorem (see Fig. 3 for the variable definitions) as follows:

$$\begin{array}{}\text{(24)}& \begin{array}{rl}& \left.\begin{array}{l}{I}_{\mathrm{rect}}=\frac{B{h}^{\mathrm{3}}}{\mathrm{12}}\\ EI=\mathrm{2}E\left(I_{\mathrm{rect}}+A{\left(\frac{H-h}{\mathrm{2}}\right)}^{\mathrm{2}}\right)\\ A=Bh\end{array}\right\}\\ & EI=\mathrm{2}E\left({\displaystyle \frac{B{h}^{\mathrm{3}}}{\mathrm{12}}}+Bh{\left({\displaystyle \frac{H-h}{\mathrm{2}}}\right)}^{\mathrm{2}}\right)\\ & =E{\displaystyle \frac{H^{\mathrm{2}}Bh}{\mathrm{2}}}\left({\displaystyle \frac{h^{\mathrm{2}}}{\mathrm{3}{H}^{\mathrm{2}}}}+{\left(\mathrm{1}-{\displaystyle \frac{h}{H}}\right)}^{\mathrm{2}}\right).\end{array}\end{array}$$

For modern wind turbines $h/H\ll \mathrm{1}$, meaning that a common approximation is

$$\begin{array}{}\text{(25)}& EI\approx E{\displaystyle \frac{H^{\mathrm{2}}Bh}{\mathrm{2}}}.\end{array}$$

To compute the mass for such a structure it will be assumed that plank height h and the plank width B are constant and the change in EI comes from a decrease in building height H. Then, if h is decreased when R is increased, the following relationship needs to be satisfied for the mass of the planks to be constant (assuming a constant mass density),

$$\begin{array}{}\text{(26)}& Rh=R_{\mathrm{0}}{h}_{\mathrm{0}}.\end{array}$$

From there it follows that changes in the radius of the rotor will change the stiffness as

$$\begin{array}{}\text{(27)}& \left.\begin{array}{l}EI\approx E\frac{H^{\mathrm{2}}Bh}{\mathrm{2}}\left(\mathrm{25}\right)\\ h=\frac{R_{\mathrm{0}}{h}_{\mathrm{0}}}{R}\left(\mathrm{26}\right)\end{array}\right\}EI\approx E{\displaystyle \frac{H^{\mathrm{2}}B{R}_{\mathrm{0}}{h}_{\mathrm{0}}}{\mathrm{2}R}}.\end{array}$$

Combining this equation with the tip deflection equation (Eq. 21), scaling and DDLC can be found as follows:

$$\begin{array}{}\text{(28)}& \begin{array}{rl}& \begin{array}{l}\mathrm{Scaling}\\ \left.\begin{array}{l}{\mathit{\delta }}_{\mathrm{tip}}=\frac{\mathrm{11}\mathit{\pi }}{\mathrm{120}}\frac{V^{\mathrm{2}}\mathit{\rho }}{E{I}_{\mathrm{r}}}{C}_{\mathrm{T}}{R}^{\mathrm{5}}{\mathit{\delta }}_{\mathrm{shape}}\left(\stackrel{\mathrm{̃}}{r}=\mathrm{1},\frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}\right)\\ EI\approx E\frac{H^{\mathrm{2}}B{R}_{\mathrm{0}}{h}_{\mathrm{0}}}{\mathrm{2}R}\end{array}\right\}\end{array}\\ & \Rightarrow \begin{array}{l}\mathrm{DDLC}\\ \left({\mathit{\delta }}_{\mathrm{tip}+\mathrm{mass}}\right)=\frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}\frac{E{I}_{\mathrm{r},\mathrm{0}}}{E{I}_{\mathrm{r}}}{\left(\frac{R}{R_{\mathrm{0}}}\right)}^{\mathrm{5}}=\frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}{\left(\frac{R}{R_{\mathrm{0}}}\right)}^{\mathrm{6}}\le \mathrm{1},\end{array}\end{array}\end{array}$$

with the use of the fact that changing h by the same magnitude for the whole blade leads to $\frac{E{I}_{\mathrm{r}}}{E{I}_{\mathrm{t}}}=\frac{E{I}_{\mathrm{r},\mathrm{0}}}{E{I}_{\mathrm{t},\mathrm{0}}}$ and thereby does not affect δ_shape. It should be noted that choosing B to change instead will lead to the same scaling but the difference is that changing the plank thickness might lead to higher-order effects, although they are expected to be insignificant.

Figure 3 Assumed spar-cap structure with dimensions: H is the total build height, h is the space between planks and B is the plank width.

2.2.5 Generalizing the constraint form

Considering the four DDLC examples presented above, there appears to be a pattern in the scaling relations that may be written as follows:

$$\begin{array}{}\text{(29)}& {\displaystyle \frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}}{\left({\displaystyle \frac{R}{R_{\mathrm{0}}}}\right)}^{R_{\exp }}\le \mathrm{1},\end{array}$$

where R_exp is the exponent of R in the DDLC.

If the constraint limit is met, the following relationship can be written

$$\begin{array}{}\text{(30)}& R=R_{\mathrm{0}}{\left({\displaystyle \frac{C_{\mathrm{T},\mathrm{0}}}{C_{\mathrm{T}}}}\right)}^{\frac{\mathrm{1}}{R_{\exp }}}.\end{array}$$

3 Formulation of rotor design problems

Based on the performance and constraint relationships outlined in the previous section, this section will present the formulation for rotor design as optimization problems. Two different classes of problems are introduced, namely power-capture optimization and AEP optimization, where the latter is a generalization of the former with the constraint depending on the wind speed.

3.1 Power-capture optimization

The optimization problem can be stated as

$$\begin{array}{}\text{(31)}& {\displaystyle }& {\displaystyle }\underset{C_{\mathrm{T}},\stackrel{\mathrm{̃}}{R}}{\mathrm{maximize}}\stackrel{\mathrm{̃}}{P}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}}\text{(32)}& {\displaystyle }& {\displaystyle }\mathrm{subject}\mathrm{to}{\displaystyle \frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}}{\stackrel{\mathrm{̃}}{R}}^{R_{\exp }}\le \mathrm{1},\end{array}$$

where the definition of $\stackrel{\mathrm{̃}}{R}=R/R_{\mathrm{0}}$ has been used for consistency. The solution for this optimization problem is presented in Sect. 4.1.

It should be noted that this optimization problem is similar to the problem that is given by Chaviaropoulos and Sieros (2014) in which they optimize while keeping M_flap. So the optimization problem in this paper is a generalization of their optimization problem.

3.2 AEP optimization

In contrast to the above mentioned optimization of power capture, optimization with respect to AEP requires the determination of $C_{\mathrm{T}}\left(\stackrel{\mathrm{̃}}{V}\right)$, so it involves a function opposed to a scalar value. It is also necessary to set the rated power to constant value, while the wind speed at which the rated power is reached is allowed to change. The problem can be formulated as

$$\begin{array}{}\text{(33)}& {\displaystyle }\underset{C_{\mathrm{T}}\left(\stackrel{\mathrm{̃}}{V}\right),\stackrel{\mathrm{̃}}{R}}{\mathrm{maximize}}\stackrel{\mathrm{̃}}{\mathrm{AEP}}={\displaystyle \frac{\mathrm{27}}{\mathrm{16}}}\underset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CI}}}{\overset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CO}}}{\int }}\stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}}\left(\stackrel{\mathrm{̃}}{V}\right),\stackrel{\mathrm{̃}}{R}\right)\cdot {\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}\cdot {\mathrm{PDF}}_{\mathrm{wind}}\left(\stackrel{\mathrm{̃}}{V}\right)\mathrm{d}\stackrel{\mathrm{̃}}{V}\text{(34)}& {\displaystyle }\mathrm{subject}\mathrm{to}\begin{array}{ll}{\stackrel{\mathrm{̃}}{V}}^{\mathrm{2}}\frac{C_{\mathrm{T}}\left(\stackrel{\mathrm{̃}}{V}\right)}{C_{\mathrm{T},\mathrm{0}}}{\stackrel{\mathrm{̃}}{R}}^{R_{\exp }}\le \mathrm{1};& \left(\mathrm{DDLC}\right)\\ \frac{\mathrm{27}}{\mathrm{16}}\stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}}\left(\stackrel{\mathrm{̃}}{V}\right),\stackrel{\mathrm{̃}}{R}\right){\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}\le \mathrm{1}& \left(\mathrm{rated}\mathrm{power}\right),\end{array}\end{array}$$

where the wind speed scaling has been added to the DDLC.

4 Results and discussion

This section discusses the solutions to the rotor design optimization problems introduced in the previous section.

4.1 Optimizing for power capture

The constrained optimization problem maximizing power capture, as stated in Sect. 3, may be simplified based on the observation that optimum solutions will occur at the DDL constraint limit. To understand this, consider that the power capture of a rotor with an inactive constraint may always be improved by scaling the rotor up until the constraint is met. This is true irrespective of the DDLC that determines the rotor design. Hence, an explicit relation $\stackrel{\mathrm{̃}}{R}\left(C_{\mathrm{T}}\right)$ can be used to reformulate the problem from a constrained optimization problem in two variables to an unconstrained optimization problem in one variable.

$$\begin{array}{}\text{(35)}& \begin{array}{rl}& \left.\begin{array}{l}\stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}},\stackrel{\mathrm{̃}}{R}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}}\left(\mathrm{5}\right)\\ \stackrel{\mathrm{̃}}{R}={\left(\frac{C_{\mathrm{T},\mathrm{0}}}{C_{\mathrm{T}}}\right)}^{\frac{\mathrm{1}}{R_{\exp }}}\left(\mathrm{30}\right)\end{array}\right\}\\ & \Rightarrow \stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}}\right)={\displaystyle \frac{C_{\mathrm{T},\mathrm{0}}^{\mathrm{2}\frac{\mathrm{1}}{R_{\exp }}}}{\mathrm{2}}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}^{\mathrm{1}-\mathrm{2}\frac{\mathrm{1}}{R_{\exp }}},\end{array}\end{array}$$

with the optimization problem now as follows:

$$\begin{array}{}\text{(36)}& \underset{C_{\mathrm{T}}}{\mathrm{maximize}}\stackrel{\mathrm{̃}}{P}={\displaystyle \frac{C_{\mathrm{T},\mathrm{0}}^{\mathrm{2}\frac{\mathrm{1}}{R_{\exp }}}}{\mathrm{2}}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}^{\mathrm{1}-\mathrm{2}\frac{\mathrm{1}}{R_{\exp }}}.\end{array}$$

By differentiating the objective function (Eq. 35 with respect to C_T and finding its root, the optimal C_T as a function of R_exp is arrived at.

$$\begin{array}{}\text{(37)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}\stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}}\right)}{\mathrm{d}{C}_{\mathrm{T}}}}=\mathrm{0}\Rightarrow \text{(38)}& {\displaystyle }& {\displaystyle }{C}_{\mathrm{T}}={\displaystyle \frac{\mathrm{8}\left(R_{\exp }^{\mathrm{2}}-\mathrm{3}{R}_{\exp }+\mathrm{2}\right)}{{\left(\mathrm{3}{R}_{\exp }-\mathrm{4}\right)}^{\mathrm{2}}}}.\end{array}$$

This unique solution is a maximum, which is apparent from the always-positive value of ΔP in Fig. 4. This figure shows the optimal solution for C_T and C_P, as well as the relative change in radius (ΔR) and power (ΔP) compared to the baseline rotor. In the plots in Fig. 4a and c, C_P is observed to approach the dashed baseline performance (Betz rotor) much faster than C_T as R_exp increases. This is a consequence of the relationship between C_T and C_P (Fig. 1). Especially around the Betz limit, the gradient is very small, which means that changes in C_T do not lead to proportional changes in C_P. Turning to the two plots in Fig. 4b and d, it is seen that the lower C_P is more than compensated for by increasing R since the relative change in power (ΔP) is always positive.

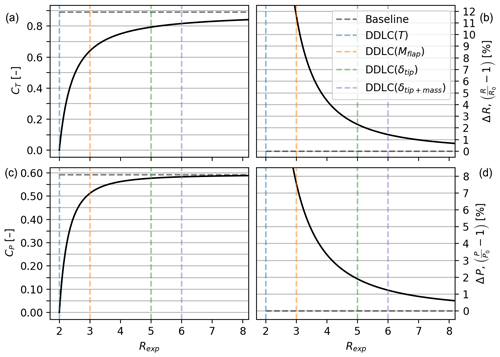
Figure 4 (a) Optimal C_T as a function of the constraint R exponent (R_exp). (c) R_exp vs. C_P; notice that the optimal C_P curve has a steeper slope and hugs the baseline closer than C_T. (b) R_exp vs. relative change in radius ΔR. (d) R_exp vs. relative change in power capture ($\mathrm{\Delta }\stackrel{\mathrm{̃}}{P}$). Despite the similar shape of the curves, a difference between the two is that $\mathrm{\Delta }P(R_{\exp }\to \mathrm{2})=\mathrm{50}$ %, while $\mathrm{\Delta }R(R_{\exp }\to \mathrm{2})\to \mathrm{\infty }$. The vertical lines represent each of the example constraints (^* DDLC: design-driving load constraint).

When maximizing power capture for a given thrust (R_exp=2; dashed vertical blue line in Fig. 4), it is found that C_T→0 and ΔR→∞ while ΔP→50 %, which was found by investigating the behavior of the limit value when R_exp→2. Since ΔR→∞ is not of much practical interest, further explanation is not given here. Alternatively, the maximum power for a given flap root moment (R_exp=3; orange line in Fig. 4) may be achieved by increasing the rotor radius by 11.6 % compared to the baseline design (maximum C_P). The corresponding relative increase in power ΔP is 7.6 %. Finally, designs constrained by tip deflection (R_exp=5; green line in Fig. 4) allow the relative power ΔP to increase by 1.90 % with a relative change in radius ΔR of 2.30 %. A table with the results for the increase in power capture (ΔP) and radius (ΔR) for four designs (R_exp=2, 3, 5, 6) can be seen in Fig. 6. In conclusion, rotors with a static aerodynamic DDLC should not be designed for the maximum C_P, as more power can be generated by rotors with a lower C_T and a larger radius R, without violating the relevant DDLC.

Effect on loads

Even though meeting the constraint limits means that the chosen DDL will be the same as the baseline, it is interesting to know what happens to loads that scale differently than the DDL. As an example, if the DDLC is M_flap (R_exp=3) it is a given that it will not change relative to the baseline, but it could be interesting to know what happens to T and δ_tip.

To investigate it we will introduce a generalized load (L) as a measure of how a load scale.

$$\begin{array}{}\text{(39)}& L=K_{\mathrm{0}}{V}_{\mathrm{0}}^{\mathrm{2}}{C}_{\mathrm{T}}{R}^{L_{\exp }},\end{array}$$

where K₀ is a scaling constant and L_exp is the generalized load exponent. The generalized load equation can be made non-dimensional with

$$\begin{array}{}\text{(40)}& \stackrel{\mathrm{̃}}{L}={\displaystyle \frac{L}{K_{\mathrm{0}}{V}_{\mathrm{0}}^{\mathrm{2}}{R}_{\mathrm{0}}^{L_{\exp }}}}=C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{L_{\exp }}.\end{array}$$

The difference between L_exp and R_exp is that R_exp results in a design, whereas L_exp is a load for a design. Take a design made for tip deflection (R_exp=5) as an example, then L_exp=3 will describe the M_flap load for that design.

An equation for the relative change $\mathrm{\Delta }\stackrel{\mathrm{̃}}{L}$ can be found in terms of the baseline rotor as follows:

$$\begin{array}{}\text{(41)}& \begin{array}{rl}& \left.\begin{array}{l}\stackrel{\mathrm{̃}}{L}=C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{L_{\exp }}\left(\mathrm{40}\right)\\ \stackrel{\mathrm{̃}}{R}={\left(\frac{C_{\mathrm{T},\mathrm{0}}}{C_{\mathrm{T}}}\right)}^{\frac{\mathrm{1}}{R_{\exp }}}\left(\mathrm{30}\right)\\ {\stackrel{\mathrm{̃}}{L}}_{\mathrm{0}}=C_{\mathrm{T},\mathrm{0}}{\stackrel{\mathrm{̃}}{R}}_{\mathrm{0}}^{L_{\exp }}=C_{\mathrm{T},\mathrm{0}}\end{array}\right\}\\ & \Rightarrow \mathrm{\Delta }\stackrel{\mathrm{̃}}{L}={\displaystyle \frac{\stackrel{\mathrm{̃}}{L}}{{\stackrel{\mathrm{̃}}{L}}_{\mathrm{0}}}}-\mathrm{1}={\left({\displaystyle \frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}}\right)}^{\mathrm{1}-\frac{L_{\exp }}{R_{\exp }}}-\mathrm{1}.\end{array}\end{array}$$

Since it is known that $C_{\mathrm{T}}\le C_{\mathrm{T},\mathrm{0}}$ these conclusions follow:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{L}_{\exp }<R_{\exp }\mathrm{The}\mathrm{load}\mathrm{is}\mathrm{lower}\mathrm{than}\mathrm{the}\mathrm{baseline}\mathrm{level}.\\ {\displaystyle }& {\displaystyle }{L}_{\exp }=R_{\exp }\mathrm{The}\mathrm{load}\mathrm{is}\mathrm{identical}\mathrm{to}\mathrm{the}\mathrm{baseline}\mathrm{level}.\\ {\displaystyle }& {\displaystyle }{L}_{\exp }>R_{\exp }\mathrm{The}\mathrm{load}\mathrm{is}\mathrm{larger}\mathrm{than}\mathrm{the}\mathrm{baseline}\mathrm{level}.\end{array}$$

This agrees with Fig. 5, which illustrates the effect of design constraints (DDLCs) on different loads. For example, consider tip deflection (R_exp=5; DDLC(δ_tip); the dashed green line in Fig. 5). Looking at the solid green line (L_exp=5) it is seen that the relative change in L is zero as expected. Now looking at the loads with L_exp<R_exp, namely thrust (L_exp=2) and flap moment (L_exp=3), it is seen that ΔL is lower than the baseline, with $\mathrm{\Delta }T=-\mathrm{6.6}$ % and $\mathrm{\Delta }{M}_{\mathrm{flap}}=-\mathrm{4.4}$ %. But for loads where L_exp>R_exp the loads are increased. If there was a load that scaled like L_exp=6 the load would be increased by $\mathrm{\Delta }{L}_{(L_{\exp }=\mathrm{6})}=+\mathrm{2.3}$ %. Furthermore, Fig. 5 shows that the relative decrease in load is always most pronounced for the thrust (L_exp=2), with the biggest impact occurring around R_exp≈2.5. All of the relative change curves have distinct minima but at the same time are characterized by large plateaus of relatively small change. Another observation is how quickly the curves grow for L_exp>R_exp. Take DDLC(M_flap) as an example; in this case $\mathrm{\Delta }{\mathit{\delta }}_{\mathrm{tip}}=+\mathrm{24.5}$ % and $\mathrm{\Delta }{L}_{(L_{\exp }=\mathrm{6})}=+\mathrm{38.9}$ %. The relative change in loads becomes smaller as R_exp increases. A sketch with a zoomed-in view of the tip and a table with the values can be seen in Fig. 6.

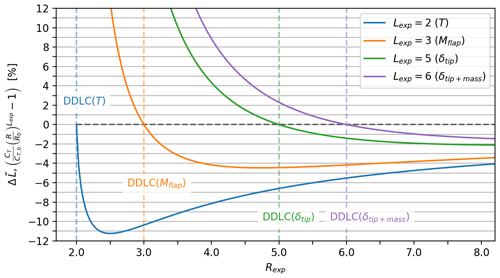
Figure 5 Relative change in different rotor load parameters ($\mathrm{\Delta }\stackrel{\mathrm{̃}}{L}$) depending on DDLC. The scaling of loads have the form $\stackrel{\mathrm{̃}}{L}=C_{\mathrm{T}}{R}^{L_{\exp }}$; e.g., L_exp=2 scales as the rotor thrust T and L_exp=5 scales as the tip deflection δ_tip. Each curve depicts how a load parameter would change depending on the design-driving constraint. As an example, consider a design limited by tip deflection DDLC(δ_tip), i.e., R_exp=5, which matches the dashed green line. Tip deflection meets the requirements, while thrust (T) is lowered by 6.6 % and flap moment M_flap by 4.4 %.

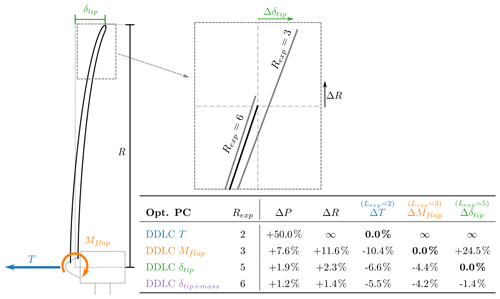
Figure 6 Sketch of a turbine with the load/structural response outlined. The zoomed-in figure shows the radius increase (ΔR) and the change in tip deflection (Δδ_tip) for two different DDLCs (bold black line is the baseline). The table shows the relative change in power, radius and load/structural response for different DDLCs. R_exp=2 is a thrust constraint design, R_exp=3 is a flap moment constraint design, R_exp=5 is a tip-deflection constraint design and R_exp=6 is the tip deflection+constant mass constraint design.

4.2 Low-induction rotor

The concept in this section was mentioned in the Introduction since it has had some attention over the recent years. The low-induction rotors (LIR) are rotors designed with a lower axial induction a than the level that maximizes C_P. The concept is, to a certain degree, analogous with optimization of rotors for power capture.

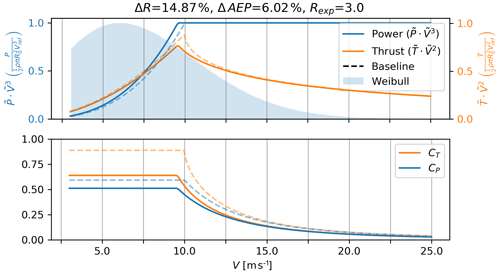
Figure 7 Power and thrust curves for a low-induction rotor (solid lines), designed using the present method with the DDLC exponent R_exp=3, which corresponds to an M_flap constraint. The dashed line is the baseline rotor optimized for a max C_P.

To investigate such an LIR design, it was chosen to fix the C_T value below the rated power in order for it to be the same as for the power-capture optimization for a given R_exp. If the radius was set to the same value as for power capture, it will result in the constraint limit not being met since the turbine reaches the rated power earlier. Since C_T is fixed and the constraint limit needs to be met, the wind speed at which the turbine reaches the rated power (${\stackrel{\mathrm{̃}}{V}}_{\mathrm{rated}}$) can be found. It is found through the normalized power (the integrant of Eq. 7 without the PDF_wind) and the constraint limit with wind speed scaling (Eq. 30 multiplied with ${\stackrel{\mathrm{̃}}{V}}^{\mathrm{2}}$) as follows:

$$\begin{array}{}\text{(42)}& \begin{array}{rl}& \left.\begin{array}{l}\frac{\mathrm{27}}{\mathrm{16}}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}}{\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}=\mathrm{1}\\ \\ {\stackrel{\mathrm{̃}}{V}}^{\mathrm{2}}\frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}{\stackrel{\mathrm{̃}}{R}}^{R_{\exp }}=\mathrm{1}\end{array}\right\}\Rightarrow \\ & {\stackrel{\mathrm{̃}}{V}}_{\mathrm{rated}}={\left({\displaystyle \frac{\mathrm{16}}{\mathrm{27}}}{\displaystyle \frac{\mathrm{2}}{\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}}}{\left({\displaystyle \frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}}\right)}^{\frac{\mathrm{2}}{R_{\exp }}}\right)}^{\frac{\mathrm{1}}{\mathrm{3}-\frac{\mathrm{4}}{R_{\exp }}}}.\end{array}\end{array}$$

For a given rated wind speed the rotor radius can be found using the following steps:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{1}.C_{\mathrm{T}}={\displaystyle \frac{\mathrm{8}\left(R_{\exp }^{\mathrm{2}}-\mathrm{3}{R}_{\exp }+\mathrm{2}\right)}{{\left(\mathrm{3}{R}_{\exp }-\mathrm{4}\right)}^{\mathrm{2}}}}\left(\mathrm{38}\right)\\ {\displaystyle }& {\displaystyle }\mathrm{2}.{\stackrel{\mathrm{̃}}{V}}_{\mathrm{rated}}={\left({\displaystyle \frac{\mathrm{16}}{\mathrm{27}}}{\displaystyle \frac{\mathrm{2}}{\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}}}{\left({\displaystyle \frac{C_{\mathrm{T}}}{C_{\mathrm{T},\mathrm{0}}}}\right)}^{\frac{\mathrm{2}}{R_{\exp }}}\right)}^{\frac{\mathrm{1}}{\mathrm{3}-\frac{\mathrm{4}}{R_{\exp }}}}\left(\mathrm{42}\right)\end{array}$$

$$\begin{array}{}\text{(43)}& \mathrm{3}.\stackrel{\mathrm{̃}}{R}={\left({\displaystyle \frac{\mathrm{1}}{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{rated}}^{\mathrm{2}}}}{\displaystyle \frac{C_{\mathrm{T},\mathrm{0}}}{C_{\mathrm{T}}}}\right)}^{\frac{\mathrm{1}}{R_{\exp }}},\end{array}$$

With C_T, ${\stackrel{\mathrm{̃}}{V}}_{\mathrm{rated}}$ and $\stackrel{\mathrm{̃}}{R}$, $\stackrel{\mathrm{̃}}{\mathrm{AEP}}$ can be computed using Eq. (7).

The LIR is illustrated by the examples in Figs. 7 and 8 where the present analysis framework has been applied with constraints pertaining to flap moments (R_exp=3) and tip deflections (R_exp=5).

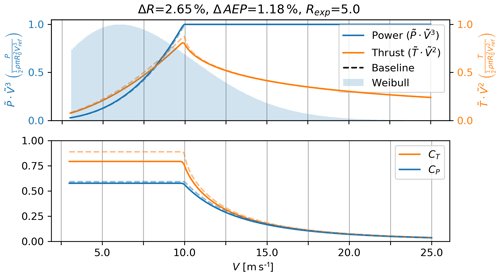
Figure 8 Power and thrust curves for rotor with the DDLC exponent R_exp=5 (solid lines), corresponding to a δ_tip constraint. The dashed line is the baseline rotor optimized for max C_P.

In both cases, the resulting power curves are slightly above the equivalent baseline ones, and the thrust peaks are reduced compared to the baseline. The relative change in AEP results in a smaller change than the change in power at the design point. For the case with DDLC(M_flap), ΔAEP=6.0 % while the power capture increased by ΔP=7.6 %. The corresponding improvements for a tip-deflection-constrained rotor, DDLC(δ_tip), are ΔAEP=1.2 % and ΔP=1.9 %. The lower relative improvement for the LIR is related to the amount of the power that is produced below the rated power. The results for the LIR are summarized in Fig. 9 with a table and a sketch showing the relative changes in AEP, radius, thrust, root-flap moment and tip deflection for four different designs (R_exp=2, 3, 5, 6). From Fig. 9 the thrust constraint design (DDLC(T); R_exp=2) is seen to have diverging values for ΔR, ΔM_flap and Δδ_tip. As was the case for power-capture optimization these results are found from investigating the result of the limit in which R_exp→2. Even though the result of ΔR→∞ is interesting, the corresponding consequence of ΔM_flap→∞ makes this infeasible for practical use, so this will not be studied further here.

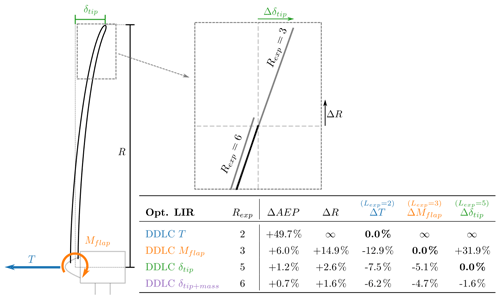
Figure 9 Sketch of a turbine with the load/structural response outlined. The zoomed-in figure shows the radius increase (ΔR) and the change in tip deflection (Δδ_tip) for two different DDLCs (bold black line is the baseline). The table shows the relative change in power, radius and load/structural response for different DDLCs. R_exp=2 is a thrust constraint design, R_exp=3 is a flap moment constraint design, R_exp=5 is a tip-deflection constraint design and R_exp=6 is the tip deflection+constant mass constraint design.

4.3 AEP-optimized rotor

As mentioned in Sect. 3, the variables considered for optimization of AEP are $C_{\mathrm{T}}\left(\stackrel{\mathrm{̃}}{V}\right)$ and $\stackrel{\mathrm{̃}}{R}$. In this formulation, C_T can be adjusted independently for each wind speed, which ideally can be achieved through blade pitch control. The relative radius $\stackrel{\mathrm{̃}}{R}$ couples the rotor operation across all wind speeds, as it is necessarily constant. Based on initial studies, the optimizer targets solutions with three distinct operational ranges, which, ordered by wind speed, are as follows:

• operation with maximum power coefficient (max C_P);

• operation at constraint limit (constant thrust T); and

• operation at the rated power.

This can be used to make C_T a function of $\stackrel{\mathrm{̃}}{R}$, thereby decreasing the optimization problem to an unconstrained optimization in one variable ($\stackrel{\mathrm{̃}}{R}$). The C_T function is given as

$$\begin{array}{}\text{(44)}& \begin{array}{rl}& C_{\mathrm{T}}(\stackrel{\mathrm{̃}}{V},\stackrel{\mathrm{̃}}{R})=\\ & \left\{\begin{array}{lll}\frac{\mathrm{8}}{\mathrm{9}}& \frac{\mathrm{8}}{\mathrm{9}}\le {\stackrel{\mathrm{̃}}{V}}^{-\mathrm{2}}{C}_{\mathrm{T},\mathrm{0}}{\stackrel{\mathrm{̃}}{R}}^{-R_{\exp }}& \left(\max C_{\mathrm{P}}\right)\\ & & \\ {\stackrel{\mathrm{̃}}{V}}^{-\mathrm{2}}{C}_{\mathrm{T},\mathrm{0}}{\stackrel{\mathrm{̃}}{R}}^{-R_{\exp }}& \mathrm{1}\le \frac{\mathrm{27}}{\mathrm{16}}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}}{\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}& \left(\mathrm{constraint}\mathrm{limit}\right)\\ & & \\ \mathrm{1}=\frac{\mathrm{27}}{\mathrm{16}}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}}{\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}& \mathrm{1}>\frac{\mathrm{27}}{\mathrm{16}}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}-C_{\mathrm{T}}}\right)C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{R}}^{\mathrm{2}}{\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}& \left(\mathrm{rated}\mathrm{power}\right),\end{array}\right.\end{array}\end{array}$$

where the last equation needs to be solved to get C_T; the solution is a third-order polynomial, which is more easily solved numerically.

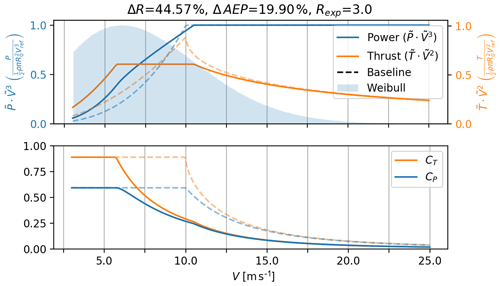
Figure 10 Power and thrust curve for an AEP-optimized rotor (solid lines) where the DDLC exponent is R_exp=3, which is equivalent to a constraint on M_flap. The dashed line is the baseline rotor optimized for the max C_P below the rated power.

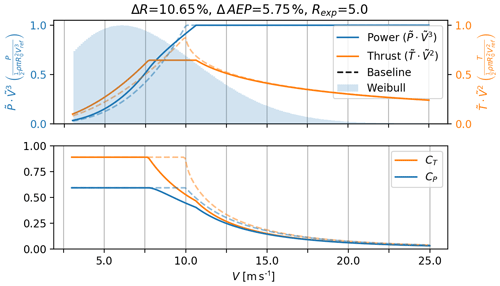
Figure 11 Power and thrust curve for an AEP-optimized rotor (solid lines) where the DDLC exponent is R_exp=5, which is equivalent to a constraint on δ_tip. The dashed line is the baseline rotor optimized for the max C_P below the rated power.

The only free parameter that needs to be determined to find the optimal AEP is $\stackrel{\mathrm{̃}}{R}$. The optimization problem can be reformulated as

$$\begin{array}{}\text{(45)}& \underset{\stackrel{\mathrm{̃}}{R}}{\mathrm{maximize}}\stackrel{\mathrm{̃}}{\mathrm{AEP}}=\underset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CI}}}{\overset{{\stackrel{\mathrm{̃}}{V}}_{\mathrm{CO}}}{\int }}\stackrel{\mathrm{̃}}{P}\left(C_{\mathrm{T}}(\stackrel{\mathrm{̃}}{V},\stackrel{\mathrm{̃}}{R}),\stackrel{\mathrm{̃}}{R}\right)\cdot {\stackrel{\mathrm{̃}}{V}}^{\mathrm{3}}\cdot {\mathrm{PDF}}_{\mathrm{wind}}\left(\stackrel{\mathrm{̃}}{V}\right)\mathrm{d}\stackrel{\mathrm{̃}}{V}.\end{array}$$

The problem can be solved with most optimization solvers since the AEP can be computed explicitly if $\stackrel{\mathrm{̃}}{R}$ is given. The optimization problem was solved with the L-BFGS-B algorithm described in Zhu et al. (1997) though the use of SciPy (Millman and Aivazis, 2011).

Examples of the resultant power and thrust curves can be seen in Figs. 10 and 11, for DDLC(M_flap) and DDLC(δ_tip), respectively. Looking at Fig. 10 (R_exp=3) it is clear that the power and thrust curves have changed quite substantially, compared to the baseline Betz rotor (dashed curves). The thrust curve does not have a sharp peak anymore but rather a flat plateau. As mentioned in the Introduction this is often referred to as thrust clipping. It comes from the DDLC equation (Eq. 44) which shows that $C_{\mathrm{T}}\propto {\stackrel{\mathrm{̃}}{V}}^{-\mathrm{2}}$, and since thrust is proportional to $T\propto C_{\mathrm{T}}{\stackrel{\mathrm{̃}}{V}}^{\mathrm{2}}$, it means that the thrust is constant. As mentioned, the region where the rotor is thrust clipped is also where the DDLC is active, so opposed to the baseline and LIR rotor, the DDLC is active over a larger range of V. The larger range of V is also partly why ΔR=44.6 %, which is a huge increase. As a result, it also leads to a large increase, with ΔAEP=19.9 %. This is a very large change in $\stackrel{\mathrm{̃}}{R}$ and the feasibility of such a design is doubtful. As it is shown later, the change in maximum loads (see Fig. 13) leads to a significant change in loads with L_exp>R_exp.

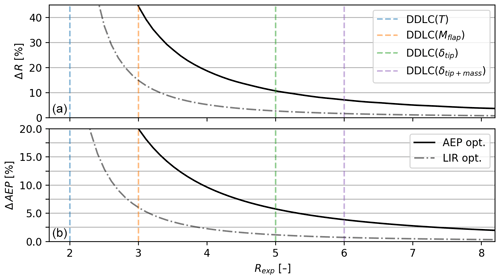
Figure 12 DDLC exponent (R_exp) vs. (a) relative change in radius (ΔR) and (b) relative change in AEP ($\mathrm{\Delta }\stackrel{\mathrm{̃}}{\mathrm{AEP}}$). The plot contains both of the changes for the cases of the low-induction rotor (LIR opt.; dashed–dotted black line) and the AEP-optimized rotor (AEP opt.; black solid). The changes in both AEP and radius are much larger for the AEP-optimized rotor.

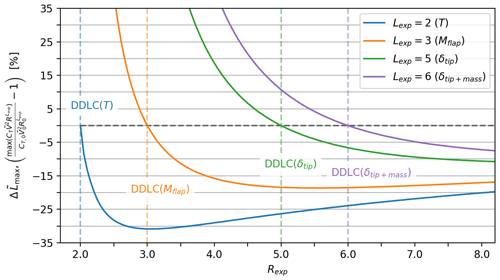
Figure 13 DDLC R exponent (R_exp) vs. relative maximum load ($\mathrm{\Delta }{\stackrel{\mathrm{̃}}{L}}_{\max }$). The plot looks similar to Fig. 5 but $\mathrm{\Delta }{\stackrel{\mathrm{̃}}{L}}_{\max }$ is the change in maximum loading. As an example, when thrust (T) is −30.8 % for R_exp=3 it means that the maximum thrust (for any wind speed) is 30.8 % lower than the maximum thrust for the baseline (which happens just before the rated wind speed). Notice that the range for the y scale is much larger in this plot than for the power-capture-optimized rotor. The potential reduction is more, but it comes with the consequence that L_exp>R_exp grows faster even for high values of R_exp.

A more realistic design for modern turbines is found in Fig. 11 (R_exp=5). Here the changes are fewer but still significant with ΔR=10.7 % and ΔAEP=5.8 %. It shows the same shape as the thrust-clipped curve, but now it is over a smaller range of V. As mentioned in the Introduction, thrust clipping was also found by Buck and Garvey (2015a) to be a beneficial way to lower CoE.

In Fig. 12 the relative change in R and AEP can be seen as a function of the DDLC R exponent. The plot both contains the result for the AEP-optimized rotor (AEP opt.; solid black line) and the low-induction rotor (LIR opt.; dashed–dotted gray line). The difference between the two is significant, especially for ΔAEP. The results for the AEP-optimized rotor are summarized in Fig. 14 with a table and a sketch that shows the relative changes. As was the case for power-capture optimization and LIR optimization, some values diverge when R_exp→2, and the results are found by investigating this limit. But since it has no practical value, further explanation is omitted here.

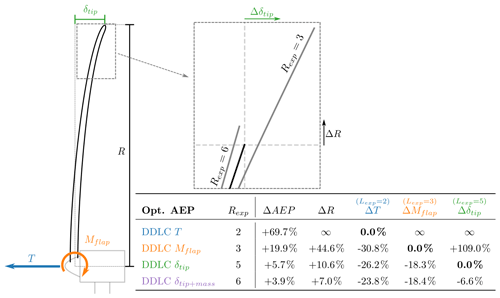
Figure 14 Sketch of a turbine with the load/structural response outlined. The zoomed-in figure shows the radius increase (ΔR) and the change in tip deflection (Δδ_tip) for two different DDLCs (bold black line is the baseline). The table shows the relative change in power, radius and load/structural response for different DDLCs. R_exp=2 is a thrust constraint design, R_exp=3 is a flap moment constraint design, R_exp=5 is a tip deflection constraint design and R_exp=6 is tip deflection+constant mass constraint design.

Effect on loads

In Fig. 13 a plot of the relative change in maximum loads as a function of the DDLC R exponent. The relative max load ($\mathrm{\Delta }{\stackrel{\mathrm{̃}}{L}}_{\max }$) does not compare the loads at each $\stackrel{\mathrm{̃}}{V}$ but rather the max load for the baseline at $\stackrel{\mathrm{̃}}{V}=\mathrm{1}$ (rated wind speed) to the max load for the optimized rotor for any $\stackrel{\mathrm{̃}}{V}$. The plot in Fig. 13 is similar to the plot in Fig. 5 with the difference being that it is the relative change in maximum loads, independent of wind speed at which it occurred. Comparing the two plots, one should note the range for the y scale in the two plots, with Fig. 13 having the larger range. It also means that the relative change in the loads for the AEP-optimized rotor experiences a larger relative change. But it also has the consequence that loads with L_exp>R_exp grow faster, especially for larger values of R_exp (>5). A summary of the AEP-optimized rotor can be seen in Fig. 14, where a table of four different designs (R_exp=2, 3, 5, 6) shows the relative change in AEP, radius, thrust, root-flap moment and tip deflection.

4.4 Summary of findings

In Table 1 the tables shown in Figs. 6, 9 and 14 are summarized. It compares the different optimizations to each other.

Table 1 Overview of the optimization results from optimizing power capture (Opt. PC), low-induction rotor (Opt. LIR) and annual energy production (Opt. AEP).

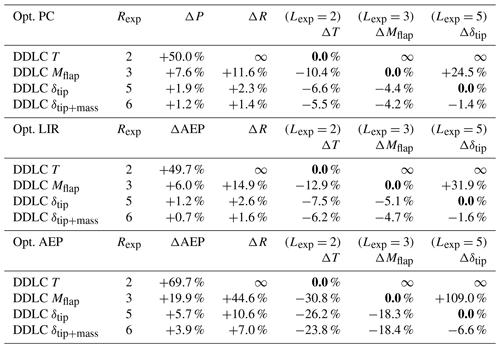
As seen from the tables, the largest increase in ΔP∕AEP is found using AEP optimization, which also leads to the largest increase in rotor radius (ΔR). It also shows that using thrust clipping seems to be a better operational strategy than low induction, as the design-driving constraint can be met over a larger range of wind speeds and low induction is only needed around maximum thrust and not at low wind speeds.

In all three optimization cases, the optimization of the design with thrust constraint (DDLC(T); R_exp=2) leads to divergent values for ΔR and the loads. In all cases the result is found by investigating the behavior of the limit when R_exp→2. Since this is not thought to be of much practical value, the details are not provided here.

4.5 Limitation of the study and possible improvements

The study shows that for a rotor constraint by a static aerodynamic DDL there is a benefit to lowering the loading and increasing the rotor size in terms of power/AEP. But, as it was found by Bottasso et al. (2015), having a rotor with the same load constraint and increasing the radius does not mean that the cost is the same or that it is cost optimal. They found that the increase in AEP did not compensate for the added cost from increasing the rotor radius. This problem of cost vs. benefit is not directly addressed in this paper, but by the DDLC δ_tip+mass, a constraint in which the mass is kept constant. It is thought to be a better approximation for a rotor with a fixed price – but this assumption needs to be tested.

Another issue that is not taken into account in this study is the influence of the turbines self-weight. As was found by Sieros et al. (2012) the self-weight becomes more important for larger rotors. To accommodate for the added mass, a penalty could be added which should scale as $\stackrel{\mathrm{̃}}{R}$ or ${\stackrel{\mathrm{̃}}{R}}^{\mathrm{3}}$ for top head mass and static blade mass moment, respectively. As discussed above, there could also be a constraint implemented that will keep the mass or the mass moment in the optimization. Again this is a limitation of the study.

The fidelity of the models is also a limitation. Even though 1-D aerodynamic momentum theory is a common approximation to do for first-order studies in rotor design, it is well known that the constantly loaded rotor is not possible to realize, and when losses are included the constantly loaded rotor is not the optimal solution anymore. At the same time, if it was possible to decrease the load at the tip more than at the root, it would lead to less tip deflection than a constantly loaded rotor with a similar C_T. Extending the model to be able to handle radial load distribution is one way of adding detail to the model that could lead to even larger improvements. It could be done through the use of blade element momentum (BEM) theory.

For modern turbine design, it is often the case that the structural design is determined by the aeroelastic extreme loads, such as extreme turbulence or gusts. With the simplicity of the models in this study, this is not taken into consideration. But if the extreme load happens in normal operation there will likely be a direct relationship between the steady and extreme loads, meaning that a decrease in steady loads will also lead to a decrease in the extreme load. This is an assumption that should be tested in future work. If the design-driving load is happening in nonoperational conditions, e.g., extreme wind in parked conditions, grid loss or subcomponent failure, then the analysis tool cannot be directly applied.

5 Conclusions

A first-order model framework for the analysis of wind turbine rotors was developed based on aerodynamic 1-D momentum theory and Euler–Bernoulli beam theory. This framework introduces the concept of design-driving load (DDL) for which a generalized form has been developed in which loads only differ by a scaling exponent R_exp, e.g., thrust scales as R_exp=2, root-flap moment as R_exp=3 and tip deflection as R_exp=5. Despite the simplicity of the model, this study has shown important trends in how to design rotors for maximum power capture. It has been shown that the potential increase in power capture is very dependent on the relevant constraint, e.g., thrust as the constraining load compared to the more restrictive tip deflection. Furthermore, it was concluded that the best way to design a rotor for increased power capture using aeroelastic considerations is not to maximize C_P but rather to relax C_P and operate at lower loading (lower C_T). How much one should relax C_P depends on the chosen design-driving constraint (R_exp). The results for optimizing for power capture are summarized in Table 1 (Opt. PC).

The optimization of power capture determines the best possible design for a given wind speed. By considering the annual energy production (AEP), an optimal design across the range of operational wind speeds can be found for a given wind speed frequency distribution. Optimal AEP was considered with two different approaches, namely the low-induction rotor (LIR) and full AEP optimization. For LIR, the C_T value below the rated power was set to the value found from power-capture optimization for the chosen R_exp. Then the radius was increased compared to the power-capture-optimized rotor, since it will reach the rated power earlier with the same rotor size. A summary of the results can be seen in Table 1 (Opt. LIR).

For the full AEP optimization, C_T was allowed to take on any positive value below the Betz limit ($\mathrm{0}\le C_{\mathrm{T}}\le \mathrm{8}/\mathrm{9}$) for all wind speeds. The optimal AEP is obtained for a rotor that operates in three distinct operational regimes:

• operation with maximum power coefficient (max C_P);

• operation at constraint limit (constant thrust T); and

• operation at the rated power.

The results from the optimization are summarized in Table 1 (Opt. AEP). It shows significantly larger relative improvements in power/energy compared to power-capture- and LIR-optimized rotors. This comes at the cost of a larger increase in rotor radius. In the range where the optimum turbine operates at the constraint limit, the thrust curve is clipped (in a manner also known as peak shaving or force capping). This is a control feature used for many contemporary turbines, so it is interesting that this study, independent of this knowledge, shows that thrust clipping is a very efficient way to increase energy capture while observing certain load constraints. It is also the main reason behind the relatively large possible improvements in AEP, as the constraint limit is met over a larger range of wind speeds.

In spite of relatively crude model assumptions made, this paper provides profound insight into the trends of rotor design for maximum power/energy, e.g., the use of thrust clipping. As wind turbine rotors continue to develop towards larger diameters with slender (more flexible) blades, the type of design-driving load constraint also evolves. With the present model framework, the conceptual implications of this development become clearer; an increase in AEP of up to 5.7 % is possible compared to a traditional C_P-optimized rotor – without changing technology, using bend-twist coupling or other advanced features. Finally, this work has demonstrated an approach to formulate an optimization objective that couples power and load/structural response though the power-capture optimization. This approach may be extended into less crude model frameworks, e.g., by introducing radial variations in rotor loading.