the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Brief communication: A double-Gaussian wake model
Johannes Schreiber
Amr Balbaa
In this paper, an analytical wake model with a double-Gaussian velocity distribution is presented, improving on a similar formulation by Keane et al. (2016). The choice of a double-Gaussian shape function is motivated by the behavior of the near-wake region that is observed in numerical simulations and experimental measurements. The method is based on the conservation of momentum principle, while stream-tube theory is used to determine the wake expansion at the tube outlet. The model is calibrated and validated using large eddy simulations replicating scaled wind turbine experiments. Results show that the tuned double-Gaussian model is superior to a single-Gaussian formulation in the near-wake region.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(1935 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(1935 KB) - Full-text XML
- Corrigendum
- BibTeX
- EndNote
Analytical engineering wind farm models are low-fidelity approximations used to simulate the performance of wind power systems. A wind farm model includes both a model of the wind turbines and a model of the modifications to the ambient flow induced by their wakes, together with their mutual interactions. Analytical wake models, as opposed to high-fidelity computational fluid dynamics (CFD) models, are simple, easy to implement, and computationally inexpensive. In fact, they only simulate macroscopic average effects of wakes and not their small scales or turbulent fluctuations. Engineering wake models find applicability in all those cases that do not need to resolve small spatial and fast temporal scales, such as the calculation of the power production of a wind plant over a sufficiently long time horizon. Such models are also extremely useful in optimization problems, where a large number of simulations might be required before a solution is reached or where calculations need to be performed on the fly in real time. Analytical wake models are thus often utilized in wind farm layout planning and in the emerging field of wind farm and wake control (Scholbrock, 2011; Churchfield, 2013; Boersma et al., 2017).
Because of their indisputable usefulness, engineering wake models have been extensively studied in the literature. The Jensen (PARK) formulation is one of the most widely used wake models, to the extent that it is sometimes considered the industry standard (Keane et al., 2016). The model was first introduced by Jensen (1983) and later further developed by Katić et al. (1986). Other widely used and cited wake models include the Frandsen model (Frandsen et al., 2006), the FLORIS model (Gebraad et al., 2014), and the EPFL Gaussian models (Bastankhah and Porté-Agel, 2014, 2016).
All such models have been designed to faithfully represent the average flow properties of the far-wake region. However, in the near wake (which is usually defined as the region up to about 4 diameters (4 D) downstream of the rotor disk), the models seem to lack accuracy. Nowadays, onshore wind farms tend to be closely packed, and turbine spacing often reaches values close to or even below 3 D (Schreiber et al., 2018; energiespektrum.de, 2015). This raises the necessity of developing models that accurately represent the wake not only far away from the rotor disk but also in the near and mid-wake regions.
Keane et al. (2016) developed a wake model featuring a double-Gaussian velocity deficit distribution in an attempt to formulate a model that closely resembles observed speed distributions in both the near- and far-wake regions. In fact, while a single-Gaussian function is considered to be a good approximation of the wake velocity distribution in the far wake (Bastankhah and Porté-Agel, 2014, 2016), the near wake is better approximated using a double-Gaussian distribution. This is due to the presence of two minima in the speed profiles close to the rotor disk, as also observed in experimental measurements and high-fidelity CFD simulations (Wang et al., 2017). The double-Gaussian model by Keane et al. (2016), which is referred to as the Keane model in this paper, was developed in a similar fashion to the EPFL Gaussian model (Bastankhah and Porté-Agel, 2014), and it was intended to respect the principles of mass and momentum conservation.
In this short note, a double-Gaussian wake model, based on Keane's model and with emphasis on near-wake flow behavior, is derived, calibrated, and validated. The present formulation addresses and resolves some issues found in the original implementation of Keane et al. (2016), primarily concerning momentum conservation. In addition, the wake expansion function is defined such that mass flow deficit conservation is achieved at the stream-tube outlet.
This paper is organized as follows. The derivation of the double-Gaussian wake model is detailed in Sect. 2, along with the formulation of the wake expansion function. In Sect. 3, the model is tuned and validated, using both experimental measurements obtained with scaled models in a boundary layer wind tunnel and by numerical results of high-fidelity large eddy simulations (LESs). Additionally, the performance of the double-Gaussian model is compared to a standard single-Gaussian formulation. Concluding remarks and future work recommendations are given in Sect. 4. Finally, Appendix A derives some integrals appearing in the formulation.
2.1 Double-Gaussian velocity deficit
The double-Gaussian wake model is derived in a similar way to the Frandsen (Frandsen et al., 2006) and EPFL single-Gaussian models (Bastankhah and Porté-Agel, 2014). Following their approach, the conservation of momentum principle is applied on an ansatz velocity deficit distribution, which includes an amplitude function. Thereby, an expression for the amplitude is obtained that assures conservation of momentum.
At the downstream distance x from the wind turbine rotor and at the radial distance r from the wake centerline, the wake velocity deficit is modeled as the product of the normalized double-Gaussian function g(r,σ(x)), which dictates the spatial shape of the deficit, with the amplitude function C(σ(x)). This yields
where U∞ represents the ambient wind speed and U(x,r) the local flow velocity in the wake. The double-Gaussian wake shape function, which is symmetric with respect to the wake center, is defined as
where r0 is the radial position of the Gaussian extrema. The standard deviation of the Gaussian function, noted σ(x), represents the width (cross section) of each of the two single-Gaussian profiles. The wake expands with downstream distance x, causing the transformation of the initial double-Gaussian profile in the near wake, through a flat-peak transition region, into a nearly single-Gaussian profile in the far wake. The wake expansion function is discussed in further detail in Sect. 2.2. A possible improvement to the present model might include an azimuth-dependent double-Gaussian function. This would allow one to model a non-axisymmetric double-peaked wake profile, caused by a sheared inflow and/or by the misalignment of the rotor axis with respect to the wind, at the cost of extra tuning parameters.
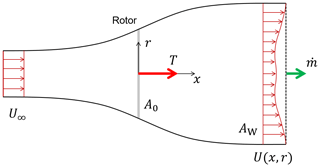
Figure 1Stream tube with nomenclature: U∞ is the ambient wind speed; U(x,r) is the local flow velocity in the wake at the downstream position x and radial distance r from the wake centerline; is the mass flow rate through the stream tube; AW is a planar cross-sectional area large enough to contain the wake deficit; A0 is the rotor disk area; and T is the thrust force (by the principle of action and reaction, an equal and opposite force is applied by the rotor onto the flow).
The conservation of momentum principle is now applied on the ansatz velocity deficit distribution, using the amplitude function C(σ(x)) as a degree of freedom. Accordingly, the axial thrust force T is related to the rate of change of momentum p of the flow throughout the stream tube (see Fig. 1), i.e.,
where is the mass flow rate through the stream tube, an effective wake velocity deficit, ρ the air density, and AW a planar cross section at least large enough to contain the wake deficit. Equation (3) is only valid if there is an equal pressure and negligible flow acceleration at the inlet and outlet sections of the stream tube and, additionally, if shear forces on the control volume can be neglected. The thrust force T is customarily expressed through the nondimensional thrust coefficient CT as
where A0 is the rotor swept area.
If the wake velocity, defined in Eqs. (1) and (2), is substituted into the Eq. (3), one obtains
Note that as the double-Gaussian wake expands all the way to infinity, the integral boundary is set accordingly. The integration of Eq. (5), whose details are provided in Appendix A, yields
where
By substituting the thrust given by Eq. (4) into Eq. (6), and solving the resulting quadratic equation for the amplitude function C(σ), one obtains
where is the rotor diameter. Both solutions of the amplitude function C(σ) would theoretically lead to the conservation of momentum at all downstream distances. However, the velocity profiles obtained by using C+(σ) are characterized by a negative speed (i.e., in the direction opposite to the ambient flow), and thus C+(σ) is deemed to be a nonphysical solution. Therefore, the true solution for the amplitude function is C−(σ). In addition, a momentum-conserving solution exists only if , which might not always be the case for large values of CT.
The derived expressions for M and N presented in this paper differ from the results reported in the original publication by Keane et al. (2016), even though all assumptions are identical. The expressions reported in the original paper were also evaluated numerically, yielding nonphysical results that violate the conservation of mass and momentum underlying the formulation.
2.2 Wake expansion function
In the previous section, following the conservation of momentum, the shape of the double-Gaussian wake deficit has been defined as a function of the Gaussian parameter σ. In this section, a wake expansion function σ(x) is introduced, which is linear with respect to the downstream distance x. By mass conservation, the wake expansion at the position of the stream tube outlet is therefore identified.
In previous work by Frandsen et al. (2006) and Bastankhah and Porté-Agel (2014), stream tube theory was employed to derive an equation for the initial wake width at the turbine rotor. Thereby, the number of tunable parameters of the wake expansion function is reduced, facilitating model calibration. However, this approach includes the assumption that the stream tube outlet is located exactly at the turbine rotor itself, which is hardly true. Results indicate that the derived initial wake width is too large to fit experimental measurements, which in turn requires a model retuning (Bastankhah and Porté-Agel, 2014).
In the present work, the stream tube outlet is not assumed to be located at the turbine rotor (x=0) but at the unknown downstream position x0. Therefore, the expansion function is defined as
where parameter k* controls the rate of expansion, while ϵ represents the wake expansion at x0. The wake expansion function is assumed to be linear as in Bastankhah and Porté-Agel (2014).
To derive ϵ, mass conservation between the Betz stream tube and the wake model is enforced. Starting from Eq. (3), Frandsen et al. (2006) and Bastankhah and Porté-Agel (2014) show that the mass flow deficit rate at the outlet of a Betz stream tube (noted ST) can be written as
where UST is the uniform cross-sectional wake velocity. In this expression, β is the ratio between the stream tube outlet area AST and the rotor disk area A0, which can be expressed as a function of the thrust coefficient CT as
At the Betz stream tube outlet (x=x0), the mass flow deficit rate of the double-Gaussian (noted DG) wake model writes as
By equating both mass flow deficits (i.e., ), the initial wake expansion ϵ can be derived. The solution was computed numerically as a function of the thrust coefficient CT and the spanwise location of the Gaussian extrema r0. The resulting surface is presented in Fig. 2. Note that the solution to stream tube theory is defined only in the range , and ϵ tends to infinity as the thrust coefficient approaches the value of 1, due to mass conservation.
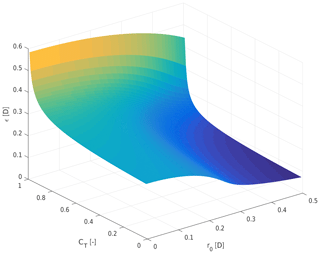
Figure 2Visualization of the width of the double-Gaussian function ϵ at the stream tube outlet, as a function of the thrust coefficient CT and the position of the Gaussian extrema r0.
The remaining parameters, x0 and k*, in the linear wake expansion function expressed by Eq. (9) are not explicitly modeled, and they should be tuned based on experimental measurements or high-fidelity simulations, as shown in the next section. Note that the underlying momentum conservation statement expressed by Eq. (3) has only been defined for ambient pressure. Therefore, the formulation is, strictly speaking, only valid for x≥x0. However, as pressure recovers rapidly immediately downstream of the rotor, reasonable approximations can also be expected for x<x0. Finally, k* is expected to depend on atmospheric conditions (Peña et al., 2016) and turbine thrust (Campagnolo et al., 2019).
3.1 Experimental and simulation setup
To calibrate and validate the double-Gaussian wake
model, time-averaged flow measurements from an LES numerical solution have
been used. The CFD simulation replicates an experiment conducted with the
scaled G1 wind turbine
(Campagnolo et al., 2017, 2019),
which has a 1.1 m rotor diameter and a 0.8 m hub height. Its design operating
tip speed ratio is 8 and its rated rotor speed is 850 rpm. The G1
model is designed such that the characteristics of its wake are realistic in
terms of shape, velocity deficit, and recovery. In addition, the model
features closed-loop pitch, torque and yaw control, and load sensors
located at the shaft and tower base (Campagnolo et al., 2017). The experiment
was conducted with a single G1 wind turbine model in the
boundary layer wind tunnel at Politecnico di Milano. The wake profile was measured using hot-wire probes at the downstream distances from the turbine. At each downstream location, the velocity was measured
at hub height at different lateral positions y and then time averaged to
obtain a steady-state value. The ambient wind velocity within the wind tunnel
was measured using a pitot tube placed upwind of the G1 model. The
wind tunnel experiment was conducted with a 5 m s−1 hub height wind
speed, a power law exponent of 0.144, and a turbulence intensity of approximately 5 %, with the wind turbine operating at CT≈0.75.
A complete digital copy of the experiment was developed with the LES simulation framework developed by Wang et al. (2017), which includes the passive generation of a sheared and turbulent flow, an actuator line model of the wind turbine implemented with the FAST aeroservoelastic simulator (Jonkman and Buhl Jr., 2005) and the tunnel walls. The simulation model includes also a slight lateral nonuniformity of the inflow, in the form of a 2.7 % horizontal shear, caused by the wind tunnel internal layout upstream of the test chamber and by the tunnel fans. The proposed double-Gaussian wake model was calibrated and validated using time-averaged CFD simulation results at the same downstream distances as the experiments, numerical and experimental measurements being in excellent agreement with each other.
3.2 Parameter identification and results
The double-Gaussian model proposed in this work has three tunable parameters: k*, x0, and kr. Parameters k* and x0 are used to describe the wake expansion downstream of the turbine rotor, as expressed by Eq. (9). The third parameter, kr, is defined as , and it describes the position of the Gaussian extrema. When kr=1 the curve extrema are located at the tip of the rotor blades, while for kr=0 the two Gaussian functions coincide at the wake center, leading to a single-Gaussian wake profile.
In the original formulation by Keane, kr was fixed at 75 % blade span, as it was argued that most lift is extracted from the flow at this location. In the present work the parameter is tuned based on measurements, as the assumed 75 % blade-span position did not lead to satisfactory results.
The goal of model calibration is to ensure that the wind velocity profiles
match the reference data set as closely as possible. To this end, the squared
error between the wake model and CFD-computed wake profiles is minimized with
respect to the free parameters. This estimation problem was solved using the
Nelder–Mead simplex algorithm implemented in the MATLAB function
fminsearch (Lagarias et al., 1998). To ensure the generality of the
results, only a subset of the reference data was used for parameter
estimation (namely the downstream distances 1.7, 3, and 6 D), while the
others were used for verification purposes.
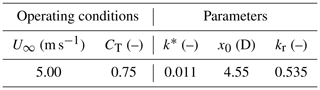
The identified parameters are presented in Table 1. The Gaussian extrema were found to be at approximately 53.5 % of blade span (kr=0.535), while the wake width at x0 is ϵ=0.23 D. Model calibration also resulted in the positioning of the stream tube outlet at x0=4.55 D, which appears to be a realistic value for the investigated turbine.
Figure 3 shows the experimental wake measurements using black circles, for all available downstream distances. The CFD results, shown using red × symbols, are almost identical to the experimental measurements, highlighting the quality of the LES simulations. The predictions of the double-Gaussian model are shown in solid blue lines.
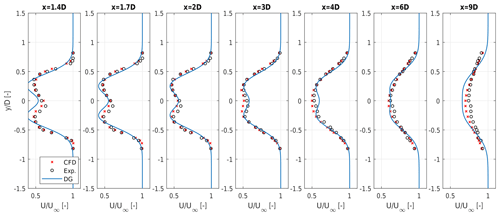
Figure 3Normalized wind velocity profiles of the double-Gaussian model (solid blue line) compared to experimental measurements (black circles) and CFD simulations (red × symbols). The distances 1.7, 3, and 6 D were used for model calibration.
The model exhibits good generality, as demonstrated by the good matching of the profiles at distances that were not used for model estimation. Especially in the near-wake region up to about 3 D, the placement of the Gaussian extrema appears to be in good agreement with the measured one.
The performance of the model clearly depends on the data used for its calibration. Using reference data close to the turbine rotor is important for accurately gauging the positions of the velocity profile extrema, while a wider rage of distances leads to an improved expansion behavior. In the present case, more data from the near-wake region (1.7 and 3 D) were considered in the tuning process than in the far wake (6 D). This leads to a slight overestimation of the velocity deficit at 9 D, which could be attributed to an underestimation of the expansion slope k*. However, tuning the model using the entire set of reference data points leads to only small differences in the identified parameters, which in turn produce wake profiles that are fairly similar to the ones presented here. On the other hand, identifying the model using only data points from the far wake resulted in better fitting results at 9 D but with either very small values of r0 – which led to nearly single-Gaussian profiles – or with high values of the k* expansion slope – which led to nonphysical solutions of Eq. (8) for the amplitude function in the near-wake region, due to excessively small Gaussian widths.
Figure 4 depicts with a solid blue line and * symbols the root mean square error (RMSE) between the DG wake model (based on the parameters reported above, obtained from measurements at 1.7, 3, and 6 D) and the reference CFD data as a function of downstream distance. To identify a lower error bound, the DG wake model parameters were also tuned separately at each downstream distance, obtaining seven different local parameterizations. The corresponding RMSE with respect to the CFD solution is reported in the same figure using a dashed blue line. The small difference between the two curves shows that the single (global) parameterization computed using only three distances is only marginally suboptimal, in the sense that it is very close to the best possible fitting that a double-Gaussian shape function can achieve. The plot shows also a slight increase in the difference between the two curves in the far-wake region, which can again be attributed to the fact that only one large-distance (6 D) measurement was used in the global tuning.
As a comparison, Fig. 4 also shows the results obtained with the EPFL single-Gaussian (SG) model (Bastankhah and Porté-Agel, 2014). The SG model was identified with the same procedure and measurements used for the DG model, obtaining ϵSG=0.3177 and ; the corresponding RMSE with respect to the CFD results is reported in the figure using a solid red line with circles. The lower error bound for the SG model, here again obtained by tuning the parameters independently at each one of the seven available downstream distances, is shown using a dashed red line. As expected, the SG wake model shows a significantly larger RMSE in the near-wake region than in the DG case. In fact, here the wake profile is indeed characterized by two peaks, so that the double-Gaussian shape function allows for a more precise representation of the actual flow characteristics. Here again it should be noted that the difference between the global and local parameterizations is quite small, which strengthens the conclusion that improved results are due to the ansatz velocity deficit distribution and not to the specific parameterizations. Comparing the SG with the DG model, Fig. 4 shows that both reach very similar RMSEs for 9 D. The similarity between the two models continues for larger downstream distances.
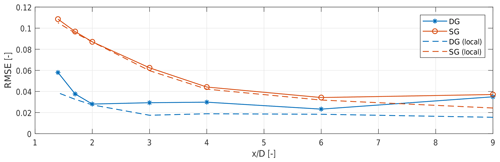
Figure 4Root mean square error between the reference CFD velocity deficit data and the engineering wake models. Double-Gaussian (DG) wake model identified using measurements at 1.7, 3, and 6 D: solid blue line with * symbols. DG wake model parameterized locally at each downstream distance: dashed blue line. Single-Gaussian (SG) EPFL wake model identified using measurements at 1.7, 3, and 6 D: solid red line with circles. SG EPFL wake model parameterized locally at each downstream distance: dashed red line.
This short paper presented an analytical double-Gaussian wake model. The proposed formulation corrects and improves a previously published model proposed by Keane et al. (2016). The shape of the velocity deficit distribution in the wake is described by two Gaussian functions, which are symmetric with respect to the wake center, while the amplitude of the velocity deficit is derived using the principle of momentum conservation. A linear expansion of the width of the Gaussian profiles was assumed, and stream tube theory was used to estimate the conditions at the stream tube outlet.
The model was calibrated and validated using a set of time-averaged CFD simulation results, which replicate wind tunnel experiments performed with a scaled wind turbine in a boundary layer wind tunnel. Results show that the model fits the reference data with good accuracy, especially in the near-wake region where a single-Gaussian wake is unable to describe the typically observed bimodal velocity profiles. In the far wake, a slight overestimation of the wake deficit could be observed. It is speculated that this might be due to the wake expansion gradient being slightly different in the near- and far-wake regions. This claim, however, would need additional work to be substantiated. The different shape of the wake in the near- and far-wake regions also suggests stitching the two models together, the double Gaussian being used in the near-wake region and the single Gaussian further downstream. This would avoid the need for a single tuning that has to cover such a long distance and different behaviors. Additional future work could extend the wake model to include wake deflection, which could be done in a rather straightforward manner by following Bastankhah and Porté-Agel (2016). In this case, a nonsymmetric double-Gaussian shape function could be used to model the kidney shape of a deflected wake (Bartl et al., 2018). More in general, an azimuth-dependent double Gaussian might be used to account for the effects of both misalignment and a sheared inflow.
Equation (5) can be written as
where
In the following, integrals M and N are solved to obtain Eq. (7a) and (7b).
A1 Derivation of M
M can be split into two terms:
Term I1 is defined as
Noting that , one gets
where erf is the Gauss error function,
and its complementary function. Similarly, I2 writes as
and its integral is computed as
Combining the previous results, one gets Eq. (7a), i.e.,
A2 Derivation of N
Term N can be split into three terms
Terms I3 and I4 are collectively defined as
Solving the integral yields
Finally, I5 is defined as
which, once integrated, gives
Therefore, one gets
which corresponds to Eq. (7b).
A MATLAB implementation of the wake model and the data contained in this article can be obtained by contacting the authors.
JS conducted the main research work, AB implemented the correct model and CLB closely supervised the whole research. All three authors provided important input to this research work through discussions, feedback and by writing the paper.
The authors declare that they have no conflict of interest.
The authors express their gratitude to Jesse Wang and Filippo Campagnolo of the Technical University of Munich, who respectively provided the numerical and experimental wake measurements.
This research has been partially supported by the European Commission, H2020 Research Infrastructures (CL-Windcon (grant no. 727477)).
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
This paper was edited by Gerard J. W. van Bussel and reviewed by Matthew J. Churchfield and one anonymous referee.
Bartl, J., Mühle, F., Schottler, J., Sætran, L., Peinke, J., Adaramola, M., and Hölling, M.: Wind tunnel experiments on wind turbine wakes in yaw: effects of inflow turbulence and shear, Wind Energ. Sci., 3, 329–343, https://doi.org/10.5194/wes-3-329-2018, 2018. a
Bastankhah, M. and Porté-Agel, F.: A new analytical model for wind-turbine wakes, Renew. Energ., 70, 116–123, 2014. a, b, c, d, e, f, g, h, i
Bastankhah, M. and Porté-Agel, F.: Experimental and theoretical study of wind turbine wakes in yawed conditions, J. Fluid Mech., 806, 506–541, 2016. a, b, c
Boersma, S., Doekemeijer, B., Gebraad, P., Fleming, P., Annoni, J., Scholbrock, A., Frederik, J., and van Wingerden, J.: A tutorial on control-oriented modeling and control of wind farms, in: 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017, IEEE, 1–18, 2017. a
Campagnolo, F., Schreiber, J., Garcia, A. M., and Bottasso, C. L.: Wind Tunnel Validation of a Wind Observer for Wind Farm Control, International Society of Offshore and Polar Engineers, San Francisco, California, USA, ISOPE-I-17-410, 2017. a, b
Campagnolo, F., Petrović, V., Bottasso, C. L., and Croce, A.: Wind tunnel testing of wake control strategies, American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016, IEEE, 513–518, https://doi.org/10.1109/ACC.2016.7524965, 2016. a, b
Churchfield, M. J.: A Review of Wind Turbine Wake Models and Future Directions, in: 2013 North American Wind Energy Academy (NAWEA) Symposium, Boulder, Colorado, 6 August 2013. a
energiespektrum.de: Produzieren auf engem Raum, available at: https://www.energiespektrum.de/produzieren-auf-engem-raum-8918 (last access: 11 December 2019), 2015. a
Frandsen, S., Barthelmie, R., Pryor, S., Rathmann, O., Larsen, S., Højstrup, J., and Thøgersen, M.: Analytical modelling of wind speed deficit in large offshore wind farms, Wind Energy, 9, 39–53, 2006. a, b, c, d
Gebraad, P. M. O., Teeuwisse, F. W., van Wingerden, J. W., Fleming, P. A., Ruben, S. D., Marden, J. R., and Pao, L. Y.: A data-driven model for wind plant power optimization by yaw control, in: 2014 American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014, IEEE, 3128–3134, 2014. a
Jensen, N. O.: A note on wind generator interaction, Risø National Laboratory, Roskilde, M-2411, 1983. a
Jonkman, J. M. and Buhl Jr., M. L.: “FAST user's guide”, NREL/EL-500-29798, National Renewable Energy Laboratory, Golden, Colorado, available at: https://nwtc.nrel.gov/FAST7 (last access: 29 January 2020), 2005. a
Katić, I., Højstrup, J., and Jensen, N. O.: A simple model for cluster efficiency, in: European Wind Energy Association Conference and Exhibition, Rome, Italy, 7–9 October 1986, 407–410, 1986. a
Keane, A., Aguirre, P. E. O., Ferchland, H., Clive, P., and Gallacher, D.: An analytical model for a full wind turbine wake, J. Phys. Conf. Ser., 753, 032039, https://doi.org/10.1088/1742-6596/753/3/032039, 2016. a, b, c, d, e, f, g
Lagarias, J. C., Reeds, J. A., Wright, M. H., and Wright, P. E.: Convergence Properties of the Nelder–Mead Simplex Method in Low Dimensions, SIAM J. Optimiz., 9, 112–147, https://doi.org/10.1137/S1052623496303470, 1998. a
Peña, A., Réthoré, P.-E., and van der Laan, M. P.: On the application of the Jensen wake model using a turbulence-dependent wake decay coefficient: The Sexbierum case, Wind Energy, 19, 763–776, https://doi.org/10.1002/we.1863, 2016. a
Scholbrock, A. K.: Optimizing Wind Farm Control Strategies to Minimize Wake Loss Effects, Master's thesis, University of Colorado, Boulder, USA, 2011. a
Schreiber, J., Salbert, B., and Bottasso, C. L.: Study of wind farm control potential based on SCADA data, J. Phys. Conf. Ser., 1037, 032012, https://doi.org/10.1088/1742-6596/1037/3/032012, 2018. a
Wang, J., Foley, S., Nanos, E., Yu, T., Campagnolo, F., Bottasso, C., Zanotti, A., and Croce, A.: Numerical and Experimental Study of Wake Redirection Techniques in a Boundary Layer Wind Tunnel, J. Phys. Conf. Ser., 854, 012048, https://doi.org/10.1088/1742-6596/854/1/012048, 2017. a, b
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(1935 KB) - Full-text XML