the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Brief communication: A simple axial induction modification to the Weather Research and Forecasting Fitch wind farm parameterization
Lukas Vollmer
Balthazar Arnoldus Maria Sengers
Martin Dörenkämper
We propose a modification to the Fitch wind farm parameterization implemented in the Weather Research and Forecasting (WRF) model. This modification, derived from 1D momentum theory, employs a wind-speed-dependent induction factor to correct the local grid wind speed back to freestream before computing the turbine's power and thrust. While the original implementation underestimates power, the modified version shows good agreement with the power curve. We strongly recommend employing the modification for all studies that model at maximum one turbine per WRF grid cell. For simulations with more turbines per grid cell, additional inner-cell wake losses have to be considered.
- Article
(1363 KB) - Full-text XML
- BibTeX
- EndNote
As offshore wind energy is developing quickly and in relatively concentrated regions along the coastline, models that correctly represent large-scale wake effects and their interactions with the atmosphere are needed. Several attempts towards the realistic modeling of those effects have been made by employing fast engineering models (e.g., Nygaard et al., 2020), high-fidelity models (e.g., Wiegant and Verzijlbergh, 2019; Maas and Raasch, 2022) or mesoscale weather models (e.g., Lundquist et al., 2019; Siedersleben et al., 2018). The latter is being used by an increasing number of institutions (Fischereit et al., 2021).
The most commonly used mesoscale model, especially when studying large-scale wake effects, is the Weather Research and Forecasting model (WRF; Skamarock and Klemp, 2008; Skamarock et al., 2021). The wind farm parameterization proposed by Fitch et al. (2012) has been integrated into WRF's main code for approximately a decade, establishing itself as the most frequently utilized approach (Fischereit et al., 2021). It models wind farms as an elevated sink of momentum and a source of turbulent kinetic energy, assuming that thrust that is not converted to power linearly scales with the turbulence added to the flow.
The Fitch parameterization does not consider the effect induction has on the local wind speed at the grid cell of the turbine. In this publication we show that, as a consequence, the turbines' power and thrust are underestimated. Abkar and Porté-Agel (2015) mention that the local wind speed may deviate from the free wind speed that should be used for the calculation of forces and power production. However, they only discuss this effect for cases of multiple wind turbines in a grid cell and use high-fidelity simulations to compute a correction factor. A similar approach was suggested by Mayol et al. (2020), who introduced an induction-aware modification to the Fitch parameterization by computing a correction factor with idealized WRF simulations.
The effect of axial induction increases in relevance with increasing ratios between turbine dimensions and grid sizes. It is therefore desirable to have a method that does not rely on precomputed correction factors but rather one that is directly generalizable. This brief communication proposes a physics-derived modification based on 1D momentum theory. It considers the induction factor of the wind turbine to correct the local grid wind speed back to a freestream wind speed, as is standard in actuator disk modeling. The validity of the proposed modification is directly verified by comparing the model's power estimations to power curve calculations using the wind speed from a reference simulation without a turbine.
2.1 WRF setup
WRF version 4.2.1 was employed for this study. Note that this version already includes the bug fix to the Fitch parameterization reported by Archer et al. (2020). The simulation setup was largely based on Cañadillas et al. (2022). Three one-way nested domains, the smallest one having a spatial resolution of 2 km, were centered around a random point in the German Bight. Initial and boundary conditions were described every 6 h by ERA5, while the sea surface temperature was provided by OSTIA. The physics schemes used consists of the following: the MYNN 2.5 level planetary boundary layer scheme, the Noah land-surface model, the MYNN surface layer scheme, the RRTMG longwave and shortwave radiation schemes, the WRF single-moment five-class microphysics scheme, and the Kain–Fritsch cumulus scheme (only outer two domains).
We conducted a simulation of 5 d (21–25 January 2020), preceded by 24 h that was omitted as spin-up. A single turbine was placed in the domain, which was centered around the German Bight. To analyze the sensitivity of the power calculations to the turbine dimensions, two turbine types were used: the NREL 5 MW wind turbine (Jonkman et al., 2009) with a hub height of 90 m and a rotor diameter of 126 m and a 22 MW wind turbine with a hub height of 175 m and a rotor diameter of 290 m that was created by simple dimensional upscaling of the IEA 15 MW wind turbine (Gaertner et al., 2020). As a reference, a simulation without turbines was performed, from which wind speed time series at hub height were extracted for a direct calculation of power by means of the turbine's power curve.
2.2 Fitch modification
The Fitch parameterization calculates each turbine's power output P and its influence on the momentum equations using the following equations:
where u is the locally sampled wind speed in the grid cell in which the turbine is located, CT and CP are the turbine's wind-speed-dependent thrust and power coefficients, is the turbine's rotor area, and ρ is the standard air density. The coefficient CTKE, used to calculate the tendency of the turbulent kinetic energy (TKE), is derived from the known power and thrust coefficients by . These calculations are done for each turbine individually. When one grid cell contains multiple turbines, the resulting effect on the momentum equations is just a sum of the single-turbine contributions.
CT and CP are dependent on a freestream wind speed that is undisturbed by the presence of the turbine. In practice, measurements are taken at least 2.5 rotor diameter upstream of the wind turbine. As the current implementation of the Fitch equations samples the wind speed u inside the grid cell, this condition is not respected. To this end, we suggest a modification to the Fitch equations that is based on a correction of the local wind speed u of the grid cell in which the turbine is placed, by the induction factor a of the wind turbine. The aim is to obtain a free wind speed u∞ to be used in power and thrust calculations:
with
The induction factor a is calculated from the CT of the turbine. A correction function f is needed to calculate how much of the mesh cross-section is occupied by the turbine area A. Because turbine orientation and mesh orientation rarely align, we propose the following correction function, which considers the local wind direction δ at hub height:
where dx is the horizontal grid size, D the rotor diameter and δ the horizontal wind direction. The correction function f becomes when the wind vector, and thus the turbine orientation, is perpendicular to the mesh and when it is diagonal to the mesh. In the final set of equations, the wind speed variable u∞ replaces the locally sampled wind speed u in Eqs. (1) to (3).
For n wind turbines within one grid cell, the wind speed correction can be extended by multiplying each turbine's induction. Note that we consider here that each turbine in the grid cell faces the free wind speed, and no mutual wake interactions occur. The assumption is also only valid when all wind turbines are of the same type.
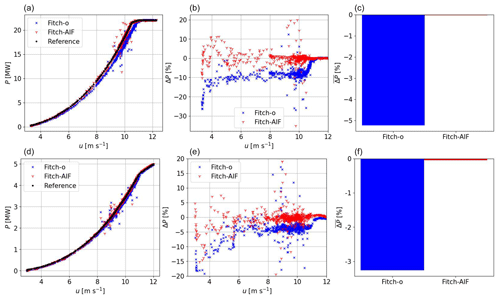
Figure 1Comparison of the 22 MW (a–c) and 5 MW (d–f) turbines modeled with different versions of the Fitch model and the reference. (a, d) Reconstructed power curves. (b, e) Power difference relative to the reference as a function of wind speed. (c, f) Mean power difference relative to the reference.
Figure 1 compares the calculated power of the reference, the original Fitch (Fitch-o) and the induction modification proposed here (Fitch-AIF). Figure 1a and d exhibit a reconstructed power curve and Fig. 1b and e the difference in both Fitch estimates relative to the reference. The scatter in these plots is due to the divergence between simulations as a result of, e.g., numerical approximations and the chaotic behavior of the atmosphere. Regardless, Fitch-o shows a clear systematic power deviation for wind speeds below rated, whereas Fitch-AIF exhibits values around zero. Averaged over the 5 d long simulation, Fig. 1c and f demonstrate that Fitch-o produces a significant error, which vanishes for Fitch-AIF. Moreover, the power difference is lower for the smaller turbine, which can be explained by the lower induction effect generated by the smaller turbine. Compared to Fitch-o, Fitch-AIF shows for the wind conditions during the simulated period a mean power and thrust increase of 5.5 % and 1.8 % respectively for the 22 MW turbine and 3.3 % and 2.0 % respectively for the 5 MW turbine. Due to the increased thrust, the wake deficits will also increase.
To demonstrate the scalability of the modification with high capacity densities and multiple turbines, five 22 MW wind turbines were placed within a single grid cell in WRF. While this scenario is rather unrealistic, it tests whether the proposed modification holds in extreme cases. Under the assumption that all five turbines operate in free wind conditions, the average power production per turbine calculated with the modification for multiple turbines (Fitch-mAIF) was compared with Fitch-o, Fitch-AIF and the reference (Fig. 2).
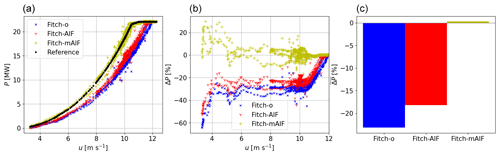
Figure 2Same as in Fig. 1 but for five 22 MW turbines per grid cell and with the addition of the Fitch-mAIF modification that combines the induction effect of the turbines within the grid cell for power calculation.
This exercise reveals that the underestimation of Fitch-o for this extreme dense case of turbines is about 23 %. This reduces to 18 % for Fitch-AIF but is almost eliminated when considering the number of turbines in the grid cell (Fitch-mAIF). The slightly positive in Fig. 2c is an artifact of the decorrelation of wind speeds between the simulations with and without turbines caused by the presence of the turbines. A longer simulation time would effectively eliminate this artifact and therefore does not affect AEP estimates from year-long simulations. Compared to Fitch-o, Fitch-AIF shows a power and thrust increase of 6.4 % and 3.3 %, while Fitch-mAIF displays increases of 30.6 % and 15.1 %. By showing that the modification is scalable to even these high capacity and turbine densities, we can infer that it also works for more realistic lower densities.
The Fitch wind farm parameterization implemented in WRF version 4.2.1 does not consider local induction effects and consequently underestimates power production of a single wind turbine in the dynamic region of the power curve. This issue is amplified for large turbines or when there are multiple turbines in one grid cell. To correct this underestimation, we propose a modification derived from 1D momentum theory. Instead of using the local wind speed of the grid cell, we use the wind-speed-dependent induction factor to estimate the freestream wind speed. Results from a simple analysis verify that the turbine's power curve is reproduced when including this modification, thus improving the power estimation of the wind turbine. Compared to measurement data, the power of a turbine will likely still differ from the simulated power by WRF, for example due to biases in the modeled wind speeds and power curves. A full-scale validation with measurement data is therefore considered important for future work. With the proposed induction correction, however, the model's negligence of the reduction in wind speed inside the grid cell due to the turbine's presence is not responsible for the difference anymore.
It is important to note that downstream wind speeds from wind farms modeled with WRF-Fitch have shown good agreement with measurements (Cañadillas et al., 2022; Fischereit et al., 2021). This implies that the Fitch model may be unintentionally generating correct results by ignoring induction as well as wake effects for grid cells containing multiple turbines. Instead of ignoring both effects, the reduction in thrust and power production of the cluster of turbines within a single grid cell due to inner-grid wake effects should be estimated, with the reference wind speed for the calculations being the induction-corrected wind speed. In this regard, the presented correction is just the first step towards a more correct wind farm parameterization within mesoscale models.
Solving the induction correction becomes challenging when turbines in a grid cell have different dimensions. In such cases, the non-dimensional thrust coefficient needs to be converted to dimensional form, and variations in hub heights need to be considered. However, if precise yield calculations for individual turbines are desired, the mesoscale model may not be the most suitable choice due to its low spatial resolution. Regardless, it is worth considering whether increasing the model resolution and allocating more computing resources are worthwhile to mitigate unresolved inner-grid effects.
In short, for scenario calculations of wind farm yields with wind farms of not more than one single turbine per cell (e.g., calculations involving future turbine dimensions), we strongly recommend using the proposed modification as presented in this paper for more accurate yield and wind resource assessments.
The WRF code with the induction correction for the Fitch parameterization is available for download at https://github.com/FraunhoferIWES/WRF.git (last access: 2 July 2024) (https://doi.org/10.5281/zenodo.12608856, Sengers et al., 2024).
LV conceptualized the idea, BAMS implemented the correction in WRF and performed the simulations. MD initiated the associated research project and was thus involved in the funding acquisition and discussions. All authors contributed significantly to the writing and reviewing of the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The results presented in this paper were derived within the framework of the X-Wakes (grant no. FKZ03EE3008) project. The X-Wakes project is funded by the German Federal Ministry for Economic Affairs and Climate Action (Bundesministerium für Wirtschaft und Klimaschutz – BMWK) due to a decision of the German Bundestag. The simulations were partly performed at the HPC cluster EDDY, located at the University of Oldenburg (Germany), and funded by the BMWK (grant no. FKZ0324005).
This paper was edited by Sukanta Basu and reviewed by Patrick Hawbecker and one anonymous referee.
Abkar, M. and Porté-Agel, F.: A new wind-farm parameterization for large-scale atmospheric models, J. Renew. Sustain. Energ., 7, 013121, https://doi.org/10.1063/1.4907600, 2015. a
Archer, C., Wu, S., Ma, Y., and Jimenez, P.: Two Corrections for Turbulent Kinetic Energy Generated by Wind Farms in the WRF Model, Mon. Weather Rev., 148, 4823–4835, https://doi.org/10.1175/MWR-D-20-0097.1, 2020. a
Cañadillas, B., Beckenbauer, M., Trujillo, J. J., Dörenkämper, M., Foreman, R., Neumann, T., and Lampert, A.: Offshore wind farm cluster wakes as observed by long-range-scanning wind lidar measurements and mesoscale modeling, Wind Energ. Sci., 7, 1241–1262, https://doi.org/10.5194/wes-7-1241-2022, 2022. a, b
Fischereit, J., Brown, R., Larsén, X. G., Badger, J., and Hawkes, G.: Review of Mesoscale Wind-Farm Parametrizations and Their Applications, Bound.-Lay. Meteorol., 182, 175–224, https://doi.org/10.1007/s10546-021-00652-y, 2021. a, b, c
Fitch, A. C., Olson, J. B., Lundquist, J. K., Dudhia, J., Gupta, A. K., Michalakes, J., and Barstad, I.: Local and Mesoscale Impacts of Wind Farms as Parameterized in a Mesoscale NWP Model, Mon. Weather Rev., 140, 3017–3038, https://doi.org/10.1175/MWR-D-11-00352.1, 2012. a
Gaertner, E., Rinker, J., Sethuraman, L., Zahle, F., Anderson, B., Barter, G., Abbas, N., Meng, F., Bortolotti, P., Skrzypinski, W., Scott, G., Feil, R., Bredmose, H., Dykes, K., Sheilds, M., Allen, C., and Viselli, A.: Definition of the IEA 15-Megawatt Offshore Reference Wind Turbine, https://www.nrel.gov/docs/fy20osti/75698.pdf (last access: 18 July 2023), 2020. a
Jonkman, J., Butterfield, S., Musial, W., and Scott, G.: Definition of a 5-MW Reference Wind Turbine for Offshore System Development, Tech. Rep. TP-500-38060, National Renewable Energy Laboratory, https://doi.org/10.2172/947422, 2009. a
Lundquist, J. K., DuVivier, K. K., Kaffine, D., and Tomaszewski, J. M.: Costs and consequences of wind turbine wake effects arising from uncoordinated wind energy development, Nat. Energ., 4, 26–34, https://doi.org/10.1038/s41560-018-0281-2, 2019. a
Maas, O. and Raasch, S.: Wake properties and power output of very large wind farms for different meteorological conditions and turbine spacings: a large-eddy simulation case study for the German Bight, Wind Energ. Sci., 7, 715–739, https://doi.org/10.5194/wes-7-715-2022, 2022. a
Mayol, M., Navarro Diaz, G., Saulo, A., and Otero, A.: An induction-aware parameterization for wind farms in the WRF mesoscale model, J. Phys.: Conf. Ser., 1618, 062006, https://doi.org/10.1088/1742-6596/1618/6/062006, 2020. a
Nygaard, N. G., Steen, S. T., Poulsen, L., and Pedersen, J. G.: Modelling cluster wakes and wind farm blockage, J. Phys.: Conf. Ser., 1618, 062072, https://doi.org/10.1088/1742-6596/1618/6/062072, 2020. a
Sengers, B., Vollmer, L., and Dörenkämper, M.: First release of Axial Induction Factor correction of WRF Fitch in v4.2.1, Zenodo [code], https://doi.org/10.5281/zenodo.12608856, 2024. a
Siedersleben, S. K., Platis, A., Lundquist, J. K., Lampert, A., Bärfuss, K., Cañadillas, B., Djath, B., Schulz-Stellenfleth, J., Bange, J., Neumann, T., and Emeis, S.: Evaluation of a Wind Farm Parametrization for Mesoscale Atmospheric Flow Models with Aircraft Measurements, Meteorol. Z., 27, 401–415, https://doi.org/10.1127/metz/2018/0900, 2018. a
Skamarock, W. C. and Klemp, J. B.: A time-split nonhydrostatic atmospheric model for weather research and forecasting applications, J. Comput. Phys., 227, 3465–3485, https://doi.org/10.1016/j.jcp.2007.01.037, 2008. a
Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Liu, Z., Berner, J., Wang, W., Powers, J. G., Duda, M. G., Barker, D. M., and Huang, X.-Y.: A Description of the Advanced Research WRF Model Version 4.3, Tech. Rep. TN-556+STR, National Center for Atmospheric Research, https://doi.org/10.5065/1dfh-6p97, 2021. a
Wiegant, E. and Verzijlbergh, R.: GRASP model description & validation report, https://www.dutchoffshorewindatlas.nl/binaries/dowa/documenten/reports/2019/12/05/whiffle-report---grasp-model-description-and-validation-report/grasp_description_validation.pdf, (last access: 19 June 2023), 2019. a





