Estimating the technical wind energy potential of Kansas that incorporates the effect of regional wind resource depletion by wind turbines

Energy scenarios require realistic estimates of technical wind energy potentials – estimates for how much electricity can be generated by wind turbines given a certain level of deployed capacity within a region. These are typically obtained using observed wind speeds, neglecting the depletion of the wind energy resource with increasing deployment at the regional scale. Here, we use the kinetic energy budget of the atmosphere (KEBA) approach to evaluate the importance of this resource depletion effect for the technical potential of Kansas, USA. To do so, we first apply the KEBA approach to a previously conducted set of numerical simulations with the Weather Research Forecasting (WRF) model. This set simulated the resource depletion effect for a range of different levels of wind turbine deployments within Kansas, which we use to test the KEBA approach. We specifically test the approach for nighttime and daytime conditions to capture the different mixing regimes of the atmospheric boundary layer. We find that KEBA can adequately capture the effect for both settings. We then extend our analysis by using ERA-5 forcing to the climatological scale. We find that this resource depletion effect increases almost linearly with the level of wind turbine deployment. Compared to previously published estimates for the technical potential for Kansas, the resource depletion effect lowers capacity factors by a third to a half. Since this resource depletion effect increases with installed capacity within a region, it is policy relevant even at relatively low deployment levels.

1 Introduction

Estimates of technical wind energy potentials are important for the design of energy transition pathways towards a future sustainable energy system (Prakash et al., 2019; Ruijgrok et al., 2019; GEA, 2012; IEA, 2021). They are inputs to integrated assessment models that deploy large-scale wind and solar systems and evaluate the impact of the integration of these variable sources into the electrical grid (Eurek et al., 2017). Technical potentials are defined as theoretical estimates of electrical generation from hypothetical regional-scale wind turbine deployments while accounting for areas that are actually available for wind energy development, wind turbine characteristics, and losses arising from inter-turbine interactions and energy conversion (Hoogwijk et al., 2004; McKenna et al., 2022; Manwell et al., 2010). The actual area available for wind energy development pertains to that over which wind turbines can be installed after accounting for technical, ecological, and social constraints (McKenna et al., 2022). A significant part of the policy relevance stems from the fact that technical potentials are a control on the economic costs of wind energy development (Blanco, 2009; Ragheb, 2017).

These resource potential estimates are especially distinct from the resource estimation performed for wind park planning and layout. The large scale at which these are estimated, typically spanning thousands of square kilometres with hundreds of gigawatts in deployed capacity, means that the detailed approaches used in wind park planning and layout, such as the Weather Research Forecasting (WRF) (Blahak and Wetter-Jetzt, 2010; Fitch et al., 2012; Volker et al., 2015; Boettcher et al., 2015), computational fluid dynamical (Wu and Porté-Agel, 2015), and engineering wake models (Katic et al., 1986; Frandsen et al., 2006; Pedersen et al., 2022), are not employed. The use of such comprehensive numerical models in energy scenario analysis is impeded by their need for high-performance-computing infrastructure and subject matter expertise (Staffell and Pfenninger, 2016). Thus, the typical approach for estimating technical potentials for application in energy scenario analyses and integrated assessment modelling is relatively straightforward in comparison to the more comprehensive approaches mentioned above. In this analysis, we use the term “standard approach” to refer specifically to this approach and not those employed for resource assessment for wind park planning and layout, which is outside the scope of this study.

The standard approach to estimating technical potential is to force a single wind turbine's power curve with observed or modelled time series of hub-height wind speeds. The potential then is a function of regional wind resource or wind speeds, turbine power curve, and the total number of wind turbines within the deployment area (Hoogwijk et al., 2004; Archer and Jacobson, 2005; Lu et al., 2009; Schallenberg-Rodriguez, 2013; Eurek et al., 2017; Enevoldsen et al., 2019). This approach differs from those typically employed in high-resolution evaluations of wind park planning and layout, primarily in its handling of energy generation and conversion losses. The standard approach fixes these losses typically to a value of about 10 % (Hoogwijk et al., 2004; Schallenberg-Rodriguez, 2013; Eurek et al., 2017). This stems from the implicit assumption that large-scale wind energy generation minimally impacts the regional wind resource. This leads to an expectation of a linear relationship between technical potential and capacity deployed. Further, it is implied that the efficiency of the wind turbine deployment measured in terms of the capacity factor or the ratio of actual to rated wind turbine generation remains constant relative to the size of the deployed capacity. Therefore, larger deployed capacities at the regional scale with better turbines are expected to always lead to a proportionate increase in the technical potential (Wiser et al., 2016).

However, meso- and synoptic-scale simulations of technical potentials from regional-scale deployments using numerical models of the atmosphere like WRF and general circulation models (GCMs) show that the standard approach significantly overestimates technical potentials and capacity factors when wind energy is intensively used at large scales (Adams and Keith, 2013; Miller et al., 2015; Miller and Kleidon, 2016; Volker et al., 2017; Agora Energiewende et al., 2020; Kleidon and Miller, 2020; Jacobson and Archer, 2012). These studies highlight that technical potentials and capacity factors do not scale linearly or remain constant with the deployed capacity. This sub-linear increase in technical potential and the erosion of the capacity factor result from the depletion of regional wind resources (Miller et al., 2015; Miller and Kleidon, 2016; Kleidon and Miller, 2020; Kleidon, 2021) because wind turbines remove kinetic energy (KE) from the boundary layer winds to generate electricity.

Wind resource depletion, or the reduction in wind speeds within and behind wind turbine deployments, has been observed in a variety of measurement data from currently operating wind farms (Rajewski et al., 2013; Bodini et al., 2017; Lundquist et al., 2014; Hasager et al., 2015; Platis et al., 2018; Ahsbahs et al., 2020; Nygaard and Newcombe, 2018; Nygaard et al., 2020). Also referred to as wakes, wind speed reductions can extend up to 50 km behind operating wind farms (Cañadillas et al., 2020; Lundquist et al., 2018). The reduced wind speeds interact with and reduce the electrical generation from downstream wind farms (Méchali et al., 2006; Schneemann et al., 2020; Maas and Raasch, 2023; Akhtar et al., 2021). Numerical simulations of this phenomenon also compare reasonably well with the observations (Mirocha et al., 2015; Aitken et al., 2014; Siedersleben et al., 2018; Fischereit et al., 2021). Thus, it can be assumed that the impact of wind resource depletion on wind energy generation will persist as the scale of wind turbine deployment is increased and, thus, must be incorporated into energy scenario analyses.

For this depletion effect to be incorporated into energy scenario modelling, it is necessary to scale the impacts up to the proposed regional deployment scales while balancing the constraints on computational complexity and ease of implementation, as highlighted by Staffell and Pfenninger (2016). This means that the key physics that shape the regional wind resource depletion and its impact on technical potential should be understood. For this we need to look at how kinetic energy is generated and transported towards the surface before it can be extracted by wind turbines or is dissipated by friction or wake dissipation.

To start, the wind energy of the large-scale circulation is predominantly generated within the free atmosphere by differences in potential energy due to differential solar radiative heating (Peixoto and Oort, 1992; Kleidon, 2021). The free atmosphere is defined as the part of the atmosphere that is above the planetary boundary layer and is not impacted by surface friction (AMS, 2024). KE from the free atmosphere is transported vertically downwards into the boundary layer by vertical mixing, the lowest layer of the atmosphere where most of the KE is dissipated (Stull, 2009). The turbines extract some of the KE which would otherwise have been dissipated by surface friction. Since the rate at which KE is transported into the boundary layer is limited, it leads to a fixed KE budget being available for driving motion within the boundary layer (Kleidon and Miller, 2020). This means that the extraction of KE by a large number of wind turbines leads to less KE being available for the motion of the winds and comes at the expense of the dissipation by surface friction. Put another way, wind turbines generate electricity by depleting the boundary layer KE resource even though this resource is renewed at a constrained rate. As a result, larger rates of KE extraction from a fixed KE input cause slower winds and reduced capacity factors (Miller et al., 2011).

This wind reduction effect is supported by mesoscale WRF simulations which show that technical potentials from onshore deployments larger than 100 km² are limited to yields of about 1.1 W m⁻² for very high turbine densities (Adams and Keith, 2013; Miller and Kleidon, 2016; Jacobson and Archer, 2012; Marvel et al., 2012; Gustavson, 1979; Wang and Prinn, 2010, 2011; Volker et al., 2017). This is in contrast to the standard approach, in which estimates range from 2–6 W m⁻²(Jacobson and Delucchi, 2011; Jacobson and Archer, 2012; Lu et al., 2009; Archer and Jacobson, 2005; Edenhofer et al., 2011; Capps and Zender, 2010). At the maximum potential, wind speeds are estimated to slow down by 42 %, while capacity factors reduce by ∼ 50 % relative to the standard estimate (Miller et al., 2015; Volker et al., 2017). A mean of 1.1 W m⁻² implies electricity generation of ∼ 900–1900 TWh yr⁻¹ if all the available area for wind energy in a windy area like Kansas (100 000–200 000 km⁻²), USA, is covered with wind turbines. These generation potentials are about a third lower than the standard expectation of 2000–3000 TWh yr⁻¹ (Brown et al., 2016; Lopez et al., 2012). Thus, the standard approach to technical potential estimation in energy scenario analyses needs to incorporate the effects of wind speed reductions arising from limitations imposed by the atmospheric KE budget.

A simple yet physical approach to deriving technical potential estimates that includes the effects of KE removal on wind speeds is to constrain the wind speeds and turbine yields with an explicitly defined KE budget of the atmospheric boundary layer. In this approach, known as the kinetic energy budget of the atmosphere (KEBA; Kleidon and Miller, 2020), first the budget available to the deployment is estimated from the sum of the vertical and horizontal KE fluxes over the deployment region. The vertical component represents the KE input into the boundary layer from the free atmosphere, while the horizontal component represents the boundary layer wind flow. Both rates can be estimated from wind speed observations but also depend on boundary layer height and surface friction. The reduction in wind speeds is estimated by accounting for the removal of KE from the budget. The slower wind speeds are then used to estimate turbine yields (Kleidon and Miller, 2020). This approach has previously been shown to compare well against numerical weather forecasting simulations of wind turbine deployments in idealized onshore weather conditions (Kleidon and Miller, 2020) and in real weather conditions in offshore areas in the German Bight of the North Sea (Agora Energiewende et al., 2020). In this study we will extend the regimes over which KEBA has been studied by applying it under realistic weather conditions in a prospective onshore region of Kansas.

We first evaluate the KEBA approach with a set of previous numerical simulations of hypothetical large-scale wind turbine deployment scenarios in Kansas, central USA (Miller et al., 2015). One interesting aspect of these simulations is the different response of resource depletion during night and day, presumably due to the different boundary layer mixing regimes. The simulations showed that wind speeds are typically 40 % lower during the day than at night (Fig. 1a), but overall daytime electrical yields were about 50 % higher than nighttime (Fig. 1c).

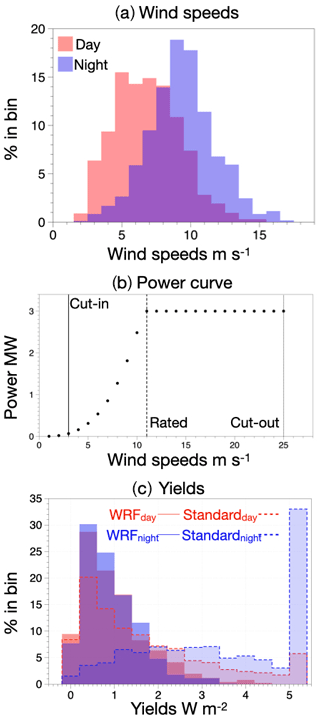
Figure 1 (a) Distribution of wind speeds averaged over a prospective deployment area in Kansas, central USA, for daytime (red) and nighttime (blue) in the absence of wind turbines. (b) The power curve for a Vestas V112 3 MW wind turbine used in this study. It does not generate electricity for wind speeds below the “cut-in” (3 m s⁻¹, solid black line) and above the “cut-out” wind speed (25 m s⁻¹, dotted black line). Yields vary with the cube of wind speeds below the “rated” wind speed (11 m s⁻¹, stippled black line) but remain at capacity above it. (c) Deployment yields during daytime (red) and nighttime (blue) for the 5 MW km⁻² scenario from an interactive WRF simulation (solid, WRF) and using the standard approach (dashed outlines). WRF estimates that the total deployment yield during the day (WRF_day = 63 GW) is higher than nighttime (WRF_night = 42 GW), while the standard estimate yields higher potentials and the opposite response (Standard_day = 109 GW, Standard_night = 159 GW). Data are taken from Miller et al. (2015).

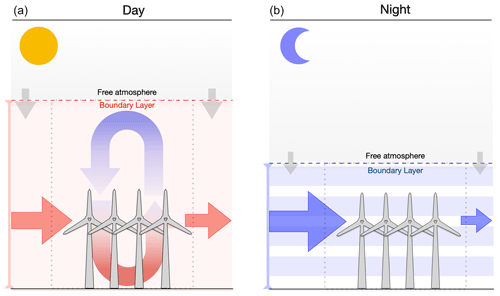
Figure 2 Differences between daytime (a) and nighttime (b) boundary layer conditions and their effect on the renewal of kinetic energy from the free atmosphere (grey arrows) and convective mixing (blue and red arrow in a). The red and blue arrows represent the horizontal kinetic energy in- and outflow (from left to right) through the boundary layer volume bounding the regional-scale wind turbine deployment (dotted box) during day and night, respectively. The free atmosphere represents the part of the atmosphere in which large-scale motion is generated in the absence of friction.

The result can be understood when one accounts for the effect of lower boundary layer heights and reduced mixing at night, which reduces the size of the kinetic energy budget (Fig. 2). As a result, the KE removal by the wind turbines has a stronger effect on wind speed reductions at night (Fitch et al., 2013a; Abkar et al., 2015). During the day, because the KE budget is larger, this depletion effect is proportionally smaller. Solar insolation drives vertical convection and the vertical growth of the boundary layer, resulting in higher downward replenishment of KE from the free atmosphere and a larger reservoir of KE in the boundary layer. The absence of solar-driven convection at night leads to stratified or stable conditions that restrict vertical KE replenishment. This leads to a greater reduction in wind speeds at night compared to the day and therefore lower yields despite higher incoming undisturbed wind speeds. Thus, the differences in boundary layer characteristics during day and night will affect wind resource potentials of regional deployments of wind turbines. This is an important test to evaluate with KEBA since the standard approach would estimate the opposite – higher nighttime yields due to higher wind speeds than during daytime – and therefore have a bias in technical potentials. The ability of KEBA to capture this counter-intuitive effect at the regional scale will clarify the relevance of KE removal at regional scales of wind turbine deployment and applicability of KEBA in regional wind energy resource assessment.

To identify the policy relevance of this depletion effect, we then extended our analysis to the climatological scale using ERA-5 reanalysis forcing (Hersbach et al., 2020). Because KEBA is computationally not expensive, we can then quantify the effect of wind resource depletion on different levels of installed capacity over a whole climatological period. By comparing these effects against the previous studies of the wind energy potential of Kansas (Lopez et al., 2012; Brown et al., 2016), we can then establish the policy relevance of this effect.

In the following section, we provide a brief description of the KEBA approach, the turbine deployment scenarios, and the model parameters used to test KEBA for the regional numerical WRF simulations over Kansas before we describe the setup with ERA-5 reanalysis to extend the insights to the climatological scale. The results section then diagnoses the kinetic energy budgets and the wind speed reductions for nighttime and daytime conditions and evaluates the effect on the wind turbine yields and capacity factors. We continue with an evaluation of the role of the boundary layer height in the estimates and discuss the limitations of the KEBA approach. We then present the results of the extension to the climatology and compare our estimate for the technical wind energy potential for Kansas to previously published estimates (Lopez et al., 2012; Brown et al., 2016) before we discuss the broader-scale implications of our analysis. We close with a brief summary and conclusions.

2 Methods

To estimate the technical wind resource potential with the resource depletion effect, we first use KEBA together with the wind fields of the numerical WRF simulation for Kansas without any wind turbines (Miller et al., 2015). Different scenarios of wind turbine deployments are then used in KEBA and compared to the respective WRF simulation, separately for nighttime and daytime conditions. We also compare these simulations to the standard approach, which is to say the estimate of the technical wind resource potential that uses wind fields and the turbine power curve but does not include the resource depletion effect. In the second step, we then apply KEBA to the wind fields of the ERA-5 reanalysis to quantify the resource depletion effect at the climatological scale.

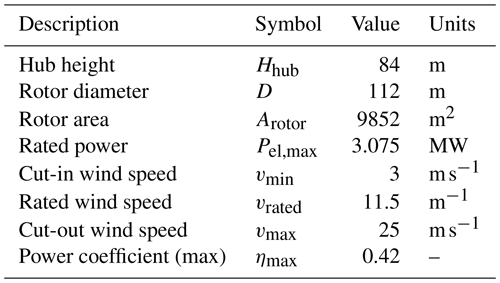
We first describe the standard and KEBA approaches, followed by the WRF simulations and the scenarios that are considered. All approaches need information for the power curve of the wind turbines being deployed. For this, we use the Vestas V112 3 MW turbine, as in the simulations by Miller et al. (2015). The characteristics of the turbine are summarized in Table 1. The last part of the methodology describes how the climatological resource potentials are derived using KEBA in combination with ERA-5 wind fields.

Table 1 Turbine characteristics of a Vestas V112 3 MW turbine, as in Miller et al. (2015).

2.1 The standard approach

The standard approach estimates the technical resource potential from the power curve, multiplied by the number of wind turbines N being considered:

$$\begin{array}{}\text{(1)}& P_{\text{el,std}}=N\cdot min\left(P_{\text{el,max}},{\displaystyle \frac{\mathit{\rho }}{\mathrm{2}}}\cdot {\mathit{\eta }}_{\text{max}}\cdot A_{\text{rotor}}\cdot v_{\text{in}}^{\mathrm{3}}\right),\end{array}$$

where ρ is the air density (we used ρ = 1.2 kg m⁻³), v_in is the wind speed, and the different turbine characteristics are given in Table 1. The deployment scenarios are described in the WRF subsection below.

2.2 The KEBA approach

The KEBA model (Kleidon and Miller, 2020) represents a budget of the KE fluxes of the boundary layer over the deployment region. Different levels of deployment alter the effective velocity v_eff within the region and result in a reduction factor f_red. This reduction factor is applied to the standard approach to account for the resource depletion effect.

The reduction factor f_red is directly derived from the KE budget. It is represented by

$$\begin{array}{}\text{(2)}& f_{\text{red}}={\displaystyle \frac{H+\mathrm{2}{C}_{\mathrm{d}}\cdot L}{H+\mathrm{2}{C}_{\mathrm{d}}\cdot L+\frac{\mathrm{3}}{\mathrm{2}}\cdot \frac{N}{W}\cdot {\mathit{\eta }}_{\text{max}}\cdot A_{\text{rotor}}}}\end{array}$$

for wind speeds v_in above the cut-in velocity v_min and below the rated velocity v_rated when the turbine output is proportional to the incoming wind speeds (Fig. 2b) and

$$\begin{array}{}\text{(3)}& f_{\text{red}}=\mathrm{1}-{\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}\cdot {\displaystyle \frac{\mathrm{1}}{H+\mathrm{2}{C}_{\mathrm{d}}\cdot L}}\cdot {\displaystyle \frac{H}{L}}\cdot {\displaystyle \frac{N\cdot P_{\text{el,max}}}{J_{\text{in,h}}}}\end{array}$$

for v_in greater than the rated velocity v_rated but below the cut-out velocity v_max. For this case, f_red is computed only to simulate the effect of wind speed reduction for comparison.

Table 2 Atmospheric and environmental specifications needed for the KEBA estimate.

Table 3 Scenarios of large-scale deployment of wind turbines in Kansas, central USA, evaluated here. Based on Miller et al. (2015).

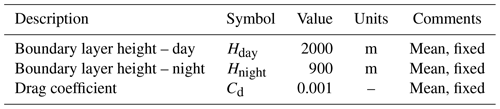
In the equations for f_red, H is the height of the boundary layer (Table 2), C_d is the aerodynamic drag coefficient of the surface (Table 2), L and W are the length and width of the deployment (Table 3), and J_in,h is the horizontal kinetic energy flux in the boundary layer ($\mathit{\rho }/\mathrm{2}\cdot v_{\text{in}}^{\mathrm{3}}\cdot WH$). The values for daytime and nighttime mean boundary layer heights are provided in Table 2. They were derived through the comparison of the vertical velocity profiles of the WRF simulations with and without the wind turbine deployment, yielding mean values of about 2000 m (day) and 900 m (night) (see Appendix A).

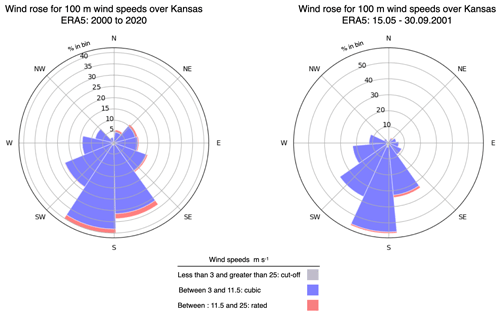
It should be kept in mind that the length and width of the deployment used in Eq. (3) can vary with wind direction, and this affects the equations for f_red. This implies that the reduction factor f_red can vary with wind direction. However, near-hub-height winds in Kansas typically come from the south (Fig. E1), meaning that most of the KE is transported from the south. Thus, we only use the dimensions that are relevant to this direction. The values of these parameters are specific for our analysis and may need to be adjusted for application elsewhere.

From this reduction factor, the resource potential is estimated similarly to the standard approach (Eq. 1), except for including the reduction factor f_red:

$$\begin{array}{}\text{(4)}& P_{\text{el,keba}}=N\cdot min\left(P_{\text{el,max}},f_{\text{red}}\cdot {\displaystyle \frac{\mathit{\rho }}{\mathrm{2}}}\cdot {\mathit{\eta }}_{\text{max}}\cdot A_{\text{rotor}}\cdot v_{\text{in}}^{\mathrm{3}}\right),\end{array}$$

where v_in is the unaffected wind speed in the absence of wind turbines.

Associated with this reduction is the effective velocity, which is given by

$$\begin{array}{}\text{(5)}& v_{\text{eff}}=f_{\text{red}}^{\frac{\mathrm{1}}{\mathrm{3}}}\cdot v_{\text{in}}.\end{array}$$

Note that in the case of f_red=1, KEBA represents the standard approach. This means the standard approach assumes that wind speeds remain unaffected by the large-scale extraction of kinetic energy (Eq. 5) and therefore that the electrical yield is proportional to the cube of the unaffected wind speeds (Eq. 1).

The kinetic energy budgets for the different scenarios are diagnosed from the time series of the velocity v_in and f_red and then averaged, with the different terms estimated as in Kleidon and Miller (2020). The budget is defined for the boundary layer air volume enclosing the deployment of wind turbines. The magnitude of the budget is set by the influx of kinetic energy, which is determined by the horizontal ($J_{\text{in,h}}=WH\cdot \frac{\mathit{\rho }}{\mathrm{2}}{v}_{\text{in}}^{\mathrm{3}}$) and vertical ($J_{\text{in,v}}=WL\cdot \mathit{\rho }{C}_{\mathrm{d}}{v}_{\text{in}}^{\mathrm{3}}$) influxes of kinetic energy into the volume. This energy is then either dissipated by surface friction, used for electricity generation, dissipated by wake turbulence, or exported downwind.

It should be noted that KEBA budgets the KE fluxes in the boundary layer over the entire wind turbine deployment with the aim of estimating the atmospheric response impacts on energy yield and wind speeds at the scale of a regional deployment. It does not attempt to model the horizontal or vertical variation in wind speeds or energy yields within the deployment. Therefore, the only forcing input needed is the wind speeds at the turbine's hub height v_in. This suffices because the turbine yields are a function of the hub-height wind speeds (Fig. 1b). The budget constraints on the boundary layer KE fluxes allow for the estimation of the wind speed reduction over the whole deployment, as expressed by the effective wind speed (v_eff). The reduced wind speeds can be thought of as that at which the deployment effectively operates when the KE flux budget constraints are accounted for. This approach is fit for our study despite being a simplified representation of the boundary layer and the atmosphere–turbine interactions. This is because we are only interested in evaluating the impacts of the atmospheric response on energy yields and wind speeds at the aggregate scale of the deployment. The evaluation of the finer variation within the deployment is not within the scope of our study. Further, it is also important to keep in mind that KEBA is simple in its formulation only compared to WRF. It is significantly more sophisticated in its representation of atmospheric physics relative to the standard approach.

2.3 WRF simulations

We use a set of sensitivity simulations with the WRF numerical weather simulation model (Miller et al., 2015). These simulations were performed with the WRF-ARW v3.3.1 model (Skamarock et al., 2008) to simulate different levels of hypothetical deployments of wind turbines over 112 × 10³ km² in Kansas (central USA) using atmospheric conditions from 15 May to 30 September 2001. The time period is representative of the typical summer season over Kansas typified by a near-neutral El Niño–Southern Oscillation (ENSO) phase and an average Great Plains low-level jet and summer soil moisture content (Miller et al., 2015). The WRF model adequately captures the horizontal and vertical variations in wind speeds over this period (Miller et al., 2015). Wind turbines are parameterized as elevated momentum sinks and sources of additional turbulent kinetic energy (TKE) (Fitch et al., 2013b). The large, idealized deployments simulated a range of installed turbine capacity densities from 0.3125 to 100 MW km⁻², which were equally distributed within the expansive wind farm area. The associated number of wind turbines is given in Tables B2 and B3.

We use these simulations for two reasons. First, we use the wind speeds from the simulation without turbines as inputs to the standard and KEBA approaches to estimate resource potentials, using the same set of scenarios. We then use the scenarios as the reference, in which the effects of wind turbines on the atmosphere are comprehensively accounted for, and refer to the wind resource estimate as the WRF estimate.

We restrict the comparison to a maximum installed capacity density of 10 MW km⁻², yielding a range of the total installed capacity of 35 GW to 1.1 TW over the region. Even though the 0.5 and 1.1 TW deployment scenarios can be considered extreme for Kansas, they are consistent with assumptions in published technical potential evaluations for the state (Lopez et al., 2012; Brown et al., 2016). The turbine characteristics and wind park scenarios, as well as the symbols used in the following, are summarized in Tables 1 and 3. It should be noted that the Miller et al. (2015) simulations prescribe the choice of parameter values in Table 1 and the turbine type (Fig. 1b) used here.

2.4 Climatological resource potentials

We estimate wind energy resource potentials at the climatological scale by using the hourly 100 m wind speed product from the ERA-5 reanalysis data set (Hersbach et al., 2020). Wind speeds from the state of Kansas over a 20-year period from the years 2000 to 2020 were selected for the analysis. The 100 m wind speed product has been chosen since it is close to the wind turbine hub height. The 20-year mean wind speed is around 6.7 m s⁻¹, which is lower than the 4.5-month mean wind speeds estimated from the WRF simulation (Fig. E3). The ERA-5 data set also shows that wind speeds come from the south almost 70 % of the time, making it the predominant wind direction (Fig. E1), with the result that we did not consider wind-direction-dependent values for W and L. These wind speeds are used to force the KEBA and standard approaches to estimate wind resource potentials and the depletion effect at the climatological scale.

We only estimate the technical potential and capacity factors for the 2.5 and 5 MW km⁻² scenarios, which are the ones that are consistent with the previous estimates from Brown et al. (2016) and Lopez et al. (2012). The KEBA setup for this calculation remains similar to that for the diurnal inter-comparison with the exception that only a single diurnal average boundary layer height of 1268 m is used (Miller et al., 2015). It should be kept in mind that ERA-5-based KEBA and standard estimates are likely to be lower than the WRF-based estimate because the ERA-5 wind speeds are lower (Fig. E3). However, this does not significantly affect our analysis since we are interested primarily in estimating the wind resource depletion effect and its policy relevance.

3 Results and discussion

We posited that the KE budget is central to understanding resource depletion effect of the large-scale deployment of wind turbines, including its manifestations in wind speed reductions and reduced capacity factors, and that this depletion effect differs between daytime and nighttime conditions. Therefore, we start by evaluating the KE budget and the effects on regional wind speeds and then describe the estimated yields and capacity factors. We perform a sensitivity analysis on boundary layer height to evaluate the effects of the day–night differences and compare these to the general effect of reduced wind speeds with greater installed capacities. We then discuss the limitation of the KEBA method before we re-evaluate the technical resource potential of Kansas. We close this section with a discussion of the broader implications.

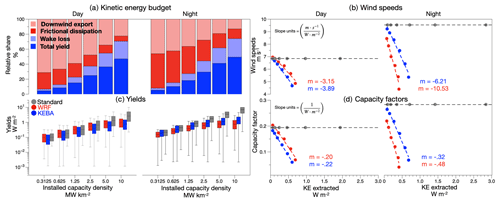
Figure 3 (a) Daytime (left) and nighttime (right) KE budgets with total yields (dark blue), wake loss (light blue), frictional dissipation (red), and the downwind export (light red). (b) Estimates of wind speeds over the deployment region against the KE extracted by the wind turbines for the standard (grey), WRF (red), and KEBA (blue) estimates. (c) Wind turbine yields as a function of installed capacity density using a logarithmic scale for the standard (grey), WRF (red), and KEBA (blue) estimates. (d) Capacity factors against the rate of KE extraction for the standard (grey), WRF (red), and KEBA (blue) estimates. Dashed lines in (b) and (d) denote linear fits. m denotes the slopes obtained from linear regression. The units for the slopes in (b) and (d) are $\left(\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}\right)(\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{)}^{-\mathrm{1}}$ and $(\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{)}^{-\mathrm{1}}$, respectively.

3.1 Kinetic energy budgets

The KE budget of the boundary layer volume enclosing the deployment is central to KEBA estimates, with the magnitude of the budget defining the wind speed reductions and limiting deployment yields. This budget is shown in Fig. 3a. The horizontal influx accounts for a larger share of the KE budget than the vertical input: 76 % during daytime and 60 % during nighttime. The combination of lower daytime wind speeds (v_day,mean = 6.8 m s⁻¹), higher daytime boundary heights (H_day = 2000 m), higher nighttime wind speeds (v_night,mean = 9.5 m s⁻¹), and lower nighttime boundary layer heights (H_night = 900 m) leads to similar influxes of kinetic energy of about 150 GW in the mean. The 150 GW budget sets the overall magnitude of the bars in Fig. 3a, with the distribution among the different terms changing due to the different deployment scenarios.

Within the boundary layer volume, KEBA determines the partitioning of the KE influx into frictional dissipation (red in Fig. 3a), wind turbine yields (dark blue), wake losses (light blue), and the downwind export of KE out of the deployment volume (light red). The KE extracted by wind turbines powers electricity generation (P_el,tot), with the wakes being dissipated by the mixing behind the turbines (D_wake). KE extraction utilizes KE that would have otherwise been dissipated at the surface by friction or exported downwind. Thus, the increase in capacity density increases yields and wake losses at the expense of KE in downwind export and frictional dissipation. Since individual turbine yields depend on wind speeds, higher nighttime mean wind speeds lead to higher per turbine yield compared to the daytime. Consequently, about 2 % more KE is extracted by the turbines from the budget at night than during the day (Fig. 3a).

3.2 Wind speeds

The depletion of the KE budget with increased wind turbine deployment is associated with a reduction in wind speeds. This reduction is shown in Fig. 3b, which shows how the mean wind speed over the deployment region (v_eff) reduces with the amount of KE extracted by the wind turbines (in W m⁻² of surface area). The KE extracted by the wind turbines is represented by the total yield of the deployment. Although the reduction in mean wind speeds with KE removed is not strictly linear, we utilize linear fits. The linear fit makes it easier to highlight key first-order effects, i.e. that reductions in mean wind speeds are higher when more KE is extracted and that reductions are steeper at night than during the daytime. Thus, the choice of linear fits emphasizes the first-order effects and eases the comparison between WRF, KEBA, and the standard approach.

Figure 3b shows these wind speed reductions for the WRF estimate (red) and the KEBA estimate (blue), while the standard approach (grey) assumes no change in wind speeds. The rates of reduction can be quantified by the slope m of the linear regressions (dashed lines). The slope is represented by units of $\left(\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}\right)(\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{)}^{-\mathrm{1}}$. Nighttime wind speed reductions (m_KEBA,night = −6.21) are almost twice as strong as during the day (m_KEBA,day = −3.89). These reduction rates are similar in the WRF estimates (m_wrf,night = −10.53, m_wrf,day = −3.15). Note that despite the faster rate of reduction in nighttime means, the wind speeds are nevertheless higher in magnitude than during the daytime. Compared to the WRF simulations, KEBA slightly overestimates daytime and underestimates nighttime wind speeds. Thus, the difference in daytime and nighttime wind speed reductions can be directly linked to the lower boundary layer height used in the nighttime KE budget in KEBA.

3.3 Deployment yields

Figure 3c shows the variation in the wind turbine yields with increasing installed capacity density. Since KEBA models yields as a function of the reduced wind speeds (v_eff) rather than the prescribed, unaffected wind speeds (v_in), its estimates (blue) are lower than the standard estimates (grey). KEBA estimates lower additional increments in yields with the increase in installed capacity during both day and night. Thus, the diminishing increments in yields with added turbines can be attributed directly to the reduced wind speeds shown in Fig. 3b. While KEBA estimates of nighttime yields are higher than daytime, WRF estimates of yield (red) are lower at night than during the day. KEBA captures the trends in yield increments but does not estimate the lower-than-daytime yields at night. It underestimates WRF's mean daytime estimates by 8 %–15 % while overestimating nighttime yields by 20 %–75 %. The standard estimate overestimates yields by up to 180 % during daytime and up to 600 % at night compared to the WRF estimates. The bias in KEBA estimates of yield compared to WRF can be attributed to higher nighttime KEBA wind speed estimates.

Figure 4 Daytime (a) and nighttime (b) total yields estimated by WRF (red ◦), KEBA with (blue ◦) and without (blue □) diurnal variations in boundary layer height, and the standard approach (grey ◦).

3.4 Capacity factors

The lower increments in deployment yields with increased installed capacity indicate that more turbines within the deployment region lower the mean efficiency of individual turbines. This can be shown by directly looking at the capacity factors, as displayed in Fig. 3d. Like Fig. 3b, capacity factors are plotted against the KE extracted by the turbines. The relationship between capacity factors and extracted KE is linear, and therefore the slope ($(\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{)}^{-\mathrm{1}}$) shows that the generation efficiency reduces as more KE is extracted from the atmosphere.

Both KEBA (blue) and WRF (red) estimates show that increasing KE extraction leads to lower capacity factors. The standard estimate (grey), however, assumes no change because no reduction in wind speeds is considered. The slopes of the linear regression show that turbine efficiencies reduce almost twice as fast during the night (m_KEBA,night = −0.32) than during the day (m_KEBA,day = −0.22), which is similar to the WRF estimates (m_wrf,night = −0.48 and m_wrf,day = −0.20). While KEBA, again, underestimates the strength of the reduction at night, the close match of KEBA estimates with the WRF estimates highlights that the removal of KE from the boundary layer is the main effect that results in reduced turbine efficiencies and wind turbine yields. KEBA is able to capture a large part of this trend because of the separate definition of day and night KE budgets as opposed to a single KE budget for the whole day.

3.5 Role of diurnal variations in boundary layer height

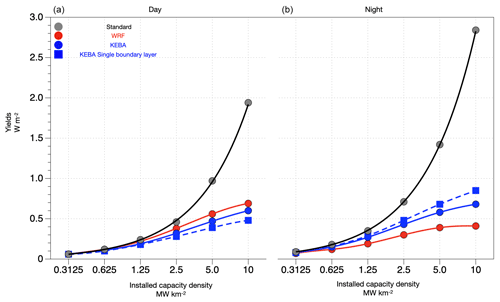
To evaluate how important the variation in boundary layer height is for estimating yields between day and night, we performed an additional estimate with KEBA in which the boundary layer height is fixed to the mean value of H = 1268 m (as in Miller et al., 2015). This comparison is shown in Fig. 4. Although the KEBA estimate with a single mean boundary layer height represents a substantial improvement over the standard estimate, it shows a greater discrepancy than the WRF estimate. Nighttime yields are overestimated by 20 % to 107 %, while daytime yields are underestimated by 12 % to 31 %. The addition of diurnal variations in boundary layer height improves the estimates relative to the WRF estimate, reducing the daytime bias to 10 % to 17 % and nighttime bias to 20 % to 60 %. The improvement is more pronounced for the nighttime conditions.

Defining different daytime and nighttime budgets separately is thus an improvement over neglecting this variation. It captures more of the underlying mechanism because the daytime solar insolation drives convective motion and higher mean boundary layer heights. The absence of these motions at night leads to much lower boundary layer heights. The difference in the amount of mixing between day and night differentially affects the wind speeds and deployment yields during day and night (Fitch et al., 2013a; Abkar et al., 2016). With all other variables in the KEBA model being fixed, a fixed boundary layer height in KEBA results in a 58 % lower daytime and 30 % higher nighttime KE budget compared to a variable boundary layer height.

Although the bias is not entirely compensated for by including the varying boundary layer heights in the KEBA estimates, this information clearly reduces the bias in the direction of the WRF estimate. However, the effect of these diurnal variations at the daily 24 h scale is relatively muted. This is because the higher daytime and lower nighttime generations largely compensate for each other, implying that it is mainly the role of KE removal that needs to be incorporated in the policy-focused estimation of technical potentials.

3.6 Limitations

This comparison between KEBA and the WRF estimates highlights some of the weaknesses of the KEBA approach. Although KEBA captures day and night trends produced by WRF better than the standard approach, it is unable to reproduce the full magnitude of the day–night difference. This is likely because KEBA does not account for stability conditions within the boundary layer (Kleidon and Miller, 2020). Since it only budgets the KE fluxes, it implicitly assumes that KE anywhere within the boundary layer is instantaneously available to the turbine. However, the real atmosphere transports KE via air masses, which means that the movement of KE to the turbine can be quick or slow depending on the stability conditions. Then, conceptually, KEBA can be thought of as being closer to the highly unstable condition than to the highly stable condition.

This assumption is valid during the day when the convective boundary layer is well-mixed. At night, however, stable conditions prevent vertical mixing because the insolation-driven convective motions are absent. The intensity of mixing within the boundary layer is thus an additional control on the rate at which the KE deficit behind wind turbines is replenished within the boundary layer. The less-mixed nighttime boundary layer slows the replenishment rate, leading to a steeper decline in wind speeds, capacity factors, and wind turbine yields (Fitch et al., 2013a; Abkar et al., 2016).

This interpretation is supported by observations of velocity deficits, or wakes, behind operating offshore wind farms that persist longer when the vertical mixing is lower (55km) than when it is higher (35km) (Cañadillas et al., 2020; Christiansen and Hasager, 2005). Longer wakes during less-mixed conditions imply lower downward replenishment than during better-mixed conditions, leading to the slower recovery of wind speeds.

The simulated daytime and nighttime mean wind speed reductions of 10 % and 30 % (Fitch et al., 2013a) from Kansas are similar to the estimates of Miller et al. (2015) of 17 % and 43 %. WRF estimates for wind turbine yields during day (42 % lower than standard) and night (73 % lower) are consistent with other simulations of idealized deployment yields over a full diurnal cycle, which found that reductions were twice as high at nighttime (57 %) than daytime (28 %) (Abkar et al., 2016). Thus, it is likely that the differences between WRF and KEBA could be reduced by accounting for stability effects, which could be taken up as a part of future work.

Additionally, the impact of more modern wind turbine technologies, i.e. higher turbines with larger capacities, on KEBA estimates has not been explicitly evaluated in our study. However, it is expected that our results remain largely similar in spite of improvements in turbine technology. An analysis of the resource potential of the German Bight (Agora Energiewende et al., 2020) showed that KEBA estimates of capacity factors were within 15 % of those obtained by WRF simulations even when taller and larger turbines were assumed (15 MW turbines with 150 m hub height).

Although KE fluxes are dependent on wind direction and these would have an effect on KEBA estimates, they have not been explicitly incorporated in our analysis. This was justified by the conditions in Kansas, which are dominated by winds from the south (see Fig. E1). In other regions, this may not be the case, and KE fluxes come from more than one dominant direction. This case could be represented in KEBA by using direction-dependent values of W and L, which would affect the reduction factor. This was, however, not tested here.

Despite these limitations, KEBA represents a significant improvement over the standard approach because on average it captures the impact of atmospheric response on yields during daytime and nighttime in a more comprehensive manner (Fig. 4). For the typical 2.5 and 5 MW km⁻² scenarios, KEBA's daytime and nighttime yield estimates are within ∼ 20 % and ∼ 50 % of WRF, respectively. In contrast, the standard approach overestimates WRF by up to ∼ 75 % and ∼ 265 % during day and night, respectively (Appendix Tables B2 and B3). This means that KEBA is more suitable for application at the climatological scale than the standard approach. Our results highlight the role of boundary layer information, in terms of height and mixing/stability in determining KE budgets that shape the extent to which wind speeds, turbine efficiencies, and deployment yields are affected by the removal of KE. Thus, KEBA appears to be a suitable tool to evaluate Kansas's technical wind energy potential.

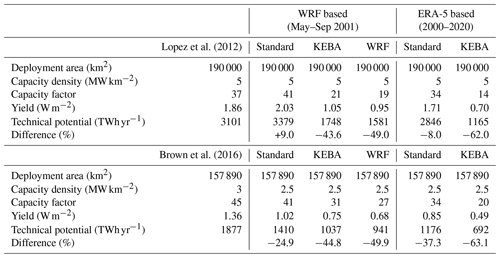
Table 4 Comparison of previously published estimates of the technical wind energy potential of Kansas by Lopez et al. (2012) and Brown et al. (2016) with the estimates from this study. There are two sets of estimates from this study: one based on WRF wind fields and the other using winds from ERA-5. For the comparison, we used the scenarios with installed capacity densities of 2.5 and 5 MW km⁻², which are close to the 3 and 5 MW km⁻² installed capacity densities used in the previous estimates.

3.7 Re-evaluating Kansas's technical potential

To quantify the relevance of these KE removal effects, we put the WRF and our KEBA estimates in context with previously published estimates of the technical potential of Kansas (Lopez et al., 2012; Brown et al., 2016). This is summarized in Table 4. Previous studies estimate potentials of 3101 and 1877 TWh yr⁻¹ for capacity densities of 5 and 3 MW km⁻² over 1.9 × 10⁵ and 1.6 × 10⁵ km², respectively, which include a fixed 15 % loss in array efficiency. This results in capacity factors of 37 % and 45 %. Expressed in terms of yields, these estimates imply 1.86 and 1.36 W m⁻² of generated electricity per unit surface area. Multiplied by the deployment areas, these yield technical potentials of 3101 and 1877 TWh yr⁻¹ for Kansas in these previous studies.

We first use the standard approach combined with the WRF and ERA-5 wind fields to estimate the resource potential to show that these are consistent with the estimates from the previous studies. We use installed capacity densities of 5 and 2.5 MW km⁻² as in our WRF simulations, which are similar to the installed capacity densities used in Lopez et al. (2012) and Brown et al. (2016). These result in average yields of 2.39 and 1.19 W m⁻², with a capacity factor of 48 % (see also Table B4). We reduce these estimates by the same 15 % loss as in the previous studies, which reduces the yields to 2.03 and 1.02 W m⁻², with a 41 % capacity factor. Multiplied by the deployment areas used in Lopez et al. (2012) and Brown et al. (2016), these yield technical potentials of 3379 and 1410 TWh yr⁻¹, which are close to the published estimates. Applying the standard approach to the ERA-5 wind fields results in lower average yields of 1.71 and 0.85 W m⁻², with a capacity factor of 34 %. The corresponding technical potentials are 2846 and 1176 TWh yr⁻¹, which are 8 % and 37 % lower than the previous estimates. These estimates are lower because 20-year ERA-5 wind speeds are on average lower than the WRF wind speeds (see Fig. E3).

We next demonstrate the relevance of the resource depletion effect. To do so, we use the KEBA and WRF estimates from above but apply these to the deployment areas of the previous studies. The KEBA estimate yields of 1.05 and 0.75 W m⁻² for the two scenarios, with capacity factors reduced to 21 % and 31 %, respectively. These estimates compare well with the WRF estimates of 0.95 and 0.68 W m⁻² and associated capacity factors of 19 % and 27 % (see also Miller et al., 2015). These result in technical potentials of 1748 and 1037 TWh yr⁻¹ for KEBA and 1581 and 941 TWh yr⁻¹ for WRF. These technical potentials are similar, demonstrating the ability of KEBA to reproduce the WRF results, but they are substantially lower than those reported by Lopez et al. (2012) and Brown et al. (2016). However, these apply only to the restricted time period of May–September 2001.

When we finally apply KEBA to the ERA-5 wind climatology, we obtain yields of 0.70 and 0.49 W m⁻² for the two scenarios, with associated capacity factors of 14 % and 20 %. These values are lower than for the WRF-based estimates because the climatological wind speeds are lower than those of the period considered with WRF. These result in technical resource potentials of 1165 and 692 TWh yr⁻¹, which are more than 60 % lower than the previously published estimates by Lopez et al. (2012) and Brown et al. (2016).

This re-evaluation and comparison to previous estimates demonstrate how significant the resource depletion effect is for adequately estimating the wind resource potential of a region but that this effect can be accounted for in a relatively simple way as represented by KEBA.

3.8 Implications for technical wind energy potential estimation

At the broader level, the reduction effects considered here are consistent with previous simulations by global and regional model simulations and have implications for the economic potential of wind energy. In the following, we first put our results with the resource depletion effect in the context of other studies before we estimate the consequences for the levelized costs of electricity.

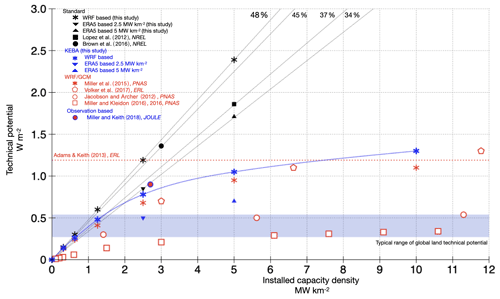
Figure 5 Technical potentials per unit surface area plotted against the capacity density (x axis). Black symbols represent standard estimates (no KE removal), while red symbols represent estimates with WRF or climate models (with KE removal). Blue symbols represent the KEBA estimates from this study. ERA-5-based estimates are represented separately with upward- (5 MW km⁻²) and downward-facing (2.5 MW km⁻²) triangles. The blue band represents the range of average peak global potentials (Miller et al., 2011; Jacobson and Archer, 2012; Miller and Kleidon, 2016; Marvel et al., 2012; Wang and Prinn, 2010, 2011; Gustavson, 1979). The dotted red line represents the peak average potential of Kansas (Adams and Keith, 2013), while the dotted lines show the capacity factors estimated without accounting for the removal of KE. Existing estimates of the Kansas resource potential are shown as filled black symbols (Brown et al., 2016; Lopez et al., 2012). The red circle with the blue outline shows an observation-based estimate (Miller and Keith, 2018).

These simulations generally show that when more wind turbines are deployed within a region, the technical potential increases less than what would be expected from a linear scaling. This less-than-linear response is due to the resource depletion effect. What it implies is that when the installed capacity within a region is, for instance, doubled, the expected yield will be less than twice the previous yield. This is shown in Fig. 5, in which the variation in technical potential in Kansas – in terms of the mean generated electricity per unit area – is plotted against the capacity density deployed. The diagram summarizes our estimates based on KEBA, WRF, and ERA-5, as well as previous studies that estimated the technical potential of Kansas but did not account for the resource depletion effect (Lopez et al., 2012; Brown et al., 2016) and also numerical model studies that accounted for the effect regionally (Adams and Keith, 2013; Volker et al., 2017) and globally (Miller et al., 2011; Jacobson and Archer, 2012; Miller and Kleidon, 2016; Marvel et al., 2012; Wang and Prinn, 2010, 2011; Gustavson, 1979). The dotted black lines represent in Fig. 5 the capacity factors, as these translate the installed capacity density into the mean technical potential. The lines thus represent the effect of assuming fixed capacity factors, so an increase in installed capacity translates into a proportionate increase in technical potential. What the various simulations show is that the resource depletion effect results in a less-than-linear response, which translates into reduced capacity factors with greater deployments. All the numerically simulated estimates display similar variations between potential and capacity and culminate near an average peak of about 1.1 W m⁻². This variation is also consistent with global estimates over land, albeit higher because Kansas is windier than most places (Miller et al., 2015). In line with these estimates, Miller and Keith (2018) showed that the actual yield from an average estimated onshore-US capacity density of 2.7 MW km⁻² is around 0.90 W m⁻². The agreement between estimates from independent numerical modelling studies and relevant observational data analysis points to the robustness of this effect.

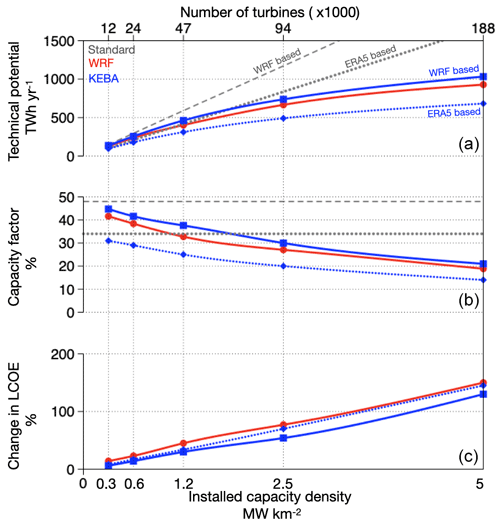
Figure 6 (a) Variation in WRF (red ◦), KEBA (blue □ with solid line, blue ⋄ with dotted line), and standard (grey stippled and dotted lines) estimates of technical potential, (b) capacity factors, and (c) percent change in the levelized cost of energy (LCOE) relative to the standard LCOE estimate plotted as a function of capacity densities (bottom) and number of turbines deployed (top). Standard and KEBA estimates based on WRF Control and ERA-5 data have been represented separately.

The variation in our KEBA estimates based on WRF and ERA-5 winds is consistent with these trends. Although the match between KEBA and the numerical estimates is not exact, it nevertheless captures the magnitude effect and reproduces the sub-linear scaling of technical potentials with installed capacity densities.

The reduced technical potentials and capacity factors significantly affect the economic potential of wind energy. This is commonly considered by evaluating the economic cost of wind energy using the levelized cost of energy (LCOE) (Ragheb, 2017; Blanco, 2009). We use the estimates from above and plot these in terms of a relative increase in LCOE in Fig. 6.

In the standard approach, based on its assumption of unaffected wind speeds, capacity factors remain constant, while the technical potential increases linearly. These are shown by the stippled and dotted grey lines depending on whether the estimate is based on WRF or ERA-5 (Fig 6a). Despite the difference in the slopes, both lines show that a doubling of capacity leads to a doubling of the potential. To estimate LCOE based on standard estimates, we assume that the cost of wind energy is only a function of the number of turbines. Then, LCOE becomes an inverse function of the capacity factor (see Appendix D). Thus, there is no change in the standard LCOE as the slopes of the line or the capacity factors remain unchanged.

In the resource depletion effect, however, technical potentials increase sub-linearly (Fig. 6a) and the capacity factors reduce (Fig. 6b). Each doubling of turbines from the lowest scenario to the 2.5 MW km⁻² scenario leads to an average of 70 %–75 % stepwise increase in potential factors coupled with an average of 11 %–14 % stepwise reduction in capacity factors. Each doubling in capacity beyond this leads to an average stepwise increment of 27 %–31 % in potential coupled with average reductions in capacity factors of 35 %–40 %. Since we assumed that LCOE is only inversely related to the capacity factor, capacity factor reductions lead to an LCOE increase relative to the standard LCOE estimate. Thus, the resource depletion effect leads to estimates of LCOE that are on average 130 %–150 % higher than the standard estimates at an installed capacity density of 5 MW km⁻².

Figure 6 highlights another important insight of this effect at lower installed capacity densities. The lowest capacity densities evaluated in this study (0.3125 and 0.625 MW km⁻²) are associated with reductions of around 6 %–12 % relative to the standard. These translate into corresponding relative increases of 6 %–23 % in LCOE, suggesting that the impacts of the resource depletion effect should be accounted for even in the case of sparser deployments.

Although the variation in technical potential, capacity factors, and LCOE with increasing capacity densities shown in Fig. 6 is idealized, the trend does have implications for realistic scenarios. The relationships in Fig. 6 provide a conceptual framework that quantitatively links the increase in generation from additional turbines with the degeneration of efficiency (i.e. capacity factor) and cost (i.e. LCOE) arising from physical constraints imposed by the atmosphere. Despite its idealized nature, the trends shown in Fig. 6 are consistent with real-world analyses that show that the capacity factor is the most important physical control on LCOE (Cory and Schwabe, 2009). Currently energy scenario analyses only anticipate an improvement in LCOE driven largely by improvements in capacity factors due to better turbine technology (Wiser et al., 2016; Prakash et al., 2019; Blanco, 2009). Figure 6 then motivates the evaluation of this expectation within the context of atmospheric limitations on KE availability for an improved estimate of LCOE.

Further, the trade-off between increased technical potential, capacity factors, and LCOE provides a strong physical constraint on installed capacity densities which, at present, range from 3 to 24 MW km⁻², thought mainly to be constrained by land availability (Hoogwijk et al., 2004; Lopez et al., 2012; Brown et al., 2016; Eurek et al., 2017; Enevoldsen et al., 2019; Lütkehus et al., 2013). The physical constraint indicates that there is a likely region-specific optimum installed capacity density which balances technical potential, capacity factors, and LCOE. Thus, even though Fig. 6 represents idealized relationships, it still provides a physically consistent conceptual framework that encapsulates the non-trivial impacts of the wind resource depletion on large-scale wind energy generation for application in energy scenario analyses. As we have shown, these impacts can be incorporated in energy scenario analyses almost completely by accounting for the KE removal effect.

4 Conclusions

We conclude that the impact of the KE removal effect on the technical wind energy potential of regional-scale wind turbine deployments is significant. Although daytime and nighttime boundary layer heights and stability conditions affect the technical potential, it is the removal of KE by the wind turbines that primarily shapes the reduction in wind speeds and capacity factors. It leads to reduced potentials compared to the standard approach that have a significant impact on the economic potential of wind energy at the regional and larger scales.

These impacts need to be assessed in policy evaluations of wind energy and the energy transition. KEBA is a viable alternative to the standard approach because it is simple to implement (Kleidon and Miller, 2020) and accounts for the effect of the key atmospheric control on technical potentials. This is not to negate the use of more physically comprehensive numerical methods like WRF and GCMs in policy analyses. Yet it enables energy scenario modellers without a background in meteorology to be able to incorporate the key physics without significantly increasing their models' computational complexity. The heavy computational requirements associated with numerical weather simulation models have been reported to inhibit their widespread incorporation into policy-side evaluations (Staffell and Pfenninger, 2016).

Lastly, despite these detrimental effects at larger deployment scales, KEBA's estimates agree with previous research that has shown that wind energy is nevertheless an abundant and renewable resource that can be used to meet a significant part of the future energy demand through efficient, large-scale deployment of wind turbines (Jacobson and Archer, 2012; Volker et al., 2017).

Appendix A: Determining boundary layer heights for KEBA

The KEBA model estimates park yield and mean wind speed reduction through the application of the conservation of energy (Kleidon and Miller, 2020). The kinetic energy (KE) generated in the atmospheric boundary layer is balanced by that consumed by the wind turbines within the wind park, its wake, the dissipation at the surface, and that which powers the remnant wind. The KE conservation is applied to a hypothetical boundary layer volume which encompasses the wind turbine deployment and is mathematically represented as $J_{\text{in,v}}+J_{\text{in,h}}=P_{\text{el,keba}}+P_{\text{wake}}+D_{\text{surface}}+J_{\text{out,h}}$. The left-hand side of this equation describes the horizontal and vertical flux of KE into the boundary layer volume, while the right-hand side describes how this is partitioned within the volume. The vertical and horizontal KE fluxes into the volume can be expanded to $J_{\text{in,v}}=WL\cdot \mathit{\rho }{C}_{\mathrm{d}}\cdot v_{\text{in}}^{\mathrm{3}}$ and $J_{\text{in,h}}=WH\cdot \frac{\mathit{\rho }}{\mathrm{2}}\cdot v_{\text{in}}^{\mathrm{3}}$.

These expressions show that the KE budget available to the wind turbine deployment is dependent on its geometry (crosswind width W and downwind length L) and the height of the atmospheric boundary layer (H). In our analysis, the geometry of the deployment is fixed; therefore the only control on the KE budget is the boundary layer height. Changes in boundary layer height affect the horizontal input of KE flux (J_in,h). In line with the general definition of the atmospheric boundary layer as the layer which responds quickly to changes in surface forcing (Stull, 2009), the boundary layer from a KE perspective can also be defined as a layer, the kinetic energy content of which responds to changes in surface forcing, i.e. the presence of large wind turbine deployments. Then the boundary layer height can be understood as the maximum height up to which the effects of kinetic energy removal by the turbines can be observed. Since the extraction of KE reduces mean wind speeds, changes in mean wind speeds induced by the turbines can be used to estimate this height.

The mean wind speeds over the region of interest, Kansas in this case, were extracted by Miller et al. (2015) from their WRF simulations. Mean wind speeds were estimated per vertical model level over Kansas for the time period of simulation. Such mean wind speed estimates were computed for all WRF simulations, i.e. those without wind parks (CTRL) and those with (0.3125–100 MW_i km⁻²). These mean wind speeds from the different models when plotted against model height (m) highlight the vertical variation in mean wind speeds or the vertical wind speed profiles. These are plotted for day and night separately in Fig. A1. In both the plots, the vertical wind speed profiles for the CTRL simulation represent the background circulation in the absence of any wind turbines and hence represent the undisturbed circulation. Vertical wind speed profiles for other simulations deviate from the CTRL trend because turbines extract KE from the wind speeds, thus slowing them down. The larger the number of turbines within the wind park, the greater the deviation from the CTRL or the undisturbed trend is. The mean day and night boundary layer heights for initializing the KEBA model are then those at which the vertical profiles derived from simulations with wind parks realign themselves with the undisturbed trend. Using this approach Miller et al. (2015) estimated the daytime boundary layer height to be 2000 m and the nighttime boundary layer height to be 900 m.

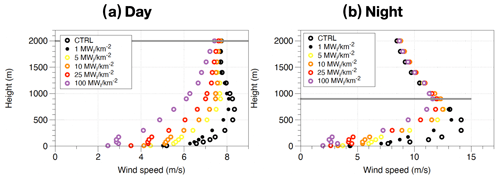
Figure A1 Daytime and nighttime vertical wind speed profiles estimated by Miller et al. (2015) which show that mean daytime boundary layer height is 2000 m, whereas that at night is 900 m.

Appendix B: Tables with data used in figures

B1 Wind speed reductions

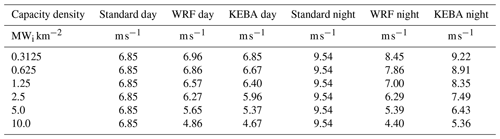
Here we tabulate (Table B1) the mean wind speed data simulated by Miller et al. (2015) without any wind parks or control (CTRL), as well as with the impact of wind parks with a range of turbine densities (0.3125–10 MW_i km⁻²) split by day and night. Along with it we also provide the mean wind speed reductions estimated by KEBA with different day and night mean boundary layer heights.

Table B1 This table shows wind speed predictions by WRF and KEBA split by day and night. The column entitled “standard” represents the CTRL wind speeds, i.e. without the impact of reduced wind speeds, since the standard approach predicts no change to mean wind speeds despite removal of kinetic energy. Thus day and night winds speeds remain constant and the same as the CTRL wind speeds.

B2 Park yield and capacity factors

This section presents tables containing information about park yields and capacity factors estimated by Miller et al. (2015) (WRF) and by us using the standard approach and the two different implementations of KEBA, i.e. with a single boundary layer height (KEBA single) and another with two different average heights (KEBA variable) for day (2000 m) and night (900 m) for the 0.3125–10 MW km⁻² capacity density scenarios. Tables B2 and B3 contain the data split between daytime and nighttime, respectively, whereas Table B4 contains the undifferentiated data.

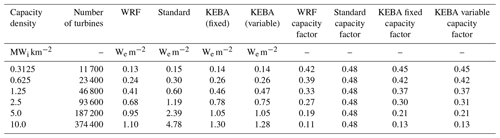
Table B2 Daytime averages. This table shows all the capacity density scenarios modelled, associated number of turbines, and park yields (WRF) modelled by Miller et al. (2015). It also shows the park yields estimated in this study using the standard approach, KEBA with a single boundary layer height (KEBA single), and KEBA with different average daytime and nighttime boundary layer heights (KEBA variable). The computed capacity factors, represented as fractions, from all the approaches are also included.

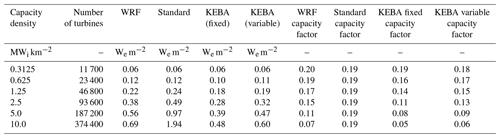
Table B3 Nighttime averages. This table shows all the capacity density scenarios modelled, associated number of turbines, and park yields (WRF) modelled by Miller et al. (2015). It also shows the park yields estimated in this study using the standard approach, KEBA with a single boundary layer height (KEBA single), and KEBA with different average daytime and nighttime boundary layer heights (KEBA variable). The computed capacity factors, represented as fractions, from all the approaches are also included.

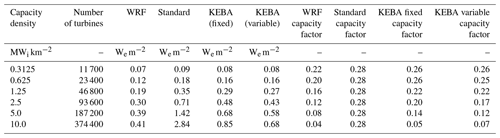
Table B4 Daily averages. This table shows all the capacity density scenarios modelled, associated number of turbines, and park yields (WRF) modelled by Miller et al. (2015). It also shows the park yields estimated in this study using the standard approach, KEBA with a single boundary layer height (KEBA single), and KEBA with different average daytime and nighttime boundary layer heights (KEBA variable). The computed capacity factors from all the approaches are also included.

Appendix C: Comparison with published numerical-weather-model-based estimates of technical wind energy potential

In Fig. 5, we have compared KEBA estimates of technical potential from our analysis with those performed independently by others over comparable regional and global scales using different numerical modelling approaches. For comparison in Kansas, central USA, we used the studies performed by Adams and Keith (2013), Miller et al. (2015), and Volker et al. (2017). From Volker et al. (2017), we only use their estimates for their largest deployment scenario (10⁵ km²) in the central USA. This was the most pertinent case for our analysis. All three of these studies use a version of WRF to model the wind turbine yields and parametrize the wind turbines as momentum sinks. This means that they account for the fact that turbines extract momentum and kinetic energy from the wind, thereby lowering wind speeds. While Miller et al. (2015) and Adams and Keith (2013) use a variation of the Fitch scheme (Fitch et al., 2013b), Volker et al. (2017) use the extended wake parameterization or the explicit wake parameterization (EWP) scheme (Volker et al., 2015). The main difference between the Fitch scheme, its variation, and the EWP is that, while the latter does not include an explicit term to account for the turbulent kinetic energy (TKE) generated by the turbine, the former two do. The different schemes lead to differences in the amount of mixing generated within the boundary layer due to the turbine action. The Fitch scheme estimates more and the EWP relatively less, even though their estimates of wind speeds largely agree with each other (Volker et al., 2015).

It is important to appreciate these differences because Archer et al. (2020) highlighted two bugs in the implementation of the Fitch scheme in WRF versions prior to v4.2 that affect the Miller et al. (2015) study (Fischereit et al., 2021). It was shown that the additional term in the Fitch scheme adds excessive TKE and a coding bug prevents the TKE from being advected properly. Although preliminary analyses have shown that the two errors actually compensate for each other, giving rise to TKE estimates that agree with observations (Archer et al., 2020; Larsén and Fischereit, 2021), it would be useful to briefly evaluate any potential implications for our results and conclusions.

First, according to a review by Fischereit et al. (2021) the conclusions of none of the three studies used in this study (Adams and Keith, 2013; Miller et al., 2015; Volker et al., 2015) are affected by the identified bug. Secondly, were these studies affected by the bug or the impact significant, one would have expected a more prominent deviation between the Fitch-based studies and the EWP-based study. This is because the EWP scheme does not use the explicit TKE addition term which the bug was related to. Instead, it is observed that the different studies exhibit a similar trend of technical potential with installed capacity that culminates in a peak average of 1.1 W m⁻².

Further, the WRF trends in Kansas, central USA, are consistent with previous studies that estimate global potentials. Relevant estimates of global land from Jacobson and Archer (2012) and Miller and Kleidon (2016) are shown in Fig. 6. These estimates and trends have been derived using global circulation models (GCMs): Jacobson and Archer (2012) used the GATOR-GCMOM model (Jacobson, 2001), while Miller et al. (2015) used the Planet Simulator model (Fraedrich et al., 2005). These are also unaffected by the errors in the Fitch scheme. These trends show the same variation in potentials as the WRF trends, i.e. sub-linear increase in potential beyond 1.5 MW km⁻² and culmination in a peak global average range of 0.2–0.6 W m⁻² (Miller et al., 2011; Miller and Kleidon, 2016; Jacobson and Archer, 2012; Wang and Prinn, 2010, 2011; Marvel et al., 2012). The agreement between all the independent trends and regional and global scale highlights that the impact of the errors in the Fitch scheme are unlikely to affect the insights and conclusions generated from this study.

Appendix D: Technical potential, capacity factors, and levelized cost of energy (LCOE)

Figure 6b shows that as the number of turbines deployed over the hypothetical wind farm area increases, the removal of kinetic energy (KE) reduces the capacity factor. This means that with the increasing deployed capacity, each turbine produces less energy than what it would have, had it been operating in isolation. The reduction in per-turbine efficiency increases with increasing turbines. When the KE removal is neglected, the capacity factor remains unchanged (dotted grey line). While the addition of turbines generally increases the technical potential, the step-wise increments in generation reduce as the turbine numbers increase (Fig. 6a). The lower increments are driven by the reductions in capacity factors (Fig. 6b). The effect of this variation in capacity factors can be used to investigate their economic impacts using a standard economic cost metric known as the levelized cost of energy or LCOE (Ragheb, 2017). LCOE is represented by the following formula (Ragheb, 2017):

$$\begin{array}{}\text{(D1)}& {\mathrm{LCOE}}_{\mathrm{wind}}={\displaystyle \frac{\begin{array}{c}{\sum }_{t=\mathrm{1}}^n(I_t+{\text{O\&M}}_t-{\text{PTC}}_t\\ -D_t+T_t+R_t)\cdot \frac{\mathrm{1}}{(\mathrm{1}+i{)}^t}\end{array}}{\text{CF}\cdot {\sum }_{t=\mathrm{0}}^{t=n-\mathrm{1}}{P}_t}}.\end{array}$$

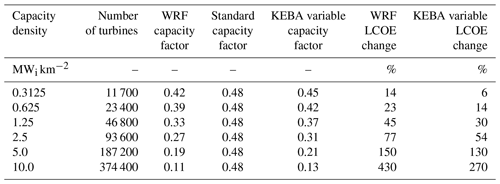
Table D1 Tabulation of capacity factors estimated by KEBA, WRF, and the standard approach along with the estimated change in LCOE (%) due to KE removal relative to the standard approach.

In this equation, I_t and O&M_t refer to the capital and operations cost, while PTC_t, D_t, T_t, and R_t represent the credits, levies, taxes, and royalties, respectively. The term $\frac{\mathrm{1}}{(\mathrm{1}+i{)}^t}$ is the present value factor which is used to account for the time value of money with a discount factor i over the lifespan of a wind farm. t represents a year within the operational period of a wind farm. CF is the capacity factor, which in this calculation would be different for different scenarios for WRF and KEBA but the same for the standard approach. Since we are interested in simply illustrating only the economic impact of reductions in capacity factors due to KE removal, we can simplify Eq. (D1) such that LCOE is only a function of capacity factor. For this, we ignore tax-related terms and assume that all costs and installed capacity terms (P_t) are sunk and installed once at the beginning of the operational life. The time factor also remains constant for all scenarios. It should be noted that this calculation is meant only to illustrate that capacity factor reduction arising from KE removal results in non-trivial increases in LCOE, which highlights their inclusion into the policy design. In reality, turbine installation will occur over many years and so will the cost investments. A real LCOE calculation would need specific and quality-controlled inputs about the timing and values of costs, levies, and discount rates. With the simplification, Eq. (D1) would take the following form:

$$\begin{array}{}\text{(D2)}& {\mathrm{LCOE}}_{\mathrm{scenario}}={\displaystyle \frac{\mathrm{1}}{{\mathrm{CF}}_{\mathrm{scenario}}}}\times \text{constant}.\end{array}$$

In Eq. (D2), LCOE for each capacity density scenario is inversely related to the capacity factor. As the cost and installed capacity terms are the same for the standard and the WRF and KEBA approaches, the percent change relative to the standard approach for each scenario can be calculated. These values for each of the installed capacity density scenarios are plotted for both WRF and KEBA estimates. For example, for the 2.5 MW km⁻² case the standard approach assumes a 0.48 capacity factor, while KEBA and WRF estimate 0.31 and 0.27. Then, to estimate the percent change relative to the standard approach, the following approach is used:

$$\begin{array}{}\text{(D3)}& \mathit{\%}\mathrm{change}\mathrm{in}{\mathrm{LCOE}}_{\mathrm{2.5}}={\displaystyle \frac{\begin{array}{c}{\text{LCOE}}_{\mathrm{2.5},\text{KEBA}/\text{WRF}}\\ -{\mathrm{LCOE}}_{\mathrm{2.5},\mathrm{standard}}\end{array}}{{\mathrm{LCOE}}_{\mathrm{2.5},\mathrm{standard}}}}.\end{array}$$

These values are tabulated in Table D1.

The change in LCOE is only calculated for the installed capacity range from 0.3125 to 10 MW km⁻² because this is the range that is typically assumed in wind energy policy scenarios. They show that as the capacity factor reduces, the economic cost of wind energy goes up because each of the turbines performs less efficiently.

Appendix E: KEBA and standard estimates based on ERA-5 100 m wind speeds from 2000–2020

Figure E1 Wind directions for 100 m wind speeds over Kansas from ERA-5 over the 2000–2020 period.

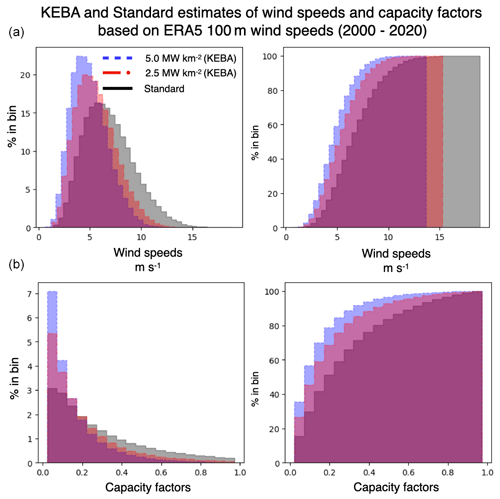
Figure E2 Wind speed (a) and capacity factor (b) distributions for standard and KEBA approaches for the 2.5 (red) and 5 MW km⁻² (blue) deployment scenarios calculated using ERA-5 100 m wind speeds over the 2000–2020 period.

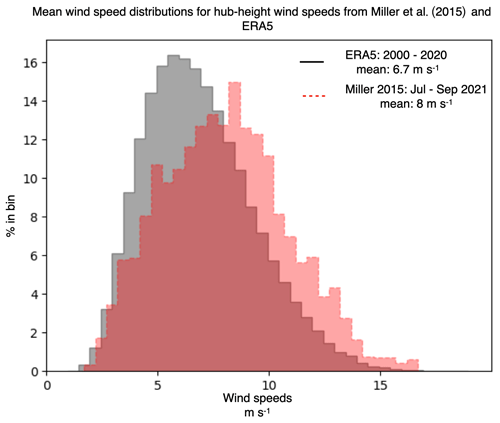
Figure E3 Comparison of near-hub-height wind speed distributions from Miller et al. (2015) (4.5 months, red) and ERA-5 (20 years, grey).