the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Initial results from a field campaign of wake steering applied at a commercial wind farm – Part 1
Jennifer King
Katherine Dykes
Eric Simley
Jason Roadman
Andrew Scholbrock
Patrick Murphy
Julie K. Lundquist
Patrick Moriarty
Katherine Fleming
Jeroen van Dam
Christopher Bay
Rafael Mudafort
Hector Lopez
Jason Skopek
Michael Scott
Brady Ryan
Charles Guernsey
Dan Brake
Wake steering is a form of wind farm control in which turbines use yaw offsets to affect wakes in order to yield an increase in total energy production. In this first phase of a study of wake steering at a commercial wind farm, two turbines implement a schedule of offsets. Results exploring the observed performance of wake steering are presented and some first lessons learned. For two closely spaced turbines, an approximate 14 % increase in energy was measured on the downstream turbine over a 10∘ sector, with a 4 % increase in energy production of the combined upstream–downstream turbine pair. Finally, the influence of atmospheric stability over the results is explored.
- Article
(6641 KB) - Full-text XML
- Companion paper
- BibTeX
- EndNote
This work was authored by the National Renewable Energy Laboratory, operated by the Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under contract no. DE-AC36-08GO28308.
The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.
Wind farm control is a field of research in which the control actions of individual turbines are coordinated to improve the total performance of the wind farm as defined by the total power production of the wind farm and the loads experienced by downwind turbines. Wake steering is a form of wind farm control wherein an upstream turbine intentionally offsets its yaw angle with respect to the wind direction to benefit downstream turbines (Wagenaar et al., 2012; Dahlberg and Medici, 2003).
Wake steering has been studied through wind tunnel studies (e.g., Medici and Alfredsson, 2006; Park et al., 2016; Schottler et al., 2017; Bartl et al., 2018), and large-eddy simulation (LES) studies of wake steering have been undertaken to date (see, for example, Fleming et al., 2015; Vollmer et al., 2016; Howland et al., 2016). Coupled with theoretical derivations, the results of the previously mentioned studies have enabled the development of control-oriented engineering models of wakes and wake steering that can be used to design and analyze wake steering controllers for wind farms and predict the performance benefit. Important examples include the Jensen wake model (Jensen, 1984) and the model of wake steering by Jiménez et al. (2010).
Flow Redirection and Induction in Steady State (FLORIS; NREL, 2019) is a software repository that provides an engineering model of wake steering that can be used in the design and analysis of wind farm control applications (Gebraad et al., 2016). Originally based on Jensen (1984) and Jiménez et al. (2010), it now employs the wake recovery and redirection models of Bastankhah and Porté-Agel (2014, 2016) and Niayifar and Porté-Agel (2015). Annoni et al. (2018) provide a detailed description of the current FLORIS model. The FLORIS model is open source and available for download and collaborative development (https://github.com/nrel/FLORIS, version 1.0.0, last access: 1 May 2019). Development is ongoing, and future models will incorporate the advances proposed in Martínez-Tossas et al. (2018).
Critical to advancement, improvement, and eventual adoption of wake steering are field trials of wake steering in realistic environments. Wagenaar et al. (2012) attempted wake steering at a scaled wind farm. One important campaign took place at the National Wind Technology Center in Boulder, Colorado. In that study, a rear-facing scanning lidar from the University of Stuttgart was placed on top of the nacelle of a GE 1.5 MW turbine, which held various yaw offset positions for periods of 1 h at a time (Fleming et al., 2017a). The data from that campaign were used to investigate the accuracy of predictions made by FLORIS (Annoni et al., 2018) and the impact on turbine loads caused by yaw offsets (Damiani et al., 2017). A related campaign is being undertaken at the Scaled Wind Farm Technology facility in Lubbock, Texas. Similar to the National Wind Technology Center study, a rear-facing lidar (in this case the Technical University of Denmark spinner lidar) is used to scan the wake of a V27 experimental turbine. The resulting data are used to examine wake behavior (Herges et al., 2017) and understand loading impacts (White et al., 2018). Finally, a first published field trial at a commercial offshore wind farm is presented in Fleming et al. (2017b). In that study, a single turbine implements a yaw offset control strategy to benefit three downstream turbines.
Still, there is a need for more conclusive field campaigns on the performance of wake steering and the evaluation of the latest models. For this reason, a new field campaign was initiated as a collaboration between the National Renewable Energy Laboratory (NREL) and NextEra Energy Resources. A portion of a commercial wind farm was selected as a test site, and significant additional sensing equipment is being deployed, including a (ground-based) lidar, meteorological (met) tower, and two sodars. Additional nacelle-based lidars are being deployed for the upcoming second phase. Wake steering controls based on the latest version of FLORIS are implemented on two turbines. This paper presents the results of the first phase of this campaign focused on wake steering.
The main contribution of this paper is the initial results and analysis of a land-based wake steering field-test campaign. The paper presents the controller as implemented in the present phase and proposes improvements based on these initial results. The performance of wake steering, in terms of increased energy production, is analyzed and compared with predictions from the FLORIS code. In addition, the wake steering performance is assessed with respect to atmospheric stability, which can be estimated using sensing available on the met mast. Finally, several practical lessons learned are discussed.
The paper is organized as follows. Section 2 provides an overview of the field campaign's layout of turbines and sensors, as well as meteorological conditions. Section 3 discusses the implemented controller. Section 4 describes the data collected in terms of total amount and characteristics. The performance of the controller, specifically in terms of achieving targeted offsets, is reviewed in Sect. 5. Challenges specific to this first phase are described in Sect. 6. Finally, Sect. 7 presents the results.
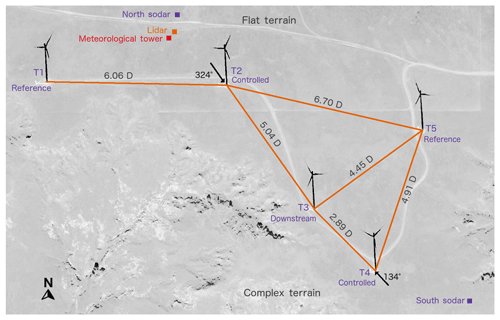
Figure 1Layout of the experimental site. Turbine 2 (T2) and Turbine 4 (T4) have wake steering implemented to benefit Turbine 3 (T3), whereas Turbine 1 (T1) and Turbine 5 (T5) are reference turbines. The position of the installed meteorological equipment is also shown. Finally, the complexity of the terrain to the south and the flat terrain to the north are indicated.
A subsection of a commercial wind farm was selected as the test site for the wake steering campaign. The site was chosen to include a set of turbines for which the main wind directions that generate strong waking conditions would occur relatively frequently and the turbines were close enough for wake steering effects to be discernible. The selected wind farm subsection is shown in Fig. 1.
Five turbines (Fig. 1) are located in one corner of the farm. Note that there are no turbines to the north or south, making these wind directions effectively free stream. The five turbines are relatively closely spaced, especially the three turbines labeled T2, T3, and T4. T2 and T4 were controlled turbines, and T3 was selected as the downstream turbine to be evaluated based on the wake impacts of T2 and T4. The wind directions at which T2 (324∘) and T4 (134∘) directly wake T3 are indicated in Fig. 1. T1 and T5 serve as reference turbines that are uncontrolled and unaffected by the control turbines during wind conditions under which controls would be applied. Figure 2 illustrates the directional conventions for steering applied to the T4 and T3 turbine pair.
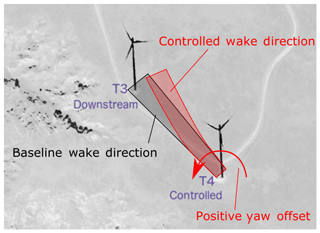
Figure 2Illustration of wake steering showing that a positive yaw offset is meant to indicate a counterclockwise rotation of the controlled turbine.
The terrain of the site is also illustrated in Fig. 1. Generally, the terrain to the north is flat, whereas the terrain to the south is complex (some escarpments can be seen in the southwest in Fig. 1, and these extend to the south of T4). The campaign is divided into the “north” campaign, wherein flows from the north arrive over flat terrain and T2 is the controlled turbine, and the “south” campaign, wherein flows from the south arrive over complex terrain and are expected to be more turbulent.
The locations of the meteorological equipment are indicated in Fig. 1. Based on the simpler terrain and overall wind rose, the equipment is placed to prioritize the north campaign. A Leosphere Windcube v2 profiling lidar (shown in Fig. 1) provides profiles of wind speed and wind direction calculated nominally every second but averaged to 1 min intervals. This lidar (similar to that used in Lundquist et al., 2017) samples line-of-sight velocities in four cardinal directions along a nominally 28∘ azimuth from vertical, followed by a fifth vertically pointed beam. Range gates were centered every 20 m from 40 m up to 180 m. The sodars used in the campaign are Vaisala Triton Wind Profilers. The sodars provide measurements of wind speed and wind direction every 20 m up to 200 m.
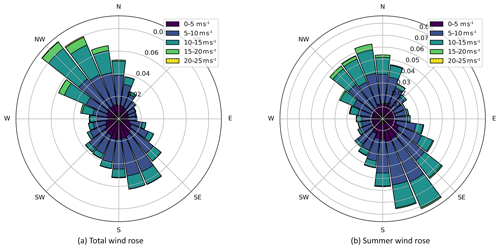
Figure 3Total wind rose for the site and for the particular months encompassing the test based on data collected from https://www.nrel.gov/grid/wind-toolkit.html (last access: 1 May 2019).
Phase 1 of the field campaign uses an initial deployment of the wake steering controller and initial collection of data over the summer of 2018 (from 4 May through 11 July 2018). The wind resource is seasonal: in the summer, southern winds are more probable than northern winds. Figure 3 shows two wind roses for the site, for which data were obtained using the NREL Wind Integration National Dataset tool kit at 100 m of height. Figure 3a shows the annual wind rose, with winds coming dominantly from the north-northwest and south-southeast. Figure 3b shows the expected wind rose for the months during which the campaign was run with more frequent south-southeasterly winds.
Controllers were implemented and running on both T2 and T4. Because the south-southeasterly winds are more prominent in this season, phase 1 focuses on the south campaign as most of the collected data correspond to this direction. The final study will consider the north experiment as well. Because of this focus on the south campaign, the most relevant components in Fig. 1 are T4 (controlled turbine), T3 (downstream turbine), and the south sodar to measure inflow.
The controller implemented onto T4 was designed by optimizing a FLORIS model of the site based on wind direction and wind speed. This resulted in a lookup table, which provides a desired yaw offset for T4 as a function of wind speed and direction. Figure 4 shows this target offset function as a function of wind direction for several wind speeds. The magenta lines indicate the approximate boundary of control and will be reused in upcoming figures to distinguish controlled and uncontrolled wind directions. The offset is largest around the peak wake loss direction near 134∘ and decreases as the wind rotates southerly.
These offset tables were constrained to be below the load impact limitations determined by Damiani et al. (2017). A safe load envelope was determined to be yaw offset angles no larger than 20∘ during wind speeds of 12 m s−1 or less. Finally, offsets were restricted to the counterclockwise direction with respect to the wind (when viewed from above).
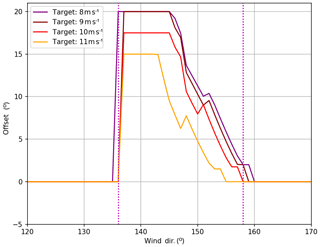
Figure 4Target offset for 8, 9, 10 and 11 m s−1. The red line indicates the target offset by wind direction. The magenta vertical lines indicate the approximate boundaries of the experiment (these vary slightly by wind speed, but the overall shape is the same).
The yaw controllers of the controlled turbines were then modified to implement this yaw offset strategy. Specifically, the nacelle vane signal fed into the controller was modified by the specified yaw offset amount in the lookup table to induce the yaw controller to track an offset. An external wake steering controller was implemented to determine the offset to apply at a given moment. The specific setup is shown in Fig. 5.
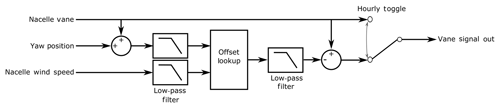
Figure 5Block diagram of wake steering controller implementation. Inputs are provided by a typical turbine sensor, and the output is a modified vane signal to supply the turbine yaw controller for wake steering. Note that this output is toggled on–off hourly. All low-pass filters have a 30 s time constant.
The controller in Fig. 5 computes a wind speed and wind direction from sensors available on each turbine. It then filters both of these signals to remove high-frequency changes. The signals are fed into a lookup table, which is also filtered, and then the modified offset vane signal is sent to the turbine yaw controller.
The offset function is toggled on and off every hour, as indicated in the diagram. This toggling enables the performance of the wake steering controller to be compared to a baseline control dataset that includes a similar composition of wind speeds. The decision to toggle every hour was a balance between accounting for the slowness of most yaw controllers and the variation of wind conditions. The optimal toggling period should be studied in more detail in the future to optimize the usefulness of the data collected.
The phase 1 campaign lasted for approximately 3 months, during which the wake steering offset controller on T4 was toggled on and off hourly. This section describes the inflow conditions during this period.
The inflow conditions are described from the south sodar data. Wind speed and wind direction are computed by a weighted average of the sodar measurements at heights that are within the rotor area of the turbine similar to the rotor-equivalent wind speed (Wagner et al., 2014). Turbulence intensity (TI) is estimated at hub height by the sodar as the 10 min standard deviation of the wind speed divided by the mean wind speed. Finally, stability is quantified via the Obukhov lengths (Stull, 2012). For this case the Obukhov length L is computed via
where K is the von Kármán constant assumed to be 0.4, u∗ is the frictional velocity, g is gravity, θv is virtual potential temperature calculated with the met tower pressure at 2.5 m, and u, v, and w are meteorological coordinates of wind speed components in the west–east, south–north, and vertical planes; the ′ indicates perturbations. Fluxes were calculated using a Reynolds decomposition based on a 30 min average. Using the classification scheme of Wharton and Lundquist (2012), the data were divided into stable, neutral, and unstable conditions. This division is simplified here so that “stable” is defined as m and all other data are categorized as “not stable.”
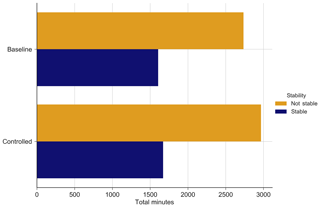
The total amount of data collected is summarized in Fig. 6. The amount of data collected between the “baseline” set, i.e., controller off, and “controlled,” i.e., controller on, is comparable. The data are broken into stable and unstable atmospheric conditions to show that toggling ensures that both sets are similarly composed of atmospheric conditions.
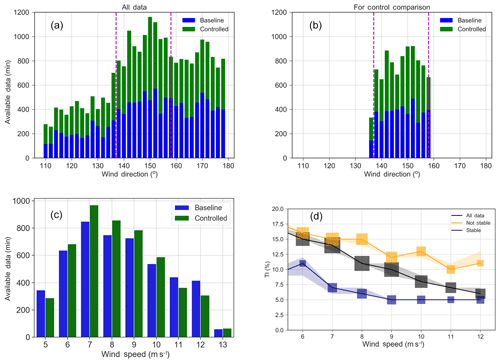
Figure 7Atmospheric conditions observed by the sodar at hub height over the duration of the test campaign.
Atmospheric conditions are described in Fig. 7. In Fig. 7a, the wind directions observed over the course of the campaign (as measured by the south sodar at hub height) are illustrated. If data are restricted to points occurring in the range in which the experimental controller is active (in terms of wind speed and direction) and further limited by the removal of fault-coded data or faulty sensing, the data are reduced to Fig. 7b. The distribution of wind speeds making up Fig. 7b are then shown in Fig. 7c. Finally, Fig. 7d illustrates the recorded TI within the dataset remaining in Fig. 7b. The box sizes in Fig. 7d indicate the amount of data, and the data are subdivided into stable and unstable categories to show that lower wind speeds are more likely to be higher-turbulence, unstable conditions, whereas higher wind speeds tend to be low-turbulence stable conditions. The black line in Fig. 7d will be used to describe the typical TI in the FLORIS model and will be discussed again later.
We first analyze the phase 1 data by considering the performance of the controller in terms of its ability to produce a specific offset by wind speed and wind direction. The exact function of the turbine yaw controller is not known. Therefore, it was difficult to know in advance how effective the method shown in Fig. 5 would be in delivering the desired offsets.
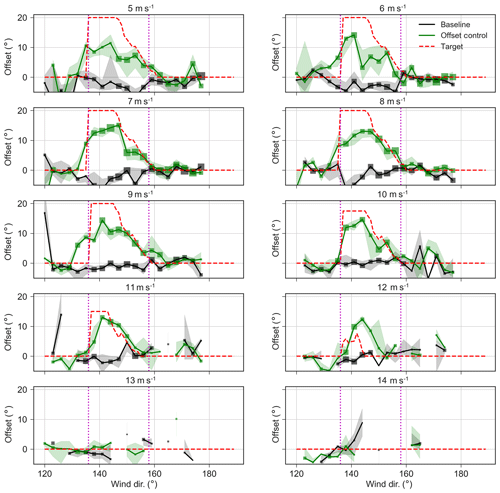
Figure 8Comparison of observed yaw offset (green line) versus target (dashed red line) segregated by wind speeds. Note that the achieved offset is computed as the difference between the sodar-measured wind direction and the turbine nacelle heading. Points indicate median offset, with box size indicating the number of points in a bin and bands indicating the 95 % confidence interval of the median.
Figure 8 assesses the performance of this offset controller. Binned by wind speed, the figure shows the median maintained offset. The offset here is computed by comparing the nacelle position of T4 with the measurement of wind direction recorded by the south sodar. Generally, the offsets are achieved reasonably well; however, there is a tendency toward undershoot. The undershoot could be an artifact of temporal averaging over periods with and without offset, which biases computed offsets toward zero. However, we suspect that the undershoot is actually occurring because of the fact that the actual controller is tracking an offset that is zero for most directions, except for a small band about the main waking direction. As the wind speed and direction drift in and out of controlled areas, the averaging effect biases the offset toward zero. This bias could be accounted for in future controller design.
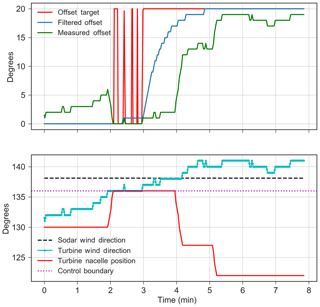
Figure 9Time series data of T4 operation showing the sources of lag in yaw offset control. The figure shows that following the wind direction entering the range at which a 20∘ offset would be optimal at the 2 min mark, the offset is not actually achieved until 3 min later.
In addition to a steady bias toward smaller-than-targeted offsets, we also noticed a dynamic issue in the controller design. The dynamic design of wind farm controllers is a field of active research (Bossanyi, 2018). In the initial design phase, it was assumed that, to avoid excessive yawing behaviors, we should low-pass filter the wind speed and wind direction inputs to the lookup table, as well as the resultant offset sent to the yaw controller. We did not account for the fact that the yaw controller itself acts as a lag filter between changes in wind direction and changes in nacelle yaw position, so the yaw offset control system as a whole is probably too slow and a general tendency toward overlagging changes in wind direction was observed. This is illustrated in Fig. 9. At approximately 2 min, the wind direction crosses into the region in which a 20∘ offset would be dictated by the static optimal lookup table. The low-pass filtering, however, causes the offset target to lag until the third minute to reach 20∘. Then, the filtering of the offset achieves 20∘ around the fourth minute. Further, the turbine is observed to begin yawing around the fourth minute and completes this action in the fifth minute, 3 min after the offset could have been optimally applied. Some lag is unavoidable and potentially desirable to avoid adding too much additional yaw activity to the turbine, but based on this result, the controllers used in the upcoming phase 2 will be designed dynamically and the filter constants adjusted to account for this.
This phase 1 campaign revealed several challenges that could inform future campaigns, including our future phases. Despite these challenges, the wake steering controller did produce the desired result of increasing power at the downstream turbine.
A first set of challenges corresponds to the site conditions for the south campaign. The topography is complex, but the version of FLORIS used in the design and analysis has no terrain-modeling capabilities. This mismatch between the modeling assumptions and reality introduces a degree of uncertainty. Second, T4 and T3 are spaced such that T3 is in the near-wake region of T4. The version of FLORIS used does not contain a well-tuned near-wake model. Finally, as shown in Fig. 6, the collected data are only about one-third composed of stable atmospheric conditions because of the summer season and longer days. Stable, low-turbulence conditions would be more favorable to wake steering and may occur more frequently in the winter season.
A second set of challenges arises from more practical considerations. Specifically, the only sensor that could be used for the south experiment to measure the inflow is the south sodar, as it is the only one to the south of T4. The south sodar, in comparison to other instruments, was shown to measure the inflow well; however, it delivers data only once every 10 min, and this frequency is too coarse for the data analysis because 10 min will include a diverse mix of wind directions and offsets. The turbine data are delivered at a frequency of 1 Hz, and through trial and error, a compromise of down-sampling the turbine data to 1 min periods while up-sampling the sodar data was selected (this up-sampling is done through a “zero-order hold”, wherein the data for each minute bin are assigned the 10 min average). However, in the upcoming north campaign, more frequent data are available from the lidar and can be used.
Finally, the controller design, wherein we influence the yaw controller without fully understanding its behavior, is a major challenge. If the yaw controller could be directly modified, the delays shown in Fig. 9 could be reduced and performance improved.
The first step in performing the analysis was selecting a reference for comparing the power of T3 and T4. In previous work, e.g., Fleming et al. (2017b), a reference uncontrolled turbine was preferred as it would provide a reference power that includes the effects not only of wind speed, but also shear, veer, and TI. For this reason, both T1 and T5 were considered, but a significant amount of noise and noncorrelation was observed, likely because both turbines are far downstream from T4. Ideally, the reference would be parallel to the upstream turbine on a line perpendicular to the controlled wind directions. In addition, the complex terrain varies from T1 to T5.
For this reason, a synthetic reference turbine power was used based on the measurements of the south sodar. The wind speeds at heights corresponding to the turbine rotor were collected and applied to a weighted average, called Usodar, wherein the weights were proportional to the sector of rotor area the heights correspond with, similar to a rotor-effective wind speed calculation (Wagner et al., 2014). The hypothetical power of a reference turbine could then be computed using
where Cp is derived from the Cp lookup table included in FLORIS, ρ is the average observed density, and A is the rotor area. This estimated sodar power was then compared with the measured power of T4 when the turbine is not intentionally operating in the offset condition (Fig. 10). The plot shows that correspondence is very close except for near rated.
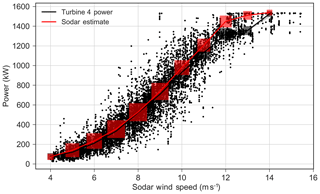
Figure 10Sodar available power fit. The data from T4 are shown in black and the sodar estimate is shown in red. The red boxes refer to the wind speed bins and the size refers to the amount of data in each bin.
To analyze the effect of the wake steering implementation on the control and downstream turbine, the following method of analysis is used. First, the data are limited to include only periods in which both turbines were operating normally and the quality of the sodar estimate was above a certain threshold according to quality flags reported by the sodar at each range. Next, all the data, including the power of T3 and the sodar reference power, are binned into wind direction bins every 2∘ (with 1∘ of overlap between adjacent bins as this was found useful in clarifying trends in the available data) and according to whether the wake steering controller was toggled on (controlled) or off (baseline).
Then for each bin, an energy ratio is computed, which involves a weighted summation of all the power measurements PTest of the test turbine (the determination of the weights w will be detailed later), i.e., T3, and the reference turbine, i.e., sodar estimate PRef, and then a ratio of the two.
Note that this method is different from a power ratio method in which a power ratio is computed for each set of points and then averaged.
It is also different from the slope method used in Fleming et al. (2017b).
where R[…] is the ratio computed through the different methods, PTest and PRef are vectors of all observed powers for the reference and test turbines, is a single-minute average, and N is the total number of points in a given wind direction bin.
The energy ratio (Eq. 4) is used for a few reasons. First, changes in relative energy production are more directly related to changes in revenue. Second, the power ratio is an average of ratios instead of the ratio of averages proposed in the energy ratio (Eq. 5). The power ratio is more sensitive to small changes in power at low wind speeds that do not contribute meaningfully to changes in energy production, which is the ultimate goal. The slope method (Eq. 6) of Fleming et al. (2017b) was able to achieve a weighting of higher wind speeds through slope fitting. However, the energy ratio was finally thought to be more directly related to annual energy production, the overall quantity of interest. The energy ratio represents the increase or decrease in energy produced for a specific wind direction bin.
In computing the energy ratio, a wind-speed-based weighting strategy helps to more quickly converge the analysis and reduce changes in energy ratios due to variations in the compositions of wind speeds for the two controllers within each wind direction bin with respect to differences due to changes in controller. The main idea is that for each wind direction, the power values collected are binned according to wind speed (as measured by the sodar) and the total energy for the baseline and controlled cases is the weighted sum of the powers; the weight is the number of points the other control setting has in this wind speed bin out of the total. For example, if there are 10 samples of baseline taken at 13 m s−1 and 5 of controlled, the baseline points are weighted by 1∕3 and the controlled by 2∕3, so the final energy ratios to be compared are more approximately even in terms of the wind speed distributions represented. If the bins are perfectly balanced, there are an equivalent number of baseline and controlled points at each wind speed, and the weights have no effect.
In addition to computing a single energy ratio for each bin, the process is bootstrapped, whereby the data are randomly sampled with replacement and the energy ratio recomputed 1000 times or more depending on the amount of data. The results of these bootstrap iterations are then used to compute 95 % confidence intervals, and these are indicated in the plots of the energy ratio as semi-transparent bands.
The method of computing energy ratios is now included within the open-source FLORIS model (https://floris.readthedocs.io, last access: 1 May 2019).
Note that all wind speeds are used in this calculation, including those (greater than 12 m s−1) in which the 0∘ offset is actually targeted, even in the controller on mode. With the 10 min sodar rate and the lag of the controller, it is difficult to draw an exact line where the controller stops impacting the individual turbine yaw controller. Including all wind speeds also corresponds to the final change in energy.
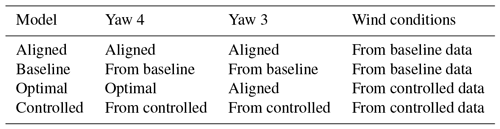
The energy ratio calculation is repeated on several differently defined FLORIS models of the site to provide a point of comparison. An “aligned” case simulates every observed wind speed and direction in the baseline field data with all turbines perfectly aligned to the flow, while a baseline case uses the actual small offsets observed. An “optimal” case simulates all the wind speeds and directions in the controlled field data using the exact offset requested by the control strategy, while the controlled case applies the actual achieved offset. These four settings are summarized in Table 1. For each of the FLORIS models and for each 1 min wind speed and direction observed in the field, a matching FLORIS simulation was run, the power of T3 and T4 tabulated, and the energy ratio computed. When considering gains in energy, FLORIS optimal gain refers to the change from aligned to optimal, whereas FLORIS controlled gain refers to the change from baseline to controlled.
Table 1FLORIS model definitions for comparison. The columns yaw 4 and yaw 3 determine what sets the yaw angle for each turbine (aligned is always 0∘), with optimal being the true optimal; “from baseline” means applying the observed yaw angles from the baseline data of the field campaign. Wind conditions are similarly defined.
The energy ratios can be computed from these FLORIS models. The comparison of the aligned and optimal case should present an upper bound on performance if exact offsets and alignments held, whereas the baseline and controlled cases show what we expect from this dataset.
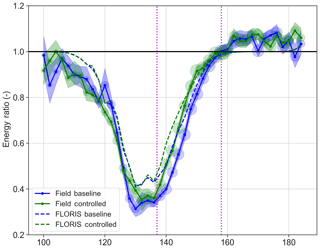
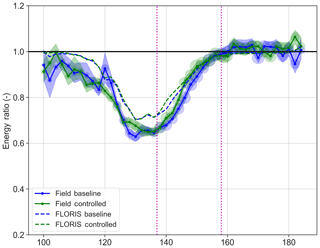
Figure 11Energy ratio for T3 for field data and the baseline and controlled FLORIS cases (see Table 1). An energy ratio of 0.5 corresponds to a production of 50 % of the total expected based on the measured inflow without considering wakes. The vertical magenta lines indicate the region where control is applied and a difference between the baseline and controlled is expected. The size of the circles at each point indicates the number of points in the bin, while the bands indicate 95 % confidence as computed by bootstrapping.
7.1 Turbine 3 analysis
Figure 11 shows the energy ratios by wind direction for T3. The wake loss is deeper than FLORIS expects (T3 is producing less than 40 % of the energy of the reference at nadir); however, as mentioned, this is a difficulty of current near-wake models and the subject of active research. Still, the gain in energy production in the wind direction for which the controller is active is observed. Note that as described earlier, to clarify trends, the wind direction bins are every 2∘ but are 3∘ wide (overlapping with adjacent) to increase the number of points available per bin.
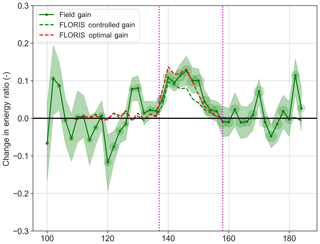
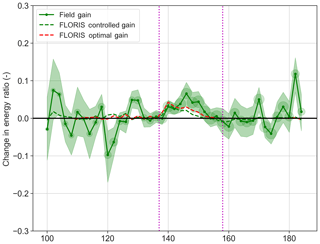
Figure 12Change in the energy ratio of T3 from field data. Expectations from FLORIS using the actually achieved controlled offsets (controlled − baseline) and optimal (optimal − aligned) are shown to indicate comparison with expectations given control values and what is optimally expected.
The difference between the baseline and controlled cases for both the field data and FLORIS quantifies the impact of yaw control on power production (Fig. 12). In the 10∘ sector between 140 and 150∘ the average gain in energy is 14.6 %. Compared to FLORIS predictions, the field results compare favorably to the estimations from FLORIS. The data outside of the control bands, while noisy, indicate an average around 0, underlining the significance of the nonzero apparent average in the control region.
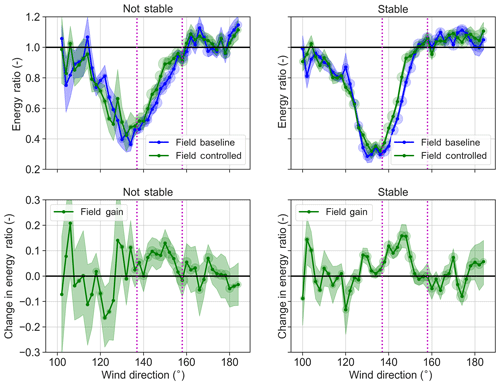
Figure 13 segregates stable conditions from unstable conditions and repeats the analysis of Figs. 11 and 12. The gain in stable conditions is more consistently realized (as indicated by the bands) and the peak gain is higher than in unstable conditions. This distinct improvement in stable conditions could be because wake steering is more effective in stable conditions. Additionally, in stable conditions, atmospheric inflow is more homogeneous and therefore easier to measure. Upcoming winter measurements from the north for phase 2 will consist of more stable measurements due to the longer nights and may shed more light on the role of atmospheric stability in wake steering.
7.2 Aggregate analysis
Finally, the previously mentioned analysis is repeated, but using the aggregated power of T4 and T3, so that the losses in energy coming from offsetting the yaw of T4 are deducted from the gains made downstream (Fig. 14 shows the energy ratios and Fig. 15 shows the difference between them). The aggregated energy gains appear to be somewhat more than the current version of FLORIS expects (a net gain of 4.1 % over the same 10∘ region from 140 to 150∘), but this could again be connected to difficulty measuring the near wake.
We present the initial results from the first phase of a field campaign evaluating wake steering at a commercial wind farm. For two closely spaced turbines, an approximate 14 % increase in energy was measured on the downstream turbine over a 10∘ sector with a 4 % increase in energy when accounting for losses of the upstream turbine. The gains in energy were compared to predictions made using the FLORIS model used to design the applied controllers. The overall gains were consistent with predictions from FLORIS.
This initial stage of the wake steering campaign identified several areas for improvement in future work, such as aspects of dynamic controller design, time filtering, and uncertainty quantification. Difficulties with this particular south campaign, including complex terrain and summer atmospheric conditions, were identified as possible sources of improvement as the campaign moves to northern winter conditions. Additionally, near-wake modeling presented a challenge in accurately modeling the wake losses and therefore may have realized a less-than-optimal controller. Still, the overall gains in energy were in line with prior expectations from FLORIS.
All together, the authors hope that the results presented might therefore represent a baseline for the possibility of gains from wake steering. Better modeling and controls, simpler site conditions, and the exploitation of vortex modeling and larger arrays of turbines all present hopeful avenues for continued improvements. An upcoming companion paper on the second phase of the experiment will review results, including the opportunities for improvement identified in this paper.
Currently, the data are not publicly available; however, if in the future portions of the data become available, this would be through the DOE A2e data portal at https://a2e.energy.gov/about/dap.
All coauthors were involved in writing and editing the paper. The design of the controller and analysis of data were performed by PF, JK, KD, ES, PM, JKL, KF, CB, RM, and PM. The implementation of experiments at the site was done by JR, AS, JvD, HL, JS, MS, BR, CG, and DB.
The authors declare that they have no conflict of interest.
The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government.
Funding provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Wind Energy Technologies Office.
This paper was edited by Sandrine Aubrun and reviewed by two anonymous referees.
Annoni, J., Fleming, P., Scholbrock, A., Roadman, J., Dana, S., Adcock, C., Porte-Agel, F., Raach, S., Haizmann, F., and Schlipf, D.: Analysis of control-oriented wake modeling tools using lidar field results, Wind Energ. Sci., 3, 819–831, https://doi.org/10.5194/wes-3-819-2018, 2018. a, b
Bartl, J., Mühle, F., and Sætran, L.: Wind tunnel study on power output and yaw moments for two yaw-controlled model wind turbines, Wind Energ. Sci., 3, 489–502, https://doi.org/10.5194/wes-3-489-2018, 2018. a
Bastankhah, M. and Porté-Agel, F.: A new analytical model for wind-turbine wakes, Renew. Energ., 70, 116–123, 2014. a
Bastankhah, M. and Porté-Agel, F.: Experimental and theoretical study of wind turbine wakes in yawed conditions, J. Fluid Mech., 806, 506–541, 2016. a
Bossanyi, E.: Combining induction control and wake steering for wind farm energy and fatigue loads optimisation, J. Phys. Conf. Ser., 1037, 032011, https://doi.org/10.1088/1742-6596/1037/3/032011, 2018. a
Dahlberg, J. and Medici, D.: Potential improvement of wind turbine array efficiency by active wake control (AWC), in: Proc European Wind Energy Conference, 65–84, 2003. a
Damiani, R., Dana, S., Annoni, J., Fleming, P., Roadman, J., van Dam, J., and Dykes, K.: Assessment of wind turbine component loads under yaw-offset conditions, Wind Energ. Sci., 3, 173–189, https://doi.org/10.5194/wes-3-173-2018, 2018. a, b
Fleming, P., Gebraad, P. M., Lee, S., Wingerden, J.-W., Johnson, K., Churchfield, M., Michalakes, J., Spalart, P., and Moriarty, P.: Simulation comparison of wake mitigation control strategies for a two-turbine case, Wind Energy, 18, 2135–2143, 2015. a
Fleming, P., Annoni, J., Scholbrock, A., Quon, E., Dana, S., Schreck, S., Raach, S., Haizmann, F., and Schlipf, D.: Full-scale field test of wake steering, J. Phys. Conf. Ser., 854, 012013, https://doi.org/10.1088/1742-6596/854/1/012013, 2017a. a
Fleming, P., Annoni, J., Shah, J. J., Wang, L., Ananthan, S., Zhang, Z., Hutchings, K., Wang, P., Chen, W., and Chen, L.: Field test of wake steering at an offshore wind farm, Wind Energ. Sci., 2, 229-239, https://doi.org/10.5194/wes-2-229-2017, 2017b. a, b, c, d
Gebraad, P., Teeuwisse, F., Wingerden, J., Fleming, P. A., Ruben, S., Marden, J., and Pao, L.: Wind plant power optimization through yaw control using a parametric model for wake effects – a CFD simulation study, Wind Energy, 19, 95–114, 2016. a
Herges, T., Maniaci, D. C., Naughton, B. T., Mikkelsen, T., and Sjöholm, M.: High resolution wind turbine wake measurements with a scanning lidar, J. Phys. Conf. Ser., 854, 012021, https://doi.org/10.1088/1742-6596/854/1/012021, 2017. a
Howland, M. F., Bossuyt, J., Martinez-Tossas, L. A., Meyers, J., and Meneveau, C.: Wake structure in actuator disk models of wind turbines in yaw under uniform inflow conditions, J. Renew. Sustain. Energ., 8, 043301, https://doi.org/10.1063/1.4955091, 2016. a
Jensen, N. O.: A note on wind generator interaction, Tech. Rep. Risø-M-2411, Risø National Laboratory, 1984. a, b
Jiménez, Á., Crespo, A., and Migoya, E.: Application of a LES technique to characterize the wake deflection of a wind turbine in yaw, Wind Energy, 13, 559–572, 2010. a, b
Lundquist, J. K., Wilczak, J. M., Ashton, R., Bianco, L., Brewer, W. A., Choukulkar, A., Clifton, A., Debnath, M., Delgado, R., Friedrich, K., Gunter, S., Hamidi, A., Iungo, G. V., Kaushik, A., Kosović, B., Langan, P., Lass, A., Lavin, E., Lee, J. C.-Y., McCaffrey, K. L., Newsom, R. K., Noone, D. C., Oncley, S. P., Quelet, P. T., Sandberg, S. P., Schroeder, J. L., Shaw, W. J., Sparling, L., Martin, C. S., Pe, A. S., Strobach, E., Tay, K., Vanderwende, B. J., Weickmann, A., Wolfe, D., and Worsnop, R.: Assessing State-of-the-Art Capabilities for Probing the Atmospheric Boundary Layer: The XPIA Field Campaign, B. Am. Meteorol. Soc., 98, 289–314, https://doi.org/10.1175/BAMS-D-15-00151.1, 2017. a
Martínez-Tossas, L. A., Annoni, J., Fleming, P. A., and Churchfield, M. J.: The aerodynamics of the curled wake: a simplified model in view of flow control, Wind Energ. Sci., 4, 127–138, https://doi.org/10.5194/wes-4-127-2019, 2019. a
Medici, D. and Alfredsson, P.: Measurements on a wind turbine wake: 3D effects and bluff body vortex shedding, Wind Energy, 9, 219–236, 2006. a
Niayifar, A. and Porté-Agel, F.: A new analytical model for wind farm power prediction, J. Phys. Conf. Ser., 625, 012039, https://doi.org/10.1088/1742-6596/625/1/012039, 2015. a
NREL: FLORIS, Version 1.0.0, available at: https://github.com/NREL/floris, last access: 1 May 2019. a
Park, J., Kwon, S.-D., and Law, K. H.: A data-driven approach for cooperative wind farm control, in: American Control Conference (ACC), IEEE 2016, 525–530, 2016. a
Schottler, J., Mühle, F., Bartl, J., Peinke, J., Adaramola, M. S., Sætran, L., and Hölling, M.: Comparative study on the wake deflection behind yawed wind turbine models, J. Phys. Conf. Ser., 854, 012032, https://doi.org/10.1088/1742-6596/854/1/012032, 2017. a
Stull, R. B.: An introduction to boundary layer meteorology, vol. 13, Springer Science & Business Media, 2012. a
Vollmer, L., Steinfeld, G., Heinemann, D., and Kühn, M.: Estimating the wake deflection downstream of a wind turbine in different atmospheric stabilities: an LES study, Wind Energ. Sci., 1, 129–141, https://doi.org/10.5194/wes-1-129-2016, 2016. a
Wagenaar, J., Machielse, L., and Schepers, J.: Controlling wind in ECN's scaled wind farm, Proc. Europe Premier Wind Energy Event, Copenhage, Denmark, 16–19 April 2012, ECN, 685–694, 2012. a, b
Wagner, R., Cañadillas, B., Clifton, A., Feeney, S., Nygaard, N., Poodt, M., St Martin, C., Tüxen, E., and Wagenaar, J.: Rotor equivalent wind speed for power curve measurement–comparative exercise for IEA Wind Annex 32, J. Phys. Conf. Ser., 524, 012108, https://doi.org/10.1088/1742-6596/524/1/012108, 2014. a, b
Wharton, S. and Lundquist, J. K.: Atmospheric stability affects wind turbine power collection, Environ. Res. Lett., 7, 014005, https://doi.org/10.1088/1748-9326/7/1/014005, 2012. a
White, J., Ennis, B., and Herges, T. G.: Estimation of Rotor Loads Due to Wake Steering, in: 2018 Wind Energy Symposium, Kissimmee, Florida, 8–12 January 2018, https://doi.org/10.2514/6.2018-1730, 2018. a