Detection of wakes in the inflow of turbines using nacelle lidars

Nacelle-mounted lidar systems offer the possibility of remotely sensing the inflow of wind turbines. Due to the limitation of line-of-sight measurements and the limited number of focus positions, assumptions are necessary to derive useful inflow characteristics. Typically, horizontally homogeneous inflow is assumed which is well satisfied in flat, homogeneous terrain and over sufficiently large time averages. However, it is violated if a wake impinges the field of view of one of the beams. In such situations, the turbine yaw misalignment measurements show large biases which require the detection and correction of these observations. Here, a detection algorithm is proposed based on the spectral broadening of the Doppler spectrum due to turbulence within the probe volume. The small-scale turbulence generated within wake flows will typically lead to a significantly larger broadening than in the ambient flow. Thus, by comparing the spectral widths at several measurement locations, situations where a wake is impinging one or more measurement locations can be identified. The correction method is based on an empirical relationship between the difference in turbulence levels at distinct beams and the difference in wind direction derived from the lidar and the real wind direction. The performance of the algorithm is evaluated in a field experiment identifying all wake situations and, thus, correcting the lidar derived wind direction.

1 Introduction

Modern wind turbines usually follow an upwind turbine design in which the rotor is installed upstream of the tower. This design requires an active yaw angle control which traditionally uses a nacelle-mounted sonic anemometer or wind vane misalignment measurements to align the turbine with the wind. The yaw motor actuation is slow to avoid excessive wear on its components, and temporary yaw misalignment is unavoidable (Burton et al., 2011). On the other hand, a systematic error in yaw tracking leads to production losses and should be prevented.

One source of yaw tracking error stems from the misalignment measurements made by the nacelle sonic anemometer or wind vane, which are heavily disturbed by the flow around the rotor blades and the nacelle. These yaw sensors can be calibrated against undisturbed reference wind direction sensors, for example mast-mounted sonic anemometers and wind vanes or vertically profiling lidars. However, differences in inflow and site conditions between the calibration site and the actual installation site of the turbine are not reflected in this calibration and might introduce biases in the measurements. A method to detect and correct the degradation of the sensors over time is presented in Mittelmeier and Kühn (2018). Additionally, field experiments showed that wakes from neighbouring turbines can lead to yaw offsets from the dominant wind direction for downstream turbines (Schepers, 2009; McKay et al., 2013).

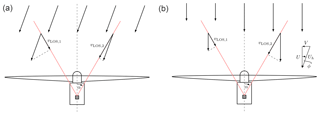
Figure 1 Illustration of a two-beam nacelle lidar mounted on a wind turbine to measure yaw misalignment. Misaligned horizontally homogeneous flow will affect the LOS measurements at the two focus positions (a). A wake in the field of view on one of the beams will affect the LOS measurement in a similar way as a misaligned flow (b). From lidar measurements these two situations cannot be distinguished. The variables are introduced in Sect. 2.1.

Several alternative sensors have been proposed to sense yaw misalignment. In Pedersen et al. (2015) the use of spinner anemometry is suggested to overcome the flow distortions from blades and the nacelle. Three one-dimensional sonic anemometers were mounted at the spinner to measure horizontal wind speed, yaw misalignment and flow inclination. Calibration of the sensor is necessary to remove measurement biases (Demurtas and Janssen, 2016).

A wind state observer for vertical and horizontal shear, yaw misalignment and flow inclination based on flap- and edgewise blade bending moment measurements was formulated and tested through simulations in Bertelè et al. (2017) and validated on a scaled experimental turbine in Bertelè et al. (2018). In Bottasso et al. (2018) a similar observer using flapwise blade bending moments was developed to estimate the average wind speed over four azimuthal sectors of the rotor plane. By comparing upper with lower and left with right sector, vertical shear and impinging wakes from upstream turbines could be detected. For the detection of wakes, the derived sector-wise mean wind speed and turbulence intensity were used.

Nacelle-mounted light detection and ranging (lidar) devices have also been suggested to estimate yaw misalignment (Scholbrock et al., 2015; Fleming et al., 2014). Due to their remote sensing capabilities, it is possible to measure the inflow in front of the turbine. Measurements at a close distance from the rotor are affected by the induction of the turbine, but the severe influences of blades and nacelle behind the rotor can be avoided. However, measuring only the line-of-sight (LOS) component along the laser beam requires the lidar systems to probe the wind field at several position over the rotor plane and to make assumptions of the incoming flow field to derive the yaw misalignment of the turbine, leading to limitations. Thus, nacelle lidars are designed to steer the laser light towards several focus positions. The most simple setup is a two-beam system which scans two horizontal positions at the hub height of the turbine; see Fig. 1.

To derive the yaw misalignment from nacelle lidar measurements two common assumptions are made:

1. no vertical wind vector component

2. horizontally homogeneous flow.

In the case of a horizontally scanning lidar, the measured vertical component will always be very small since only the LOS can be measured. Further, the horizontally homogeneous flow assumption is well satisfied if the terrain is flat and homogeneous and if appropriate averages over time (commonly 1 to 10 min averages) are taken. Note that by changing the second assumption to a perfect yaw alignment, the measurement of the lidar system can be interpreted as horizontal shear. This can pose a problem if the lidar is used for yaw alignment and cyclic pitch control (Schlipf, 2015).

The assumption of horizontal homogeneity is violated if a wake from an upstream turbine is impinging the field of view of one of the beams. Such a situation is illustrated in the right panel of Fig. 1. The left half of the rotor is exposed to a lower wind speed due to the wake, and thus the measurement at the left LOS, $v_{{\mathrm{LOS}}_{\mathrm{1}}}$, is reduced. This is similar to a reduction of one of the LOS speeds due to misaligned flow and cannot be distinguish from lidar measurements; see left illustration in Fig. 1. Thus, an impinging wake in the field of view of one of the beams will lead to a yaw misalignment measurement even though the flow is aligned. If the lidar should supply yaw misalignment measurements to the yaw controller, these situations need to be identified and, if possible, the influence of the wake needs to be corrected for.

In general, scanning lidar systems, where the laser follows a trajectory rather than probes' discrete points, are able to measure large-scale flow phenomena due to their high spatial and temporal resolution. The first field experiment of measuring wakes behind turbines by a scanning continuous-wave (cw) lidar was conducted by Bingöl et al. (2010) and Trujillo et al. (2011). A cw lidar was mounted on the nacelle of a turbine looking downstream, and the derived flow information was sufficient to identify and characterize the meandering of the wake. More recently, a nacelle-mounted cw lidar with a fast scanning head was used to provide a detailed image of wake behind a turbine and track its movement under different atmospheric conditions (Herges et al., 2017). Long-range pulsed lidars positioned on the ground (Iungo et al., 2013; Smalikho et al., 2013; Bodini et al., 2017) or in offshore wind farms (Krishnamurthy et al., 2017) have also been used to measure wakes. The advantage of pulsed systems is their increased range (of several kilometres) compared to cw systems which allow the visualization of the wakes of multiple turbines in a wind farm.

However, the limited amount of information gathered by commercially available nacelle lidars makes the detection and characterization of wakes challenging. Currently, commercially available systems include Windar Photonics' two- and four-beam cw lidars with fixed focus distance, Leosphere's four-beam pulsed lidar with multiple focus distances and ZX Lidars' cw lidar with 50 focus points distributed on a cone at variable focus distances¹.

In this study Windar Photonics' two-beam nacelle lidar will be used to investigate the effect of wakes on the turbine yaw misalignment measurements. The aim is to detect half-wake situations that lead to biased misalignment measurements and to correct the measurements so that they can be used to perform turbine yaw alignment. First, we will propose an algorithm that utilizes the spectral broadening of Doppler peaks from small-scale turbulence to detect wakes in the turbine inflow (Sect. 2). We will then present the results of the algorithm (Sect. 4) gathered during a field experiment described in Sect. 3. Finally, an empirical relationship between the spectral width measurements and the difference in wind direction between lidar and a mast-mounted sonic anemometer is used to correct the erroneous misalignment measurements.

Results of proposed wake detection algorithm have already been presented in Held et al. (2018). In this study measurements from a commercial wind farm have been used and the detection performance of one lidar mounted on a turbine with wakes originating from several surrounding turbines was assessed. The turbine spacing ranged from three to seven rotor diameters. It was shown that the algorithm was able to detect the wakes from all surrounding turbines. Note that the correction method presented in this study was not applied, because a reference wind direction sensor was not available.

The results of the wake detection algorithm not only can be applied to detect erroneous yaw misalignment measurements but can also be applied to wind farm control, e.g. for wake steering. Wake-steering wind farm control is also possible without the use of lidars, but Quick et al. (2017) showed that if uncertainty in the estimation of wind direction is considered, the benefits of wind farm control vanish compared to single turbine optimization. Nacelle lidars offer the possibility to reduce the uncertainty of the yaw misalignment uncertainty and help improve the performance of a wake steering wind farm controller. In Raach et al. (2017) backwards-facing nacelle lidars were used to track the wake behind a turbine, which was subsequently used as input for a wake-steering wind farm controller. A similar approach is possible with forward-facing nacelle lidars considered here. The lidar can provide information on whether a downstream turbine is affected by a wake and if an upstream turbine needs to be misaligned to deflect the wake.

2 Methodology

2.1 Measurement principles of nacelle lidars

The fluctuating part of a three-dimensional (3-D) wind field can be described by the vector field $\mathit{u}(\mathit{x},t)=(u_{\mathrm{1}},u_{\mathrm{2}},u_{\mathrm{3}})$, where x and t refer to positions in space and time, respectively. Lidar systems can sense wind speed by measuring the Doppler frequency shift of the backscattered laser light from aerosols suspended in the atmosphere. Cw systems emit light focused on a point in space continuously, while pulsed systems transmit parcels of light and measure the backscatter as the light progresses in space. In this study we will focus on cw lidars.

The measurement process of a cw lidar can be represented mathematically as the convolution between the projected LOS component n⋅u and a weighting function φ(s) based on the laser intensity:

$$\begin{array}{}\text{(1)}& v_{\mathrm{LOS}}\left(\mathit{r}\right)=\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}\mathit{\phi }\left(s\right)\mathit{n}\cdot \mathit{u}(s\mathit{n}+\mathit{r})\text{d}s,\end{array}$$

where n is the laser beam unit directional vector, r is the focus position and s is distance from the focus position along the laser line (Mann et al., 2010). The weighting function of a cw lidar can be approximated by (Sonnenschein and Horrigan, 1971)

$$\begin{array}{}\text{(2)}& \mathit{\phi }\left(s\right)={\displaystyle \frac{\mathrm{1}}{\mathit{\pi }}}{\displaystyle \frac{z_{\text{R}}}{z_{\text{R}}^{\mathrm{2}}+s^{\mathrm{2}}}},\end{array}$$

where z_R is the Rayleigh length that characterizes the probe volume of the lidar. It depends on the focus distance squared, i.e. $z_{\text{R}}\propto |\mathit{r}{|}^{\mathrm{2}}$, and can vary between a few centimetres to tens of metres. The probe volume has an attenuating effect on the turbulent fluctuations in u, and variances (and thus turbulence intensities) will be underestimated. The attenuated turbulent fluctuations will cause a broadening of the Doppler spectrum. The Doppler spectrum S(v,r) as function of LOS component wind speed can be defined by

$$\begin{array}{}\text{(3)}& S(v,\mathit{r})=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathit{\phi }\left(s\right)\mathit{\delta }(v-\mathit{n}\cdot \mathit{u}(s\mathit{n}+\mathit{r}\left)\right)\text{d}s,\end{array}$$

where δ(.) is the Dirac delta function. The delta function implies that the Doppler spectrum is an integration (or summation) of the values of φ(s), where $\mathit{n}\cdot \mathit{u}(s\mathit{n}+\mathit{r})=v$. The LOS speed v_LOS, as defined by Eq. (1), is the first statistical moment of S(v,r):

$$\begin{array}{}\text{(4)}& v_{\mathrm{LOS}}\left(\mathit{r}\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}vS(v,\mathit{r})\text{d}v,\end{array}$$

where ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}S(v,\mathit{r})\text{d}v=\mathrm{1}$ is assumed. The second central statistical moment of S(v,r) is the variance and a measure of the width of S(v,r):

$$\begin{array}{}\text{(5)}& {\mathit{\sigma }}_{\mathrm{LOS}}^{\mathrm{2}}\left(\mathit{r}\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(v-v_{\mathrm{LOS}}(\mathit{r}\left){)}^{\mathrm{2}}S\right(v,\mathit{r})\text{d}v.\end{array}$$

Based on the inflow assumption mentioned in Sect. 1, the LOS speed measurements at the two positions of a two-beam lidar can be used to derive the yaw misalignment of the turbine (see also Fig. 1). The following set of equations is used, where the hat notation ( $\widehat{.}$ ) is used to indicate estimations from the lidar:

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }{v}_{{\mathrm{LOS}}_{\mathrm{1}}}=U\cos \mathit{\alpha }-V\sin \mathit{\alpha }\text{(7)}& {\displaystyle }& {\displaystyle }{v}_{{\mathrm{LOS}}_{\mathrm{2}}}=U\cos \mathit{\alpha }+V\sin \mathit{\alpha }\text{(8)}& {\displaystyle }& {\displaystyle }\widehat{U}={\displaystyle \frac{v_{{\mathrm{LOS}}_{\mathrm{2}}}+v_{{\mathrm{LOS}}_{\mathrm{1}}}}{\mathrm{2}\cos \mathit{\alpha }}}\text{(9)}& {\displaystyle }& {\displaystyle }\widehat{V}={\displaystyle \frac{v_{{\mathrm{LOS}}_{\mathrm{2}}}-v_{{\mathrm{LOS}}_{\mathrm{1}}}}{\mathrm{2}\sin \mathit{\alpha }}}\text{(10)}& {\displaystyle }& {\displaystyle }{\widehat{U}}_{\mathrm{h}}=\sqrt{{\widehat{U}}^{\mathrm{2}}+{\widehat{V}}^{\mathrm{2}}}\text{(11)}& {\displaystyle }& {\displaystyle }\widehat{\mathit{\varphi }}={\tan }^{-\mathrm{1}}\left({\displaystyle \frac{\widehat{V}}{\widehat{U}}}\right),\end{array}$$

where U and V are longitudinal and lateral wind speed, respectively, and α is the angle between the shaft axis and the laser beam. In the case of the two-beam lidar by Windar Photonics, $\mathit{\alpha }=\mathrm{30}{}^{\circ }$. Yaw misalignment is defined as the angle the turbine needs to yaw in the clockwise direction (seen from above) to align itself with the flow (see Fig. 1).

An impinging wake in the field of view of one of the beams will lead to a bias in the lidar-estimated quantities (Eqs. 8–11). Here, we will analyse the case, where LOS 1 is affected by a reduction in the streamwise wind speed component due to an upstream wake deficit u_w, i.e. $v_{{\mathrm{LOS}}_{\mathrm{1}}}=(U-u_{\mathrm{w}})\cos \mathit{\alpha }-V\sin \mathit{\alpha }$. The influence of u_w on $\widehat{\mathit{\varphi }}$ and ${\widehat{U}}_{\mathrm{h}}$ for different turbine misalignments ϕ is presented in Fig. 2.

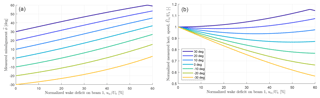
Figure 2 Influence of a streamwise flow speed reduction due to a wake u_w at LOS 1 on the lidar estimates of turbine yaw misalignment $\widehat{\mathit{\varphi }}$ and horizontal wind speed ${\widehat{U}}_{\mathrm{h}}$. The differently coloured lines represent different turbine misalignments ϕ.

It can be seen that an increasing wake deficit imposes a positive bias onto $\widehat{\mathit{\varphi }}$ since $v_{{\mathrm{LOS}}_{\mathrm{1}}}$ is reduced. The kinks that appear for the positive turbine misalignments occur once the wake deficit reduces the LOS 1 component to negative values. However, since the lidar uses a homodyne detection method, only the magnitude, not the sign, of LOS 1 component can be sensed, and the measured misalignment ranges between −60 and 60^∘. The effect of u_w on ${\widehat{U}}_{\mathrm{h}}$ leads to an over- and underestimation of the horizontal wind speed. Again, the negative turbine misalignments are effected more severely than positive misalignments.

2.2 Wake detection algorithm

The wake detection algorithm is based on the following two principles:

1. Within wind turbine wakes turbulence with a smaller length scale than the ambient flow is generated.

2. The small-scale turbulence will lead to a broadening of the Doppler spectrum due to the large probe volume of the lidar system.

The generation of small-scale turbulence has been investigated through simulations, scaled wind tunnel experiments and field tests. The primary aim was to validate mean wake deficit profiles, but some studies also investigated turbulence profiles and applied spectral analysis.

For example, in Troldborg et al. (2007) large eddy flow simulations were conducted with an actuator line model representing the wind turbine. Enhanced levels of small-scale turbulence inside the wake were found. It was also found that the turbulence inside a wake is more isotropic than the ambient flow. Similar results were found in a scaled wind tunnel test. Singh et al. (2014) showed that wind turbines extract energy from mean and large-scale structures while increasing small-scale turbulence. In the near wake, a clear influence of the rotor is visible (e.g spikes at tower and blade frequencies in the turbulence spectra), but in the far-wake these effects merged into a range of amplified small-scale turbulences (Chamorro et al., 2012).

Field experiments using mast anemometry also compared power spectra between wake and ambient flow. In Højstrup (1999) input of energy to high frequencies was observed, which was detectable up to 14.5 rotor diameters behind the turbine. Similar result were obtained in Högström et al. (1988) in which the high-frequency components of the streamwise component increased 4-fold in the wake three rotor diameters behind the turbine. Iungo et al. (2013) analysed wake observations gathered with a pulsed lidar system and also found increased turbulence, but more turbulence was created at the top of the rotor compared to the bottom part.

The effect of spectral broadening of the Doppler spectrum due to turbulence and Doppler spectrum width measurements has been considered in several studies; for an overview see Sathe and Mann (2013). For example, Smalikho (1995) described the broadening process theoretically and proposed a method to measure the dissipation rate of turbulent kinetic energy. Branlard et al. (2013) showed that long time averages of the Doppler spectrum (in this case 10 and 30 min) approach the probability density function of a sonic anemometer and can be used to improve variance measurements. The same method to derive unfiltered variance was used for vertical-profiling lidars (Mann et al., 2010) and nacelle lidars (Peña et al., 2017).

For both properties mentioned in the numbered list at the beginning of this subsection, we will define the LOS-equivalent turbulence intensity, TI_LOS, to characterize the small-scale turbulence contained in the probe volume of the lidar:

$$\begin{array}{}\text{(12)}& {\mathrm{TI}}_{\mathrm{LOS}}\left(\mathit{r}\right)={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{LOS}}\left(\mathit{r}\right)}{v_{\mathrm{LOS}}\left(\mathit{r}\right)}},\end{array}$$

including the difference in TI_LOS between LOS 1 and LOS 2

$$\begin{array}{}\text{(13)}& \mathrm{\Delta }{\mathrm{TI}}_{\mathrm{LOS}}={\mathrm{TI}}_{\mathrm{LOS}}\left({\mathit{r}}_{{\mathrm{LOS}}_{\mathrm{1}}}\right)-{\mathrm{TI}}_{\mathrm{LOS}}\left({\mathit{r}}_{{\mathrm{LOS}}_{\mathrm{2}}}\right),\end{array}$$

where the ${\mathit{r}}_{{\mathrm{LOS}}_{\mathrm{1}}}$ and ${\mathit{r}}_{{\mathrm{LOS}}_{\mathrm{2}}}$ refer to the focus positions of beam 1 and beam 2. The turbulence intensities and their differences will be calculated from 1 min average spectra. Shorted averaging times have also been tried, but the best performance was achieved with 1 min averages. If a beam is exposed to a wake inflow we expect an increased TI_LOS compared to a beam exposed to the ambient flow. Considering turbulence intensities allows the comparison of different wind speed regimes.

The wake detection algorithm is designed to treat the 1 min spectra consecutively and will compare the values of the detection parameters ${\mathrm{TI}}_{\mathrm{LOS}}\left({\mathit{r}}_{{\mathrm{LOS}}_{\mathrm{1}}}\right)$, ${\mathrm{TI}}_{\mathrm{LOS}}\left({\mathit{r}}_{{\mathrm{LOS}}_{\mathrm{2}}}\right)$, ΔTI_LOS and $\widehat{\mathit{\varphi }}$ to their values from ambient, wake-free conditions. A running average of these values is calculated from previous measurements. The running averages aim to represent the values of the detection parameters under ambient, wake-free conditions, and situations in which a wake has been identified will not contribute to the running averages.

Based on threshold values of the detection parameters, the algorithm will then decide whether one or both beams are affected by a wake. For example, if beam 1 is affected by a wake, $v_{{\mathrm{LOS}}_{\mathrm{1}}}$ will be reduced compared to $v_{{\mathrm{LOS}}_{\mathrm{2}}}$ even though the misalignment of the turbine will not change. Simultaneously, the turbulence intensity on beam 1 will increase due to the small-scale turbulence within the probe volume, and a detection signal will be visible on ΔTI_LOS. The influence of the wake can also be seen on the yaw misalignment estimation $\widehat{\mathit{\varphi }}$ which will deviate from its mean value in ambient flow. A reversed situation appears when a wake is affecting beam 2. A change in wind direction could coincide with a wake impingement on one of the measurement locations. In such a case, the algorithm cannot distinguish between the two. The current threshold values have been found manually by trying different thresholds and investigating the wake detection algorithm performance.

At the initialization the algorithm requires some wake-free observations to establish correct values of the running averages. The observations are used to calculate running averages of $\widehat{\mathit{\varphi }}$, ${\mathrm{TI}}_{{\mathrm{LOS}}_{\mathrm{2}}}$ and ${\mathrm{TI}}_{{\mathrm{LOS}}_{\mathrm{1}}}$. From our experience a few hours of wake-free data are sufficient. Note that the wind conditions during operation need to be similar to the conditions during initialization.

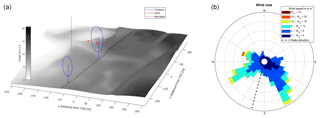
Figure 3 (a) Digital terrain model (DTM) of the Technical University of Denmark's (DTU) test site at Risø where the two turbines and the lidar are also shown. The black line indicates the wake direction of 195^∘. Zone 32 UTM coordinates centred at the Vestas V52 turbine were used. The DTM data were obtained from the Danish Map Supply (Agency for Data Supply and Efficiency, 2018). (b) Wind rose derived from sonic anemometer measurements on the meteorological mast during the experiment. The dashed black line indicates the direction of the Nordtank turbine.

3 Experimental setup

In this study, two field experiments executed at DTU's test site at the Risø Campus were analysed. The site consists of a row of turbines, of which two have been operative during the experiment: a Vestas V52 turbine with 850 kW rated power, a hub height of 44 m and a diameter of 50 m, and a smaller Nordtank turbine with 500 kW rated power, a hub height of 36 m and a diameter of 41 m. Further, data from a meteorological mast at a distance of 120 m = 2.3D_V from the Vestas V52 turbine, where D_V=52 m, have been used. The distance between the Vestas and the Nordtank turbine is 215 m (5.2D_N or 4.1D_V) at an angle of 195^∘ (clockwise from north), where D_N=41 m. A picture of the site can be found in Fig. 3.

The Vestas V52 turbine was equipped with a two-beam nacelle lidar by Windar Photonics during two distinct periods. Initially, one system was mounted between 5 December 2015 and 12 January 2016, and a second system was mounted between 29 March and 4 May 2016. The systems have identical properties. The opening angle between shaft axis and beam was 30^∘, and the focus distance was 37 m (implying that z_R=2.1 m). The objective of the experiment was to obtain yaw misalignment measurements from the lidars with special focus on the influence of the wake from the Nordtank turbine onto the Vestas V52. The data acquisition system of the turbine was logged turbine, mast and lidar data at a sampling rate of 35 Hz. For the analysis the data have been downsampled to 1 Hz.

The wind rose during the two experimental periods derived from a sonic anemometer mounted at the Vestas V52 hub height on the meteorological mast is shown in Fig. 3. The direction of wakes from Nordtank onto V52 is indicated as a dashed black line. Two dominant directions can be identified; the waked wind direction only represents a small share of the data.

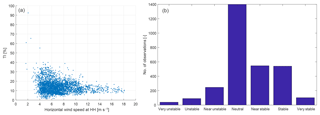
Figure 4 Hub height turbulence intensity versus wind speed (a) and count of the stability classes (b).

The turbulence intensity and a count of the stability classes that occurred during the experiment can be found in Fig. 4. The turbulence intensity has been determined by the hub-height sonic anemometer based on 10 min averages. The atmospheric stability has been calculated using the lowest sonic anemometer positioned at a height of 18 m based on 30 min averages. The calculation of the Obukhov length and the definition of the stability classes was taken from Peña et al. (2010). It can be seen that during the experiment the stability of the atmosphere was mainly neutral with a moderate number of stable and few unstable conditions.

4 Results

In this study, data are compared during normal power production of the turbines. To achieve this, lower thresholds on the minimum power production (i.e. > 0 kW), minimum rotor speed (i.e. > 16 rpm) and maximum pitch angle (i.e. < 23^∘) in each 10 min period were applied for the Vestas V52 turbine. Since the Nordtank turbine is stall regulated a lower threshold on minimum power production (i.e. > 0 kW) and minimum rotor speed (i.e. > 27 rpm) have been applied. The filtering removed 53.3 % of the data for both experiments. Additionally a filter was applied on the lidar data. Instances where the LOS speed could not be determined from the Doppler spectra have been summed within a 10 min period. If more than 10 % of the data (or 60 measurements) were missing, the 10 min period was rejected. Instances where four or more consecutive unavailable measurements occurred on any of the two beams were also discarded. Whether a measurement is available or not was decided internally by the lidar system and depended on carrier-to-noise ratio and the Doppler peak shape and area. This led to a discard of an additional 1.8 % of the data.

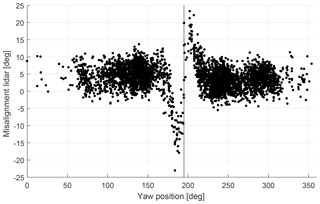
Figure 5 Lidar-estimated 10 min mean yaw misalignment $\widehat{\mathit{\varphi }}$ as function of turbine yaw position. The vertical black line indicates the position of the upstream Nordtank turbine. A clear influence of the wake on the misalignment estimates around the wake sector can be seen.

Next, the influence on yaw misalignment estimates of a wake emitted by the Nordtank turbine onto the Vestas V52 is investigated. The derived 10 min mean misalignment $\widehat{\mathit{\varphi }}$ as function of yaw angle of the turbine can be seen in Fig. 5.

The vertical black line indicates the position of the Nordtank turbine. It can be seen that outside the wake sector the misalignment ranges around a mean misalignment of 5^∘. Inside the wake sector large deviations from the mean misalignment can be observed. In situations where the right half of the rotor (at yaw position <195^∘) experiences a wake, LOS 2 will be affected by a reduced wind speed. Thus, a negative influence on the misalignment estimates by the lidar can be observed. Deviations of up to 30^∘ can be seen. Similar behaviour can be recognized when the wake affects the left part of the rotor (at yaw position >195^∘). Here, the deviation is smaller, but a clear influence is still visible.

An example of the two spectra are shown in Fig. 6. The red spectrum was measured in the free flow and shows a higher wind speed and a slender peak compared to the blue spectrum which is affected by a wake. The reduced wind speed and increased turbulence inside the wake leads to a lower LOS speed and a larger width of the Doppler spectrum compared to the red spectrum. Both spectra were gathered during the same 1 min interval. Thus, the same ambient turbulence conditions can be assumed for the two measurement locations.

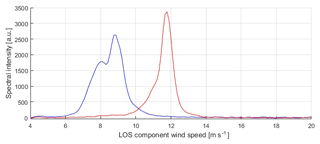
Figure 6 Example of two lidar Doppler spectra gathered during the same 1 min interval. The red spectrum is measured in the free flow, while the blue spectrum is affected by a wake. For the blue spectrum, the reduced wind speed and increased spectral width can clearly be seen. The spectra are averaged over 1 min.

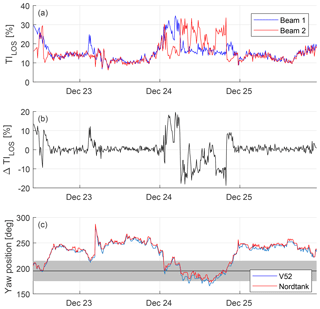
Figure 7 Example time series of TI_LOS (a), ΔTI_LOS (b) and the yaw positions of the two turbines (c). The black horizontal line and the grey shading in the bottom plot indicate the wake position (i.e. 195^∘) and a band of $\mathrm{195}{}^{\circ }\pm \mathrm{20}{}^{\circ }$, respectively.

A time series result of the detection parameters over 3 days can be found in Fig. 7. The top two panels show TI_LOS and ΔTI_LOS, while the bottom panel shows the yaw position of the two turbines. The horizontal black line and the grey shading indicate the wake sector. In general, it can be seen that if both turbines are positioned outside the wake sector, TI_LOS on both beams is approximately equal, i.e. ΔTI_LOS≈0. Thus, no significant difference of the turbulence levels within the lidar probe volumes is detected. As soon as both turbines yaw into a wake situation deviations of TI_LOS between beam 1 and beam 2 can be detected. For example, on 23 December the wind direction changes such that the Vestas V52 is in a half-wake situation, in which the left half of the rotor is affected based on their yaw positions. In this case a spike in TI${}_{{\mathrm{LOS}}_{\mathrm{1}}}$ can be identified. This corresponds to increased small-scale turbulence originating from the wake flow within the probe volume of beam 1 which is not present on beam 2. Hence, a positive increase in ΔTI_LOS can be observed. Similarly, the half-wake situations on the right half of the rotor on 24 December lead to higher TI${}_{{\mathrm{LOS}}_{\mathrm{2}}}$ than TI${}_{{\mathrm{LOS}}_{\mathrm{1}}}$.

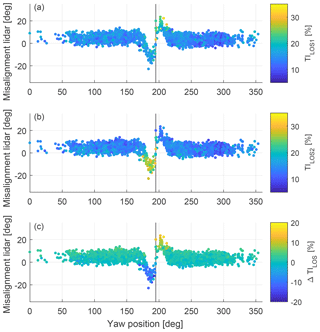
Figure 8 Lidar-estimated 10 min mean yaw misalignment $\widehat{\mathit{\varphi }}$ as function of turbine yaw position. (a) TI${}_{{\mathrm{LOS}}_{\mathrm{1}}}$, (b) TI${}_{{\mathrm{LOS}}_{\mathrm{1}}}$ and (c) ΔTI_LOS. The vertical black line indicates the position of the upstream Nordtank turbine (at 195^∘).

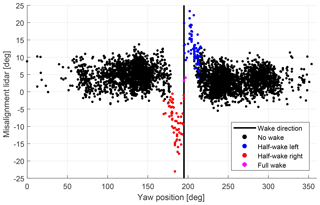
Figure 9 Lidar-estimated 10 min mean yaw misalignment $\widehat{\mathit{\varphi }}$ as function of turbine yaw position. The vertical black line indicates the position of the upstream Nordtank turbine. Detected waked situations are shown as coloured dots.

An overview of the measured TI_LOS and ΔTI_LOS against the yaw position of the Vestas V52 turbine can be seen in Fig. 8. Here, parallel observations to the previous figure can be made. If the turbine is yawing at angles corresponding to half-wake conditions on the right half of the rotor (i.e <195^∘), high values for TI${}_{{\mathrm{LOS}}_{\mathrm{2}}}$ and negative ΔTI_LOS can be observed. This case reverses for half-wake situations on the left half of the rotor where high TI${}_{{\mathrm{LOS}}_{\mathrm{1}}}$ and positive ΔTI_LOS can be noticed. For the full-wake case, increased TI_LOS on both beams appears and ΔTI_LOS shows values that are comparable to non-wake, ambient flow conditions. It can also be seen that for non-wake cases ΔTI_LOS is slightly positive. This is due to the mean misalignment which reduces the LOS speed on beam 1; see left illustration in Fig. 1. Thus, the ratio TI${}_{{\mathrm{LOS}}_{\mathrm{1}}}$ is slightly increased compared to TI${}_{{\mathrm{LOS}}_{\mathrm{2}}}$.

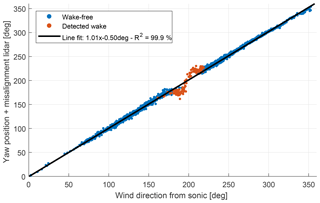
Figure 10 10 min mean wind direction correlation between the meteorological mast sonic anemometer and the wind direction estimate from the lidar, i.e. lidar misalignment + yaw position of the turbine. Outside the wake sector a high degree of similarity can be observed. The identified wake situations lead to a bias. The line fit is performed on wake-free data only.

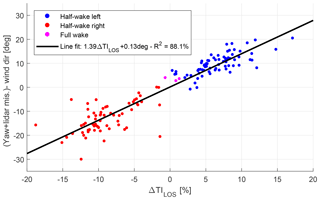
Figure 11 Difference between absolute wind direction estimated from the lidar (i.e. lidar misalignment + turbine yaw position) and sonic anemometer versus the detection parameter ΔTI_LOS. Only the observations in which a wake has been identified are shown. The line fit indicates that the data fit well to a linear regression model.

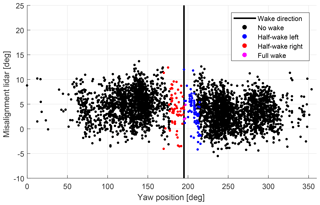
Figure 12 Lidar-estimated 10 min mean yaw misalignment $\widehat{\mathit{\varphi }}$ as function of turbine yaw position. The vertical black line indicates the position of the upstream Nordtank turbine. Detected wake situations have been corrected according to the relationship found in Fig. 10.

The next figure presents the results of the detection algorithm; see Fig. 9. Again, the misalignment derived from the lidar measurements is plotted against the yaw position of the Vestas turbine. Periods where a wake is detected in the inflow are shown as coloured dots and distinguished as left half-wakes (beam 1 is affected by a wake), right half-wakes (beam 2 is affected) and full wakes where both beams measure a wake influence. It can be seen that all detection results are clustered around the position of the upstream Nordtank turbine where a wake is expected. Also, all negative deviations from the mean misalignment are identified as right half-wakes and all positive deviations as left half-wakes. The recognized full wakes lie very close to the vertical black line and show no significant discrepancy from the mean misalignment. However, only three full-wake situations were identified. This can be explained by the different rotor sizes and the position of the focus points of the lidar, which are located towards the edges of the Vestas V52 rotor.

It can be observed that all detected wake situations are centred around the wake sector. This means that no free-flow conditions have been falsely detected as wake situations by the algorithm. In addition, all situations in which the lidar is affected by the wake have been detected correctly. Towards the edge of the wake sector possible false or missed detections could have occurred. However, this cannot be verified since no alternative method to measure the location of the wake was available during the experiment.

Next, the detected results will be analysed in detail and the misalignment will be corrected with the help of the undisturbed wind direction measurement from a sonic anemometer mounted on the close by meteorological mast at the hub height of the Vestas V52 turbine; see Fig. 3. First, the correlation between the wind direction estimation from the lidar and the measurement from the sonic will be compared. The absolute wind direction can be obtained by adding the lidar misalignment measurement to the yaw position of the turbine. Both the turbine and the sonic anemometer have been carefully aligned to north. The resulting correlation can be seen in Fig. 10.

It should be noted that outside the wake sector the two signals show a high degree of similarity. The fitted line, which has been fit using the wake-free observations only, shows a unity slope with a very small offset of 0.5^∘. The root mean squared error is 2.53^∘. However, the measurements which are affected by a wake show the characteristic deviations that could also be seen in Fig. 5. This suggests that the flow assumptions that are used to derive the lidar misalignment are valid if no wakes are impinging the field of view, but a correction is necessary for wake situations. If the correlation, which is observed for non-wake observations, also holds for wake cases, the difference between the wind direction from sonic anemometer and lidar can only originate from the influence of the wake.

Thus, we suggest the use of the wind direction measurements from the sonic anemometer to obtain an empirical relationship between the detection parameter ΔTI_LOS and the bias in the wind direction measurements from the lidar and the sonic anemometer. This relationship is shown in Fig. 11. It can be observed that detected half-wake situations on the right side of the rotor show persistent negative ΔTI_LOS and vice versa. The identified full wakes both have a wind direction error and ΔTI_LOS close to zero.

A linear line has been fitted to the data, which shows that the data follow approximately a linear relationship. The derived equation is as follows: 1.39ΔTI_LOS+0.13^∘. This equation can now be used to correct the misalignment measurements by the lidar that are affected by a wake. Wake-free observations remain unchanged. The result of the correction can be seen in Fig. 12, and by comparing this figure with Fig. 9 the performance of the correction method can be evaluated. After the correction it is seen that the misalignment estimates, which are affected by wakes and previously showed large deviations from the mean misalignment, are now within the range of the wake-free observations. It was possible to adjust both the positive and negative spikes stemming from half-wakes on the left and right side of the rotor. The full-wake situations are only affected slightly because their difference in TI_LOS is small. The root mean squared error (RMSE) of the difference between the wind direction estimate from the sonic anemometer and the lidar (compare Fig. 10) is 4.47^∘ for the wake-free data and 7.68^∘ for the wake-affected data. After the correction has been applied to the identified wake situations, the RMSE of the wake-affected data has dropped to 4.22^∘, which is similar to the RMSE of the wake-free data.

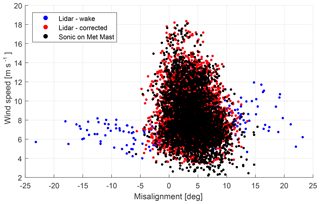
Figure 13 Comparison between the 10 min mean yaw misalignment estimated from the lidar and the sonic on the meteorological mast (Met Mast). The observations affected by wakes are shown in blue and the corrected measurements in red.

Finally, an overview of the misalignment measurement is compared to the misalignment measured by the sonic anemometer at the meteorological mast. The misalignment versus wind speed is shown in Fig. 13. It can be seen that both the lidar and sonic measurements follow a similar trend. At low wind speeds the misalignment is centred around 5^∘, and as the wind speed increases the misalignment reduces. The influence of wakes on the lidar measurements has been identified and corrected as previously described. Slightly lower wind speed measurements from the sonic anemometer can be observed, which are caused by the wake of the Vestas V52 turbine on the meteorological mast (at yaw angles of 289^∘).

5 Conclusions

In this study we investigate how nacelle-mounted cw lidar systems can be used to estimate wind turbine misalignment even in inflow with a wake. Lidars offer the possibility of remotely sensing the inflow of turbines and avoid the flow disturbance caused by the blades and the nacelle which are usually encountered by nacelle wind vanes or sonic anemometers. Correct alignment of turbines is important because power production losses can be mitigated.

Nevertheless, due to the limitation of measuring only the LOS component of the approaching wind, a lidar system needs to measure at several positions in front of the wind turbine and assumptions about the flow field need to be made to derive quantities of interest. A common assumption is that of horizontal homogeneity of the inflow which states that at positions of the same height the wind vector is equal. This assumption is usually satisfied if the terrain is flat and homogeneous and if appropriate averages over time, commonly 1 to 10 min averages, are taken. It can, however, be violated if a wake from a neighbouring turbine is impinging the inflow, and the reduced wind speed inside a wake leads to a bias on the horizontal wind speed and wind direction.

Here, this influence is evaluated experimentally from two measurement campaigns, where a two-beam cw nacelle lidar was mounted on a Vestas V52 turbine which is exposed to a wake from a slightly smaller neighbouring turbine. It was shown that within the wake sector the influence of wakes induces biases on the misalignment measurement as large as 30^∘ from the mean misalignment outside the wake sector. Half-wake situations on the right side of the rotor lead to negative deviations, while half-wakes on the left side result in positive bias. This implies that if lidars were to be used for turbine yaw alignment, the observations that are affected by wake interaction must be identified and corrected.

The wake detection algorithm presented here is based on the spectral-broadening effect of the lidar Doppler spectrum because of small-scale turbulence within the probe volume. Since lidar systems perform measurements over a rather large measurement volume, high-frequency turbulent fluctuations are attenuated and are not visible in the LOS speed signal but lead to a widening of the Doppler spectrum. The small-scale turbulence generated inside wake flows will lead to more broadening than in the ambient flow. Thus, by comparing the spectral width of the Doppler spectrum at different focus locations, wakes that affect the field of view of one or both beams can be detected. The detection parameter used in this study is the LOS-equivalent turbulence intensity TI${}_{\text{LOS}}=\frac{{\mathit{\sigma }}_{\mathrm{LOS}}}{v_{\mathrm{LOS}}}$.

The performance of the algorithm is presented in Fig. 9 and shows that all lidar observations that measure the wind direction wrongly can be identified. Only very few full-wake situations were observed due to the size difference of the turbines. To correct the wind direction measurements affected by wakes an empirical relationship between lidar turbulence measurements and the deviation of the lidar wind direction from the true direction measured by a sonic on a nearby mast was established. It was shown that the absolute wind direction measurements from both sensors have a high degree of correlation for non-wake cases. A linear relationship between the difference in TI_LOS between the two beams and the difference in wind direction between the lidar and the sonic was found. Applying this relationship to the measurements affected by wakes yielded a correction of the large misalignment deviations experienced during half-wake situations.

Thus, we have shown how the detrimental effect of wake on nacelle lidar measurements can be mitigated. However, for the correction it was necessary to utilize the undisturbed wind direction measurements from a mast-mounted sonic anemometer. The turbines that have been used in this experiment are smaller than current utility-scale turbines. Hence, it was possible to use short lidar focus distances which result in a narrow probe volume, and the spectral widening is due to turbulence of a very small length scale. In this experiment average spectra of 1 min were sufficient to detect the wake-induced turbulence. If the lidar is installed on larger turbines, where larger focus distances are required, the probe volume will increase, and shorter averaging times might be necessary to only detect turbulence generated within the wake. Shorter averaging times lead to increased signal noise and can have an effect on the estimation of the Doppler spectrum variance.

The ambient turbulence intensity during the experiment was moderate, while the stability of the atmosphere was mainly neutral. Thus, the increased turbulence within the wake flows could be distinguished from ambient flow. On a site with higher ambient turbulence conditions, this distinction could be more difficult. One approach would be to decrease the averaging time of the lidar Doppler spectrum, which would only allow small-scale fluctuations to contribute to the width of the Doppler spectrum. These small-scale fluctuations occur mainly in wake flows, while the ambient turbulence generated by the terrain or obstacles are of larger scale.

The proposed correction method relies on the availability of a reference instrument, which is not always present. The linear relationship between error in wind direction and ΔTI_LOS is supported by experimental data for the test site considered here. So far no experience has been gathered on how this relationship changes when the lidar is used at a different site. More experimental data are need to build an understanding of how site-specific parameters, like turbine spacing, rotor diameter or ambient turbulence levels, influence the relationship. Ideally, a universal relationship that is valid for different turbines and sites could avoid the usage of a reference instrument.