Reducing cost uncertainty in the drivetrain design decision with a focus on the operational phase

In order to identify holistically better drivetrain concepts for onshore wind turbine application, their operational behavior needs to be considered in an early design phase. In this paper, a validated approach for estimating drivetrain-concept-specific unplanned operational effort and risk based on open-access data is presented. Uncertain influencing factors are described with distribution functions. This way, the poor data availability in the early design phase can be used to give an indication of the concept's choice influence on the unplanned operational wind turbine behavior. In order to obtain representative comparisons, a Monte Carlo method is applied. Technical availability and drivetrain-influenced unplanned operational effort are defined as evaluation criteria. The latter is constituted by labor, material and equipment expenses. By calculating the range of fluctuation in the evaluation criteria mean values, this approach offers an indication of the inherent risk in the operational phase induced by the drivetrain concept choice.

This approach demonstrates that open-access data or expert estimations are sufficient for comparing different drivetrain concepts over the operational phase in an early design stage when using the right methodology. The approach is applied on the five most common state-of-the-art drivetrain concepts. The comparison shows that among those concepts the drivetrain concept without a gearbox and with a permanent magnet synchronous generator performs the best in terms of absolute drivetrain-influenced unplanned operational effort over the drivetrain's lifetime as well as in terms of the inherent risk for the assumptions made. It furthermore makes it possible to give insights into how the different drivetrain concepts might perform in future applications in terms of unplanned operational effort. Exemplarily the impacts of higher torque density in gearboxes, a change to moment bearings and adjusted coil design in electrically excited generators have been analyzed. This analysis shows that the superiority of synchronous-generator concepts manifested in historic data is not entirely certain in future applications. Concluding, this approach will help to identify holistically better wind turbine drivetrain concepts by being able to estimate the inherent risks and effort in the operational phase.

1 Introduction

Decreasing subsidies, fierce competition with fossil power stations and photovoltaics puts the wind industry under high development and cost pressure. The wind turbine drivetrain as the sum of the energy-converting components between hub and transformer has a significant influence on the wind turbine's properties and behavior. Up to 50 % of the wind turbine's investment cost can be accounted for by the nacelle and its components (Mone et al., 2015). More importantly over 80 % of the unplanned failures of a wind turbine can be traced back to nacelle components (Reder et al., 2016). It is estimated that cost arising during the operational phase can add up to the initial investment cost (Luers et al., 2015).

Today's market presents a variety of drivetrain concepts. However, no statement about the best concept is yet possible. Especially the concept's performance in the operational phase is hard to estimate upfront. Its components are designed for a 20-year lifetime with not fully known load cases, maintenance and mounting accuracy. These are especially not known during the conceptualization phase. However, the greatest influence on the product's, in this case the drivetrain's, success can be exerted in the early phases of product development as its cornerstones are set here (Ehrlenspiel et al., 2014). Furthermore, effort for design modification rises exponentially with the product's maturity level (Ehrlenspiel et al., 2014). To identify superior products in an early phase of the product development, this paper argues that a concept-specific estimate of the unplanned maintenance effort and inherent risks is required. This can be made in a two-step approach. First of all, the drivetrain concept characteristics which have an influence on the operational phase of an onshore wind turbine have to be identified. This includes the description of their influence. Subsequently a method for modeling this behavior in an early design stage needs to be identified and implemented. This paper aims at providing information about the expected drivetrain component and concept operational behavior as well as a statement about the certainty of this behavior. The outcomes of this paper provide a wind turbine designer with a tool to identify holistically better drivetrain concepts for onshore application in an early design stage and furthermore to evaluate possible places for improvement and the concept's influence on the operational phase.

In the following, an approach for estimating drivetrain-concept-specific inherent risk of unplanned maintenance effort and technical availability is developed and presented. In Sect. 2, a short literature review is given. Section 3 presents the paper's object of reflection. Section 4 introduces the general model approach. In Sect. 5, the developed model and its underlying assumptions are introduced. The required validation is stated in Sect. 6, and in Sect. 7, a concept comparison is conducted. Finally, Sect. 8 gives a conclusion and an outlook.

2 Literature review

The evaluation of the unplanned operational behavior of wind turbine drivetrains in an early design phase is rare. Nevertheless, some drivetrain concept comparisons focusing on the operational phase are available in the literature. Most of them derive statements based on the evaluation of empirical databases, which are unfortunately not open access (Carroll et al., 2014b). Thereof, failure mode and effects analysis and derivates (Cevasco et al., 2018; Ozturk et al., 2018) as well as Monte Carlo simulations (McMillan and Ault, 2010; Dalgic et al., 2015) are the most commonly used methods. They highly rely on empirical databases which are not available in the early phase of product development. Alternatively, other authors use fixed average failure rates from one source to model the components operational behavior (Carroll et al., 2014a, 2017). The representativeness of analysis based on fixed average failure rates from one source is questionable (as shown by Carroll et al., 2015b). In addition, available concept comparisons mostly lack an indication of the certainty of their results. In an uncertain situation it helps to at least have an indication of the level of uncertainty and its source(s). Furthermore, the above-presented approaches are not suitable for a technology comparison if aiming for identifying room for improvement from a technological perspective. Statements about the lifetime behavior as well as about scalability are mostly not in the scope of the available literature. Hence this publication presents an approach for deriving scalable and more representative estimations about drivetrain-concept-specific operational behavior based on publicly available data.

3 Object of reflection

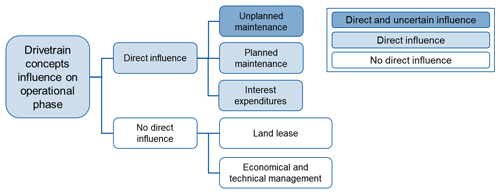
This paper aims to quantify the influence of the drivetrain concept choice on the operational expenditures over the wind turbine's lifetime as well as on the turbine's technical availability. The focus lies on the consideration and quantification of uncertain aspects of unplanned operational effort. In this approach, the drivetrain is seen as the sum of the energy-converting components between the wind turbine's hub and transformer. This means the operational behavior of the chosen suspension system, gearbox, generator and converter design is considered. Figure 1 gives an overview of aspects generally influencing the operational expenditures of a wind turbine. They are divided into aspects that are directly influenced by the drivetrain concept choice and aspects that are uncertain.

Figure 1 Factors influencing the operational phase of a wind turbine.

The focus of this investigation lies on drivetrain-influenced uncertain aspects. Unplanned maintenance is the most prominent factor which is uncertain and directly influenced by the concept choice. Therefore, it is solely considered in this approach. Unplanned maintenance is defined as an unpredictable component breakdown which urgently needs unscheduled activities. Unpredictable component breakdown makes this aspect a highly uncertain and risk-inherent situation. It can have a multitude of influencing factors like the component design, unknown loading conditions, system interaction, manufacturing and mounting accuracy. When trying to find help in the literature, data are often anonymized, and therefore samples cannot be characterized in a sufficient way (Cevasco et al., 2018). More importantly different studies come to contradictory statements about the components' failure behavior (Ozturk et al., 2018; Carroll et al., 2017). Unplanned maintenance includes unscheduled activities that need to take place in the case of a component breakdown. The actions needed and the related effort are mostly uncertain and again are influenced by a multitude of factors. Failure type, accessibility, weather, spare parts, technicians and equipment availability can influence the unscheduled activities. Once more, literature studies seldom provide information about durations (downtime, repair times) and reasons for the extent of the activities. Samples are defined in an unsatisfactory way. These complex and uncertain features make it impossible to precisely calculate the unplanned maintenance effort and availability of a drivetrain concept in an early design phase with reasonable effort. Still, this is a major characteristic of a drivetrain concept which has to be considered in the concept decision.

In this paper the early design phase is defined as the phase in the product development process where design decisions for the concept are made (cf. step three of VDI 2221; VDI, 1993). This phase is characterized by a high degree of complexity, uncertainty and information deficits. In the status quo, this highly important decision is mainly based on experience of the deciding engineers. This can be especially critical when evaluating completely new ideas differing to the former product generation. Known in this decision are the rated power of the wind turbine, its rotor diameter, the wind class it is developed for and the possible drivetrain concepts.

4 Model approach

This section presents the approach used for estimating drivetrain-concept-specific unplanned maintenance effort and technical availability in an early design stage. The approach needs to fulfill the following requirements:

• deal with the poor availability of concept-specific information in the literature and early design stage

• allow estimates of the technologically inherent impact the drivetrain concept choice has on the operational phase

• consider and evaluate the most relevant influencing factors in the operational phase

• be applicable to state-of-the-art drivetrain concepts

• be scalable in terms of rated power and rotor diameter

• be applicable to incremental inventions and new concept ideas.

This approach is based on publicly available studies about the drivetrains' operational phase. As mentioned in Sect. 3, these studies sometimes come to contradictory statements and are not always transparent about the cause of failure or downtime. Therefore, the model is based on several assumptions. The first assumption is that not all influencing factors leading to a failure can be modeled individually. Therefore, failure detectability, weather or site-specific impacts as well as the maintenance strategy itself are not considered directly. Furthermore, it is assumed that all available study results from the literature represent realistic component behavior, as it is mostly not known what conditions the underlying wind turbines experienced or which specific failure mechanism occurred. The next assumption is that this behavior is mainly influenced by technological choice. It is assumed that these influencing factors are randomly distributed. Failure rate, downtime, failure severity, and duration of repair and replacement are modeled as uncertain factors. In order to include all available information, continuous distributions are chosen to fit the observed data for depicting the uncertain factors if possible. Parameters for fitting the distributions are estimated based on a maximum likelihood method. It is assumed that the entire drivetrain consists of repairable assemblies, which means each assembly can sustain more than one failure and is “as good as new” after repair or replacement. In reality, repair never reaches the reliability of a new component. Still, this assumption makes it possible to model the life of a fictional wind turbine based on the derived distributions.

A statistical approach, the Monte Carlo method, is utilized for deriving representative results as it makes it possible to calculate a multitude of fictional wind turbine lives. It has the ability to conduct a high number of random experiments based on uncertain influencing variables. The basis for this method is the law of large numbers. It says that, by performing a large number of experiments, the mean of the results will come close to the expected value. This approach is suitable for the present problem as it is constituted by different uncertain factors that can be described by continuous distribution functions. Furthermore, this method offers the possibility of obtaining insights into not just the expected value but also the result's occurrence probability. The inverse-transform sampling method is used for generating random numbers with a defined distribution. This way, a sufficient number of fictional wind turbine operational lifetimes are simulated for every component based on the distributions derived from literature data. This is done for all relevant drivetrain components.

In this approach, technical availability AV [%] is influenced by uncertain factors including mean time to failure and duration of repair, replacement or downtime; see Eq. (1):

$$\begin{array}{}\text{(1)}& \mathrm{AV}\left(i\right)={\displaystyle \frac{{\sum }_{s=\mathrm{1}}^{\mathrm{3}}{\sum }_{j=\mathrm{1}}^{\mathrm{4}}{\sum }_{d=\mathrm{1}}^{\mathrm{4}}{\mathrm{do}}_{j,d,s}\cdot f_{j,d,s}\left(i\right)}{h}}.\end{array}$$

In this equation, j indicates the component (main bearing, gearbox, generator, converter), d the specific design (e.g., for the permanent magnet synchronous generator) of the component and s the failure severity (minor repair, major repair or major replacement). The number of failures in the specific year i is represented by $f[\mathrm{failure}/\mathrm{a}]$. The downtime each failure leads to is represented by $\mathrm{do}[h/\mathrm{failure}]$ in year i. The variable h is used to show the number of hours a calendar year has [$\mathrm{8760}\mathrm{h}/\mathrm{a}$]. Technical availability is therefore calculated as the percentage of the year's time where the drivetrain could technically provide electricity if wind conditions are met.

Estimating the drivetrain-influenced unplanned operational effort (DUOE) [EUR] is a bit more complex; see Eq. (2):

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathrm{DUOE}\left(i\right)& =\sum _{s=\mathrm{1}}^{\mathrm{3}}\sum _{j=\mathrm{1}}^{\mathrm{4}}\sum _{d=\mathrm{1}}^{\mathrm{4}}{f}_{j,d,s}\left(i\right)\cdot (\mathrm{LE}\left({\mathrm{dr}}_{j,d,s},{\mathrm{nt}}_s,w\right)\\ & +\mathrm{ME}\left(m_{j,d,s}\right)+\mathrm{EE}\left(c\right({\mathrm{we}}_{j,d,s},{\mathrm{dr}}_{j,d,s}\left)\right)).\end{array}\end{array}$$

It is constituted by labor, material and equipment expenses. Labor expenses LE [EUR] are influenced by the uncertain factor duration of repair or replacement dr [h], which is component, design and failure severity dependent. LE is furthermore influenced by the number of technicians needed nt [–], which is failure severity dependent. Finally, the wage of a technician w [EUR/h] impacts the labor expenses. Material expenses ME [EUR] are determined taking the severity of the failure and component-design-specific investment cost m [EUR] into account. Equipment expenses EE [EUR] consider expenses for a crane to enable component exchange. The crane needed and its associated expenses c [EUR] are dependent on the component-design-specific weights we [kg] and the duration of repair or replacement dr [h].

Both component-design-specific weight and component-design-specific investment cost scale with rated power and rotor diameter and therefore with the field of application. They are calculated based on the NREL Wind Turbine Design Cost and Scaling Model (Fingersh et al., 2006), which is a cost and mass regression model based on industry data. As visible in Eq. (2) these two variables have an impact on the material expenses as well as on the equipment expenses leading to a high impact on DUOE. Therefore, the use of these inputs makes this approach scalable in terms of rated power and rotor diameter.

Table 1 Failure severity distinction based on Carroll et al. (2014b) and model implementation.

5 Model implementation

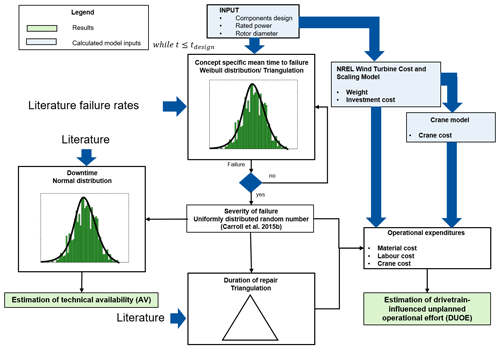
The following section gives insights into how the model idea is implemented. Some general assumptions are presented at the beginning before the model procedure is introduced. Failure rate, downtime, failure severity, duration of repair and replacement are modeled as uncertain factors. Collected data about these factors are allocated to the different drivetrain components and their design. Design-unspecific information is allocated to the components in general. This unspecific information is later considered for all component designs. This allows the most to be made out of the available data while not favoring one design or distorting the result. Figure 2 shows an overview of the model's structure and the underlying assumptions. Model input is constituted by the component design, rated power and rotor diameter. One model iteration represents the operational behavior of a drivetrain from installation until the end of its design lifetime.

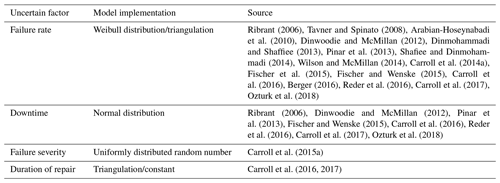
For every operational year component failure occurrence and failure time are calculated. It is assumed that the components' failure behavior follows a Weibull distribution. This is a common assumption for technical systems. Weibull distribution makes it possible to reveal the main nature of the failure being premature, random or due to wear-out. Weibull parameters for the failure behavior of the different components are determined based on the mean time to failure. The mean time to failure as the reciprocal of failure rates is derived from available failure rates from the literature (for sources see Table 2). Unfortunately, the sample cannot be characterized completely. The sample is mainly constituted by data recorded between 1990–2014 for a rated power of up to 4 MW. A maximum likelihood method is applied for deriving the Weibull parameters for the mean time to failure. It is assumed that failure rates for the different component designs already contain subsequent faults due to the chosen system. Therefore, components can be modeled independently from each other.

Figure 2 Overview of model structure.

Table 2 Literature sources used for model parameterization.

In the case of a failure, its severity needs to be determined. Referring to Carroll et al. (2014b) failure severity categorizes failures due to their impact on material cost. It distinguishes between minor repair, major repair and major replacement. The first row in Table 1 gives the definition of the failure severity types used. Failure severity is considered with a uniformly distributed random number and a percentual distribution determined from Carroll et al. (2015b). Unfortunately, this distribution is deduced from an offshore database.

Failure severity affects the downtime of a wind turbine. For every failure severity category downtime is modeled in a distinctive way. Downtime due to minor repair is modeled with a constant value from the literature (Carroll et al., 2017). For major repair and replacement, downtime is assumed to follow a normal distribution. Distribution parameters are derived from the literature (please see Table 2). The accumulated downtime over the drivetrain's design lifetime now allows for an estimate of the effect of the unplanned drivetrain failures on AV.

According to Eq. (2) the estimation of DUOE is constituted by material, labor and equipment expenses (please see Table 1). Material expense estimation is described in the following. Minor repair is repair which leads to material cost of up to EUR 1000. In this model material expenses are therefore neglected. Major repair is implemented as a random number between EUR 1000–10 000. According to Carroll et al. (2014b) major replacement is a replacement which leads to material cost exceeding EUR 10 000. In the model it is assumed that the entire component needs to be exchanged if this failure type occurs. Material expenses are therefore modeled as the investment cost of the failed component. Component- and design-specific component investment cost is calculated based on rated power and rotor diameter using the NREL Wind Turbine Design Cost and Scaling Model (Fingersh et al., 2006).

Labor expenses, another part of DUOE, are mainly influenced by the duration of the action. Failure severity and component-specific action duration for major repair and replacement is modeled with the help of triangulation. Here the modus is assumed to equal the mean. For minor repair a fixed action duration per component is taken into account based on Carroll et al. (2017). Repair is carried out by two technicians. Replacement measures require three technicians due to safety reasons. A constant hourly wage is assumed.

Finally, equipment expenses need to be estimated. It is assumed that no additional crane is needed for minor and major repair as the onboard equipment can be used. An additional crane is used to enable the component exchange for major replacements. For crane cost estimation, a parameterized model is developed which chooses the crane needed based on component weight and the hub height the component needs to be lifted to. Crane data are based on Liebherr cranes (Liebherr, 2019). Component weight is estimated based on the NREL Wind Turbine Design Cost and Scaling Model (Fingersh et al., 2006). For some components an exchange is only possible if further components are dismounted; this fact is considered in the crane decision. The crane is leased for the time the replacement takes.

By adding up the three expenses a concept-specific estimate of DUOE is possible.

6 Model validation

Verification and validation are performed by comparing modeled values with published data combined with a general reasonability check. At the beginning, the failure behavior is in focus. Components in the following designs are in the scope: moment, trunnion, three-point and four-point suspension system, two- and three-stage gearbox, permanent magnet synchronous generator (PMSG), electrically excited synchronous generator (EESG), and doubly fed induction generator (DFIG) as well as partially and fully rated converter. The initial null hypothesis is that all component failure behavior can be described by a Weibull distribution. Due to the small sample size, an Anderson–Darling goodness-of-fit test is conducted. This test is applicable to samples with a minimum size of four. The null hypothesis for a Weibull distribution is not rejected for the two-stage gearbox and three-stage gearbox with a three-point suspension system, all generator types, and partially rated converters with a 5 % significance level. Hence, they are modeled by a Weibull distribution. The three-stage gearbox with a four-point suspension system follows a log-normal distribution again confirmed by an Anderson–Darling goodness-of-fit test. For all main-bearing arrangement designs as well as fully rated converters, either this test is not applicable or the null hypothesis is rejected. Therefore, triangulation is applied. An Anderson–Darling goodness-of-fit test supports the assumption that component downtime can be described by a normal distribution. Unfortunately, no design-specific modeling for downtime is possible due to a lack of data.

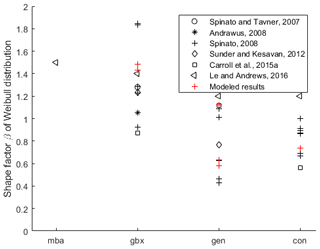
Figure 3 Components' failure behavior from the literature and model results described by the Weibull shape factor (Spinato and Tavner, 2007; Andrawus, 2008; Spinato, 2008; Sunder and Kesavan, 2012; Carroll et al., 2015b; Le and Andrews, 2016).

There are a few publications available in the literature where the failure behavior of different wind turbine drivetrain sub-assemblies has been empirically evaluated and described by a Weibull distribution. Figure 3 shows the shape factor of the Weibull distribution for different component failure behavior from the literature and the modeled results. A first look reveals a wide spread in the shape factor in the literature indicating ambiguous failure behavior. It needs to be considered that the Weibull shape factors are not distinguished in the component design. Model results are component design specific and show different behavior for the different designs which is in line with literature values. This way the chosen distributions and distribution parameters are confirmed.

Not only the failure behavior but also the general model results should be validated, meaning the modeled mean DUOE and AV. The mean values are calculated based on results of 1 000 000 iterations. According to the law of large numbers, the average results converge to the expected value, the more iteration results are taken into account. Therefore, the calculated mean values can be seen as approximations of the expected value of DUOE and AV on a lifetime basis. The expected value is the value which is the arithmetic mean and therefore the most probable outcome.

Figure 4 Scaled meta-study about yearly mean DUOE and model results (Nitsch et al., 2010; Mone et al., 2013; Chaviaropoulos et al., 2014; McKenna et al., 2014; IRENA, 2018; Reichenberg et al., 2018; ISE Fraunhofer, 2018).

The literature does not directly provide these numbers needed for the comparison; therefore, they are approximated in the following. Yearly operational cost can vary between 2 %–4.2 % of the initial investment cost of the wind turbine (Nitsch et al., 2010; ISE Fraunhofer, 2010, 2012, 2013; Hobohm et al., 2013). Two further created meta-studies indicate that operational expenditures over the year vary from 30 to 52 EUR/kWa or 0.5–2.68 cents/kWh (Nitsch et al., 2010; Mone et al., 2013; Chaviaropoulos and Natarajan, 2014; McKenna et al., 2014; IRENA – International Renewable Energy Agency, 2018; Reichenberg et al., 2018; Fraunhofer ISE, 2018). These meta-studies give the impression that operational expenditures vary substantially. Unfortunately, the sources do not indicate their samples in a sufficient way. Therefore, only a scale comparison can be conducted for validation. Of yearly operational expenditure, 44 %–55 % is associated with maintenance and repair (Luers et al., 2015). For the comparison, planned maintenance effort and unplanned effort for other wind turbine components need to be excluded. This leads to the assumption that a quarter of the maintenance and repair expenses are caused by DUOE.

Table 3 Considered drivetrain concept characteristics and their market share (Hernandez et al., 2017).

A corrected meta-study is shown in Fig. 4. In addition to the literature values, this figure also depicts the calculated values for currently available drivetrain concepts (A–E). The concept characteristics including their market share are presented in Table 3. All drivetrain concepts are designed for a rated power of 3 MW and a rotor diameter of 120 m, representing the currently installed onshore fleet in Germany. This application will be used in all coming analysis in this paper if not stated differently. With an average yearly mean DUOE value of 4.59 EUR/kWa the modeled results are in between the meta-study results varying between 3.3 EUR/kWa and 5.808 EUR/kWa. Furthermore, the industry standard of technical availability above 97 % is achieved for all analyzed concepts. So, the general model results are reasonable.

7 Concept comparison

The validation section showed that there are significant differences in mean DUOE for different drivetrain concepts. This section allows the better understanding of underlying reasons for these differences. In a second step, the developed framework is used to address possible future developments and their impact on mean the DUOE of different drivetrain concepts.

Table 4 Modeled Weibull parameter for failure behavior of different drivetrain components in different designs.

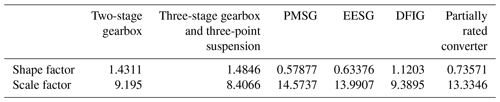
First of all, the component-design-specific failure behavior is evaluated. Table 4 presents the Weibull parameters derived from available historical literature sources (see Table 2) for the different components in their different designs. It is visible that the PMSG, EESG and partially rated converter mainly followed early failure behavior in the past. They have a shape factor below 1. Statistically, one failure will occur during their lifetime as indicated by their scale factor, whereas the two-stage gearbox, three-stage gearbox with a three-point suspension system and DFIG have mainly been attributed to wear-out behavior. For these component designs statistically two failures will occur over their lifetime, indicated by their scale factor below 10. In this approach no specific failure mechanisms are discerned; they are aggregated into three failure types (premature, random or wear-out). For future research the derivation of failure-mechanism-specific Weibull distributions could be a highly interesting topic. This way specific improvements in specific component designs could be directly taken into account.

Figure 5 gives an overview of the calculated mean DUOE over the entire drivetrain's lifetime split into material, labor and equipment expenses share. All concepts and components have in common that the material expenses have the highest influence on mean DUOE followed by labor expenses. Equipment expenses, if modeled in the way presented, are less influential. Under the chosen assumptions direct-drive concepts (B and C) lead to the lowest mean lifetime DUOE. To explain this, a deeper look into different components in different designs is needed. Going from the bottom to the top of Fig. 5, it starts at the component main-bearing arrangement (mba). No direct influence of the main-bearing arrangement on the unplanned operational expenses is calculated. This can be explained by the mean time to failure used for the triangulation which is on the scale of 10⁶ years. Looking at the gearbox it is apparent that it is the component that is responsible for most of the unplanned operational expenditure of a drivetrain. This can be traced back to its failure behavior which indicates statistically two failures occurring during its lifetime and 24 % of these failures leading to major replacement (Carroll et al., 2015a). Due to fewer high rotating components, the two-stage gearbox is more reliable than both three-stage versions. Furthermore, the exchange of a two-stage gearbox is less expensive as the gearbox is lighter and has lower investment cost. A distinction between three-stage gearboxes with a three-point and a four-point suspension is discernible. Due to the non-torque loads entering the gearbox with a three-point suspension system, it is less reliable and leads to higher unplanned operational effort. Going further to the component generator it is visible that the EESG leads to the highest mean lifetime DUOE. Reliability-wise the PMSG and EESG seem to be on the same level. This is derived from the same labor expense level and Weibull parameters. Still, material expenses are higher for the EESG as its investment cost and therefore material expenses are higher. It is, furthermore, heavier than the direct-drive PMSG resulting in higher equipment expenses. Despite its higher failure rates, the DFIG results in lower mean DUOE than the direct-drive synchronous generators. As the DFIG combined with a three-stage gearbox operates in higher rotational input speed ranges and lower rated input torque ranges, it needs fewer pole pairs. This leads to a comparatively less complex, lighter and less expensive generator for the considered rated power and rotor diameter. The same argumentation is valid when comparing the results for the geared and direct-drive PMSG (A vs. B). Due to the higher rotational input speed and lower input torque, the generator needs fewer pole pairs and a less stiff structure. Looking into the behavior of the component converter it is visible that the converter has a minor influence on the overall expenses. The reason is the low number of needed replacements which usually lead to high expenses. This is in line with the literature which says that converter failures can often be solved remotely or with low effort.

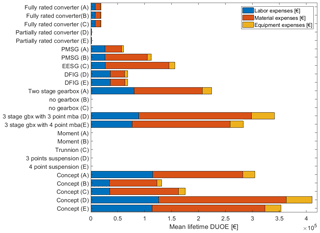
Figure 5 Drivetrain concept comparison based on 1 000 000 iterations for a 3 MW and 120 m rotor diameter design.

Table 5 shows the concept-specific DUOEs' lifetime impact on the total drivetrain lifetime effort. In this approach the total drivetrain lifetime effort consists of the mean lifetime DUOE and the calculated drivetrain-specific investment cost. The latter is based on calculations from NREL's Wind Turbine Cost and Scaling Model (Fingersh et al., 2006). Logistics and installation effort are not included as they cannot directly be assigned to the drivetrain. In the literature they are usually assigned to the entire wind turbine. Based on the underlying assumptions concept B seems to be the dominant concept in terms of total drivetrain lifetime effort for the considered application. Finally, the concept-specific mean lifetime DUOE share on the total drivetrain lifetime effort is presented. Based on the model results it is discernible that for geared drivetrains (concept A, D and E) the specific DUOE can account for up to a third of the total drivetrain lifetime effort. For direct versions (concept B and C), it is around 13 %.

Table 5 Concept-specific DUOEs' lifetime impact on the total drivetrain lifetime effort for the 3 MW 120 m rotor application.

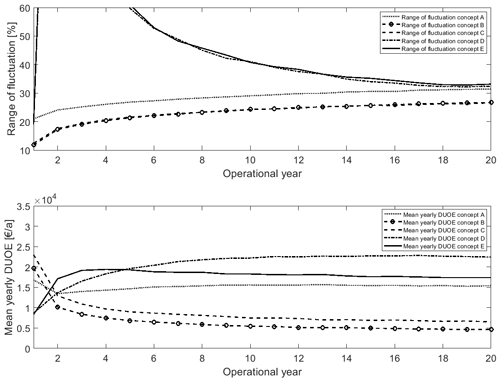
Figure 6 Mean unplanned yearly DUOE and yearly range of fluctuation in DUOE for different drivetrain concepts based on 1 000 000 iterations for a 3 MW, 120 m rotor diameter application.

The bottom plot of Fig. 6 gives an overview of the mean DUOE of the drivetrain concepts and their development over the lifetime. In order to explain the course of the graph in Fig. 6 the combination of the failure behavior of each component in the concept-specific design should be kept in mind as it has a high influence on DUOE. Please recall that Table 4 gives an overview of the modeled Weibull parameters for failure behavior of different drivetrain components. Concepts A, D and E all show a dominant wear-out behavior (high level of DUOE at the end of the lifetime) which can be traced back to the three-stage gearbox used. Furthermore, concepts D and E both have a DFIG, which additionally leads to the shown wear-out behavior. Interestingly random-failure behavior is visible for these three concepts, as the DUOE stays at a constant level after its infancy. Concepts A, B and C all use synchronous generators which all follow mainly an early failure behavior. This is visible in the course of the graph in Fig. 6, as it starts at a high level and decreases within the first years of operation. As visible in Fig. 5 the chosen converter concept has a minor impact onto the mean modeled lifetime DUOE. Accordingly, the impact on the course of Fig. 6 is negligible.

Still, mean values do not allow for a statement about the results certainty. In order to allow a statement about the certainty of this behavior, the range of fluctuation is calculated for a worst-case scenario. The range of fluctuation is defined as the concept's individual yearly standard deviation of DUOE divided by the mean concept's DUOE; see Eq. (3):

$$\begin{array}{}\text{(3)}& \mathrm{range}\mathrm{of}\mathrm{fluctuation}\left(i\right)=\sum _{j=\mathrm{1}}^{\mathrm{4}}{\displaystyle \frac{{\mathit{\sigma }}_{j,d}\left(i\right)}{{\mathit{\mu }}_{j,d}\left(i\right)}}.\end{array}$$

In Eq. (3) μ_j, d(i) depicts the mean DUOE of component j with design d in respective year i, whereas σ_j, d(i) depicts the standard deviation of DUOE for the component j in design d under investigation in respective year i. The worst case is defined as the sum of fluctuation in the individual components in the design under investigation, which however will unlikely come into effect. The range of fluctuation is an indicator of inherent risk as it gives an indication of the possible maximum deviation from the mean. For better vividness, the plot is cut at a range of fluctuation of 60. From an inherent-risk point of view, the direct-drive concepts perform best; please see the top plot of Fig. 6. Still, the worst case can be a maximum deviation of 10–30 times from the yearly mean DUOE. Risk of deviation rises until the end of the drivetrain's lifetime. The two three-stage gearbox concepts perform worse from a risk-inherent perspective. Especially concept D can have 560 times the mean yearly DUOE in a worst-case scenario in the early lifetime. Concept E can result in expenses of over 300 times the mean yearly value. It needs to be kept in mind that the failure behavior for gearboxes is derived from a lot more data points than the behavior of the other components. This can lead to a higher deviation as more possible applications are covered. A solely technical cause is questionable.

In order to bring the above-presented results into perspective, the historical input data are questioned. Experts have been consulted in order to evaluate if the data used still present today's technology behavior. It turns out that the wind turbine original equipment manufacturer (OEM) calculates with one gearbox exchange over the turbine's lifetime on average. The historical data sample used indicates less reliable behavior. One development which is not reflected in the data is the improved planned maintenance of gearboxes which has advanced today's gearboxes' reliability. This has been mentioned as a lesson learned from previous experience. Furthermore, gearbox OEMs more and more design gearboxes which can be repaired up the tower. This development makes it possible to reduce the number of major gearbox replacements and have major repair instead. This effect has not been captured in the historical data yet.

Besides evaluating today's technology, it is even more interesting to have a look at possible future developments. Though the authors are not able to anticipate future development with certainty, they can utilize the presented method to give indications of possible trends. Figure 7 presents results about future development based on assumptions whose grounding is experience and developments already visible today. The application for future wind turbines is characterized by a rated power of 5 MW and a rotor diameter of 150 m, being the average wind OEMs announced in 2020 for onshore application (Bundesverband Wind Energie, 2020).

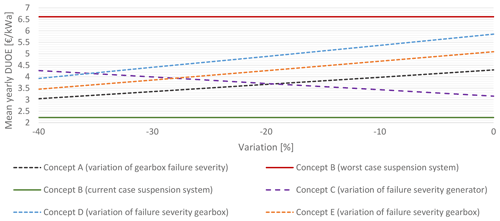
Figure 7 Impact of future development on the yearly mean DUOE for a 5 MW 150 m rotor diameter onshore application.

A current trend in gearbox development is an increased torque density especially for higher-rated power applications. Higher power density allows the use of smaller gears which lead to smaller and lighter gearboxes. More compact gears are less exposed to material imperfections, and therefore a smaller probability of fatigue failures exists. It is assumed that exact calculation methods for the strength against the predominant failure modes of the given gear sets are available as downsizing leads to a reduction in the remaining safety reserves, and this effect could also lead to reduced reliability. In order to enable higher torque densities, plain bearings are seen as an enabler for more compact gearbox design. Introducing this new bearing design might decrease reliability. Combining all mentioned factors, it is assumed that future gearbox reliability behavior stays constant but corrected in terms of the above-mentioned reduced number of major gearbox replacements due to the age of the input data. A sensitivity study varying the number of major replacements and having major repair instead for concepts A, D and E is shown in Fig. 7.

For concept C a reliability deterioration for the generator is expected. The turbine OEM currently using this concept introduced a technology shift in the coil material and manufacturing in order to decrease the investment cost. The wires are welded together, and aluminum is used instead of copper (Enercon GmbH, 2017.). First of all, experience needs to be gained with this new technology in combination with meeting increased loading requirements (higher input torques). Therefore, failure severity might increase for the generator of concept C in Fig. 7.

For the concepts with a moment bearing a reduced reliability is possible for the future. Unlike the other bearing concepts this suspension concept is comprised in one point of support, which leads to a disproportionate increase in dimensions if input loads rise. This makes it likely to be switched to plain bearings. Moreover, this concept needs high manufacturing and mounting accuracy, which is more difficult to meet if dimensions increase. Both aspects make it likely to have reduced reliability. As the main-bearing arrangement failure occurrence was negligible in the former analysis, a best and a worst case are plotted in Fig. 7. The best case is defined as a suspension system reliability similar to that historically reported. The worst case is defined by triangulation with a mean time to failure of 10 years (min to max is 0–20 a). Furthermore, all reported failures are interpreted as major replacement. This assumption is based on expert interviews.

Figure 7 depicts possible future technological developments and their impact on the mean yearly DUOE of different drivetrain concepts. A variation of 0 % depicts the mean yearly DUOE based on the same assumptions as the results for the previously presented 3 MW application. It is visible that the order of advantageousness is not changed due to the change in the application requirements. However it is furthermore visible that, at certain combinations of developments, the order of advantageousness of the concepts is changed. It is up to the reader to assess how realistic these developments are. Concluding from Fig. 7, the superiority of synchronous-generator concepts manifested in historic data is not entirely certain in future application. It mostly depends on a myriad of developments in the different technologies.

Another approach to derive future drivetrains' reliability behavior introduced by Moghadam et al. (2020) identifies positive aspects of geared drivetrain concepts which might be dominant in certain applications (Moghadam and Nejad, 2020). They conduct a reliability comparison for future drivetrain concepts for a 10 MW offshore floating application. By simulating rotor torque and generator electromagnetic torque oscillation for different drivetrain concepts and argumentatively analyzing the influence on the drivetrains' failure modes, they identify several effects of a middle- or high-speed concept using a gearbox which probably reduce the coincidence of frequencies and vibration. This way they argue geared concepts might lead to higher reliability in that application if new failure modes due to the presence of a gearbox do not mitigate them. They furthermore take the entire life cycle into consideration and see further advantages (weight, investment cost and efficiency) of using a geared concept.

8 Conclusion and outlook

In order to identify holistically better drivetrain concepts for onshore wind application, their operational behavior needs to be taken into account in an early design phase. In this paper, a validated approach for estimating drivetrain-concept-specific risk of unplanned maintenance effort and technical availability based on open-access data is presented. By describing uncertain influencing factors with distributions, the poor data availability in the literature and in the early design phase can be used to obtain an indication of the concepts choice influence on the unplanned operational wind turbine behavior. This approach furthermore allows the inclusion of information about the concept's behavior from different applications and sources. By using triangulation, incremental innovation and completely new concept ideas can be evaluated as well. In order to obtain representative comparisons a Monte Carlo method is applied. This way a multitude of drivetrain lifetimes can be modeled following the distributions behavior. The most relevant influencing factors are considered by modeling failure rate, downtime, failure severity, and duration of repair and replacement as uncertain factors. Technical availability and drivetrain-influenced unplanned maintenance effort are defined as evaluation criteria. By calculating the range of fluctuation in the results, this approach offers an indication of the inherent risk in the drivetrain-influenced unplanned maintenance effort which is a central criterion. Scalability is given, as material and equipment expenses are scaled with wind turbine rotor diameter and rated power. This approach shows that openly accessible data or expert estimations are sufficient for comparing different drivetrain concepts over the operational phase in an early design stage.

The application of this approach on five state-of-the-art drivetrain concepts for a 3 MW, 120 m rotor diameter wind turbine demonstrates that for all concepts and components the material expenses have the highest influence on mean DUOE followed by labor expenses. Equipment expenses, if modeled in the way presented, are less influential. Overall direct-drive concepts lead to the lowest mean DUOE over the drivetrain's lifetime. This indication is confirmed when looking at the inherent risk of deviations from these estimated mean values. A gaze into the future showed that the superiority of synchronous-generator concepts manifested in historic data will not be entirely certain in future application. Exemplarily the impacts of higher torque density in gearboxes, a change to moment bearings and adjusted coil design in electrically excited generators have been considered.

Still, it has to be considered that this analysis is based on sometimes very old and maybe outdated data especially when describing the failure behavior. Furthermore, the extent of the databases for different component design deviates a lot which might bias the result. Unfortunately, a component-design-specific distinction of the failure severity has not been possible based on open-access data up to now. For adapting this method to new concepts, a physically based approach could be developed which would make it possible to estimate probability distributions for the uncertain factors. In the presented approach no specific failure mechanisms are discerned; they are aggregated into three types. For future research it could be a highly interesting topic to derive failure-mechanism-specific Weibull distributions. Moreover, dependency between failures of different components is only indirectly taken into account; this could be addressed additionally. Another possible direction for research is to include the influence of the maintenance strategy as well as site or park specific impacts in the evaluation. Moreover, this approach only takes the operational phase into account. For identifying holistically superior drivetrain concepts, the entire drivetrain life cycle needs to be considered. The authors intend to develop approaches for estimating the concepts' behavior in all life cycle phases of the drivetrain which can deal with the poor data availability in the early development phase. This way they will be able to evaluate different trade-offs within the drivetrain design. Nevertheless, this approach can already assist in drivetrain concept decision-making by being able to quantify the inherent technological risks in the operational phase.