Measurement of the turning behaviour of tethered membrane wings using automated flight manoeuvres

Flexible membrane wings for kite sports, paragliding and airborne wind energy are highly manoeuvrable aerodynamic devices. The manoeuvrability can be quantified by the achievable turning rate of the wing and the dead time between the steering input and the actual flight dynamic response. In this paper, we present an onboard sensor system for measuring the position and orientation of a tethered membrane wing and complement this with an attached low-cost multi-hole probe for measuring the relative flow velocity vector at the wing. To ensure well-defined flow conditions and high quality of the measurement data, the wings selected for testing were towed by a vehicle with a constant speed along a straight track during periods of low ambient wind speeds. A flight control algorithm was adapted from the literature to execute automated, repeatable figure-eight flight manoeuvres and measure the steering gain and the dead time as functions of the steering input. The experimental study confirms the turning behaviour known from kite sports and airborne wind energy applications and provides reproducible quantitative data to develop and validate simulation models for flexible, tethered membrane wings.

1 Introduction

Flexible membrane wings are commonly used for applications where mobility, low weight, low cost and fast deployment are essential. Prominent examples are kiteboarding, snowkiting, paragliding and airborne wind energy (AWE). The latter is an emerging renewable energy technology that is considered complementary to conventional wind energy because it can access wind at higher altitudes (Bechtle et al., 2019; Kleidon, 2021) while using only a fraction of the material resources required for conventional wind turbines (IRENA, 2021). AWE systems based on flexible membrane wings are currently being developed by the companies SkySails, Kitenergy and Kitepower, all using pumping cycle operation to harvest wind energy (Nelson, 2019). The development of this specific wing type is still a largely iterative empirical process based on the experience of kite designers and subjective prototype tests.

Unlike a fixed wing, a flexible membrane wing does not have sufficient bending stiffness in span- and chordwise directions and must be supported by a bridle line system. Instead of using individually actuated aerodynamic control surfaces, the entire wing functions as a morphing control surface, actuated by the tethers or the bridle line system. Asymmetric actuation is generally used for steering, while some designs also allow for symmetric actuation of the rear bridle lines for powering and depowering (Oehler and Schmehl, 2019). A notable exception is the ram-air wings of SkySails, which, until recently, were steered by roll control and not by wing morphing (Paulig et al., 2013). Because of the general C shape of a bridled membrane wing, any changes to the geometry of the bridle line system also entail a deformation of the tensile membrane structure. In addition to this actuation-induced morphing, a membrane wing is also subject to aeroelastic deformations.

The spanwise twisting of leading edge inflatable (LEI) kites during sharp turning manoeuvres is illustrated in Fig. 1.

Figure 1 Time-lapse composite photo of a 6 m² power kite for sport applications performing a sharp turn to the left and subsequent loop manoeuvre, taken from the towing vehicle, from Lange (2018) (left panel). Photo of a 25 m² power kite for airborne wind energy applications performing a turn to the right during a mast-based launch manoeuvre, reported by Oehler and Schmehl (2019) (right panel). Both photos illustrate the spanwise twist deformation exhibited by LEI kites. The extreme deformation in the right photo does not occur in regular flight operations but resulted from mast-based launch attempts, shown here only to visualize the wing twist mechanism.

The characteristic deformation is caused by pulling one steering line and releasing the other, with the two lines being attached to the trailing edges of opposing wing tips. Breukels (2011) used an aero-structural model to simulate the deformation of an LEI kite during a turning manoeuvre. Breukels (2011) concluded that this particular wing morphing is key to high manoeuvrability, proposing the following mechanism. Pulling on a wing tip while releasing the other locally increases the angle of attack of the pulled tip while decreasing the angle of the other tip. Also, pulling increases the effective vertical area of the respective wing half, while releasing decreases this area for the other half. Because of the twisting of the wing, the aerodynamic centres of the tip regions are shifted relative to each other. The combination of these effects leads to a resulting aerodynamic side force and a yawing moment. The side force and the yawing moment are both important for initiating the turning manoeuvres. The described mechanism was confirmed by Bosch et al. (2014) using a fluid–structure interaction model of an LEI kite.

The effect of a steering input on the turn rate of a flexible membrane kite can be described by simple mechanistic models without considering a twist deformation or roll of the wing. A first “turn rate law” was formulated and experimentally validated for roll-controlled ram-air kites by Erhard and Strauch (2012, 2013b). Applying a simplified equilibrium of aerodynamic side force and centrifugal force during a turning manoeuvre, they found that the turn rate is linearly proportional to the product of steering line actuation and apparent wind speed at the kite. An extended formulation included an additional term accounting for the effect of gravity. Jehle (2012) and Jehle and Schmehl (2014) showed that this correlation approach also applies to LEI kites. Ruppert (2012) used a moment equilibrium at the wing tips to express the proportionality factor in terms of geometric and aerodynamic coefficients of the kite. Fagiano et al. (2013c, 2014) used a similar mechanistic model to identify another version of the turn rate law describing the rate of change in the velocity angle of the kite as a function of the steering input. Nowadays, the turn rate law underlies many control algorithms for automated flight operation of flexible membrane wings (Vermillion et al., 2021; Fagiano et al., 2022). Flight tests have revealed that the dynamic response of the wing to a steering input can be significantly delayed, and some of the algorithms (Baayen, 2012; Rontsis et al., 2015; Costello et al., 2015, 2018; Wood et al., 2015) account for this delay with an additional term.

To experimentally determine the proportionality factor in the turn rate law, two approaches have been pursued: tow tests and flight tests using a fixed ground station with a winch. Wind tunnel measurements are not feasible because the dynamic flight state during a turning manoeuvre cannot be recreated in a static set-up, such as that used in de Wachter (2008) and Rementeria Zalduegui (2019) for measuring the aerodynamic performance of kites, and because a test section can spatially not accommodate a kite flying a turning manoeuvre. However, for outdoor measurements, the varying wind environment presents a challenge to the reproducibility of the measurement data. This is particularly important when the data are intended for parameter identification in simulation models (de Groot et al., 2011). The pioneering work of Erhard and Strauch (2012, 2013a) for SkySails was based on operational data from large ram-air kites of up to 320 m² wing surface area that were used to pull ships. The data included the steering input and the apparent wind speed at the kite, measured with an anemometer in the suspended kite control unit, as well as the turn rate of the wing. Jehle (2012) and Jehle and Schmehl (2014) used data sets from LEI kites with 14 and 25 m² wing surface area that were operated automatically in pumping cycles to generate electricity. A suspended kite control unit was used to steer the kite (see Fig. 1) and, in contrast to the concept of SkySails, also to power and depower the kite by changing the wing's angle of attack. Next to the wing's steering input and turn rate, the apparent wind speed was measured with a Prandtl tube suspended in the bridle line system of the kite (van der Vlugt et al., 2013). Oehler et al. (2018) used similar kites but also measured the angles of the apparent wind velocity vector, using two orthogonal flow vanes, next to the previously mentioned properties and the position and orientation of the kite over time. They performed two different types of tests: fully automatic pumping cycle operation and flight manoeuvres at lower altitudes manually controlled from the ground. Borobia et al. (2018) performed flight tests with a 13 m² LEI kite that was manually controlled via four lines by a pilot on the ground, listing recorded time histories of steering input and rotation of the wing in space. Borobia-Moreno et al. (2021) substituted the simple Prandtl tube used in the earlier tests with a five-hole probe to also measure the inflow angles. Turning behaviour was not measured. Rushdi et al. (2020a, b) used a 6 m² LEI kite in a tow test set-up to harvest data for machine learning. The kite was controlled by a suspended control unit that was attached to the towing vehicle via a short tether segment. Castelino et al. (2022) used a 12 m² LEI kite that was steered manually with a control bar from a fixed ground point, estimating the tether force using deep neural network models. Schelbergen and Schmehl (2024) investigated the swinging motion of a kite with a suspended control unit, as illustrated in Fig. 1 (right), while flying turning manoeuvres. The swinging motion in terms of pitch and roll was modelled and compared to flight test data. The turning performance was not assessed in this work.

Hummel (2017) and Hummel et al. (2019) systematically investigated and quantified the effect of symmetric actuation for powering and depowering flexible membrane kites. The research was part of the TETA (Test and Evaluation of Tethered Airfoils) project, in which a tow test set-up for reproducible flight experiments with flexible membrane wings was developed (Duotone Kiteboarding, 2019; Kite Magazin, 2019; The Kiteboarder, 2019). To generate a constant and uniform flow field, the tests were conducted on days with very low ambient wind speeds. The towing vehicle and the trailer were equipped with several sensors and actuators to generate control inputs, fly reproducible manoeuvres and measure various parameters.

The objective of the present study is to expand on this work by measuring the turning behaviour of kites using automatic and reproducible flight manoeuvres under controlled environmental conditions. The presented material is based on the PhD research of the first author (Elfert, 2021). The paper is organized as follows. In Sect. 2, the measurement concept is presented. In Sect. 3, the test set-up is detailed, and in Sect. 4, the data acquisition is described. This is followed by a presentation and discussion of the experimental results in Sect. 5 and an elaboration of conclusions in Sect. 6.

2 Measurement concept

To simulate a constant and uniform wind environment, the tests were executed on days with very low ambient wind, towing the trailer-mounted test bench with constant speed along a straight track. The set-up is illustrated schematically in Fig. 2, showing the different subsystems, components and information flows.

Figure 2 Towing test schematic, adapted from Hummel et al. (2019).

The test bench is mounted on a trailer and pulled by a vehicle. The kite is controlled by a pilot from within the vehicle, using a conventional control bar and visual feedback from a video camera. The manual steering input is converted into digital signals transmitted to the test bench, which then actuates a second control bar from a pivot head. Sensors on the kite and part of the actuation mechanisms are fed back to the control cabinet. Servomotors provide force feedback to the pilot. This specific decoupling of the pilot's control input in the towing vehicle from the actuation of the control bar on the test bench was chosen to allow for three different control modes: “fully manual”, “semi-manual” and “fully automated”. Because of the digitization of the pilot's steering inputs, mixing them with outputs from the control algorithms is possible.

2.1 Measured properties

The analysis of the turning behaviour is based on the recorded time histories of the steering input δ, the apparent wind speed v_a and the resulting turn rate $\dot{\mathit{\psi }}$ of the wing. The power setting u_p is considered an additional parameter in the analysis. Figure 3 details the definition of the power setting for symmetric actuation (left) and steering input for asymmetric actuation (right).

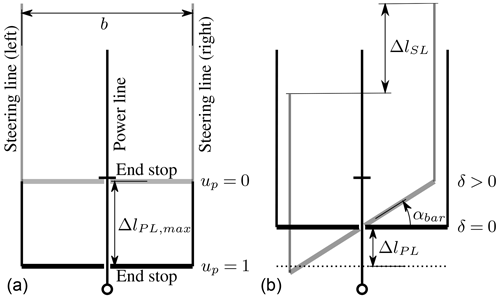
Figure 3 Definition of the power setting u_p showing symmetric actuation in fully powered and depowered states (a) and steering input δ with associated asymmetric actuation at a halfway-depowered kite (b).

The fully powered state is defined by u_p=0, while the fully depowered state is defined by u_p=1. When fully depowered, the length difference Δl_PL between power and steering lines is at the maximum value Δl_PL,max. At any relative power setting $\mathrm{0}\le u_{\mathrm{p}}\le \mathrm{1}$, the relative steering input is defined as

$$\begin{array}{}\text{(1)}& \mathit{\delta }=\sin {\mathit{\alpha }}_{\mathrm{bar}},\end{array}$$

causing a length difference Δl_SL of the two steering lines. Accordingly, δ can vary between −1 and 1.

Figure 4 illustrates the kinematic properties of a kite K performing crosswind flight manoeuvres while being towed by a test bench B along a straight track.

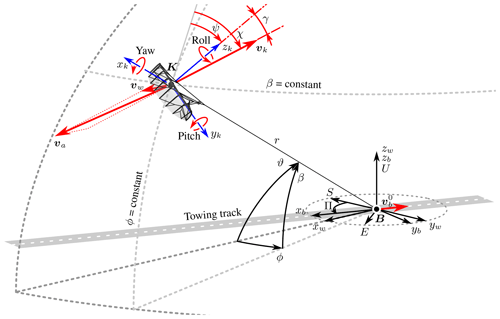
Figure 4 Kinematic properties of the kite K and the towing test bench B for a vanishing ambient wind speed $v_{\mathrm{w}}^{\mathrm{0}}$.

The kite and the test bench velocities relative to a fixed point on the ground are denoted as ${\mathit{v}}_{\mathrm{k}}^{\mathrm{0}}$ and ${\mathit{v}}_{\mathrm{b}}^{\mathrm{0}}$, respectively. The flight velocity of the kite relative to the moving test bench is thus given by

$$\begin{array}{}\text{(2)}& {\mathit{v}}_{\mathrm{k}}={\mathit{v}}_{\mathrm{k}}^{\mathrm{0}}-{\mathit{v}}_{\mathrm{b}}^{\mathrm{0}}.\end{array}$$

The wind velocity relative to the moving test bench is given by

$$\begin{array}{}\text{(3)}& {\mathit{v}}_{\mathrm{w}}={\mathit{v}}_{\mathrm{w}}^{\mathrm{0}}-{\mathit{v}}_{\mathrm{b}}^{\mathrm{0}},\end{array}$$

where ${\mathit{v}}_{\mathrm{w}}^{\mathrm{0}}$ is the ambient wind velocity. Because the tow tests aim to simulate specific ambient wind conditions, the relative wind velocity v_w is also denoted as simulated wind velocity. The corresponding relative wind reference frame ($x_{\mathrm{w}},y_{\mathrm{w}},z_{\mathrm{w}}$) moves with the test bench and has its z_w axis pointing vertically upwards and its x_w axis pointing in the direction of the wind velocity relative to the moving test bench. Also included in Fig. 4 is the south-east-up (SEU) Earth-fixed reference frame, and the body-fixed reference frame of the test bench is shown as ($x_{\mathrm{b}},y_{\mathrm{b}},z_{\mathrm{b}}$), with its x_b axis aligned with the towing velocity ${\mathit{v}}_{\mathrm{b}}^{\mathrm{0}}$. The rotation of the x_b axis from the south direction is described by the angle Π. Equation (3) indicates that at low ambient wind velocity ${\mathit{v}}_{\mathrm{w}}^{\mathrm{0}}$, the simulated wind velocity v_w can be controlled well by the towing velocity ${\mathit{v}}_{\mathrm{b}}^{\mathrm{0}}$.

The apparent wind velocity v_a experienced by the kite, also denoted as inflow velocity, can be defined either in the moving or in the Earth-fixed reference frame as

$$\begin{array}{}\text{(4)}& {\mathit{v}}_{\mathrm{a}}={\mathit{v}}_{\mathrm{w}}-{\mathit{v}}_{\mathrm{k}}={\mathit{v}}_{\mathrm{w}}^{\mathrm{0}}-{\mathit{v}}_{\mathrm{k}}^{\mathrm{0}}.\end{array}$$

The practical challenge in measuring v_a is not only the attachment of the flow sensor to the deforming kite system while maintaining a well-defined orientation but also the placement of the sensor in such a way that the flow is not disturbed by the presence of the kite or the sensor itself (Oehler and Schmehl, 2019). The position of the kite in the wind reference frame is defined in terms of spherical coordinates (r, ϕ, β), where r is the radial distance, ϕ is the azimuth angle and β is the elevation angle.

Figure 4 also includes the body-fixed reference frame ($x_{\mathrm{k}},y_{\mathrm{k}},z_{\mathrm{k}}$) of the kite and the associated rotations, denoted as yaw, pitch and roll. With this particular choice of x_k, y_k and z_k axes, the reference frame coincides with the body-fixed reference frame of the test bench ($x_{\mathrm{b}},y_{\mathrm{b}},z_{\mathrm{b}}$) when the kite is in its launch position at ϕ=0 and ϑ=0, sitting on its trailing edge, with the longitudinal axis of the kite pointing upwards. This enables an easy check-up of the calculated orientation angles before starting a measurement. Assuming a fully tensioned tether and a flight motion of the kite on the spherical surface with radius r, the orientation of the kite in a local tangential plane can be described by the heading angle ψ, while the orientation of the kite velocity can be described by the course angle χ, which is coupled to the time derivatives of the azimuth and elevation angle by a kinematic relation:

$$\begin{array}{}\text{(5)}& \mathit{\chi }=\arctan \left({\displaystyle \frac{\cos \mathit{\beta }\dot{\mathit{\varphi }}}{\dot{\mathit{\beta }}}}\right).\end{array}$$

This concept of describing the orientation of the kite and its velocity on a spherical surface originates from the field of navigation and has been applied in prior work on flight control (Jehle and Schmehl, 2014; Fagiano et al., 2014; Fechner and Schmehl, 2018). Both angles are measured clockwise from the upward (zenith) direction, ranging from −180 to +180°. Within this framework, the yaw rate of the kite is identical to the rate of change $\dot{\mathit{\psi }}$ of the heading angle, which is also denoted as the turn rate. The yaw angle and the velocity angle only differ if the kite is not aligned with the direction of flight. The drift angle γ describes the difference between the velocity and orientation of the kite:

$$\begin{array}{}\text{(6)}& \mathit{\chi }=\mathit{\psi }+\mathit{\gamma }.\end{array}$$

The direction of the apparent wind velocity in the body-fixed reference frame of the kite is described by the angle of attack α and the sideslip angle β_s. The angle of attack of the wing is measured in the x_kz_k plane of the kite, while the sideslip angle is measured in the y_kz_k plane.

2.2 Turn rate law

The basic structure of the turn rate law can be derived from a simple mechanistic model of the kite performing a turn. This scenario is illustrated in Fig. 5 for a kite tethered to a fixed point on the ground.

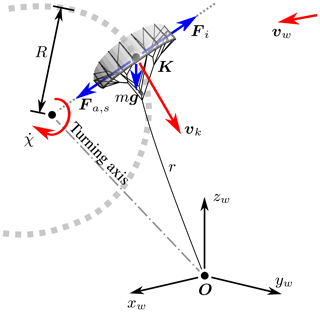
Figure 5 Kite performing a left turn with a turning radius R tethered to a fixed point O on the ground.

The model can be used equally for the towing test but using the relative kinematics introduced in Sect. 2.1. For moderate steering actuation, it can be assumed that the angle of attack of the wing tip is linearly dependent on the steering input δ. As a consequence, also the aerodynamic side force depends linearly on the steering input, which can be expressed as

$$\begin{array}{}\text{(7)}& F_{\mathrm{a},\mathrm{s}}=C{v}_{\mathrm{a}}^{\mathrm{2}}\mathit{\delta },\end{array}$$

where all constant problem parameters are combined into a single constant C. How exactly the side force F_a,s is generated, whether by roll or by asymmetric deformation of the wing, is not important for this analysis. Next, we can conclude from Fig. 5 that the rate of change $\dot{\mathit{\chi }}$ of the course angle and the kite velocity v_k are coupled by a kinematic relation:

$$\begin{array}{}\text{(8)}& v_{\mathrm{k}}=\dot{\mathit{\chi }}R,\end{array}$$

here R denotes the turning radius. For a steady flight on a trajectory with a constant curvature, the force equilibrium in the y_k direction of the body-fixed reference frame of the kite can be formulated as

$$\begin{array}{}\text{(9)}& F_{\mathrm{a},\mathrm{s}}+m\mathit{g}\cdot {\mathit{e}}_{y,k}=mR{\dot{\mathit{\chi }}}^{\mathrm{2}},\end{array}$$

where m represents the mass of the kite, g the gravitational acceleration, e_y,k the unit vector in the y_k direction and the term on the right-hand side the centrifugal force F_i. Inserting Eqs. (7) and (8) into Eq. (9) leads to the course rate law:

$$\begin{array}{}\text{(10)}& \dot{\mathit{\chi }}=g_{\mathrm{k}}{\displaystyle \frac{v_{\mathrm{a}}^{\mathrm{2}}}{v_{\mathrm{k}}}}\mathit{\delta }+{\displaystyle \frac{\mathit{g}\cdot {\mathit{e}}_{y,\mathrm{k}}}{v_{\mathrm{k}}}},\end{array}$$

where $g_{\mathrm{k}}=C/m$ is a non-dimensional constant denoted as steering gain, depending on the geometry of the kite but also on various variable influencing parameters such as the line length, the position of the kite in the wind window, the inflow velocity, and the power setting or the force in the steering lines. Oehler et al. (2018) showed on the basis of experimental data that the drift angle γ is generally constant except for short periods at the start and end of a turning manoeuvre. From Eq. (5), it can thus be concluded that the time derivatives of the course and heading angles are largely identical. This leads to the following formulation of the turn rate law:

$$\begin{array}{}\text{(11)}& \dot{\mathit{\psi }}=g_{\mathrm{k}}{\displaystyle \frac{v_{\mathrm{a}}^{\mathrm{2}}}{v_{\mathrm{k}}}}\mathit{\delta }+{\displaystyle \frac{\mathit{g}\cdot {\mathit{e}}_{y,\mathrm{k}}}{v_{\mathrm{k}}}}.\end{array}$$

Assuming a fast-flying kite with v_k≫v_w, the apparent wind speed can be approximated well by the flight speed of the kite, which leads to the basic, most frequently used formulation of the turn rate law:

$$\begin{array}{}\text{(12)}& \dot{\mathit{\psi }}=g_{\mathrm{k}}{v}_{\mathrm{a}}\mathit{\delta }+{\displaystyle \frac{\mathit{g}\cdot {\mathit{e}}_{y,\mathrm{k}}}{v_{\mathrm{a}}}}.\end{array}$$

Experimental studies have shown that the flight dynamic response of the kite is delayed from the steering input, which is a dynamic effect that is not covered by the steady-state derivation above. The dead time is also not constant but depends on various influencing parameters. For this reason, we use the following expanded formulation of the turn rate law in the present study:

$$\begin{array}{}\text{(13)}& \dot{\mathit{\psi }}\left(t\right)=g_{\mathrm{k}}\left(t\right)v_{\mathrm{a}}\left(t\right)\mathit{\delta }(t-d(t\left)\right),\end{array}$$

where d is the additional dead time. In this formulation, the influence of the gravitational force on the rotation rate is neglected, as proposed by Erhard and Strauch (2013b) for kites in crosswind flights where the gravitational forces are of minor importance compared to the dominant aerodynamic forces.

The steering gain g_k and dead time d represent the a priori unknown kite-specific parameters that depend on the current flight state of the kite described by the line length, the position in the wind window, the inflow velocity, and the power setting or the force in the steering lines.

2.3 Measurement procedure

The tow tests were conducted on the asphalted shoulders of a straight, 1.5 km long runway section. The kite is positioned behind the test bench with taut lines for launching, sitting on its trailing edge. Once the test rig accelerates, the kite lifts off and is manually steered towards the zenith. The desired simulated wind velocity is set via the cruise control of the towing vehicle and controlled using data from a weather station mounted on the vehicle roof and the test bench's global navigation satellite system (GNSS) sensor. When reaching the target speed, the pilot uses a foot switch to activate the flight controller to perform reproducible flight manoeuvres. The activated controller allows a fully automatic or semi-automatic flight depending on the specific settings. Once the end of the runway is reached, the flight manoeuvres are stopped, and the vehicle performs a U-turn while the kite is controlled manually. The same procedure is then repeated in the reverse tow direction and so forth, so measurement runs of any length can be conducted.

To accurately determine the steering gain and dead time, sufficient statistical averaging data must be collected for the entire range of wind power densities. This can be achieved by performing repeated figure-eight manoeuvres. Starting with u_p=0.4, the power setting increases in discrete steps until reaching u_p=1. For each step, a sufficient number of manoeuvres have to be executed. The shape of the figure-eight trajectories is adjusted so that the manoeuvres do not extend too far towards the lateral edge of the wind window. This region denotes the region of the spherical surface on which the kite can perform quasi-steady flight manoeuvres (Schmehl et al., 2013). Because the reaction to steering inputs at low power settings may not be sufficient to counteract the gravitational force, it can happen that the kite can no longer be flown back into the wind window and drifts to the ground at the edge of the wind window. For high power settings, the kite can accelerate to high speeds and overpower the edge of the wind window, leading to a stall and a subsequent crash of the kite. Both anomalies are prevented by using the robust flight control system presented in Sect. 4.1 for automated flight manoeuvres.

3 Test set-up

This section further details the test set-up, expanding on the work of Hummel (2017) and Hummel et al. (2019), adding an onboard sensor system to the kite. The purpose of this sensor is to acquire data about the flight state of the kite, including the position, velocity, orientation and apparent wind velocity at the kite, the latter of which is a key parameter affecting the aerodynamic forces.

Figure 6 Test bench and its main components (Elfert, 2021).

Figure 7 Details on the passive pivot unit connecting to the power line via a universal joint (Elfert, 2021).

3.1 Test bench

Figure 6 shows a rendering of the test bench that is assembled on a single-axle car trailer.

Two winches powered by servomotors are positioned in the centre of a frame made of aluminium profiles. Each motor is managed by a servo controller translating the commands received from the software via CAN and returning various status parameters of the motors. This also includes the rotational positions of the winches used to determine the length difference Δl_SL of the two steering lines. Each line is wound onto its winch and, from there, guided to the attachment points on the kite via two pulleys that are part of the pivot unit, illustrated in Fig. 7.

This unit is also where the power line attaches, allowing the three lines to follow the movement of the kite in the wind window, passively rotating within a range from −135 to +135° around the vertical axis. This azimuth rotation is measured by an angle sensor. The power line is connected to the rotating head via a universal joint that allows a rotation of 90° around the horizontal axis and a rotation of ±45° around the swivel axis, measured by additional angle sensors. Assuming fully tensioned lines and concatenating the three successive azimuth, elevation and swivel rotations, the position of the wing in the wind window can be determined. The forces in the steering and power lines are measured with load cells. It is important to note that because of the additional swivel rotation, the elevation and azimuth angles recorded by the pivot unit do not correspond to the equally denoted angular coordinates β and ϕ used in Sect. 2.1 and 2.2.

Figure 8 Components of the kite sensor unit (Elfert, 2021). The Teensy 3.6 microcontroller is not visible, as it is installed on the lower board.

A weather station is mounted on the roof of the towing vehicle to document the test conditions and set the desired simulated wind velocity. The included cup anemometer and wind vane measure the magnitude and direction of the relative flow velocity generated by the towing. To avoid disturbances from the vehicle itself, the weather station is mounted on a tripod approximately 1 m above the roof. The weather station also measures the temperature, air pressure and humidity, and it is the only sensor system operating at a measurement frequency of only 1 Hz. All other data are acquired at a frequency of 50 Hz.

3.2 Measuring kite position, velocity and orientation

The sensor system consists of the kite sensor unit, shown in Fig. 8, and a base sensor unit mounted on the test bench.

The data acquired by the kite sensor unit are transmitted wirelessly to the base sensor unit which, together with its own data, transmits these further to the test bench computer. The hardware components of the kite and base sensor units are largely identical and listed in Table 1.

PJRC, 2020InvenSense, 2020Digi, 2020Mediatek, 2024NXP, 2020

Table 1 Hardware components of the kite sensor unit.

Using GNSS sensors for position measurement of fast-flying kites on short lines is challenging, as frequently reported in the literature (Fagiano et al., 2013a, b; Erhard and Strauch, 2013a). Within the frame of this project, it was considered that at least the GNSS data of the base sensor unit would be of great added value for the subsequent data analysis. For example, it is helpful for a plausibility check to know what kind of route was followed on the airfield or at which point on the airfield certain measurement data were recorded. Since the kite sensor unit and the base sensor unit were to be built identically anyway to reduce complexity and no disadvantage was to be expected by integrating the GNSS into the kite sensor unit in any case, the GNSS module was also mounted on the board of the kite sensor unit.

The inertial measurement unit (IMU) data were post-processed with a fusion algorithm developed by Seel and Ruppin (2017). The settings of this algorithm have a direct physical meaning, representing the half-life period of the corresponding correction in seconds. In contrast to most IMU sensor fusion algorithms, it is possible to set separate weights for gravity-based and magnetic-field-based estimation. Thus, for example, the negative influence of a magnetic field disturbed by external influences on the orientation estimation can be reduced. Another special feature is an adaptive weighting of the influence of the measurement data of the acceleration sensors, which depends on the dynamics.

An alternative fusion algorithm was developed by Freter et al. (2020) to improve the kite position estimate. This is because a high-quality position estimate is a pre-condition for a good yaw angle estimate. The algorithm fuses the high-frequency and delay-free IMU data with the measured line angles, which allows for compensation of the inertia and sag of the lines. At the same time, accurate measurement data of the line angle sensors serve as a reference to counteract the drift behaviour of the IMU estimation. Since the IMU measures in the kite-fixed reference frame, while the line angle sensors measure in the test-bench-fixed reference frame, a coordinate transformation must be performed for a meaningful fusion. The algorithm of Freter et al. (2020) already includes a transformation from the kite's body-fixed reference frame to an Earth-fixed SEU reference frame (see Fig. 4). When assuming, for simplicity, that the test bench moves in a perfectly horizontal plane, the bench-fixed reference frame differs from the SEU reference frame only by a rotation with angle Π around the vertical axis. This angle can be calculated, for example, from the GNSS or IMU data of the base sensor unit, as shown in Fig. 9.

Figure 9 Kite-fixed coordinate system and test-bench-fixed coordinate system (Elfert, 2021).

3.3 Measuring relative flow velocity at the kite

The inflow velocity vector at the kite was measured with a custom-developed, low-cost five-hole Prandtl probe. A differential pressure flow meter is fairly accurate over a large measurement range compared to other techniques and accounts for varying air density. Avoiding any moving parts, it can be designed to be reliable and robust. The developed probe is compact and lightweight, and its low inertia reduces the influence on the flight behaviour of the kite. The main disadvantage is the high cost of commercial multi-hole Prandtl probes. To accurately measure the free-stream flow velocity, the pressure openings of the probe must be positioned as far upstream of the kite's leading edge as possible, which means that the system is prone to being damaged in the event of a crash. For this reason, a low replacement cost for the probe was one of the key requirements for the development. Another challenge was that both the expected maximum values and the range of flow velocities are low in this application compared to the conventional application areas of such probes, such as aviation or racing. The Prandtl probe can be attached to the kite sensor unit and mounted together to the kite's central strut, as shown in Fig. 10.

Figure 10 Onboard sensor system with the Prandtl probe mounted on the kite (Elfert, 2021).

The orientation of the probe can be adjusted by exchanging the triangular adapter between the housing and the probe. This is adjusted in between flight tests so that the probe is aligned as much as possible with the inflow when in a non-manoeuvring flight. It should be mentioned that the angle of attack of the kite cannot be directly deduced from the measured angle of attack of the probe. For this, at least the probe's orientation with respect to a defined reference orientation on the kite must be known. In the case of fixed wings, this reference is typically the chord. However, kites deform strongly due to the actuation of the bridle line system and under the influence of aerodynamic loads, so a constant chord cannot be assumed, and thus at most a local angle of attack can be measured. Because the sensor system is mounted to the central strut tube, only the orientation of the probe or the inflow vector with respect to this part of the kite can be determined with certainty.

All necessary calculations to determine the magnitude and orientation of the inflow vector from the raw data of the differential pressure sensors are performed in the microcontroller of the kite sensor unit. Three differential pressures are calculated from the raw data of the probe: the differential pressure of the centre hole to the holes for static pressure measurement and the differential pressure of each of the two opposite holes for the angle of attack and the sideslip angle. Using these, two non-dimensional coefficients are calculated, which are unique for a given orientation of the inflow vector and independent of the vector magnitude. To determine the angle of attack and the sideslip angle from these coefficients, we created a look-up table from wind tunnel experiments in which we adjusted the probe's orientation relative to the flow.

The measured centre pressure difference starts to deviate from the dynamic pressure at angles of incidence of more than 10°. This happens because the holes for static pressure measurement are more and more in the incident flow, and the centre pressure hole is slowly rotated out of the incident flow. At 45°, this phenomenon becomes so strong that the differential pressures become negative. To calculate the actual dynamic pressure, the measured centre pressure difference is therefore scaled depending on the calculated flow angles. Scaling is also used to correct the pressure loss in the tubes, which depends on the inflow velocity and the tube length. The correction polynomial used for this is determined from the measurement data measured in the wind tunnel at different incident flow velocities for a flow-aligned probe.

4 Data acquisition and analysis

In the following, the flight control algorithm developed specifically for this project and the post-processing of the raw data are presented in more detail.

4.1 Control algorithm for robust automated flight manoeuvres

The purpose of the flight controller is to ensure reproducible figure-eight manoeuvres in a wind environment with disturbances, such as turbulence and gusts. Our aim was to develop an algorithm that requires no a priori parameter knowledge of the kite. It should further be possible to intuitively adjust the shape of the figures via the controller parameters. Fagiano et al. (2014) proposed an algorithm that fulfils these requirements, relying only on line angle sensor data. In this case, the controlled variable is the velocity angle of the kite, defined as the angle between the kite velocity vector and a fixed reference vector.

The selected algorithm generates the figure-eight path by alternatingly switching between two different target points P₊ and P₋, as illustrated in Fig. 11 and presented in more detail in Lange (2018). We decided to fly the kite upwards during the turning manoeuvres because the probability of crashes during these “up loops” is lower than during the alternative “down loops”.

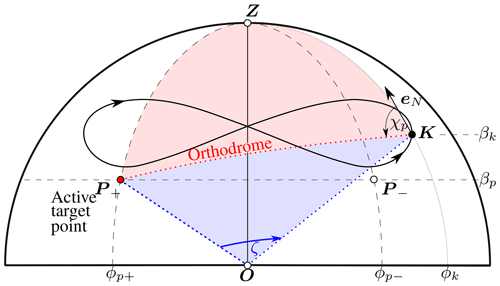
Figure 11 Calculation of the required course angle using the orthodrome, adapted from Fagiano et al. (2014) and Lange (2018).

The target points are switched before they are reached. To enforce that the kite flies “up loops” after switching the target point, it is forced to turn towards the zenith. The course angle χ_p required to reach the active target point P is determined from the current position of the kite using nautical course angle calculation. In contrast to Fagiano's original algorithm, the course is not calculated using the rhumb lines but the orthodromes. Initial field tests showed that this modification can lead to smoother and more robust flight manoeuvres. Using the orthodromes, the sphericity of the kite's surface of motion is taken into account, which Fagiano et al. (2014) did not do.

The shortest distance on the spherical surface between the kite K and the target point P is given by the great circle arc, denoted as orthodrome and indicated by the dotted red line in Fig. 11. For a unit sphere, the length of the orthodrome is numerically equal to the angle ζ spanned by the radial lines to the two points on the surface. In Fig. 11, the respective great circle sector is shaded in blue. The angle ζ can be derived from the law of cosines for the shaded red spherical triangle spanned by points K, P and Z on the unit sphere with the corresponding opposite sides 90^°−β_p, 90°−β_k and ζ. The formulation for the angle ϕ_p−ϕ_k with opposite side ζ leads to (Gellert et al., 1975)

$$\begin{array}{}\text{(14)}& \cos \mathit{\zeta }=\sin {\mathit{\beta }}_{\mathrm{k}}\sin {\mathit{\beta }}_{\mathrm{p}}+\cos {\mathit{\beta }}_{\mathrm{k}}\cos {\mathit{\beta }}_{\mathrm{p}}\cos \left({\mathit{\varphi }}_{\mathrm{p}}-{\mathit{\varphi }}_{\mathrm{k}}\right).\end{array}$$

Similarly, the formulation for the initial course angle χ_p with opposite triangle side 90°−β_p leads to

$$\begin{array}{}\text{(15)}& \cos {\mathit{\chi }}_{\mathrm{p}}={\displaystyle \frac{\sin {\mathit{\beta }}_{\mathrm{p}}-\sin {\mathit{\beta }}_{\mathrm{k}}\cos \mathit{\zeta }}{\cos {\mathit{\beta }}_{\mathrm{k}}\sin \mathit{\zeta }}}.\end{array}$$

Using this initial value, the set point is defined as (Fagiano et al., 2014)

$$\begin{array}{}\text{(16)}& {\mathit{\gamma }}_{\mathrm{p}}=\left\{\begin{array}{cl}{\mathit{\chi }}_{\mathrm{p}},& \mathrm{for}{\mathit{\varphi }}_{\mathrm{k}}\le {\mathit{\varphi }}_{\mathrm{p}\pm },\\ {\mathit{\chi }}_{\mathrm{p}},& \mathrm{for}{\mathit{\varphi }}_{\mathrm{k}}>{\mathit{\varphi }}_{\mathrm{p}\pm }\end{array}\right..\end{array}$$

Because the switching between target points leads to abrupt changes in the reference variable, a low-pass filter is connected downstream, which softens these jumps of the target heading angle before it is transferred to the inner loop of the controller. In this way, a steady evolution of the reference variable is achieved, and the rate of change is adapted to the inherent dynamics of the kite. A block diagram of the cascaded velocity angle controller is shown in Fig. 12.

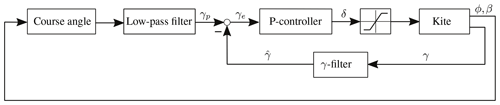
Figure 12 Block diagram of the velocity angle controller, adapted from Fagiano et al. (2014).

Figure 13 Typical time-dependent contributions to the left- and right-hand side of Eq. (17) between two U-turns of the towing vehicle (Elfert, 2021).

In the inner loop, the feedback of the control deviation takes place via a simple proportional controller (P-controller). A manipulated variable limitation occurs in the downstream saturation block following the P-controller. The current velocity angle of the kite required for calculating the control deviation is calculated from Eq. (5). The velocity angle is thus defined in a range of χ∈[−180, 180°]. This can cause erroneous calculations in the form of jumps during the velocity angle. In certain flight situations, for example, when the kite is held steady in the zenith, the kite can fly backwards in the wind direction for a short time. In this case, the value of the velocity angle would jump from 0 to 180 or −180°. The noise of the line angle sensors can lead to similar misinterpretations. To prevent such physically impossible jumps in the trajectory of the kite, an additional filter is used. The size and robustness of the eight-shaped trajectories generated with this algorithm can be influenced by shifting the target points, the choice of the gain factor and the setting of the low-pass filter.

4.2 Measurement data analysis

The steering gain and dead time were determined using a rearranged version of Eq. (13):

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{\dot{\mathit{\psi }}\left(t\right)}{v_{\mathrm{a}}\left(t\right)}}=g_{\mathrm{k}}\mathit{\delta }(t-d).\end{array}$$

The time-dependent left-hand side of this equation differs from the time-dependent steering input δ(t) on the right-hand side only by a scaling factor g_k and a time delay d, both of which we assume to be functions of the power setting of the kite. Figure 13 illustrates two typical signals recorded during the towing on the straight track between two U-turns.

In this particular example, 10 manoeuvres were performed between the two turning points. The steering gain and dead time can be determined from the two time-dependent signals by numerical optimization, fitting the right-hand side of Eq. (17) for the considered measurement period as closely as possible to the left-hand side. For this purpose, we used a simplex method with a maximum likelihood estimation (MLE).

The data analysis for a specific power setting is illustrated schematically in Fig. 14.

Figure 14 Data analysis for flight manoeuvres with identical power settings, adapted from Elfert (2021).

Especially at low power settings, the kite needed some time to settle in and converge to uniform flight manoeuvres. The data available from different measurements were cropped off at the start to remove the effects of these transient start-up phases. To minimize the effect of random disturbances, the data subsets were kept as large as possible, cropping them at the end to the same size. The MLE was then applied to each subset to determine the respective steering gain and dead time. Of these, the mean values were finally calculated as representative of the specific power setting of the kite.

5 Experimental results

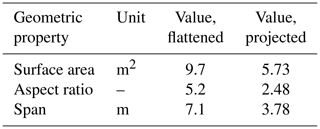
The measurements were conducted on 15 September 2020 at the former airfield in Pütnitz, Germany, using a Vegas 2015 kite from Duotone Kiteboarding (formerly North Kiteboarding) with a flattened wing surface area of approximately 10 m². Figure 15 shows the kite with a mounted Prandtl tube.

Figure 15 The Vegas 2015 kite with mounted Prandtl tube, adapted from Elfert (2021).

The design geometry is summarized in Table 2.

Table 2 Design geometry of the tested Vegas 2015 kite (values taken from the largely similar 2018 model).

During the measurement runs the ambient wind speed $v_{\mathrm{w}}^{\mathrm{0}}$ was generally up to 3 m s⁻¹, while some rare wind gusts would occasionally increase this to 5.8 m s⁻¹. For all measurements, the simulated wind speed v_w was set by the towing vehicle's driving speed $v_{\mathrm{b}}^{\mathrm{0}}=\mathrm{11.3}$ m s⁻¹ (22 kn). This specific speed was chosen because it is the median of the suitable wind speed range specified by the manufacturer. It can thus be assumed that the aerodynamic loading and the respective flight behaviour are well within the range for which the kite was designed.

The maximum length difference between power and steering lines was $\mathrm{\Delta }{l}_{\mathrm{PL},\max }=\mathrm{500}$ mm. The power range for which the kites were designed is in fact more narrow, meaning that we were also able to analyse off-design actuation scenarios with a very low power setting. In these cases, we observed that the steering lines were sagging so much that even the maximum steering input would only straighten the lines without actually actuating the wing, leaving it unresponsive to the control input. At slightly higher power settings, it was possible to generate a small yaw movement with maximum steering input, but this was insufficient for controlled figure-eight flight manoeuvres.

For this reason, we first had to iteratively determine the lowest feasible power setting before conducting any measurement runs. Then, the target points and the controller gain factor had to be adjusted until it was possible to fly uniform and sufficiently robust manoeuvres. For the kite used, a minimum power setting of u_p=0.4 was determined.

Figure 16 Steering gain g_k and dead time d as functions of the power setting u_p for the kite Vegas 2015 with a 10 m² wing surface area. Adapted from Elfert (2021).

5.1 Steering gain and dead time

Following the procedure outlined in Sect. 2.3, the entire range of power settings of the kite was covered with a single measurement run by increasing the power setting by Δu_p=0.1 at every second U-turn, starting at the lower limit u_p=0.4 until reaching the fully powered state at u_p=1. Consequently, every tow direction was measured once per power setting. As described in Sect. 4.2, a data window of fixed size was used for the analysis between two turning points, resulting in one window per power setting and tow direction. We found the measurement cycles 1000 to 3500 to span a suitable data range, excluding the transient start-up phases. Because the power setting affects the aerodynamic properties and with that also the flight speed of the kite (Hummel et al., 2019), the number of figure-eight manoeuvres per data window varied with the power setting.

Figure 16 shows the resulting average steering gain and dead time as functions of the power setting for the first measurement run.

The expected increase in the kite's agility with the power setting is evident from the pronounced monotonic increase in the steering gain and decreased dead time. The higher the power setting, the faster and stronger the reaction of the kite is to control inputs. The main source of experimental uncertainty was estimating the yaw angle ψ using the fusion algorithm described in Sect. 3.2. Additional uncertainty was introduced by the use of numerical optimization, which is part of the MLE algorithm described in Sect. 4.2.

5.2 Sensitivity analysis

Several sensitivity analyses and plausibility checks were conducted to increase confidence in the experimental results. We first assessed the influence of the initial values on the optimization result of the MLE, finding a significant effect only for strong deviations from realistic initial values. This observation is illustrated in Fig. 17, where the red line resulted from reasonable initial values $g_{\mathrm{k},\mathrm{0}}=\mathrm{0.3}$ rad m⁻¹ and d₀=600 ms, and the blue line resulted from extreme initial values $g_{\mathrm{k},\mathrm{0}}=\mathrm{10}$ rad m⁻¹ and d₀=1200 ms. It is evident that the red line follows the noisy raw signal $\dot{\mathit{\psi }}/v_{\mathrm{a}}$ more closely in magnitude and phase shift.

Figure 17 MLE optimization with reasonable (red) and extreme (blue) initial values, adapted from Elfert (2021).

Figure 16 shows that the calculated turning characteristics vary slightly for the two tow directions: 250 and 70°. Suspecting that this was caused by variations in the inflow velocity due to ambient wind or thermals, we conducted a sensitivity analysis to assess the influence of such variations. As a first step, the plausibility of the inflow velocity measurements was investigated because the measurement campaign was in fact the first occasion that the custom-developed Prandtl probe was used in field tests. The inflow speed was checked by stopping the crosswind flight manoeuvres, i.e. setting v_k in Eq. (4) to 0 and towing the kite in a static flight position relative to the vehicle. The inflow speed measured in this flight mode was roughly 1 to 2 m s⁻¹ below the airspeed measured by the weather station on the towing vehicle.

The angle of attack and sideslip angle were checked by investigating the data of the first measurement run. Both diagrams in Fig. 18 include the manoeuvre release signal and the power setting, indicating when the kite was operated in automated figure-eight flight manoeuvres and at which power setting.

Figure 18 Inflow angle of attack α (a) and inflow sideslip angle β_s (b) at the Prandtl probe. Adapted from Elfert (2021).

Two manoeuvre releases are executed for each power setting step, corresponding to the two driving directions: 250 and 70°. As expected, the mean angle of attack decreases with increasing power setting.¹ It is also evident that the range of variation during crosswind flight increases with the power setting. This also holds for the sideslip angle, which, for power settings above 0.6 to 0.7, varies roughly between −15 and +15°. This range corresponds with what is known from previous studies on crosswind operations of kites (Ruppert, 2012; Fechner and Schmehl, 2018; Oehler and Schmehl, 2019).

Figure 19 compares the time histories of the sideslip angle and the yaw angle, showing a strong correlation and also an increasing range of variation of the yaw angle with the power setting. For a low power setting of 0.4, the yaw angle varies between −40 and +40°, which means the kite just sways left and right without completing any loop manoeuvres. For higher power settings, the range of variation increases but only occasionally reaches the extreme values −90 and +90°. Because a complete turning manoeuvre requires the yaw angle to vary by 180°, while the straight-path sections of a figure eight even expand this range by 10 to 30° in positive and negative directions, it is clear that even at higher power settings, the kite only sways left and right, rarely completing full loop manoeuvres. The main reason for this was the relatively high elevation angle (76–78°) during towing, which effectively depowers the kite and lowers its flight speed.

Figure 19 Inflow sideslip angle (red) at the Prandtl probe and yaw angle (green) of the kite calculated by the kite sensor unit. Adapted from Elfert (2021).

Figure 20 Inflow velocity measured at the Prandtl probe (green) and flight velocity (red) determined by the GNSS module. Tow speed set to $v_{\mathrm{b}}^{\mathrm{0}}=\mathrm{11.3}$ m s⁻¹. Adapted from Elfert (2021).

We also observed that contrary to expectations (see the discussion in Sect. 3.2), the kite-mounted GNSS module also worked reliably during highly dynamic flight manoeuvres. This can be seen in Fig. 20, where we compare the measured inflow velocity and the flight velocity determined by the GNSS module.

This “GNSS velocity” is measured in the Earth-fixed reference frame. From Eq. (4) it is clear that the GNSS velocity $v_{\mathrm{k}}^{\mathrm{0}}$ and the apparent wind speed v_a are identical for a vanishing ambient wind speed $v_{\mathrm{w}}^{\mathrm{0}}$. It is evident that the time history of the GNSS velocity closely follows the time history of the inflow velocity with only a small offset of around 2 to 3 m s⁻¹. The two velocities peak in the short breaks between the manoeuvre sequences. This increase is caused by the U-turns of the towing set-up, when the crosswind manoeuvres are discontinued, and the kite is positioned at the lateral edge of the wind window performing 180° turns at a substantially larger radius and correspondingly higher speed than the towing vehicle. The diagram also shows that the range of velocity fluctuations increases with the power setting.

Figure 21 Comparison of the steering gain g_k and dead time d averaged over both tow directions as functions of the power setting u_p for the Vegas 2015 kite with a 10 m² wing surface area when performing the MLE with the inflow velocity (blue) and GNSS velocity (red). Adapted from Elfert (2021).

5.3 Detection and correction of faulty data

The Prandtl probe and the kite-mounted GNSS sensor provide velocity data from two entirely different measurement techniques. The data can thus be combined to detect and correct faulty data, further reducing the uncertainty of the individual measurements. Figure 21 compares the mean turning performance g_k and mean dead time d calculated using either the inflow velocity or the GNSS velocity for the MLE algorithm.

The reported offset between the inflow and GNSS velocities leads to a steering gain offset Δg_k ranging from 0.01 to 0.04, affecting the mean values of the calculated turning performance in the form of an offset Δg_k ranging between 0.01 and 0.04. As expected, this offset does not significantly affect the calculated dead time.

The steering gains plotted in Fig. 16 for the two tow directions deviate most noticeably at the maximum power setting u_p=1. To determine whether this deviation was caused by the ambient wind velocity, the measured flow velocities were investigated in more detail. From Fig. 22, it can be seen that the time histories of the simulated wind velocity and the inflow velocity do not differ much between the two opposing tow directions. The small average velocity difference of roughly 1 m s⁻¹ does not explain the significant offset Δg_k of 0.03 (8.5 %) at the maximum power setting.

The actual cause for the offset of the steering gain can be traced back to the distinct peak of the inflow velocity in the last third of the second manoeuvre (tow direction 70°) illustrated in Fig. 22. An analysis of the position data showed that a cornfield about 3 m high was reached precisely at this point, which was the only landscape irregularity in the direct vicinity of the runway. Since high temperatures around 27 °C and cloudless skies prevailed on the day of the measurement campaign, it is reasonable to assume that the peak of the inflow value was caused by thermals above the cornfield. Because the simulated wind speed was measured by the weather station mounted on the roof of the vehicle and therefore much closer to the ground, this ambient wind field perturbation at the height of the kite does not show in the time history of the simulated wind speed.

Figure 22 Time histories of the simulated wind velocity measured by the weather station as well as the inflow velocity measured by the Prandtl probe during the last two manoeuvres in Fig. 20 with power setting u_p=1. Tow speed set to $v_{\mathrm{b}}^{\mathrm{0}}=\mathrm{11.3}$ m s⁻¹. Adapted from Elfert (2021).

A more detailed analysis of additional measurement channels revealed that the wind gust influenced the kite so strongly that the controller was thrown out of rhythm, not switching target points anymore (see Sect. 4.1). For high power settings, the controller gain factor was set to borderline aggressive and the sudden perturbation led to an overshoot of the controller so that the kite only oscillated around the right target point instead of alternating between the target points. Since the supervising pilot did not notice this anomaly in the video recording with the GoPro camera, the manoeuvre was not aborted, and the measurement data were accepted as valid and used for the post-processing. The steering gains g_k calculated with these data most likely turn out to be lower because the anomaly occurred close to the lateral edge of the wind window, where the inertia of the kite has a stronger effect on the steering behaviour. The examination of all manoeuvre runs of the first measurement run showed that the described faulty behaviour of the controller also occurred at the power settings u_p=0.9 and u_p=0.8. Just as with u_p=1, the error occurred exclusively in the 70° direction of travel and in the area of the cornfield. In contrast to u_p=1 and u_p=0.8, however, the error in u_p=0.9 does not have a noticeable effect on the calculated steering gain g_k. This can be explained by the fact that in this manoeuvre run the error did not occur directly at the edge of the cornfield but somewhat later so that the associated measurement data are no longer in the manoeuvre period selected for the evaluation.

To verify this hypothesis, the six manoeuvre runs of the three power settings concerned were evaluated separately using the measurement data of longer periods (manoeuvre cycle 1000 to 4500). Using these extended data, we could reproduce the described anomaly and the expected influence on the calculated steering gain g_k for the power setting u_p=0.9. Revisiting Fig. 16, it can thus be concluded that the steering gains derived from the measurement data of the 250° tow direction are of higher quality.

5.4 Second measurement run

Following the first measurement run, a second run was attempted. Unfortunately, incorrect initialization of the control algorithm led to an early crash of the kite, damaging the inflow measurement sensor so severely that on-site repair was not feasible anymore. A follow-up attempt led to another crash that damaged the remaining functionality of the kite sensor unit, so no further use of the onboard sensor system was possible. As a consequence, the second measurement run provided data only up to a power setting of u_p=0.7 and without inflow data. The Prandtl probe was not mounted in the second measurement run. The steering gain and the dead time were calculated from the GNSS velocity and are plotted in Fig. 23 with the corresponding data of the first measurement run. It is obvious that the kite behaviour differs substantially in the two runs.

Figure 23 Comparison of the mean values of steering gain g_k and dead time d averaged over both tow directions as functions of the power setting u_p for the Vegas 2015 kite with a 10 m² wing surface area when performing the MLE with the GNSS velocity. Adapted from Elfert (2021).

In the second run, the kite is overall more agile, reacting faster and more strongly to control inputs. The deviations can be explained by comparing the velocities and line forces during the two runs. The simulated wind and GNSS velocities of representative data sections are illustrated in Fig. 24.

Figure 24 Representative cut-outs of the simulated wind and GNSS velocity data during a period of equal length in the first (a) and second (b) measurement run. Tow speed set to $v_{\mathrm{b}}^{\mathrm{0}}=\mathrm{11.3}$ m s⁻¹. Adapted from Elfert (2021).

The mean values differ only slightly between the two runs, with the simulated wind velocity about 0.5 m s⁻¹ higher in the first run and the GNSS velocity about 0.3 m s⁻¹ higher in the second run. Using the GNSS velocity as a measure of the inflow speed, this difference would correspond to an approximate 6 % deviation in aerodynamic forces. However, the line forces plotted in Fig. 25 show that the mean force in the power line is about 30 % higher in the second run.

Figure 25 Representative cut-outs of the line force data during the periods shown in Fig. 24 in the first (a) and second (b) measurement run. Adapted from Elfert (2021).

With higher line tension, the kite reacts faster and more strongly to control input. The lower line forces in the first run can be explained by the stronger fluctuations of the simulated wind speed during the first run, as seen in Fig. 23. These fluctuations negatively impact the aerodynamic performance of the kite, thus decreasing the generated line forces. A thorough computational analysis of the effect of inflow turbulence on the energy harvesting performance of kites was presented in Fechner and Schmehl (2018).

Erhard and Strauch (2013b)Roullier (2020)Oehler et al. (2018)Erhard and Strauch (2013a)Cadalen et al. (2018)Oehler et al. (2018)Costello et al. (2018)

Table 3 Measured steering gain and dead time of kites, with and without a suspended kite control unit (KCU).

^* Flat, laid-out wing surface area.

5.5 Comparison with the literature

In the final step, we compared the measured turning behaviour with experimental results from the literature. In general, the definition of the steering input δ influences the calculated steering gain g_k. However, all studies with measured steering gain also included the steering input in a standardized way, allowing for a direct comparison of the measurements. Because of the linearity of the turn rate law, larger values of the maximum steering line length difference Δl_SL,max only lead to correspondingly larger amplitudes of the measured yaw angle change Δψ, not affecting the gain. Table 3 lists the results of other experimental studies together with our results.

The derivation of the turn rate law leading to Eq. (12) shows that the steering gain $g_{\mathrm{k}}=C/m$ implicitly includes a dependency on the surface-to-mass ratio of the kite because the constant C also includes the effective vertical wing surface area. Since the mass of a kite increases faster than its wing surface area, the steering gain generally decreases with the size of the kite. This is well reflected by the data in Table 3; however, it is also obvious that within a certain size interval, the type of kite and its specific design can also influence the turning behaviour substantially.

6 Conclusions

Compared to conventional aircraft, flexible membrane wings are highly manoeuvrable because of the low inertia and the entire canopy acting as a morphing aerodynamic control surface. The aim of the present study was to expand on an existing tow test set-up to systematically quantify this manoeuvrability. For this purpose, a control algorithm from the literature was adapted to operate the kite in automatic crosswind manoeuvres while towing it at constant speed along a straight runway. The widely used turn rate law was adopted to identify the steering gain and dead time from the measured flight dynamic response to a prescribed steering input. Towing the kite in concatenated back-and-forth loops made it possible to determine the manoeuvrability for the entire range of power settings within a single non-stop measurement run.

The results confirm the well-known behaviour of increasing agility with the power setting, as evidenced by increasing steering gain and decreasing dead time. An ambient wind speed leads to deviations for the two opposing tow directions. Generally, the larger the ambient wind speeds, the larger the differences are in steering behaviour. An extreme effect was observed during the first measurement run when a sudden peak in the inflow speed, potentially due to thermals above a neighbouring cornfield, triggered an anomaly of the flight controller, which, as it stayed undetected, led to a degraded measurement at the specific flight condition. Comparing the first and second measurement runs, the measurements also revealed a substantial impact of turbulent fluctuations of the simulated wind speed on the manoeuvrability of the wing. We concluded that an increasing degree of turbulence has a deteriorating influence on the flow around the wing, lowering the line forces and, in turn, the manoeuvrability.

A key finding of the present study is thus that the measurement quality crucially depends on the ambient wind conditions, which must be monitored closely. The experimental campaign revealed several practical limitations of the tow test set-up. Firstly, a Prandtl probe protruding from the wing's leading edge is a vulnerable high-precision instrument, especially when considering that flexible wings flying fast crosswind manoeuvres in a natural wind environment close to the ground are prone to occasional crashes. By design and nature, flexible wings cannot ensure rigorous flight stability as fixed-wing aircraft can. The loss of the probe and the entire onboard sensor module at the start of the second measurement run severely impaired the potential output of the measurement campaign. However, we also found that for sufficiently low ambient wind speeds, the flight velocity of the kite relative to the ground, denoted as GNSS velocity in the present work, can be used as a reliable indirect measure of the inflow velocity.

Secondly, operating a wing in crosswind manoeuvres greatly amplifies the pulling force. For safety purposes, we could tow only relatively small wings, flying these close to the edge of the wind window at relatively high elevation angles (around 70°) where complete figure-eight loops were often not feasible. For the larger kites used in airborne wind energy applications, it appears more adequate to identify the steering gain and dead time based on operational data in the original application setting with the fixed ground station. However, the effort to integrate a new kite design into the complete system hardware and control system can be considerable. Using the described set-up and procedure for tow tests of a scale model of the wing may be the more efficient way to evaluate new kite designs.