the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Analysis of control-oriented wake modeling tools using lidar field results
Jennifer Annoni
Paul Fleming
Andrew Scholbrock
Jason Roadman
Scott Dana
Christiane Adcock
Fernando Porte-Agel
Steffen Raach
Florian Haizmann
David Schlipf
The objective of this paper is to compare field data from a scanning lidar mounted on a turbine to control-oriented wind turbine wake models. The measurements were taken from the turbine nacelle looking downstream at the turbine wake. This field campaign was used to validate control-oriented tools used for wind plant control and optimization. The National Wind Technology Center in Golden, CO, conducted a demonstration of wake steering on a utility-scale turbine. In this campaign, the turbine was operated at various yaw misalignment set points, while a lidar mounted on the nacelle scanned five downstream distances. Primarily, this paper examines measurements taken at 2.35 diameters downstream of the turbine. The lidar measurements were combined with turbine data and measurements of the inflow made by a highly instrumented meteorological mast on-site. This paper presents a quantitative analysis of the lidar data compared to the control-oriented wake models used under different atmospheric conditions and turbine operation. These results show that good agreement is obtained between the lidar data and the models under these different conditions.
- Article
(1104 KB) - Full-text XML
- BibTeX
- EndNote
Wind plant control can be used to maximize the power production of a wind plant, reduce structural loads to increase the lifetime of turbines in a wind plant, and better integrate wind energy into the energy market (Boersma et al., 2017; Johnson and Thomas, 2009). Typically, wind turbines in a wind plant operate individually to maximize their own performance regardless of the impact of aerodynamic interactions on neighboring turbines. There is the potential to increase power and reduce overall structural loads by properly coordinating turbine control actions. Two common wind plant control strategies in the literature include wake steering and axial induction control. There has been a significant amount work done on wake steering, showing that this method has the most potential to increase power production (Annoni et al., 2015; Gebraad et al., 2016). Wake steering typically uses the yaw misalignment of the turbines to redirect the wake around downstream turbines. Various computational fluid dynamics simulations and wind tunnel experiments have shown that this method can increase power without substantially increasing turbine loads (Fleming et al., 2014; Gebraad et al., 2016; Jiménez et al., 2010). Yaw-based wake steering control has also been used in optimization studies of turbine layouts to improve the annual energy production of a wind plant (Fleming et al., 2016; Stanley et al., 2017; Thomas et al., 2015). Recent computational fluid dynamics (CFD) studies have determined that the shape of the wake and atmospheric stability are significant factors in wake steering (Vollmer et al., 2016).
Control-oriented models are essential for developing and deploying wake steering strategies in wind farms. In particular, control-oriented models can be used in an open loop whereby a lookup table is generated a priori and used in the field. Alternatively, due to its computational efficiency, a control-oriented model can be used to perform online optimization with feedback to adjust to changing conditions in the atmosphere or wind farm, e.g., turbine down for maintenance. Lastly, control-oriented models are also useful for large-scale analysis and assessing the impact of controls and optimization on annual energy production. Overall, these models are critical to the success of wind farm controllers and, as a result, full-scale validation of these control-oriented models is essential and a high priority in this area of research.
A full-scale demonstration of wake steering is necessary to understand the benefits of wake steering and to validate the benefits predicted by simulations. Wind tunnel tests have been conducted that show encouraging results that match simulation results based on wake redirection (Campagnolo et al., 2016; Schottler et al., 2016). In addition, there are preliminary results of the benefits of wake steering from an offshore commercial wind plant (Fleming et al., 2017b). The National Wind Technology Center also conducted a detailed full-scale demonstration in which a utility-scale turbine operated at various yaw offsets while the wake was measured using a scanning lidar. In this paper, the lidar data collected from this campaign are used to validate control-oriented tools that are used for wind plant control. The main contributions of this work include a review of control-oriented models used for wake steering as well as a quantitative analysis of these models with respect to full-scale lidar results. The results between the wake models and lidar data show good agreement under various atmospheric and turbine operating conditions, as shown in Sect. 4. This is an encouraging result that provides confidence in previously reported benefits of wake steering. The wind plant control tools, including wake models, turbine models, and lidar models, used in wind plant controls are introduced in Sect. 2. The field campaign is briefly introduced in Sect. 3. Finally, Sect. 5 provides conclusions and discusses future work.
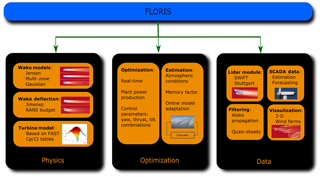
FLORIS is defined as a set of control and optimization tools used for wind farm control developed at the National Renewable Energy Laboratory and TU Delft; see Fig. 1. This tool models the turbine interactions in a wind plant and can be used to perform real-time optimizations to improve wind plant performance and integrate SCADA data collected at wind plants. This section focuses on the wake models, turbine models, and the lidar module used in this paper.
2.1 Wake model
The wake models available in FLORIS include the Jensen model (Jensen, 1983), the FLORIS wake model (Gebraad et al., 2016), and the self-similar wake model with contributions from Bastankhah and Porté-Agel (2014, 2016), Abkar and Porté-Agel (2015), Niayifar and Porté-Agel (2015), and Dilip and Porté-Agel (2017). Although only these three models are addressed, any wake model can be substituted into this framework. This paper also demonstrates the modular framework for FLORIS and will address the benefits of adding complexity to wake models used to characterize the aerodynamic interactions between turbines.
2.1.1 Jensen model
The Jensen model has been used for numerous studies on wind plant controls (Jensen, 1983; Johnson et al., 2006; Katic et al., 1986). This model has a low computational cost due to its simplicity and is based on assumptions that there is a steady inflow, linear wake expansion, and the velocity in the wake is uniform at a cross section downstream. The turbine is modeled as an actuator disk with uniform axial loading in a steady uniform flow.
Consider the example of a turbine operating in free-stream velocity, U∞. The diameter of the turbine rotor plane is denoted by D and the turbine is assumed to be operating at an induction factor, a. A cylindrical coordinate system is placed at the rotor hub of the first turbine with the streamwise and radial distances denoted by x and r, respectively. The velocity profile at a location (x,r) is computed as
where the velocity deficit, δu, is given by
In this model, the velocity, u, is defined in the axial (x) direction and the remaining velocity components are neglected. The wake is parameterized by a tuneable nondimensional wake decay constant, k. Typical values of k range from 0.01 to 0.5 depending on ambient turbulence, topographical effects, and turbine operation. For example, if the ambient turbulence is high, then the wakes within the wind farm will recover faster due to the mixing of the wake. As a result, the k value will be higher, indicating that the wake will recover faster. There is no standard rule for how k varies with turbulence intensity.
Limitations
The Park model can be used to compute the power production and velocity deficit of a turbine array. This is useful in determining the operating conditions of a wind farm to maximize power. However, it has no notion of added turbulence in the downstream wake due to varying turbine operation. The assumptions are based on a steady inflow acting on an actuator disk with uniform axial loading and as noted in Frandsen et al. (2006); the Jensen model does not conserve momentum. Despite its limitations, the Jensen model can be computed in fractions of a second and can provide some insight into turbine interaction that can be used to understand the results obtained from higher-fidelity models. In addition, if uncertainty is included, the Jensen model performs well and predicts wake interactions well under normal operating conditions.
2.1.2 Multi-zone
The multi-zone model, developed in Gebraad and Van Wingerden (2014), is a modification of the Jensen model described in the previous section. Modifications were made to better model the wake velocity profile and effects of partial wake overlap, especially in yawed conditions. The multi-zone model defines three wake zones, q: (1) near-wake zone, (2) far-wake zone, and (3) mixing-wake zone. The effective velocity at the downstream turbine i is found by combining the effects of each of the wake zones of the upstream turbine j:
where Xi is the x location of turbine i, is the overlap area of a wake zone, q of a turbine i with the rotor of turbine j, and ci,q(x) is a coefficient that defines the recovery of a zone q to the free-stream conditions.
where mU,q is defined as
for corresponding to the three wake overlap zones, where aU and bU represents tuned model parameters, Di is the rotor diameter of turbine i, γi is the yaw offset of turbine i, and MU,q are tuned scaling factors that ensure that the velocity in the outer zones of the wake will recover to the free-stream conditions faster than the inner zone. The parameters of the model were tuned to match the results from high-fidelity wake simulations (Gebraad et al., 2016). The most influential parameter is ke because it defines both wake expansion and wake recovery. Additional details can be found in Gebraad et al. (2016).
Limitations
The multi-zone model was developed, in comparison with high-fidelity models, to characterize turbine interactions when turbines were operating in partial wake or yawed conditions. The multi-zone model is a computationally inexpensive model that is suitable for control and optimization studies to improve wind plant performance. However, there are 13 free parameters that can be tuned in this model and the tuning can be sensitive depending on the parameters chosen to tune. Like the Jensen model, this model does not have any sensitivity to turbulence intensity or added turbulence generated by an upstream turbine and does not explicitly conserve momentum.
2.1.3 Gaussian model
Lastly, a Gaussian model is incorporated in the overall FLORIS wake modeling and control tools. This model was introduced by several recent papers including Abkar and Porté-Agel (2015), Bastankhah and Porté-Agel (2014, 2016), Niayifar and Porté-Agel (2015), and Dilip and Porté-Agel (2017). This model includes a Gaussian wake to describe the velocity deficit, added turbulence based on turbine operation, and atmospheric stability.
Velocity deficit
The velocity deficit of a wake is computed by assuming a Gaussian wake, which is based on self-similarity theory often used in free shear flows, (Pope, 2000). An analytical expression for the three-dimensional velocity deficit behind a turbine in the far wake can be derived from the simplified Navier–Stokes equations as
where C is the velocity deficit at the wake center, δ is the wake deflection (see Sect. 2.2), zh is the hub height of the turbine, σy defines the wake width in the y direction, and σz defines the wake width in the z direction. Each of these parameters are defined with respect to turbine i; subscripts are excluded for brevity. The subscript “0” refers to the initial values at the start of the far wake, which is dependent on ambient turbulence intensity, I0, and the thrust coefficient, CT. For additional details on near-wake calculations, the reader is referred to Bastankhah and Porté-Agel (2016). Abkar and Porté-Agel (2015) demonstrate that σy and σz grow at different rates based on lateral wake meandering (y direction) and vertical wake meandering (z direction). The velocity distributions σz and σy are defined as
where ky defines the wake expansion in the lateral direction and kz defines the wake expansion in the vertical direction. For this study, ky and kz are set to be equal and the wake expands at the same rate in the lateral and vertical directions. The wakes are combined using the traditional sum of squares method (Katic et al., 1986), although alternate methods are proposed in Niayifar and Porté-Agel (2015).
Atmospheric stability
This model also accounts for physical atmospheric quantities such as shear, veer, and changes in turbulence intensity (Abkar and Porté-Agel, 2015; Niayifar and Porté-Agel, 2015). Shear, veer, and turbulence intensity measurements are typically available in field measurements and will be used to characterize atmospheric stability in this particular model. It should be noted that these three parameters do not sufficiently characterize atmospheric stability as defined in Stull (2012). Other parameters such as vertical flux and temperature profiles are necessary to fully capture atmospheric stability.
This model is a three-dimensional wake model that includes shear by using the power log law of wind:
where αs is the shear coefficient and Uinit indicates the initial flow field. A high shear coefficient, αs>0.2, is typically used for stable conditions and a low shear coefficient, αs<0.2, is typically used for unstable conditions (Stull, 2012).
This wake model also takes into account veer associated with wind direction change across the rotor. A rotation factor is added to the Gaussian wake (Eq. 6) such that
where ϕ is the amount of veer across the rotor when this equation represents a standard Gaussian rotation.
Lastly, turbulence intensity is accounted for in the model by linking ambient turbulence intensity to wake expansion. An empirical relationship is provided in Niayifar and Porté-Agel (2015):
where I represents the turbulence intensity, and ka and kb are tuning parameters where ka=0.38371 and kb=0.003678 in Niayifar and Porté-Agel (2015). As stated previously, ky and kz will be set equal in this study.
Added turbulence
This wake model also computes added turbulence generated by turbine operation and ambient turbulence conditions. For example, if a turbine is operating at a higher thrust, this will cause the wake to recover faster. Conversely, if a turbine is operating at a lower thrust, this will cause the wake to recover slower. Conventional linear flow models have a single wake expansion parameter that does not change under various turbine operating conditions. Niayifar and Porté-Agel (2015) provided a model that incorporated added turbulence due to turbine operation:
where N is the number of turbines influencing the downstream turbines, I0 is the ambient turbulence intensity, and the added turbulence due to turbine i, , is computed as
where I0 is the ambient turbulence intensity and a is the axial induction factor of the turbine, which can be defined in terms of CT based on Burton et al. (2001) and Bastankhah and Porté-Agel (2016):
In Niayifar and Porté-Agel (2015), the number of turbines, N, used to determine the added turbulence is N=1. In this formulation, N is determined based on a predefined distance to the downstream turbine rather than only including the influence of one turbine. For example, this model considers contributions to the added turbulence intensity from turbines within 15D. This has been shown to be beneficial, especially with closely spaced turbines. Studies have shown that the added turbulence intensity has reached an equilibrium point between two and three turbines downstream (Chamorro and Porté-Agel, 2011).
Limitations
This wake model is an analytical model with approximations made from the steady-state Navier–Stokes equations based on free shear flows. In addition, unlike the previous two models, this model conserves momentum. However, it relies on a linear wake expansion model and has six tuning parameters based on empirical relationships for wake expansion and turbulence intensity (Eqs. 11 and 13). The main benefits of this model come from the ties to physical measurements in the field such as shear, veer, and turbulence intensity and its roots in free shear flow theory.
2.2 Wake deflection
The wake models defined above include wake deflection models that approximate the amount of lateral movement based on the yaw misalignment of the turbine. Two wake deflection models are defined in the FLORIS wind plant modeling and control framework and are briefly described in this section.
2.2.1 Jimenez model
An empirical formulation was presented in Jiménez et al. (2010) and used in the multi-zone formulation (Gebraad et al., 2016). When a turbine is yawed, it exerts a force on the flow that causes the wake to deflect and deform in a particular direction. The angle at the wake centerline is defined as
where ξinit is the initial skew angle from the wake centerline and kd is a tuneable deflection parameter. In Gebraad et al. (2016), the wake deflection angle is integrated to determine the amount of deflection, δ, achieved by yaw misalignment in the spanwise (y) direction:
The deflection, δ, is achieved by integrating a second-order Taylor series approximation as shown in Gebraad et al. (2016).
2.2.2 Bastankhah model
In Bastankhah and Porté-Agel (2016), wake deflection due to the yaw misalignment of turbines is defined by performing a budget analysis on the Reynolds-averaged Navier–Stokes equations. The wake deflection angle at the rotor is defined by
and the initial wake deflection, δ0, is defined as
where x0 is the length of the near wake as defined in Bastankhah and Porté-Agel (2016). The total deflection of the wake due to wake steering is defined as
where . Expressions for the other symbols in the above equation are provided in Sect. 2.1.5. See Bastankhah and Porté-Agel (2016) for details on the derivation.
2.2.3 Wake asymmetry
Wake deflection is known to be asymmetric based on the sign of the yaw misalignment. In particular, positive yaw angles are more effective than negative yaw angles (Fleming et al., 2018). Previously, it was speculated that there was a rotation-induced lateral offset that is caused by the interaction of the wake rotation with the shear layer (Gebraad et al., 2016). An empirical correction used to account for asymmetry is presented in Gebraad et al. (2016).
Fleming et al. (2018) propose that there is an asymmetry in the wake that can be described by counter-rotating vortices, turbine rotation, and shear rather than actual deflection. Updates to the FLORIS wake modeling framework to reflect the asymmetry will be done in future work.
2.3 Turbine model
In addition to wake modeling tools, a turbine model is used in the wind plant tools to provide a realistic description of turbine interactions in a wind plant. The turbine model consists of a CP∕CT table based on wind speed and constant blade pitch angle generated by FAST (Jonkman, 2010). The coupling between CP and CT is critical in understanding the benefits of wind plant controls. CP and CT can also be coupled using actuator disk theory, which is based on the turbine operation defined by an axial induction factor, a:
It is important to note that CP and CT values are used that correspond to the local conditions each turbine is operating in. For example, a turbine operating in a wake has a different CP∕CT than a turbine operating in free-stream conditions.
The steady-state power of each turbine under yaw misalignment conditions is given by Gebraad et al. (2016):
where p is a tuneable parameter that matches the power loss due to yaw misalignment seen in simulations. In actuator disk theory (Burton et al., 2001), p=3. However, based on large-eddy simulations, the turbine power in yaw misalignment has been shown to match the output when p=1.88 for the NREL 5 MW. Field observations run from p=1.4 (Fleming et al., 2017b) to p=2.2.
2.4 Lidar model
Finally, in this work a lidar model has been added to the FLORIS wind plant tools. This lidar model is based on the scanning lidar at the University of Stuttgart used in this study. This allows for direct comparison between lidar data collected by the scanning lidar and the wake model used. In particular, the scanning lidar used in the field campaign takes a weighted average of nine points along the line-of-sight trajectory. A lidar model is necessary to ensure this direct comparison. If any of the nine points are outside of the wake, the weighted average may lead to a more conservative estimate of the flow in the wake. More details on the lidar used in the wake steering campaign can be found in Raach et al. (2016, 2017) and Fleming et al. (2017a).
The velocity computed by the scanning lidar is based on a line-of-sight velocity. The lidar model used in the FLORIS framework computes the line-of-sight velocity, vLOS, in the same way that the lidar model computes the line-of-sight velocity so that each point scanned by the lidar can be compared directly to points computed by the wake model. The lidar computes a line-of-sight velocity for each point scanned. In particular, one scan point consists of Nweights weighted points that provide a robust velocity measurement at that location. In other words, Nweights points are used in a weighted sum to provide a robust velocity measurement at that scan point. The velocity at a single point can be computed as
where aj represents the weights assigned to each point, i indicates the scan point, and is the weighted sum of the measured velocity points . Typically the weights are assigned in a Gaussian manner.
Furthermore, the wind vector is projected onto the normalized laser vector point with a focus distance of and the resulting vLOS,i is
Additional details are provided in Raach et al. (2016). This model can be used in conjunction with the field data to perform closed-loop wind plant controls as is done in Raach et al. (2016). In addition, future work could use the simulated vLOS computed using this lidar model to fill gaps that are inevitably present in real-time lidar data.
A wake steering demonstration was conducted at the National Wind Technology Center using a utility-scale turbine. The utility-scale turbine operated at various yaw misalignment conditions and the resulting wake was continually recorded by a nacelle-mounted lidar. The campaign started in September 2016 and concluded in April 2017. This section describes the turbine, the meteorological tower used to record local conditions, and the lidar system mounted on the nacelle of the turbine. Details were first reported on the lidar field campaign in Fleming et al. (2017a). This paper expands the analysis and provides a quantitative comparison between the control-oriented models presented and the lidar data collected in this campaign.
3.1 Setup of the field campaign
The turbine used in this wake steering demonstration was the Department of Energy (DOE) 1.5 MW GE SLE turbine owned by the U.S. DOE and operated by the National Renewable Energy Laboratory. Details on the turbine are provided in Table 1.
The met tower is located 161 m upstream of the turbine in the predominant wind direction. The met tower was instrumented in accordance with IEC 61400-12-1. Table 2 lists the instrumentation used on the met tower. The turbine nacelle wind speed and wind direction are measured, recorded, and synchronized with the met tower data.
The lidar data are limited to a region in which the met tower is upstream of the turbine. The hub-height wind speed and wind direction measurements from the met tower are used to described the mean wind speed, wind direction, and turbulence intensity. The wind direction recorded at 38 and 87 m on the met tower is used to compute veer.
3.2 Lidar specifications
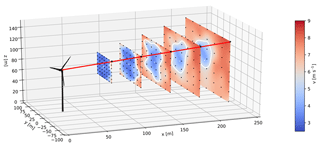
The University of Stuttgart scanning lidar system consists of two parts: (1) a WINDCUBE V1 from Leosphere and (2) a scanner unit developed at the University of Stuttgart. A two-degrees-of-freedom mirror is used for redirecting the beam to any position within the physical limitations of the mirror. The lidar can scan an area of 0.75D × 0.75D using up to 49 measurement points and five scan distances. The scan rate is dependent on the number of pulses used for each measurement position. The lidar system has been used for lidar-assisted control using inflow and wake measurements; see Raach et al. (2016).
The lidar scans a grid pattern seen in Fig. 2. The lidar is set to record a measurement point every 1 s and it scans five distances from 1D to 2.8D simultaneously. Each scan consists of 49 points and one scan takes 48 s on average. At each measurement point the lidar uses 10 000 laser pulses to measure the line-of-sight wind speed, vLOS, described in Sect. 2.4. Scans of similar atmospheric conditions and turbine operation are aggregated to produce a mean or median scan.
The results presented in this section show the comparison between the wake models described in Sect. 2 and the lidar data collected in the field campaign described Sect. 3. The results focus on comparisons of the velocity deficit behind the turbine, the wake deflection achieved in yaw misalignment conditions, and varying atmospheric conditions.
4.1 Data processing
It is important to note how the lidar data were processed for this study. The lidar data were first processed to filter out implausible data. Specifically, several methods were applied to check for hard-target measurements, filter out lidar data with a bad carrier-to-noise ratio, and check for plausibility of the measurement data. The data are also reduced through certain considerations, including (1) periods when the met tower is upstream of the turbine, (2) periods when the turbine is producing at least 100 kW, and (3) periods when the difference between the target and realized yaw misalignment is small. In particular, the instruments on the met tower that are used to measure wind speed and direction are more reliable when they are not operating in the wake of nearby turbines or in the wake of their own tower due to blockage effects. We also chose to only include data for which the turbine is operating normally. In this case, we define that as producing more than 100 kW. The turbine operation affects the wake properties and we need to ensure that we are comparing times when the turbine is performing as expected. Similarly, we only include times when the turbine yaw controller is tracking the specified offset within a few degrees to make a direct comparison with models.
4.2 Atmospheric conditions
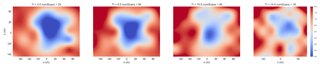
First, the lidar data collected in the field campaign were analyzed based on atmospheric conditions. In particular, turbulence intensity was examined to understand the behavior of each model under varying turbulence intensity conditions. Figure 3 shows the lidar scans at 180.95 m downstream (approximately 2.5D downstream). The turbulence intensity was computed for each lidar scan and separated into four bins with centers of 2 %, 6 %, 10 %, and 14 % with a wind speed of 8 m s−1. Figure 3 shows that the wake is strongest in low turbulence conditions and dissipates quickly in high turbulence conditions. This is consistent with previous work investigating the effects of atmospheric conditions on wakes (Smalikho et al., 2013). It is important to note that each image was generated with the maximum number of scans available after processing the data. More scans lead to a more robust measurement of the wake. A statistical analysis is presented in Fig. 4, which indicates the effects of the limited number of scans processed.
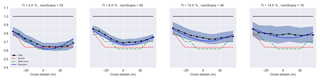
Figure 4Velocity deficit at 180.95 m downstream computed using lidar data, the Gaussian wake model, multi-zone wake model, and the Jensen wake model under different turbulence intensity conditions.
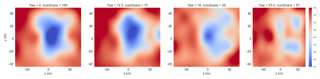
Figure 5Lidar data at 180.95 m downstream at different yaw misalignments ranging from 0 to 25∘. The title of each plot indicates the yaw angle and the number of scans used to produce each time-averaged figure.
Figure 4 shows how the control-oriented engineering models presented in this paper compare with the lidar data. The velocity deficit behind the turbine was computed by averaging the velocity across a “virtual” rotor and moving this rotor across the domain in the spanwise direction (shown in Vollmer et al., 2016). The bands indicate a 95 % confidence interval. A larger band indicates that fewer scans were processed. Each model was tuned to a subset of the lidar data, which included primarily low turbulence intensity data with a mean turbulence intensity of approximately 5 %. The values of each of the model parameters are shown in the Appendix. It is important to note that these values are tuned for the near wake due to the close proximity of the lidar scans to the turbine (2.35D). Although these measurements are near the turbine, the effects of turbulence intensity can still be observed along with wake deflection. Tuning the models appropriately with training data from this proximity, the models are able to perform reasonably well under varying atmospheric conditions and varying turbine operations even at these close proximities.
The Jensen and multi-zone wake models are shown to have good agreement in low turbulence scenarios; i.e., they fall within the confidence interval. This is expected as these models were tuned to low turbulence scenarios. However, when going to high turbulence intensity scenarios, they underpredict the velocity deficit significantly. This is because neither the Jensen nor the multi-zone model has turbulence intensity as an input to the model. The Gaussian model, however, is able to capture both low and high turbulence intensity scenarios; i.e., the model lies within the confidence interval bands under each turbulence scenario examined. This highlights the fact that, even under varying atmospheric conditions, the Gaussian model is able to accurately capture scenarios that it was not explicitly tuned for. The Jensen and multi-zone models can be retuned to fit high turbulence intensity data as well. Those values are also indicated in the Appendix.
4.3 Wake deflection
Wake deflection was also analyzed using the lidar data from this campaign. Figure 5 shows the wake deflection under turbine yaw misalignment observed by the scanning lidar at 180.95 m downstream. Under larger yaw angles, the wake deflects and deforms as has been reported in Howland et al. (2016) and Fleming et al. (2017b).
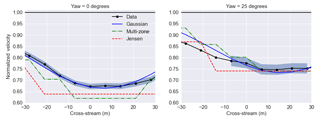
Figure 6Velocity deficit at 180.95 m downstream computed using lidar data, the Gaussian wake model, the multi-zone wake model, and the Jensen wake model under different yaw misalignment conditions.
Figure 6 shows the comparison of each control-oriented engineering model with the lidar data when the turbine is operating with no misalignment (left) and operating with 25∘ of yaw misalignment (right) at 180.95 m downstream, or approximately 2.5D downstream. Similar to Fig. 4, a “virtual” rotor is used to compute the effective wind speed at several spanwise locations. The data used in Fig. 6 include all turbulence intensity levels with wind speeds of 7–9 m s−1 when the turbine was operating with no misalignment and a yaw misalignment of 25∘. The average turbulence intensity is approximately 7 %. The data were aggregated and normalized over this range of wind speeds to include more scans and provide more robust statistics. The bands indicate a 95 % confidence interval.
Again, the Gaussian model is better able to predict the conditions at no misalignment (predicts velocities within the confidence intervals) since the multi-zone and Jensen models were both tuned to data with a lower turbulence intensity. When the turbine is operating in misaligned conditions, the turbine generates a cross-flow velocity component that is not captured by the lidar. This is because the lidar is operating on a rotating platform and does not reliably measure the wake on the left side due to this large cross-flow velocity component. As a result, only lidar data from −10 to 30 m are considered in the misaligned conditions. Under yaw-misaligned conditions, the Jensen, multi-zone, and Gaussian models all have good agreement with lidar data. In this case, the Jensen and multi-zone wake models have better agreement under yawed conditions than under normal conditions. One potential reason for this is that the “depth” of the wake is modified by the changing yaw angle; i.e., the thrust generated by the turbine is modified. This modified thrust is able to accommodate the underpredictions in the normal operating case. With more data, the analysis could be split into yaw misalignment conditions and turbulence intensity levels.
This paper compared field data from a scanning lidar measuring the wake of a turbine in normal operating conditions and yaw-misaligned conditions with control-oriented models. Validating these control models with field data in a variety of conditions is a critical step to implementing wind farm controls in the field. A quantitative analysis was done comparing the models in the FLORIS framework to these data. The data were processed to look at the effects of varying turbulence intensity levels as well as different yaw-misaligned conditions. The wake models used in the comparison included the Jensen model, the multi-zone model, and the Gaussian wake mode. Future work will incorporate additional wake models that may be used in the context of wind farm controls. The Gaussian model provided the best representation of wake characteristics under different atmospheric conditions and different turbine operating conditions. Good agreement was also seen with the Jensen and multi-zone wake models on a smaller subset of data that matched the conditions of the tuning data.
Based on these results, this provides more confidence in wind farm controllers designed using these models. This study provided a first step towards validating these models in the field. In particular, this study focused on the wake of a single turbine. An increased understanding of these models at the wind farm level is needed to determine the potential performance of wind farm control solutions in the field.
The underlying research was collected as part of a project funded by the Department of Energy to investigate wake steering. Please contact the corresponding author for questions regarding the data used in this paper.
Due to the limitations of the field data presented in this paper, FLORIS had to be tuned to capture the near wake behind the turbine. The wake was evaluated primarily at 2.35D (180.95 m) downstream. These parameters were tuned for 5 % turbulence intensity as indicated in the analysis. Below are the FLORIS tuning values for the near-wake lidar comparisons shown in this paper.
-
Jensen wake model
-
ke=0.055
-
kd=0.17
-
For high turbulence cases (>10 % turbulence intensity), ke=0.1.
-
-
Multi-zone wake model
-
ke=0.1
-
kd=0.17
-
-
-
aU=11.7
-
bU=0.72
-
For high turbulence cases (>10 % turbulence intensity), ke=0.13.
-
-
Gaussian wake model
-
ka=0.17
-
kb=0.06
-
The authors declare that they have no conflict of interest.
The Alliance for Sustainable Energy, LLC (Alliance) is the manager and
operator of the National Renewable Energy Laboratory (NREL). NREL is a
national laboratory of the U.S. Department of Energy, Office of Energy
Efficiency and Renewable Energy. This work was authored by the Alliance and
supported by the U.S. Department of Energy under contract no.
DE-AC36-08GO28308. Funding was provided by the U.S. Department of Energy
Office of Energy Efficiency and Renewable Energy, Wind Energy Technologies
Office. The views expressed in the article do not necessarily represent the
views of the U.S. Department of Energy or the U.S. government. The U.S.
government retains, and the publisher, by accepting the article for
publication, acknowledges that the U.S. government retains a nonexclusive,
paid-up, irrevocable, worldwide license to publish or reproduce the published
form of this work, or allow others to do so, for U.S. government
purposes.
Edited by: Raúl Bayoán
Cal
Reviewed by: two anonymous referees
Abkar, M. and Porté-Agel, F.: Influence of atmospheric stability on wind-turbine wakes: A large-eddy simulation study, Phys. Fluids, 27, 035104, https://doi.org/10.1063/1.4913695, 2015. a, b, c, d
Annoni, J., Gebraad, P. M., Scholbrock, A. K., Fleming, P. A., and Wingerden, J.-W. v.: Analysis of axial-induction-based wind plant control using an engineering and a high-order wind plant model, Wind Energy, 19, 1135–1150, https://doi.org/10.1002/we.1891, 2016. a
Bastankhah, M. and Porté-Agel, F.: A new analytical model for wind-turbine wakes, Renew. Energ., 70, 116–123, 2014. a, b
Bastankhah, M. and Porté-Agel, F.: Experimental and theoretical study of wind turbine wakes in yawed conditions, J. Fluid Mech., 806, 506–541, 2016. a, b, c, d, e, f, g
Boersma, S., Doekemeijer, B., Gebraad, P., Fleming, P., Annoni, J., Scholbrock, A., Frederik, J., and van Wingerden, J.: A tutorial on control-oriented modeling and control of wind farms, in: Proceedings of the American Control Conference (ACC), Seattle, USA, 2017. a
Burton, T., Sharpe, D., Jenkins, N., and Bossanyi, E.: Wind energy handbook, John Wiley & Sons, 2001. a, b
Campagnolo, F., Petrović, V., Bottasso, C. L., and Croce, A.: Wind tunnel testing of wake control strategies, in: American Control Conference (ACC), 2016, 513–518, IEEE, 2016. a
Chamorro, L. P. and Porté-Agel, F.: Turbulent flow inside and above a wind farm: a wind-tunnel study, Energies, 4, 1916–1936, 2011. a
Dilip, D. and Porté-Agel, F.: Wind Turbine Wake Mitigation through Blade Pitch Offset, Energies, 10, 757, https://doi.org/10.3390/en10060757, 2017. a, b
Fleming, P. A., Ning, A., Gebraad, P. M., and Dykes, K.: Wind plant system engineering through optimization of layout and yaw control, Wind Energy, 19, 329–344, 2016. a
Fleming, P., Annoni, J., Scholbrock, A., Quon, E., Dana, S., Schreck, S., Raach, S., Haizmann, F., and Schlipf, D.: Full-Scale Field Test of Wake Steering, Wake Conference, Visby, Sweden, 2017a. a, b
Fleming, P., Annoni, J., Shah, J. J., Wang, L., Ananthan, S., Zhang, Z., Hutchings, K., Wang, P., Chen, W., and Chen, L.: Field test of wake steering at an offshore wind farm, Wind Energ. Sci., 2, 229–239, https://doi.org/10.5194/wes-2-229-2017, 2017b. a, b, c
Fleming, P. A., Gebraad, P. M., Lee, S., van Wingerden, J.-W., Johnson, K., Churchfield, M., Michalakes, J., Spalart, P., and Moriarty, P.: Evaluating techniques for redirecting turbine wakes using SOWFA, Renew. Energ., 70, 211–218, 2014. a
Fleming, P., Annoni, J., Churchfield, M., Martinez-Tossas, L. A., Gruchalla, K., Lawson, M., and Moriarty, P.: A simulation study demonstrating the importance of large-scale trailing vortices in wake steering, Wind Energ. Sci., 3, 243–255, https://doi.org/10.5194/wes-3-243-2018, 2018. a, b
Frandsen, S., Barthelmie, R., Pryor, S., Rathmann, O., Larsen, S., Højstrup, J., and Thøgersen, M.: Analytical modelling of wind speed deficit in large offshore wind farms, Wind Energy, 9, 39–53, 2006. a
Gebraad, P., Teeuwisse, F., Wingerden, J., Fleming, P., Ruben, S., Marden, J., and Pao, L.: Wind plant power optimization through yaw control using a parametric model for wake effects—a CFD simulation study, Wind Energy, 19, 95–114, 2016. a, b, c, d, e, f, g, h, i, j, k
Gebraad, P. M. and Van Wingerden, J.: A control-oriented dynamic model for wakes in wind plants, J. Phys. Conf. Ser., 524, p. 012186, IOP Publishing, 2014. a
Howland, M. F., Bossuyt, J., Martínez-Tossas, L. A., Meyers, J., and Meneveau, C.: Wake structure in actuator disk models of wind turbines in yaw under uniform inflow conditions, J. Renew. Sustain. Ener., 8, 043301, https://doi.org/10.1063/1.4955091, 2016. a
Jensen, N. O.: A note on wind generator interaction, Tech. Rep. Risø-M-2411, Risø, 1983. a, b
Jiménez, Á., Crespo, A., and Migoya, E.: Application of a LES technique to characterize the wake deflection of a wind turbine in yaw, Wind Energy, 13, 559–572, 2010. a, b
Johnson, K. E. and Thomas, N.: Wind farm control: Addressing the aerodynamic interaction among wind turbines, American Control Conference, 2104–2109, 2009. a
Johnson, K. E., Pao, L. Y., Balas, M. J., and Fingersh, L. J.: Control of variable-speed wind turbines: standard and adaptive techniques for maximizing energy capture, IEEE Contr. Syst. Mag., 26, 70–81, 2006. a
Jonkman, J.: NWTC Design Codes – FAST, https://nwtc.nrel.gov/FAST (last access: September 2017), 2010. a
Katic, I., Højstrup, J., and Jensen, N. O.: A simple model for cluster efficiency, in: European wind energy association conference and exhibition, 407–410, 1986. a, b
Niayifar, A. and Porté-Agel, F.: A new analytical model for wind farm power prediction, J. Phys. Conf. Ser., 625, p. 012039, IOP Publishing, 2015. a, b, c, d, e, f, g, h
Pope, S. B.: Turbulent flows, Cambridge university press, 2000. a
Raach, S., Schlipf, D., and Cheng, P. W.: Lidar-based wake tracking for closed-loop wind farm control, J. Phys. Conf. Ser., 753, p. 052009, IOP Publishing, 2016. a, b, c, d
Raach, S., Boersma, S., van Wingerden, J.-W., Schlipf, D., and Cheng, P. W.: Robust lidar-based closed-loop wake redirection for wind farm control, IFAC-PapersOnLine, 50, 4498–4503, 2017. a
Schottler, J., Hölling, A., Peinke, J., and Hölling, M.: Wind tunnel tests on controllable model wind turbines in yaw, in: 34th Wind Energy Symposium, vol. 1523, 2016. a
Smalikho, I., Banakh, V., Pichugina, Y., Brewer, W., Banta, R., Lundquist, J., and Kelley, N.: Lidar investigation of atmosphere effect on a wind turbine wake, J. Atmos. Ocean. Tech., 30, 2554–2570, 2013. a
Stanley, A. P., Thomas, J., Ning, A., Annoni, J., Dykes, K., and Fleming, P.: Gradient-Based Optimization of Wind Farms with Different Turbine Heights, in: 35th Wind Energy Symposium, p. 1619, 2017. a
Stull, R. B.: An introduction to boundary layer meteorology, vol. 13, Springer Science & Business Media, 2012. a, b
Thomas, J., Tingey, E., and Ning, A.: Comparison of two wake models for use in gradient-based wind farm layout optimization, in: Technologies for Sustainability (SusTech), 2015 IEEE Conference on, 203–208, IEEE, 2015. a
Vollmer, L., Steinfeld, G., Heinemann, D., and Kühn, M.: Estimating the wake deflection downstream of a wind turbine in different atmospheric stabilities: an LES study, Wind Energ. Sci., 1, 129–141, https://doi.org/10.5194/wes-1-129-2016, 2016. a, b