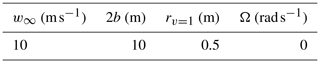A vortex-based tip/smearing correction for the actuator line

The actuator line (AL) was intended as a lifting line (LL) technique for computational fluid dynamics (CFD) applications. In this paper we prove – theoretically and practically – that smearing the forces of the actuator line in the flow domain forms a viscous core in the bound and shed vorticity of the line. By combining a near-wake representation of the trailed vorticity with a viscous vortex core model, the missing induction from the smeared velocity is recovered. This novel dynamic smearing correction is verified for basic wing test cases and rotor simulations of a multimegawatt turbine. The latter cover the entire operational wind speed range as well as yaw, strong turbulence and pitch step cases. The correction is validated with lifting line simulations with and without viscous core, which are representative of an actuator line without and with smearing correction, respectively. The dynamic smearing correction makes the actuator line effectively act as a lifting line, as it was originally intended.

1 Introduction

The actuator line (AL) technique developed by Sørensen and Shen (2002) is a lifting line (LL) representation of the wind turbine rotor suitable for computational fluid dynamics (CFD) simulations. It captures transient physical features like shed and trailed vorticity (including root/tip vortices), without the computational cost associated with resolving the full rotor geometry. Thus, the AL model enables large-eddy simulations (LES) of large wind farms in realistic, turbulent atmospheric boundary layers (Vollmer et al., 2017).

However, in contrast to LL vortex formulations, the blade forces are dispersed in the flow domain – most commonly in form of a Gaussian projection – to avoid numerical instabilities. A length scale – also referred to as smearing coefficient – controls this force redistribution, the lower limit of which is linked to the grid size by numerical stability requirements (Troldborg et al., 2009). Mikkelsen (2003) observed a large sensitivity of the blade velocities to this length scale, which consequently also propagated to the blade forces. Especially in regions along the blade exhibiting stark load changes, such as around the root and tip, forces are substantially over-predicted, meaning that this effect is exacerbated by non-tapered and low-aspect-ratio blades. As actuator disc formulations suffer from similar issues towards the blade tip, Glauert (1935) type tip corrections are also frequently applied to ALs (Shen et al., 2005). However, these correct discs for missing discrete blades and should therefore be unnecessary – strictly even invalid – for ALs. Shives and Crawford (2013) and Jha et al. (2014) achieved a reduction in the force over-prediction by varying the originally fixed smearing factor with respect to the blade chord. However, their methods cannot decouple the blade forces from the smearing length scale: a smeared force distribution in the flow domain unavoidably leads to lower induction at the blade – increasing lift and drag – compared with an actual LL with a concentrated, spatially singular force.

1.1 The vortex smearing hypothesis

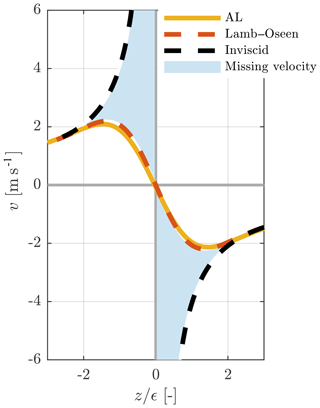
Shives and Crawford (2013) noticed the similarity between the velocities induced across an actuator line and those predicted by a viscous vortex core model. These models include the limiting effect of viscous shear forces on the induced velocities around vortex cores. A similar comparison of the swirl velocities about an infinite vortex line is shown in Fig. 1 – here with a Lamb–Oseen vortex core model (Lamb, 1932; Oseen, 1911). Without viscosity (inviscid) the velocities approach infinity towards the vortex centre. The startling agreement between the Lamb–Oseen and AL velocities was first demonstrated by Dag et al. (2017). The Gaussian body force smearing in the AL technique thus produces similar swirl velocities to a viscous vortex. Ignoring viscous effects, the AL should, in principle, induce the same velocities as a LL – equivalent to the inviscid solution. The missing induced velocity in the AL model (shaded area in Fig. 1) can be approximated following Dag et al. (2017) as follows:

$$\begin{array}{ll}{\displaystyle }\mathrm{\Delta }{v}_{\mathit{\theta }}\left(r\right)& {\displaystyle }=\stackrel{\text{inviscid}}{\overbrace{{\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{2}\mathit{\pi }r}}}}-\stackrel{\text{viscous core}}{\overbrace{{\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{2}\mathit{\pi }r}}\left[\mathrm{1}-\exp \left(-r^{\mathrm{2}}/{\mathit{ϵ}}^{\mathrm{2}}\right)\right]}}\\ \text{(1)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{2}\mathit{\pi }r}}\exp \left(-r^{\mathrm{2}}/{\mathit{ϵ}}^{\mathrm{2}}\right),\end{array}$$

where Γ represents the vortex line's circulation, r is the distance from the vortex core and ϵ is the length scale used in the force smearing. This formulation can be split into an inviscid and viscous/smearing contribution:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Delta }{v}_{\mathit{\theta }}\left(r\right)=\stackrel{\text{inviscid}}{\overbrace{v_{\mathit{\theta }}\left(r\right)}}\underset{\text{smearing}}{\underbrace{f_{\mathit{ϵ}}\left(r_{\mathit{ϵ}}\right)}}\text{with}{v}_{\mathit{\theta }}\left(r\right)={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{2}\mathit{\pi }r}},\\ \text{(2)}& {\displaystyle }& {\displaystyle }{f}_{\mathit{ϵ}}\left(r_{\mathit{ϵ}}\right)=\exp (-r_{\mathit{ϵ}}^{\mathrm{2}}),r_{\mathit{ϵ}}={\displaystyle \frac{r}{\mathit{ϵ}}}.\end{array}$$

If this viscous behaviour of the force smearing in AL simulations was limited to the bound vortex representing the blade, it would not influence the blade forces as long as the blade was straight. However, Dag et al. (2017) argued that the trailing vortices (in the wake) exhibit the same viscous core, as they originate from the bound vortex. Hence, the wake of an AL induces lower velocities at the blade than a LL. The missing velocity can be estimated from the viscous core equivalence and thus correct the velocities at the blade. This mostly impacts blade forces by changing the angle of attack at the blade sections.

Figure 1 Distribution of the tangential velocity component in a plane orthogonal to an infinite vortex line (along x) obtained from either an inviscid or viscous (Lamb–Oseen) theoretical vortex and an actuator line (AL) CFD simulation.

1.2 Contributions of this paper

Dag et al. (2017) corrected AL simulations of a rectangular wing and two rotors with different aspect ratios by recuperating the missing induced velocity introduced by the viscous core. For all of their simulations they were able to show the beneficial effect of the correction on the blade load distribution – represented by more physical behaviour, especially towards the tip and root. However, their implementation of the correction did not fully couple the flow field with the blade forces and the induction correction.

The major contributions of this paper are as follows:

• The development of a tuning-free, dynamic and numerically robust smearing correction, which is fully coupled to the AL model.

• A theoretical proof of the force smearing – vortex core equivalence.

• Proof of the vortex core inheritance in trailed vorticity.

• The confirmation of the missing velocity assumption by comparing LL simulations with/without viscous core and AL results with/without correction.

The test cases include constantly and elliptically loaded wings as well as rotor simulations of a multimegawatt turbine covering the entire operational wind speed range. As the AL model is especially attractive for wind farm simulations, the focus here is on coarsely resolved ALs. The correct dynamic behaviour of the new correction is verified through yawed inflow and pitch step simulations.

2 Proof of force smearing – vortex core equivalence

The equivalence between the velocity field induced by an AL and a viscous vortex can be derived directly from the incompressible Navier–Stokes equations. This proof follows the approach by Forsythe et al. (2015) that successfully connected an AL's vorticity field to its force projection. Starting by taking the curl of the incompressible momentum equation, the vorticity transport equation is obtained ($\mathit{\omega }=\mathrm{\nabla }\times \mathit{u}$):

$$\begin{array}{}\text{(3)}& \underset{\begin{array}{c}=\mathrm{0}\\ \text{steady}\end{array}}{\underbrace{{\displaystyle \frac{\partial \mathit{\omega }}{\partial t}}}}+\left(\mathit{u}\mathrm{\nabla }\right)\mathit{\omega }=\underset{\begin{array}{c}=\mathrm{0}\\ \mathrm{2}D\end{array}}{\underbrace{\left(\mathit{\omega }\mathrm{\nabla }\right)\mathit{u}}}+\underset{\begin{array}{c}=\mathrm{0}\\ \text{inviscid}\end{array}}{\underbrace{\mathit{\nu }{\mathrm{\nabla }}^{\mathrm{2}}\mathit{\omega }}}+\mathrm{\nabla }{\displaystyle \frac{\mathit{f}}{\mathit{\rho }}},\end{array}$$

where ν is the viscosity, ρ is density and f represents the body forces from the AL. Away from the root and tip, the flow around a high-aspect-ratio blade is nearly two-dimensional, as the span-wise flow is negligible. Viscous effects are disregarded in light of the large Reynolds numbers encountered. Furthermore the relationship between the body force and flow field becomes quasi-steady assuming the flow is attached. Cancelling the respective terms and noting that in two-dimensional flow (y−z plane) $\mathit{\omega }={\mathit{\omega }}_x{\widehat{\mathit{e}}}_x$ and $\mathrm{\nabla }=(\mathrm{0},\frac{\partial }{\partial y},\frac{\partial }{\partial z})$:

$$\begin{array}{}\text{(4)}& \left(\mathit{u}\mathrm{\nabla }\right){\mathit{\omega }}_x{\widehat{\mathit{e}}}_x=\mathrm{\nabla }{\displaystyle \frac{\mathit{f}}{\mathit{\rho }}}.\end{array}$$

Assuming the drag to be negligible, the force – in the form of lift – exerted by the AL on the flow in terms of its circulation Γ becomes

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }\mathit{f}=-{\mathit{f}}_{\text{aero}}g\left(r\right)\text{(6)}& {\displaystyle }& {\displaystyle }{\mathit{f}}_{\text{aero}}=L=\mathit{\rho }\mathit{u}\times \mathrm{\Gamma }{\widehat{\mathit{e}}}_{x}g\left(r\right)={\displaystyle \frac{\mathrm{1}}{\mathit{\pi }{\mathit{ϵ}}^{\mathrm{2}}}}\exp (-r^{\mathrm{2}}/{\mathit{ϵ}}^{\mathrm{2}}).\end{array}$$

Here g represents a two-dimensional Gaussian force projection with r indicating the distance from the AL. Inserting these expression into Eq. (4) and exploiting standard matrix transformation and mass conservation¹

$$\begin{array}{}\text{(7)}& {\displaystyle }\left(\mathit{u}\mathrm{\nabla }\right){\mathit{\omega }}_x{\widehat{\mathit{e}}}_x& {\displaystyle }=\mathrm{\nabla }(\mathrm{\Gamma }g{\widehat{\mathit{e}}}_x\times \mathit{u})=\left(\mathit{u}\mathrm{\nabla }\right)\mathrm{\Gamma }g{\widehat{\mathit{e}}}_x\text{(8)}& {\displaystyle }\left(\mathit{u}\mathrm{\nabla }\right){\mathit{\omega }}_x& {\displaystyle }=\left(\mathit{u}\mathrm{\nabla }\right)\mathrm{\Gamma }g.\end{array}$$

Due to mass conservation the u∇ term can be inverted; this gives a direct relationship between the force projection and vorticity:

$$\begin{array}{}\text{(9)}& {\mathit{\omega }}_x=\mathrm{\Gamma }g={\displaystyle \frac{\mathrm{\Gamma }}{\mathit{\pi }{\mathit{ϵ}}^{\mathrm{2}}}}\exp (-r^{\mathrm{2}}/{\mathit{ϵ}}^{\mathrm{2}}).\end{array}$$

As the body force is axially symmetric, the vorticity only induces tangential velocities

$$\begin{array}{ll}{\displaystyle }{\mathit{\omega }}_x\left(r\right)& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{r}}\left({\displaystyle \frac{\partial r{u}_{\mathit{\theta }}}{\partial r}}-\underset{\begin{array}{c}=\mathrm{0}\\ \text{axisymmetry}\end{array}}{\underbrace{{\displaystyle \frac{\partial u_r}{\partial \mathit{\theta }}}}}\right)\\ \text{(10)}& {\displaystyle }& {\displaystyle }\Rightarrow u_{\mathit{\theta }}={\displaystyle \frac{\mathrm{1}}{r}}\underset{\mathrm{0}}{\overset{r}{\int }}r{\mathit{\omega }}_x\left(r\right)\mathrm{d}r.\end{array}$$

Inserting Eq. (9) and integrating gives the swirl velocity induced by a smeared body force

$$\begin{array}{}\text{(11)}& u_{\mathit{\theta }}={\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{2}\mathit{\pi }r}}\left[\mathrm{1}-\exp (-r^{\mathrm{2}}/{\mathit{ϵ}}^{\mathrm{2}})\right].\end{array}$$

This expression equals that of the Lamb–Oseen vortex, only with the viscous core radius replaced by the smearing coefficient². This marks the theoretical confirmation of the observations by Dag et al. (2017), which additionally indicates that a viscous core behaviour with an AL requires inviscid, two-dimensional and locally steady flow conditions.

3 Numerical methodology

3.1 Actuator line simulations

The discretized incompressible Navier–Stokes equations are solved using DTU's CFD code EllipSys3D (Sørensen, 1995; Michelsen, 1994a, b). The flow is iteratively solved at each time instant by the SIMPLE algorithm (Patanker and Spalding, 1972). Depending on the turbulence model either the third-order accurate QUICK (Leonard, 1979) scheme (RANS) or a fourth-order CDS scheme (LES) discretizes the convective terms. As the flow variables are located at the cell centres, a modified Rhie and Chow (Réthoré and Sørensen, 2012) algorithm avoids pressure–velocity decoupling. Further details regarding the numerical techniques are given in Meyer Forsting et al. (2017). For all comparisons with the LL code, the RANS equations are solved using the k−ω shear-stress transport turbulence closure of Menter (1993). Only the turbulent inflow cases in Sect. 5.2.4 are computed using the DES technique of Strelets (2001). The AL model was implemented by Mikkelsen (2003) in EllipSys3D. We employ a version utilizing three-dimensional Gaussian force projection, which follows the original formulation of Sørensen and Shen (2002). As the AL model is especially attractive for wind farm simulations, the focus here is on coarsely resolved ALs, with either 9 or 19 sections (N_s) along the blade. They are uniformly spaced and discretize the blade starting from the root at 1.5 m to the tip at 63 m. The smearing length scale is connected to the number of sections, such that $\mathit{ϵ}=\mathrm{2}R/(N_s+\mathrm{1})-R$ defining the rotor radius – which ensures that the forces in the domain change smoothly between sections (Nathan, 2018). The tower and nacelle are not modelled.

Figure 2 Numerical box domain with a structured mesh and uniform spacing around the rotor at its centre. Only every eighth grid point is shown.

The numerical domain for the rotor simulations is discretized in a verified, standard manner (Meyer Forsting et al., 2017; Troldborg et al., 2009). It consists of a box with 25R side length that contains an inner box with a uniformly spaced refined mesh of 3.2R edge length at its centre surrounding the rotor (see Fig. 2). To capture the velocity gradients around the AL correctly the mesh spacing is $\mathrm{\Delta }x=R/\mathrm{40}$. This is twice the recommended minimum (Troldborg et al., 2009); however, it delivers more accurate angle of attack estimates at the section centres (Shives and Crawford, 2013). In total, 256 cells discretize the flow domain along each dimension, resulting in 16.8×10⁶ degrees of freedom. All variables, except pressure and its correction, which necessitate special treatment (Sørensen, 1995), obey symmetry conditions on the lateral boundaries, whereas at the inflow and outflow faces they follow Dirichlet and Neumann conditions, respectively. The wing test cases follow the same approach only with N_s=32 and an inner box edge length of 3b, where b is the wing's half-span. This results in 80 cells along each dimension and 5.1×10⁵ degrees of freedom. To ensure that the blade tip remains inside a single cell during one time step $\mathrm{\Delta }t<\mathrm{\Delta }x/\left(\mathrm{\Omega }R\right)$ – with mesh spacing Δx and rotational speed Ω. Without rotation, the term ΩR is replaced by the advection speed of the wake. The kinematic viscosity and air density are kept constant at 1.789 $\times {\mathrm{10}}^{-\mathrm{5}}$ kg m⁻¹ s⁻¹ and 1.225 kg m⁻³, respectively. Simulations are stopped when the thrust residual reaches $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$.

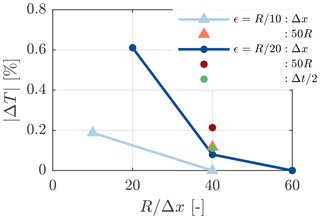
The sensitivity of the rotor thrust to the domain size, time step and grid size is explored in Fig. 3. The length of the domain edges is doubled to 50R, the time step is halved with respect to a set-up obeying the method described above. A simulation of the NREL 5-MW at 8 m s⁻¹ with either 40 or 60 grid cells along the rotor depending on the smearing length scale acts as a reference. With $\mathit{ϵ}=R/\mathrm{10}$ and R∕20, this represents 4 and 3 times the recommended resolution, respectively (Troldborg et al., 2009). Although non-zero, the sensitivity of the results is acceptable in code comparison and should impact AL simulations with and without correction similarly.

Figure 3 Thrust sensitivity of the NREL 5-MW AL simulations at a 8 m s⁻¹ wind speed with respect to grid size, doubling the domain size and halving the time step at two smearing length scales ($N_s=\mathit{\{}\mathrm{9},\mathrm{19}\mathit{\}}$, $T_{\text{ref}}=\mathit{\{}\mathrm{4.20},\mathrm{4.06}\mathit{\}}\times {\mathrm{10}}^{\mathrm{5}}$ N).

3.2 Free-wake lifting line rotor simulations

The in-house solver MIRAS has been employed to perform the free-wake lifting line simulations. MIRAS is a multi-fidelity computational vortex model, which is mainly used for predicting the aerodynamic behaviour of wind turbines and their wakes. It has been developed at DTU over the last decade and been extensively validated for small to large size wind turbine rotors by Ramos-García et al. (2017, 2014a, b).

The free-wake vortex method essentially models the wake of a wind turbine using a bundle of infinitely thin vortex filaments. To avoid numerical singularities, a viscous core must be introduced, which represents a more physical distribution of the velocities induced by each vortex filament, desingularizing the Biot–Savart law near the centre of the filament. The velocity induced by each one of the elements is obtained directly by evaluating the Biot–Savart law, and by summing the velocity induced by all filaments, the total wake induction is obtained as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{u}\left({\mathit{x}}_i\right)=\sum _{j=\mathrm{1}}^N{K}_{ij}{\displaystyle \frac{{\mathit{\gamma }}_j}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{{\mathit{t}}_j\times {\mathit{r}}_{ij}}{r_{ij}^{\mathrm{3}}}},\\ \text{(12)}& {\displaystyle }& {\displaystyle }\text{where}{K}_{ij}={\displaystyle \frac{r_{ij}^{\mathrm{2}}}{{\left({\mathit{\epsilon }}_j^{\mathrm{2}z}+r_{ij}^{\mathrm{2}z}\right)}^{\mathrm{1}/z}}},\end{array}$$

N is total number of filaments that form the wake, ${\mathit{r}}_{ij}={\mathit{x}}_i-{\mathit{y}}_j$ is the distance vector from the vortex element y_j to the evaluation point x_i, γ_j is the circulation of the filament, t_j is the unit orientation vector of the jth filament and $r_{ij}=\left|{\mathit{r}}_{ij}\right|$, ε_j is the vortex core radius of the filament, and z defines the cut-off velocity profile where the Lamb–Oseen model (Lamb, 1932; Oseen, 1911), z=2, has been employed.

A viscous core model is applied to emulate the effect of viscosity by changing the vortex core radius as a function of time (Leishman et al., 2002):

$$\begin{array}{}\text{(13)}& {\mathit{\epsilon }}_i\left(t\right)=\sqrt{\mathrm{4}{\mathit{\alpha }}_v{\mathit{\delta }}_v\mathit{\nu }{t}_i}+{\mathit{\epsilon }}_{\mathrm{0}},\end{array}$$

where α_v is a constant set to 1.25643 (Ananthan and Leishman, 2004), ν is the kinematic viscosity and t_i is the time elapsed since the generation of the ith filament. In order to represent the diffusive timescales, the viscous core radius is set to change with the vortex age by adding a turbulence eddy viscosity, δ_v, first proposed by Squire (1965), and in this work set to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$. To avoid the singular behaviour of newly released vortex elements, an initial core radius, ε₀, is introduced. In accordance with Ramos-García et al. (2017), who found that a small core radius is necessary to have flow convergence, a core radius of 0.1 % of the local chord at the release station is used.

For the sake of the present study, two different approaches to compute the angle of attack have been followed.

• Inviscid (LL), where the non-regularized Biot–Savart law is used to compute the induction from the wake filaments at the quarter-chord location. This is the standard method used in a lifting line solvers.

• Viscous (LL+core), where the regularized Biot–Savart law is used to compute the induction at the quarter-chord location. A viscous core with a radius equal to the actuator line smearing factor is used for a direct comparison of the methods.

This enables a double validation of the models. On the one hand the corrected AL simulations can be validated against the LL calculations, and on the other hand the raw AL model, without tip correction, can be compared against the LL+core simulations which include the smearing effect in the free-wake model.

4 Tip/smearing correction for the actuator line

Applying the velocity correction methodology introduced in Sect. 1.1 in three-dimensional space yields a velocity correction vector. The viscous core behaviour of the AL bound vorticity – proven in Sect. 2 to originate from the force smearing – is inherited by the trailing vortices, as will be demonstrated in Sect. 5.1.1. Therefore, the induction from the trailed vorticity at the blade is lower than without force smearing. Figure 4 shows the path of trailed vorticity shed from in-between two sections of a blade with a strength of $\mathrm{\Delta }\mathrm{\Gamma }={\mathrm{\Gamma }}_s-{\mathrm{\Gamma }}_{s+\mathrm{1}}$ with

$$\begin{array}{}\text{(14)}& {\mathrm{\Gamma }}_s={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sqrt{v_s^{\mathrm{2}}+w_s^{\mathrm{2}}}{C}_{\mathrm{L}}\left(\mathit{\alpha }\right)c.\end{array}$$

Here s defines the blade section index, C_L is the sectional lift coefficient, c is the section chord and α is the angle of attack, which depends on the inflow angle in combination with blade pitch and twist at the section. The missing induction from this single trailed vortex at a point C is obtained by integrating along the vortex line

$$\begin{array}{}\text{(15)}& {\mathit{u}}^{*}=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{f}_{\mathit{ϵ}}\mathit{\delta }\stackrel{\mathrm{̃}}{\mathit{u}}\text{d}l,\end{array}$$

where l is the vortex following coordinate. Here $\mathit{\delta }\stackrel{\mathrm{̃}}{\mathit{u}}$ is the velocity induced by an infinitesimal element δl of the vortex line at point C, which is given by the Biot–Savart law:

$$\begin{array}{}\text{(16)}& \mathit{\delta }\stackrel{\mathrm{̃}}{\mathit{u}}={\displaystyle \frac{\mathrm{\Delta }\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{\mathit{\delta }\mathit{l}\times \mathit{x}}{|\mathit{x}{|}^{\mathrm{3}}}},\end{array}$$

where x is the vector pointing from the element towards C. The smearing factor for this vortex element becomes

$$\begin{array}{}\text{(17)}& f_{\mathit{ϵ}}=\exp \left(-{\displaystyle \frac{(\mathit{x}{\widehat{\mathit{e}}}_{⟂}{)}^{\mathrm{2}}}{{\mathit{ϵ}}^{\mathrm{2}}}}\right).\end{array}$$

The viscous core only acts in the plane orthogonal to the vortex element δl; hence, ${\widehat{\mathit{e}}}_{⟂}$ projects x onto this plane. This is different to using the distance, $\left|\mathit{x}\right|$, as Dag et al. (2017) proposed, which violates the two-dimensional nature of the viscous core.

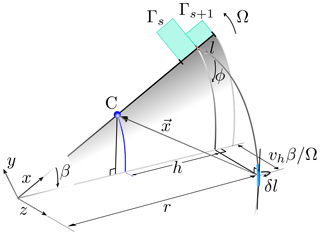
Figure 4 Trailed vorticity path. The blade rotates in the x−y plane and z points downstream. The vortex element δl with a strength of ${\mathrm{\Gamma }}_s-{\mathrm{\Gamma }}_{s+\mathrm{1}}$ is shed at r and transported downstream by the local velocity. The distance from the shedding location r to a point C along the blade is h ($h=r-C_x$), where δl induces tangential and axial velocities.

The total missing induction at a blade section s is obtained by summing the contribution from all trailed vortices. The number of trailed vortices N_v is directly related to the number of blade sections $N_v=N_s+\mathrm{1}$. Discretizing the vortices in time, the missing induction at a certain blade section becomes

$$\begin{array}{}\text{(18)}& {\mathit{u}}_s^{*}=\sum _v^{N_v}\sum _n^{N_t}{f}_{s,v}^n\mathbf{\Delta }{\stackrel{\mathrm{̃}}{\mathit{u}}}_{s,v}^n.\end{array}$$

Here v denotes the trailed vortex index, n is the time index and N_t is the number of time steps. Note that n=1 is the most recently shed vortex element. As a tip/smearing correction should remain computationally inexpensive, numerically solving the Biot–Savart law in Eq. (16) to obtain $\mathbf{\Delta }{\stackrel{\mathrm{̃}}{\mathit{u}}}_{s,v}^n$ is unfeasible. This would necessitate N_tN_vN_s or N_t(N_s+1)N_s evaluations. An accurate, yet fast, alternative to solving the Biot–Savart law directly is the near-wake model (NWM) for trailed vorticity by Pirrung et al. (2016, 2017b), which also includes downwind convection. It performs well for dynamic flow cases and exhibits great numerical stability, as it was originally developed to enhance the aerodynamic accuracy of blade element momentum (BEM) models. Its formulation is based on a lifting line representation of the blade's trailed vorticity as depicted in Fig. 4 and approximates the induced velocities from a single trailed vortex line by two indicial functions. The velocity induced by a vortex element is given in the NWM as

$$\begin{array}{}\text{(19)}& \mathbf{\Delta }{\stackrel{\mathrm{̃}}{\mathit{u}}}_{s,v}^n=\left(X_{s,v}^n+Y_{s,v}^n\right)\left[\begin{array}{c}\mathrm{0}\\ \sin \left({\mathit{\varphi }}^n\right)\\ -\cos \left({\mathit{\varphi }}^n\right)\end{array}\right],\end{array}$$

with ϕ representing the helix angle of the vorticity shed in the CFD domain (see Fig. 4). The indicial functions take the following form:

$$\begin{array}{ll}{\displaystyle }\left\{X_{s,v}^n,Y_{s,v}^n\right\}& {\displaystyle }=a_{\left\{X,Y\right\}}{\displaystyle \frac{r_v}{\mathrm{4}\mathit{\pi }{h}_s\left|h_s\right|}}\mathrm{\Delta }{\mathrm{\Gamma }}_v^n{\mathit{\varphi }}_{s,v}^{{*}^n}\\ {\displaystyle }& {\displaystyle }\left[\mathrm{1}-\exp \left(-b_{\left\{X,Y\right\}}{\displaystyle \frac{\mathrm{\Delta }{\mathit{\beta }}^{{*}^n}}{{\mathit{\varphi }}_{s,v}^{{*}^n}}}\right)\right]\\ \text{(20)}& {\displaystyle }& {\displaystyle }\exp \left(-b_{\left\{X,Y\right\}}\sum _i^{n-\mathrm{1}}{\displaystyle \frac{\mathrm{\Delta }{\mathit{\beta }}^{{*}^i}}{{\mathit{\varphi }}_{s,v}^{{*}^i}}}\right).\end{array}$$

The definitions of $a_{\left\{X,Y\right\}},b_{\left\{X,Y\right\}},{\mathit{\beta }}^{*}$ and ϕ^* are those of Pirrung et al. (2016, 2017b). The indicial functions allow for the solution to be time-advanced by a mere multiplication, considerably reducing the model evaluations to N_vN_s+N_v. In the original formulation this removes the need for bookkeeping; however, as the smearing factor also changes with the position of the vortex element, all previously shed elements are advanced individually in this specific implementation. This is only an experimental feature for testing the smearing correction and should be simple to remove in a future, more practical implementation.

Following the lifting line formulation of the NWM shown in Fig. 4 (refer to Appendix A for a detailed mathematical description) the perpendicular distance from the vortex element to C becomes

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{x}}_{⟂}={\displaystyle \frac{\mathit{\delta }\mathit{l}}{\left|\mathit{\delta }\mathit{l}\right|}}\times \mathit{x}=\\ \text{(21)}& {\displaystyle }& {\displaystyle }r\cos \mathit{\varphi }\left(\begin{array}{c}\tan \mathit{\varphi }\left(\mathit{\beta }\cos \mathit{\beta }-\sin \mathit{\beta }\right)\\ -\tan \mathit{\varphi }\left(-\mathrm{1}+h/r+\cos \mathit{\beta }+\mathit{\beta }\sin \mathit{\beta }\right)\\ -\mathrm{1}+\left(\mathrm{1}-h/r\right)\cos \mathit{\beta }\end{array}\right).\end{array}$$

Thus, the smearing factor becomes

$$\begin{array}{}\text{(22)}& f_{s,v}^n=\exp \left(-{\displaystyle \frac{\left|{\mathit{x}}_{\mathbf{⟂}}\right(r_v,{\mathit{\beta }}^n,h_s,{\mathit{\varphi }}^n){|}^{\mathrm{2}}}{{\mathit{ϵ}}^{\mathrm{2}}}}\right).\end{array}$$

When discretizing in time, βⁿ is taken to be at the mid-point of the vortex element.

Finally the missing velocities computed in Eq. (18) correct the original velocities from the CFD simulations

$$\begin{array}{}\text{(23)}& {\mathit{u}}_s={\mathit{u}}_s^{\text{CFD}}+{\mathit{u}}_s^{*}.\end{array}$$

Therefore, the correction influences the blade forces through the angle of attack and the velocity magnitude, although it is the former that dominates. It also changes the circulation at each blade section through Eq. (14) and, thus, the shed vorticity and its induction. Hence determining the correction velocity is an iterative procedure. The correction algorithm is executed after the flow field is solved and takes the following form:

1. Interpolate the velocity vector u^CFD at the section centres from the CFD flow field.

2. Compute the helix angles ϕ, where ${\mathit{\varphi }}_v=-{\tan }^{-\mathrm{1}}\left(\frac{w_{v-\mathrm{1}}^{\text{CFD}}+w_v^{\text{CFD}}}{v_{v-\mathrm{1}}^{\text{CFD}}+v_v^{\text{CFD}}}\right)$ and ${\mathit{\varphi }}_{\left\{\mathrm{1},N_v\right\}}=-{\tan }^{-\mathrm{1}}\left(\frac{w_{\left\{\mathrm{1},N_s\right\}}^{\text{CFD}}}{v_{\left\{\mathrm{1},N_s\right\}}^{\text{CFD}}}\right)$.

3. Combine the CFD velocities with the respective correction from the previous time step n−1, such that ${\mathit{u}}_n={\mathit{u}}_n^{\text{CFD}}+{\mathit{u}}_{n-\mathrm{1}}^{*}$.

4. Compute the smearing factor f_ϵ for all time steps, sections and elements (Eq. 22).

5. Determine the angle of attack and velocity magnitude from u_n to determine Γ_s (Eq. 14)³,

6. Compute the velocities from the newly released vortex element $\mathbf{\Delta }{\stackrel{\mathrm{̃}}{\mathit{u}}}_n$ (Eq. 19).

7. At the first iteration of each time step, advance the previous elements in time.

8. Compute the velocity correction at the current time step ${\mathit{u}}_n^{*}$ (Eq. 18).

9. Update the velocity at the sections with some form of relaxation ${\mathit{u}}_n={\mathit{u}}_n^{\text{CFD}}+{\mathit{u}}_n^{*}$.

10. Repeat steps 5–9 until convergence is reached.

We use the technique by Pirrung et al. (2017a) established for the NWM to accelerate and ensure its convergence. Furthermore, the activation of the correction is delayed until the starting vorticity of the rotor has been transported at least one blade length away from the rotor plane. This enhances its numerical stability, as induction has already built up at the blades by its time of activation.

5 Results

5.1 Basic wing test cases

To verify the smearing hypothesis (Sect. 1.1) and the novel smearing correction (Sect. 4) two basic wing flow cases with known theoretical solutions are modelled using CFD. Either a rectangular or an elliptic wing is represented by an AL as shown in Fig. 5, where the coordinate system is unchanged from the definition in Fig. 4. The AL is discretized in uniformly spaced sections in-line with the underlying flow grid, and the smearing parameter is twice the section width, which ensures a continuous force distribution along the wing. The common simulation parameters are given in Table 1. Unless specifically stated the sectional lift coefficient C_L=1 and drag is zero along the wing, independent of the angle of attack. The chord of the rectangular wing is set to 1 m and the elliptical chord distribution is

$$\begin{array}{}\text{(24)}& c\left(x\right)=c_{\mathrm{0}}\sqrt{\mathrm{1}-{\left({\displaystyle \frac{x-(b+r_{v=\mathrm{1}})}{b}}\right)}^{\mathrm{2}}},\end{array}$$

with the root chord c₀=4 m. All simulations are performed within the same computational domain, defined in Sect. 3.1.

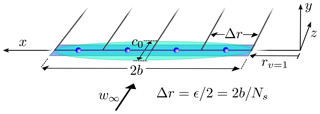
Figure 5 Definition of the wing test cases with either a rectangular or elliptic planform. Vortices are trailed in-between sections and the actuator line forces are computed and exerted at the sections' centres.

Table 1 Input parameters common to both rectangular and elliptic wing simulations.

The theoretical predictions of the velocity field are achieved by representing the vortex system of Fig. 5 with vortex filaments. The velocity induced by a filament with a viscous vortex core at an arbitrary point C is

$$\begin{array}{}\text{(25)}& {\displaystyle }\mathit{u}& {\displaystyle }=f_{\mathit{ϵ}}\left(x_{⟂}\right){\displaystyle \frac{\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{(x_{\mathrm{1}}+x_{\mathrm{2}})({\mathit{x}}_{\mathbf{1}}\times {\mathit{x}}_{\mathbf{2}})}{x_{\mathrm{1}}{x}_{\mathrm{2}}+{\mathit{x}}_{\mathbf{1}}\cdot {\mathit{x}}_{\mathbf{2}}}}\text{(26)}& {\displaystyle }{x}_{⟂}& {\displaystyle }={\displaystyle \frac{|{\mathit{x}}_{\mathbf{1}}\times {\mathit{x}}_{\mathbf{2}}|}{|x_{\mathrm{2}}-x_{\mathrm{1}}|}}\text{and}{x}_i=\left|{\mathit{x}}_i\right|,\end{array}$$

where x₁ points from the start of the filament to C and x₂ from its end. For a definition of f_ϵ(x_⟂) refer to Eq. (17); without viscous core $f_{\mathit{ϵ}}\left(x_{⟂}\right)=\mathrm{1}$. The contribution from different segments is summed to give the overall velocity field. As the wing is lightly loaded, we assume that all vortex segments remain in the x−z plane.

5.1.1 Trailed vorticity smearing

The vortex smearing hypothesis assumes the trailed vorticity inheriting the smeared velocity field from the bound vortex, which was confirmed theoretically by Martínez-Tossas and Meneveau (2019) for straight wings. We test this further by simulating a rectangular wing without any correction. All vorticity is shed from the wing tips, creating the well-known horseshoe vortex. Hence, for the hypothesis to be valid, the velocity distribution in the plane orthogonal to the trailed vortices should be identical to that of the bound vortex .

Figure 6 compares the velocities induced by a rectangular wing predicted by an AL and three vortex segments (one bound, two trailed) for five different smearing parameters. Only half of the wing is presented, due to symmetry. Velocity distributions are shown for lines cutting the vortex segments at right angles for y=0. Clearly the velocity smearing is identical between trailed and bound vorticity, confirming the smearing hypothesis. Slight differences are linked to the numerical discretization of the Gaussian force projection (Shives and Crawford, 2013) and numerical diffusion.

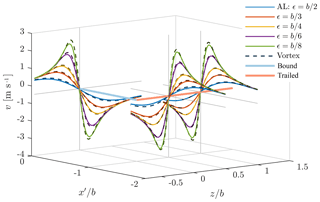
Figure 6 Velocities induced perpendicular to a rectangular wing predicted by an actuator line (AL) without correction and by vortex segments with a viscous core (Vortex) with different smearing parameters. Velocities are shown along lines cutting the bound and trailed vortices at right angles and y=0. Only half of the horseshoe vortex is depicted as $x^{\prime }=x-(b+r_{v=\mathrm{1}})$.

5.1.2 Smearing correction verification

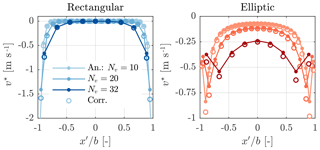
As mentioned in Sect. 4, the new smearing correction uses a lifting line representation of the trailed vorticity. Thus, the prediction of the velocity correction with our model or vortex segments should be identical. To simultaneously verify its numerical implementation, our model only receives the sampled velocities from the flow domain to compute the circulation at the sections. Furthermore, the body forces are not applied inside the domain to avoid influencing the trailed vortex paths, and the correction velocities are not added to the CFD velocities to keep the circulation unchanged. This holds the trailed vortices in the x−z plane, simplifying the representation of the wake with vortex segments. The segments' circulation is exactly the same as in the smearing correction to avoid any numerical effects influencing the comparison. Figure 7 compares the velocity correction predicted by the analytical vortex segments and our model at each section along a rectangular and elliptic wing for different smearing factors (i.e. $\mathit{ϵ}=\mathrm{2}b/(N_v-\mathrm{1})$). With decreasing force smearing the velocity correction concentrates towards the tips, as the induced velocity gradients increase. Therefore, even at higher resolution the smearing correction remains significant, although more localized. Generally the model slightly over-predicts the missing induction at the wing, becoming more prominent with increasing resolution. At N_v=64 the difference reaches a maximum of 6.7 % (rectangular) and 1.7 % (elliptic) with respect to the inflow velocity. The average error does not breach 0.5 % in any case. The velocity jump towards the tip sections of the elliptical wing is related to the equidistant discretization of the wing (Pirrung et al., 2014).

Figure 7 Analytical (An.) and corresponding model prediction of the velocity correction for varying force smearing ($\mathit{ϵ}=\mathrm{2}b/(N_v-\mathrm{1})$) along a rectangular and elliptic wing, where $x^{\prime }=x-(b+r_{v=\mathrm{1}})$.

5.1.3 Coupled AL-smearing correction verification

The coupling between velocity correction and the flow domain is verified by comparing the corrected downwash at an elliptical wing to the theoretical expectation. The downwash should be constant along the wing and is given by

$$\begin{array}{}\text{(27)}& v_{\text{th}}=-{\displaystyle \frac{{\mathrm{\Gamma }}_{\mathrm{0}}}{\mathrm{4}b}}=-{\displaystyle \frac{w_{\mathrm{\infty }}{c}_{\mathrm{0}}{C}_{\mathrm{L}}}{\mathrm{8}b}},\end{array}$$

where Γ₀ is the circulation at the wing root. Similar to Shives and Crawford (2013) the C_L was not fixed, but instead followed the theoretical lift curve slope for thin airfoils C_L=2π. For the wing to operate at a constant lift coefficient C_L=1, its angle of attack needed to include the effect of the induced velocities:

$$\begin{array}{}\text{(28)}& \mathit{\alpha }={\mathit{\alpha }}_{\text{eff}}+{\mathit{\alpha }}_i={\displaystyle \frac{C_{\mathrm{L}}}{\mathrm{2}\mathit{\pi }}}+{\tan }^{-\mathrm{1}}\left({\displaystyle \frac{c_{\mathrm{0}}{C}_{\mathrm{L}}}{\mathrm{8}b}}\right).\end{array}$$

This represents a more rigorous test of the coupled system than prescribing the loading along the wing, as only the correct downwash leads to the desired, constant sectional lift coefficients.

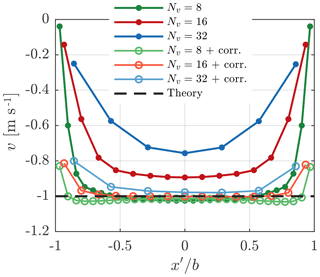
Figure 8 shows the downwash predicted by AL simulations with different smearing parameters and active correction. The CFD components of the velocities are shown (v^CFD) separately to emphasize the contribution of the correction to arrive at the correct, constant downwash of 1 m s⁻¹. Clearly without the correction, the induced velocities are a function of the smearing factor and only arrive at the theoretically expected value for N_v=32. Including the correction greatly reduces the dependence of the downwash on the force smearing. The insufficient correction towards the tips feeds back to the equidistant discretization of the AL (Pirrung et al., 2014), which is linked to the uniform spacing of the underlying flow grid.

Figure 8 Downwash at an elliptical wing predicted by AL simulations with different smearing factors and smearing correction. The CFD components of the velocities are shown (dashed) as well as the total downwash incorporating the correction (solid). The theoretical value acts as reference.

5.2 Rotor simulations – NREL 5-MW

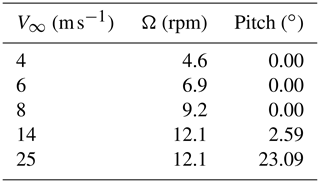
The validity of the smearing hypothesis and its correction in rotor applications is demonstrated with simulations of the NREL 5-MW turbine (Jonkman et al., 2009) using actuator line (AL) and lifting line (LL) models. The input parameters for these simulations are given in Table 2.

Table 2 Input parameters for the NREL 5-MW simulations.

5.2.1 Uniform inflow

Figure 9 compares the AL results with and without the novel smearing correction to the LL with and without viscous core. At this wind speed of 8 m s⁻¹ the thrust coefficient is highest (C_T=0.84) – and hence induction is highest – thus lending itself as a strong verification case. Clearly, there is an equivalence between the original AL and the LL with a viscous core and the corrected AL with the LL. Therefore, the smearing correction makes the AL effectively act as a LL, as originally intended by Sørensen and Shen (2002). The impact of the viscous core is most prominent toward the blade root and tip. The sudden drop in the forces predicted by the AL/LL+core for the tip section of the blade – located at $r/R=\mathrm{0.97}$ – is not triggered by any aerodynamic tip effects, but relates to a pronounced reduction in chord. Figure 10 shows the diminishing effect of the correction on the angle of attack towards the root and tip. As the correction velocities are negligible with respect to the rotational velocity – they impact the velocity magnitude by less than 0.1 % in the lifting region of the blade – it is ultimately the change in the angle of attack that explains the observations in the force distributions. While not greatly affecting the magnitude of the forces in the mid-section of the blade, the viscous core does introduce greater fluctuations in the force distribution. Hence, the missing induction introduced by the viscous core reduces the coupling between neighbouring blade sections. The smearing correction also recovers this behaviour of the LL. Surpassing rated wind speed, forces increase inboard until cut-out. Thus, just before cut-out at 25 ms⁻¹ loading reaches a maximum towards the root, causing an equally pronounced influence of the smearing correction in this region, as demonstrated in Fig. 11. Again, the equivalence of the AL and LL implementations is remarkable. This high wind speed case also demonstrates our correction is not only a tip correction.

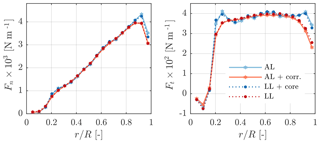
Figure 9 Normal and tangential forces on the NREL 5-MW blades at 8 m s⁻¹ predicted by AL simulations with/without smearing correction and LL with/without viscous core (N_s=19, ϵ=0.1R).

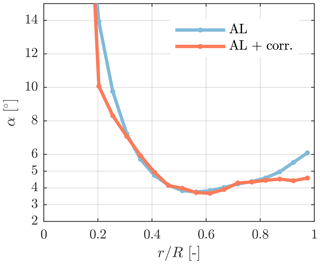
Figure 10 Angle of attack with/without smearing correction on the NREL 5-MW blades at 8 m s⁻¹ (N_s=19, ϵ=0.1R).

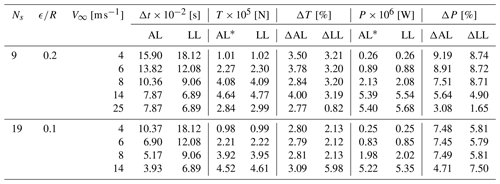
The comparison of AL and LL is summarized in Fig. 12 in the form of local thrust and power distributions at different wind speeds. Note that for the wind speeds below rated (<11.4 m s⁻¹), the coefficients are identical. The results are only presented for simulations with N_s=9 for visibility, but compare equally well at higher resolution. As mentioned earlier, the smearing correction predominantly acts towards the tip and root. An additional overview of all results is given in Table 3. Here the total rotor thrust T and power P predicted by the corrected actuator line (AL^*) and the lifting line (LL) are listed as well as the influence of adding the viscous core relative to AL^* and LL, respectively. The AL and LL solutions are not directly compared to avoid including any mean bias in the comparison. The impact of the correction on the AL forces is nearly identical to removing the viscous core in the LL simulations at any wind speed, which further supports our correction methodology. In light of the large errors incurred without any correction, unsurprisingly, some form of tip correction is usually applied in AL simulations.

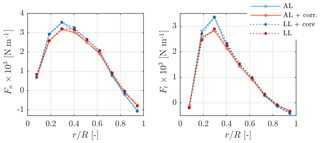
Figure 11 Normal and tangential forces on the NREL 5-MW blades at 25 m s⁻¹ predicted by AL simulations with/without smearing correction and LL with/without viscous core (N_s=9, ϵ=0.2R).

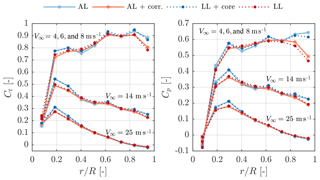
Figure 12 Local thrust and power coefficients along the NREL 5-MW blades at different wind speeds predicted by AL simulations with/without smearing correction and LL with/without core (N_s=9, ϵ=0.2R).

Table 3 An overview of the simulation inputs and results for the NREL 5-MW in uniform inflow. Results are grouped by blade/grid resolution. For the actuator line (AL) and lifting line (LL) the simulation time step Δt, the total thrust T and power P as well as the relative change in these quantities caused by the correction/removing the viscous core are listed. Note that AL^* represents the corrected AL results, and the change is expressed relative to the rotor thrust and power.

5.2.2 Yawed inflow

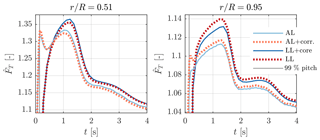
As the smearing correction does not include yaw effects – the wake is assumed to advect normal to the rotor plane – we tested its influence at yaw angles χ of 15,30 and 45^∘ at 8 m s⁻¹. Again the LL with and without viscous core acted as a reference. The time steps remained the same as in uniform inflow. Here only the results for the most extreme case at 45^∘ yaw are shown, as the differences are most severe in this case. Figure 13 presents the normal and tangential force variation during one rotation, averaged over three distinct regions of the blade, at a wind speed of 8 m s⁻¹. Whilst the agreement is best towards the blade tip, the force variation with azimuthal position is similar between AL and LL simulations across all sections. AL results are shifted downwards with respect to the LL predictions at the inner sections, hinting at the AL experiencing higher induction in this region. However, for the verification of the smearing correction this shift is irrelevant, instead its impact on the AL forces needs to be assessed relative to the difference between LL with and without core. In this respect the smearing correction behaves correctly, increasing forces in a similar fashion as a LL without core in the mid-section of the blade and reducing them towards the root and tip.

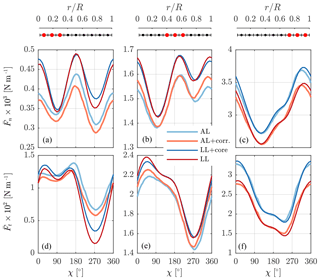
Figure 13 Normal (a, b, c) and tangential (d, e, f) force variation during one rotation as a function of azimuthal position of the NREL 5-MW blades at 8 m s⁻¹ and 45^∘ yaw. The forces are averaged over three sections (inner: a, d; middle: b, e; outer: c, f) of the blade and are predicted by AL simulations with/without smearing correction and LL with/without viscous core. The blade is facing upwind at χ=0^∘ and is pointing vertically up at χ=90^∘ (N_s=9, ϵ=0.2R).

5.2.3 Pitch step

The pitch step is defined as

$$\begin{array}{}\text{(29)}& \mathit{\psi }={\mathit{\psi }}_{\mathrm{0}}+{\displaystyle \frac{\mathrm{\Delta }\mathit{\psi }}{\mathrm{2}}}\left[\mathrm{1}+\tanh \left(k\right(t-t_{\mathrm{0}}\left)\right)\right],\end{array}$$

with ψ₀ defining the pitch angle before the step, t₀ representing the time instant of the step and Δψ denoting the pitch change. Here an extremely violent step is chosen – determined by k – to encourage an equally pronounced blade force response and test the numerical stability of our correction. The parameters governing this comparison are given in Table 4, which realize a pitch step of ±2^∘ in 0.14 s (10 % to 90 % pitch). To capture the swift change in pitch, the time step is adjusted in both AL and LL simulations to $\mathrm{3.94}\times {\mathrm{10}}^{-\mathrm{2}}$ s. The blade force response is normalized as

$$\begin{array}{}\text{(30)}& \widehat{F}\left(t\right)={\displaystyle \frac{F\left(t\right)-F_{\mathrm{0}}}{F_{\mathrm{\infty }}-F_{\mathrm{0}}}},\end{array}$$

with F₀ and F_∞ denoting the steady-state values before and after the pitch step, respectively.

Here only the tangential force response after a +2^∘ step for the mid and tip blade sections are shown in Fig. 14, as they capture the main features of the response. As the definition here is positive pitch to feather, the force decreases along the blade for positive pitch changes. The AL simulations exhibit a faster response with a kink at 0.14 s, coinciding with the pitch change reaching 99 % of the step. Therefore, the AL seems to capture the pitch rate lift. The LL does not show this feature so – as in yaw – the correct behaviour of the smearing correction on the AL force response should be assessed relative to the influence of removing the viscous core in the LL model. Overall, the correction has limited effect on the dynamic response, which is also confirmed by the LL simulations, but the correction essentially acts on the forces in the same fashion as removing the core in the LL. In the mid-section it reduces the forces by a maximum of 1 % during the first 2 s, dropping to 0.5 % afterwards. At the tip section it intensifies the response by a maximum of 1 %, diminishing to 0.3 % at 4 s.

Table 4 Inputs defining the pitch step.

Figure 14 Normalized tangential force response at two blade sections (middle and tip) of the NREL 5-MW following a pitch step of +2^∘ in 0.14 s at 14 m s⁻¹ predicted by AL simulations with/without smearing correction and LL with/without viscous core (N_s=9, ϵ=0.2R).

5.2.4 Turbulent inflow

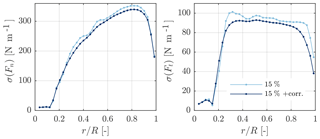
Highly turbulent inflow should challenge the numerical stability of the new smearing correction by introducing strong and abrupt changes in the angle of attack. Comparing simulations with and without inflow turbulence should also reveal whether turbulence alters the nature of the correction. Figure 15 shows the impact of the smearing correction on the time-averaged normal and tangential blade forces at an 8 m s⁻¹ mean wind speed for AL simulations with uniform and turbulent inflow. At a turbulence intensity (TI) of 15 %, the forces are unsurprisingly slightly larger (≈20 N m⁻¹) than in uniform inflow. However, the change in forces introduced by the correction is nearly identical (<2 N m⁻¹). When comparing the standard deviation of the forces with and without correction in Fig. 16 the smoothing and dampening effect of the smearing correction on the forces in highly turbulent inflow also becomes apparent. Madsen et al. (2018) observed a corresponding reduction of the force variations on the whole rotor blade when comparing near-wake model results against BEM results for the NM 80 rotor in turbulent inflow. This illustrates that the smearing correction leads to the same dynamic coupling between neighbouring blade sections as a lifting line model.

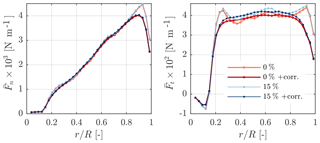
Figure 15 Time-averaged normal and tangential forces on the NREL 5-MW blades at an 8 m s⁻¹ mean wind speed and changing inflow turbulence predicted by the AL model with and without smearing correction (N_s=35, $\mathit{ϵ}=R/\mathrm{8}$).

Figure 16 Variation of normal and tangential forces on the NREL 5-MW blades at an 8 m s⁻¹ mean wind speed and turbulence intensity of 15 % predicted by the AL model with and without smearing correction (N_s=35, $\mathit{ϵ}=R/\mathrm{8}$).

6 Conclusions

The actuator line was intended as a lifting line technique for CFD applications. In this paper we prove – theoretically and practically – that smearing the forces of the actuator line in the flow domain leads to smeared velocity fields. For the typical Gaussian force projection, the widely known Lamb–Oseen (Lamb, 1932; Oseen, 1911) viscous core appears in both bound and trailed vorticity. This core reduces the velocities approaching the vortex centre compared with the inviscid solution of the lifting line. Thus, the trailed vorticity of an actuator line induces lower velocities at the blade owing to the force projection. We recover this missing induction by combining a near-wake model of the trailed vorticity with the Lamb–Oseen viscous core model and coupling it with the actuator line model. Basic wing test cases with theoretical solutions verify the correction, as it recovers nearly all induction independent of the severity of the force smearing. Furthermore, rotor simulations show the applicability and strength of the correction over the entire operational wind speed range as well as in yaw, strong turbulence and undergoing pitch steps. Here the correction is validated with lifting line simulations with and without viscous core, which are representative of an actuator line with and without smearing correction, respectively. The agreement between the respective actuator line and lifting line results is remarkable.

The current implementation of the smearing correction relies on heavy bookkeeping. In future versions the latter will be removed without jeopardizing stability or accuracy, making it suitable for wind farm simulations in realistic atmospheric flows. Potentially, the correction might also enable accurate rotor simulations at lower discretization.

Appendix A: Fixed-wake equations

The equations governing the fixed-wake approach underlying the smearing correction (see Fig. 4) are summarized for completeness.

Direction vector from the vortex element to a control point along the blade:

$$\begin{array}{}\text{(A1)}& \mathit{x}=\left(\begin{array}{c}-r\cos \mathit{\beta }+r-h\\ r\sin \mathit{\beta }\\ -v_h\mathit{\beta }/\mathrm{\Omega }\end{array}\right).\end{array}$$

Definition of the vortex element:

$$\begin{array}{}\text{(A2)}& \mathit{\delta }\mathit{l}=\mathit{\delta }l\cos \mathit{\varphi }\left(\begin{array}{c}-\sin \mathit{\beta }\\ -\cos \mathit{\beta }\\ v_h/\left(\mathrm{\Omega }r\right)\end{array}\right)\end{array}$$

with $\mathit{\delta }l=\frac{r\mathit{\delta }\mathit{\beta }}{\cos \mathit{\varphi }}$. Note that

$$\begin{array}{}\text{(A3)}& \cos \mathit{\varphi }={\displaystyle \frac{\mathrm{\Omega }r}{\sqrt{{\left(\mathrm{\Omega }r\right)}^{\mathrm{2}}+v_h^{\mathrm{2}}}}}={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}+{\left(\frac{v_h}{\mathrm{\Omega }r}\right)}^{\mathrm{2}}}}}\end{array}$$

with $\tan \mathit{\varphi }=\frac{v_h}{\mathrm{\Omega }r}$. Incremental velocity induced by the vortex element

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\delta }\stackrel{\mathrm{̃}}{\mathit{u}}={\displaystyle \frac{\mathrm{\Delta }\mathrm{\Gamma }}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{\mathit{\delta }\mathit{l}\times \mathit{x}}{|\mathit{x}{|}^{\mathrm{3}}}}=\\ \text{(A4)}& {\displaystyle }& {\displaystyle }Ar\left(\begin{array}{c}\left(v_h/\mathrm{\Omega }r\right)\left(\mathit{\beta }\cos \mathit{\beta }-\sin \mathit{\beta }\right)\\ -\left(v_h/\mathrm{\Omega }r\right)\left(-\mathrm{1}+h_r+\cos \mathit{\beta }+\mathit{\beta }\sin \mathit{\beta }\right)\\ \left[-\mathrm{1}+\left(\mathrm{1}-h_r\right)\cos \mathit{\beta }\right]\end{array}\right),\end{array}$$

with

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }A={\displaystyle \frac{\mathrm{\Delta }\mathrm{\Gamma }r\mathit{\delta }\mathit{\beta }}{\mathrm{4}\mathit{\pi }}}\\ {\displaystyle }& {\displaystyle }{\underset{|\mathit{x}{|}^{\mathrm{2}}}{\underbrace{\left[r^{\mathrm{2}}\left(\mathrm{1}+{\left(\mathrm{1}-h_r\right)}^{\mathrm{2}}-\mathrm{2}\left(\mathrm{1}-h_r\right)\cos \mathit{\beta }+{\left({\displaystyle \frac{v_h\mathit{\beta }}{\mathrm{\Omega }r}}\right)}^{\mathrm{2}}\right)\right]}}}^{-\frac{\mathrm{3}}{\mathrm{2}}}\\ \text{(A5)}& {\displaystyle }& {\displaystyle }{h}_r={\displaystyle \frac{h}{r}}.\end{array}$$