Development of a second-order dynamic stall model

Dynamic stall phenomena carry the risk of negative damping and instability in wind turbine blades. It is crucial to model these phenomena accurately to reduce inaccuracies in predicting design driving (fatigue and extreme) loads. Some of the inaccuracies in current dynamic stall models may be due to the fact that they are not properly designed for high angles of attack and that they do not specifically describe vortex shedding behaviour. The Snel second-order dynamic stall model attempts to explicitly model unsteady vortex shedding. This model could therefore be a valuable addition to a turbine design software such as Bladed. In this paper the model has been validated with oscillating aerofoil experiments, and improvements have been proposed for reducing inaccuracies. The proposed changes led to an overall reduction in error between the model and experimental data. Furthermore the vibration frequency prediction improved significantly. The improved model has been implemented in Bladed and tested against small-scale turbine experiments at parked conditions. At high angles of attack the model looks promising for reducing mismatches between predicted and measured (fatigue and extreme) loading, leading to possible lower safety factors for design and more cost-efficient designs for future wind turbines.

1 Introduction

Wind turbines operate in highly unsteady aerodynamic environments (Leishman, 2002). For design and certification, design load cases (DLCs) have been set which describe the conditions that wind turbine designs have to withstand (DNV GL, 2016). Some of the design driving DLCs are those for parked and idling conditions where wind turbine blades will experience high angles of attack (AoAs), leading to (dynamic) stall behaviour (Schreck et al., 2000). The wind turbine yaw angle is defined as the angle in the horizontal plane between the free-stream wind direction and the wind turbine rotor shaft. It can be noted that when the turbine is parked, and the blades are pitched to 90^∘, the yaw angle effectively becomes the inflow angle. When the yaw system is not operating during parked conditions due to a failure, the blades will experience flow from all directions. For particular wind directions the flow on the blades is separated, leading to dynamic stall effects. These effects may already appear at inflow angles of below 30 and 20^∘ (Gonzalez and Munduate, 2007). Therefore, accurate modelling of dynamic stall is therefore crucial in wind turbine design (Choudry et al., 2014).

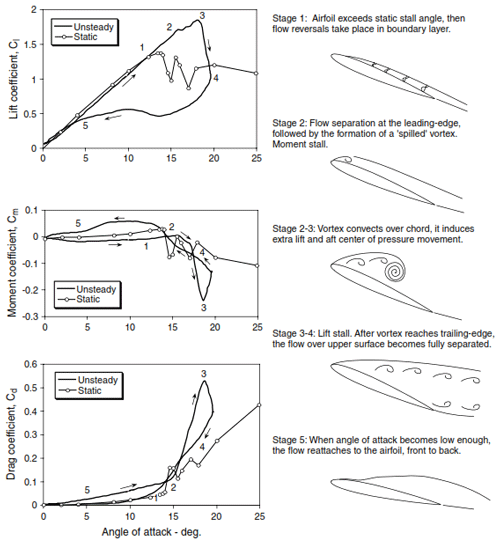
Dynamic stall is a phenomenon leading to larger variations in lift, drag, and pitching moments on the aerofoil than would be observed during steady operation (Choudry et al., 2014). This then creates larger aerodynamic forces on the blades than expected during steady conditions (Leishman, 2002). Dynamic stall happens with dynamic variation in the inflow and/or the effective angle of attack and can be viewed as a delay in the onset of stall. Recirculation of flow after the static stall angle starts near the trailing edge and rapidly moves towards the leading edge, leading to the formation of a large dynamic stall clockwise vortex at the leading edge at increasing angles of attack. The dynamic stall vortex will travel along the suction side, leading towards the trailing edge before detaching completely. Full separation will occur when the dynamic stall vortex is completely detached. This moment is called the “break” or “dynamic stall onset”. As a result, low lift remains until reattachment of the flow. However, a time delay for reattachment of the flow is present as well. After reattachment the process repeats, creating a hysteresis loop. Dynamic stall phenomena carry the risk of negative damping and instability, especially if the aerofoil is oscillating in and out of stall (McCroskey, 1981). A visual description for dynamic stall is presented in Fig. 1.

Figure 1 Classical visual representation of dynamic stall (Leishman, 2002).

When keeping the aerofoil pitched in (deep) stall for longer periods of time, periodic vortex shedding will occur. A single large dynamic stall vortex will no longer be shed, but rather multiple periodic vortices from both the leading and trailing edge will be shed. This will induce time-varying loads on the blades (Riziotis et al., 2010). The periodic vortex shedding is characterized by the Strouhal number representing the dimensionless frequency of shedding (Pellegrino and Meskell, 2013). The Strouhal number is defined following Eq. (1):

$$\begin{array}{}\text{(1)}& St={\displaystyle \frac{f\cdot c}{U}},\end{array}$$

in which f notes the characteristic vortex shedding frequency, c the aerofoil chord (sometimes the projected chord length perpendicular to the incoming flow), and U the wind velocity at the wind turbine blade section. Synchronization of the natural and Strouhal frequencies (a “lock-in”) will lead to resonance (Pellegrino and Meskell, 2013). Locked-in vortex-induced vibrations are a potential threat in standstill conditions as the turbine size is increasing. Modern aeroelastic tools with dynamic stall models are only able to provide accurate deep stall loads at conditions close to maximal lift, so relatively small angles of attack (Riziotis et al., 2010). The same study noted that today's aeroelastic tools are not properly tuned for high angles of attack. Mismatches between load predictions between measurements and engineering tools have been found to be as high as 20 % for high-wind-speed dynamic stall conditions (Schreck, 2002). State-of-the-art aerodynamic models overestimate fatigue loading by 15 % (Schepers and Snel, 2007). Madsen et al. (2019) show promise for using computational fluid dynamics (CFD) in early stages of wind turbine design and shape optimization, and Sørensen et al. (2016) showed that CFD models had good agreement with instrumented rotor experiments. So although CFD is becoming more available and useful in wind turbine design, it requires large computational power. Therefore these tools are not yet fit for practical design calculations. In the industry there is a need for relatively fast and accurate engineering models predicting key loading. Hollierhoek et al. (2013) studied different dynamic stall models, namely Beddoes–Leishman, ONERA, and Snel models. However, a clear single best model was not found. Gonzalez and Munduate (2007) and Wala et al. (2018) both showed promising results using modified and optimized Beddoes–Leishman models compared with experimental data. Inaccuracies in dynamic stall models may be due to the above-described fact that they are not properly designed for high angles of attack and that there are some of them that do not specifically describe vortex shedding behaviour. The Snel second-order dynamic stall model does attempt to explicitly model unsteady vortex shedding. However, there is still the need for further tuning and validation of the model (Snel, 1997). Snel takes the model from Truong (1993) as a starting point. Truong (2017) already showed promise by modifying his model for unsteady vortex shedding, and Snel takes a similar approach. However, as described in Sect. 2, the Snel model differs from the Truong model by incorporating the steady lift coefficient and is therefore interesting to study and modify. This paper will provide a detailed analysis of the Snel second-order model and will try to answer the following main research question:
what are possible ways to improve predictions of blade vibrations during dynamic stall in parked conditions using the Snel second-order model?

This paper will have the following outline.

• The Snel model is validated against experimental data.

• Proposed changes are presented based on the validation results to improve the model predictions. These include a dimensional analysis, calculation of the slope for the potential lift coefficient, application of the normal force coefficient, an investigation into the downstroke and vortex shedding predictions of the model, and finally an optimization for empirical constants.

• Attention will be paid to vibration prediction as this influences turbine fatigue loading, which has a large impact on the design of the wind turbine.

• An absolute error analysis is carried out before and after the improvements to quantify the increase in performance.

• The improved model will be tested with actual small-scale turbine experimental data to assess performance in combination with Bladed.

2 Analysis and validation of the Snel second-order model

This section will validate the Snel model and propose adaptations to the model to improve the performance. The description of the model is based on the description in both Snel (1997) and Hollierhoek et al. (2013). Snel (1997) derived a dynamic stall model based on the work of Truong (1993), who proposed that the dynamic lift coefficient can be distinguished into two parts, namely $\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{1}}}$ and $\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}$:

$$\begin{array}{}\text{(2)}& c_{\mathrm{l},\mathrm{dyn}}=c_{\mathrm{l},\mathrm{steady}}+\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{1}}}+\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}.\end{array}$$

The first describes the forcing frequency response and the second term the self-exited higher-frequency dynamics. Snel follows this approach but also expresses the first part as the difference from the steady-state (time-averaged) lift coefficient (Montgomerie, 1996). The dynamic lift of the Snel model will be as in Eq. (2). The first part, $\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{1}}}$, must decay to zero when no excitation is present, while the second part will decay to zero for small angles of attack, but nearing stall the second part will show periodic oscillations related to vortex shedding.

In the original model of Truong the first part is based on the Beddoes–Leishman dynamic stall model. The Snel model uses the SIMPLE model from Montgomerie (1996) as a departure point for the first-order correction while Truong (1993) uses the Beddoes–Leishman (B–L) model to calculate $\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{1}}}$. The modelling of the first part will therefore follow

$$\begin{array}{}\text{(3)}& \mathit{\tau }\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{1}}}+{\mathrm{cf}}_{\mathrm{10}}\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{1}}}={\mathrm{ft}}_{\mathrm{1}}.\end{array}$$

The forcing term ft₁ will be based on the time derivative of the difference between the steady and potential lift coefficients. This is shown in Eqs. (4) and (5). The function is made non-dimensional by taking the coefficient of the derivative term as the time constant usually used in dynamic stall. This constant is described in Eq. (11).

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }{\mathrm{ft}}_{\mathrm{1}}=\mathit{\tau }\mathrm{\Delta }{\dot{c}}_{\mathrm{l},\mathrm{pot}}\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}=c_{\mathrm{l},\mathrm{pot}}-c_{\mathrm{l},\mathrm{steady}}=\mathrm{2}\mathit{\pi }\sin \left(\mathit{\alpha }-{\mathit{\alpha }}_{\mathrm{0}}\right)-c_{\mathrm{l},\mathrm{steady}}\end{array}$$

The coefficient of $\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{1}}}$ can be seen as a spring trying to pull the term back to the steady state. The stiffness of the spring of this equation is given by Eq. (6). In downwards pitching motion the stiffness is higher than in upwards pitching motion.

$$\begin{array}{}\text{(6)}& {\mathrm{cf}}_{\mathrm{10}}=\left\{\begin{array}{ll}\frac{\mathrm{1}+\mathrm{0.5}\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}}{\mathrm{8}(\mathrm{1}+\mathrm{60}\mathit{\tau }\dot{\mathit{\alpha }})}& \mathrm{if}\dot{\mathit{\alpha }}{c}_{\mathrm{l},\mathrm{pot}}\le \mathrm{0}\\ \frac{\mathrm{1}+\mathrm{0.5}\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}}{\mathrm{8}(\mathrm{1}+\mathrm{80}\mathit{\tau }\dot{\mathit{\alpha }})}& \mathrm{if}\dot{\mathit{\alpha }}{c}_{\mathrm{l},\mathrm{pot}}>\mathrm{0}\end{array}\right.\end{array}$$

The second part of the dynamic lift coefficient is of the second order to create the higher-frequency dynamics. This will be a non-linear mass–damper–spring system following

$$\begin{array}{}\text{(7)}& {\mathit{\tau }}^{\mathrm{2}}\mathrm{\Delta }{\ddot{c}}_{{\mathrm{l}}_{\mathrm{2}}}+{\mathrm{cf}}_{\mathrm{21}}\mathrm{\Delta }{\dot{c}}_{{\mathrm{l}}_{\mathrm{2}}}+{\mathrm{cf}}_{\mathrm{20}}\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}={\mathrm{ft}}_{\mathrm{2}}.\end{array}$$

The spring and damping coefficients are taken from Snel (1997) and are defined as in Eqs. (8) and (9) respectively.

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathrm{cf}}_{\mathrm{20}}=k_{\mathrm{s}}^{\mathrm{2}}\left[\mathrm{1}+\mathrm{3}{\left(\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]\left[\mathrm{1}+\mathrm{3}{\dot{\mathit{\alpha }}}^{\mathrm{2}}\right]\text{(9)}& {\displaystyle }\begin{array}{rl}& {\mathrm{cf}}_{\mathrm{21}}=\\ & \left\{\begin{array}{ll}\mathrm{60}\mathit{\tau }{k}_{\mathrm{s}}\left[-\mathrm{0.01}\left(\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}-\mathrm{0.5}\right)+\mathrm{2}{\left(\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]& \mathrm{if}\dot{\mathit{\alpha }}>\mathrm{0}\\ \mathrm{2}\mathit{\tau }{k}_{\mathrm{s}}& \mathrm{if}\dot{\mathit{\alpha }}\le \mathrm{0}\end{array}\right.\end{array}\end{array}$$

Also, here it can be noted that the response will be different in pitching upwards or downwards. The forcing term is defined as

$$\begin{array}{}\text{(10)}& {\mathrm{ft}}_{\mathrm{2}}=\mathrm{0.1}{k}_{\mathrm{s}}\left(-\mathrm{0.15}\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}+\mathrm{0.05}\mathrm{\Delta }{\dot{c}}_{\mathrm{l},\mathrm{pot}}\right).\end{array}$$

In the second-order part of the model, k_s is taken as the reduced vortex shedding frequency or Strouhal number. This is given a value of 0.2 as in the original model (Snel, 1997). In the above equations the time constant is given below and can be seen as the time it takes for the wind to travel half a chord distance:

$$\begin{array}{}\text{(11)}& \mathit{\tau }=c/\mathrm{2}U.\end{array}$$

2.1 Initial model implementation and validation

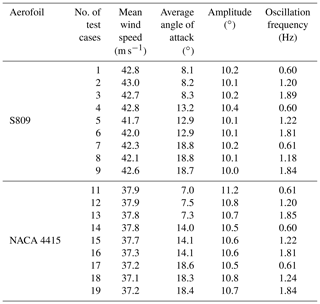
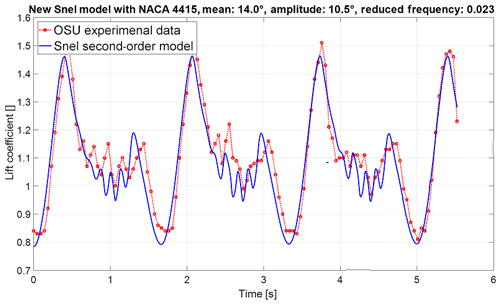
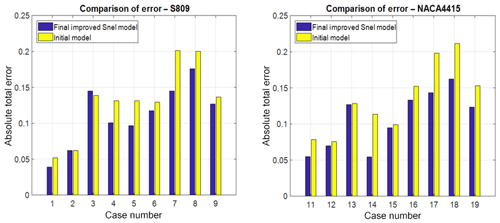
The Snel model as described in the section above is implemented in a MATLAB environment. The numerical implementation follows the steps described in De Vaal (2009). The time step used is 0.001 s to capture higher-frequency events from the Ohio State University experiments. The Ohio State University (OSU) experiments (Hoffmann et al., 1996) will be used for validation of the initial implementation of the Snel model. In the OSU experiments an extensive set of aerofoils have been tested for both unsteady and steady data. The measurements recorded responses to forced sinusoidal pitching oscillations. Different amplitudes, mean angles of attack, oscillation frequencies, and Reynolds numbers were tested. The focus in this paper will be on the NACA4415 and S809 aerofoils. The model parameters obtained from the OSU database, as displayed in Table 1, will be analysed. The oscillation frequencies of the cases are set such that the forcing angle of attack matches the OSU experiments. Figures 2 and 3 show the time series of the lift coefficient for cases with both low and high reduced frequencies and low and high mean angles of attack. The following observations can been made for the current model:

• The current model overpredicts the loss of lift during the downstroke.

• The predicted vortex shedding does not always happen at the correct time.

• There is currently no unsteady vortex shedding at higher angles of attack.

• The shedding frequency is not dependent on the reduced frequency while the experiments do show a dependency.

These points will be analysed as part of the possible improvements described in Sect. 3.3 up to Sect. 3.9.

Table 1 Selected cases from the OSU experiments.

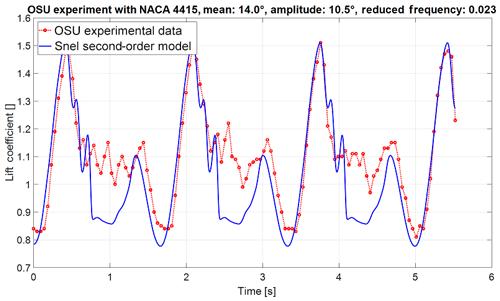
Figure 2 Lift coefficient time of the initial Snel model (NACA 4415 aerofoil with mean angle of attack of 14^∘, amplitude of 10.5^∘, and reduced frequency of 0.023).

Figure 3 Lift coefficient time of the initial Snel model (NACA 4415 aerofoil with mean angle of attack of 18.4^∘, amplitude of 10.7^∘, and reduced frequency of 0.071).

2.2 Error analysis

To quantify the accuracy of the Snel model, the total absolute error between model predictions and experimental data is calculated. This will give an objective measure to assess proposed improvements. The Snel model is interpolated along the angle of attack to obtain the dynamic lift coefficient output at the precise angles of attack of the OSU experiment. The errors are then evaluated according to

$$\begin{array}{}\text{(12)}& E_i=c_{\mathrm{l},\mathrm{model}}\left({\mathit{\alpha }}_i\right)-c_{\mathrm{l},\mathrm{OSU}}\left({\mathit{\alpha }}_i\right),\end{array}$$

and the total absolute error of all data points is calculated using

$$\begin{array}{}\text{(13)}& \mathrm{absolute}\mathrm{error}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{E}_i^{\mathrm{2}}},\end{array}$$

in which n denotes the number of data points of the OSU experimental data.

3 Proposed changes to the Snel model

This section will outline proposed modifications to the Snel model. The following areas will be investigated for modification:

• a dimensional analysis of the model,

• the calculation method of the slope for the potential lift coefficient,

• application of the normal force coefficient instead of the lift force coefficient,

• the downstroke prediction of the model,

• prediction of vortex shedding,

• and lastly an optimization for empirical (aerofoil-specific) constants.

3.1 Dimensional analysis

It can be seen in the formulation of the model that Eqs. (8) and (10) are cast in a dimensional form. For different values for chords, wind speed, and pitching frequency, the current model will not produce identical results. In order to make them dimensionless, the time constant used in dynamic stall (Eq. 11) is added. The new constants will be such that the initial value of the constant is kept. The equations will now be

$$\begin{array}{}\text{(14)}& {\displaystyle }& {\displaystyle }{\mathrm{cf}}_{\mathrm{20}}=k_{\mathrm{s}}^{\mathrm{2}}\left[\mathrm{1}+\mathrm{3}{\left(\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]\left[\mathrm{1}+{\mathrm{280}}^{\mathrm{2}}{\mathit{\tau }}^{\mathrm{2}}{\dot{\mathit{\alpha }}}^{\mathrm{2}}\right],\text{(15)}& {\displaystyle }& {\displaystyle }{\mathrm{ft}}_{\mathrm{2}}=\mathrm{0.1}{k}_{\mathrm{s}}\left(-\mathrm{0.15}\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}+\mathrm{8}\mathit{\tau }\mathrm{\Delta }{\dot{c}}_{\mathrm{l},\mathrm{pot}}\right).\end{array}$$

Figure 4 Steady polars of the NACA 4415 aerofoil.

3.2 Correct slope for Cl potential

The Snel model uses 2π as theoretical slope for lift coefficient at low angles of attack. This theoretical value might not be applicable to real aerofoils. Calculating the precise slope improves the accuracy of the model. Therefore the slope calculated from the aerofoil polar is used in the model. The slope is calculated between the intercept at angle of attack = 0 and the intercept at lift coefficient = 0.

3.3 Application of the normal force coefficient

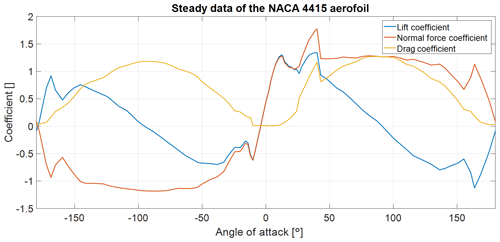
The Snel model uses the lift coefficient of the steady aerofoil data. However, the lift coefficient tends to zero when angles of attack reach 90^∘. At a 90^∘ angle of attack there is still unsteady vortex shedding present. Therefore, it would make sense to model vortex shedding to the normal force on the aerofoil instead of the lift force. The normal force coefficient together with the lift and drag coefficients are presented in Fig. 4. For implementation all the C_L terms are changed to C_n terms. A couple of additions must then be made to the model to obtain the dynamic lift and drag coefficients. First, the steady normal force coefficient (c_n,steady) is the sum of the steady lift and drag coefficient and the angle of attack following

$$\begin{array}{}\text{(16)}& c_{\mathrm{n},\mathrm{steady}}=c_{\mathrm{l},\mathrm{steady}}\cos \left(\mathit{\alpha }\right)+c_{\mathrm{d},\mathrm{steady}}\sin \left(\mathit{\alpha }\right),\end{array}$$

and the steady chordwise coefficient (c_c,steady) will follow

$$\begin{array}{}\text{(17)}& c_{\mathrm{c},\mathrm{steady}}=-c_{\mathrm{l},\mathrm{steady}}\sin \left(\mathit{\alpha }\right)+c_{\mathrm{d},\mathrm{steady}}\cos \left(\mathit{\alpha }\right).\end{array}$$

When the dynamic normal force coefficient has been obtained, an inverse calculation yields the lift and drag coefficients:

$$\begin{array}{}\text{(18)}& {\displaystyle }& {\displaystyle }{c}_{\mathrm{l},\mathrm{dyn}}=c_{\mathrm{n},\mathrm{dyn}}\cos \left(\mathit{\alpha }\right)-C_{\mathrm{c},\mathrm{steady}}\sin \left(\mathit{\alpha }\right),\text{(19)}& {\displaystyle }& {\displaystyle }{c}_{\mathrm{d},\mathrm{dyn}}=c_{\mathrm{n},\mathrm{dyn}}\sin \left(\mathit{\alpha }\right)+C_{\mathrm{c},\mathrm{steady}}\cos \left(\mathit{\alpha }\right).\end{array}$$

3.4 Downstroke of the model

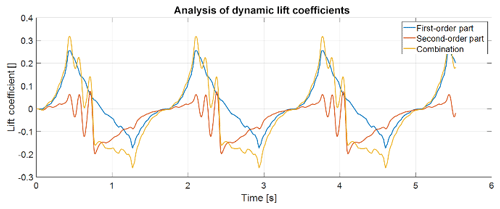
The consistent differences between the implementation of the Snel second-order model and earlier implementations are lower values in the downstroke. Figure 5 shows the first- and second-order part of the model as a function of time. The second-order part ($\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}$) contributes highly to the lower values at the start of the downstroke, which causes a large part of the observed error.

Figure 5 Analysis of the dynamic lift coefficient.

Equation (10) uses $-\mathrm{0.15}\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}$. Together with a negative $\mathrm{\Delta }{\dot{c}}_{\mathrm{l},\mathrm{pot}}$ in the downstroke, ft₂ will be highly negative in the downstroke. To improve this behaviour the forcing term is set to zero for the downstroke. In addition, Figs. 2 and 3 show that the predicted shedding in the upstroke is larger than in the measurements. Therefore, the forcing term is lowered and will be changed to

$$\begin{array}{}\text{(20)}& {\mathrm{ft}}_{\mathrm{2}}=\mathrm{0.1}{k}_{\mathrm{s}}\left(-\mathrm{0.08}\mathrm{\Delta }{c}_{\mathrm{l},\mathrm{pot}}+\mathrm{1.5}\mathit{\tau }\mathrm{\Delta }{\dot{c}}_{\mathrm{l},\mathrm{pot}}\right).\end{array}$$

From Figs. 1 and 2 it is visible that there are higher frequencies in the downstroke. This is not modelled as cf₂₁ is a constant value in the downstroke; see Eq. (9). To allow shedding, the coefficient is changed to

$$\begin{array}{}\text{(21)}& \begin{array}{rl}& {\mathrm{cf}}_{\mathrm{21}}=\\ & \left\{\begin{array}{ll}\mathrm{60}\mathit{\tau }{k}_{\mathrm{s}}\left[-\mathrm{0.01}\left(\mathrm{\Delta }{c}_{\mathrm{n},\mathrm{pot}}-\mathrm{0.5}\right)+\mathrm{2}{\left(\mathrm{\Delta }{c}_{{\mathrm{n}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]& \mathrm{if}\dot{\mathit{\alpha }}>\mathrm{0}\\ \mathrm{60}\mathit{\tau }{k}_{\mathrm{s}}\left[-\mathrm{0.01}\left(\mathrm{\Delta }{c}_{\mathrm{n},\mathrm{pot}}-\mathrm{0.5}\right)+\mathrm{12}{\left(\mathrm{\Delta }{c}_{{\mathrm{n}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]& \mathrm{if}\dot{\mathit{\alpha }}\le \mathrm{0}\end{array}\right..\end{array}\end{array}$$

The damping in the downstroke is set higher than in the upstroke.

Table 2 Constants used for optimization.

3.5 Prediction of vortex shedding

The shedding frequency will depend on the angle of attack. The current model does not predict a dependency and so it has to be improved in this aspect. The Strouhal number uses the chord or the projected chord perpendicular to the incoming flow. Because the projected chord length is driven by the angle of attack, it is proposed to add the projected chord length to the “spring” term (cf₂₀) of the second-order part. This allows for the desired dependency of stiffness. From Eq. (1) it can be inferred that when projecting the chord perpendicular to the incoming flow this is effectively the same as projecting the Strouhal number. The new equation for cf₂₀ will now be

$$\begin{array}{}\text{(22)}& {\mathrm{cf}}_{\mathrm{20}}=\mathrm{10}\cdot k_{\mathrm{s},\mathrm{pr}}^{\mathrm{2}}\left[\mathrm{1}+\mathrm{3}{\left(\mathrm{\Delta }{c}_{{\mathrm{l}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]\left[\mathrm{1}+{\mathrm{280}}^{\mathrm{2}}{\mathit{\tau }}^{\mathrm{2}}{\dot{\mathit{\alpha }}}^{\mathrm{2}}\right],\end{array}$$

with

$$\begin{array}{}\text{(23)}& k_{\mathrm{s},\mathrm{pr}}=k_{\mathrm{s}}\cdot \sin \left(\mathit{\alpha }\right).\end{array}$$

Figure 6 Absolute error analysis of the optimization runs for all cases from Table 1.

Figure 7 Lift coefficient over time of the improved Snel model (NACA 4415 aerofoil with mean angle of attack of 14^∘, amplitude of 10.5^∘, and reduced frequency of 0.023).

3.6 Optimization for (aerofoil-specific) constants

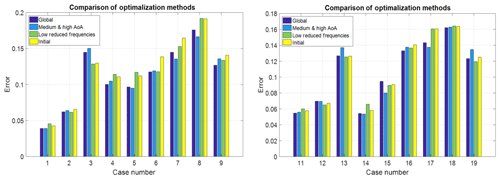
An unconstrained minimization algorithm in MATLAB is used to optimize empirical constants. The algorithm searches for the lowest summation of the absolute errors, from Eq. (13), of all cases considered. The constants selected for this analysis are shown in the initial row of Table 2. The constants are selected since they are included in equations affected by the modifications from this section and also because they have a high influence on the output of the Snel model. Three optimization analyses have been carried out: a global optimization which covers all cases, an optimization which focussed only on the cases with a mean angle of attack of 14 or 20^∘, and an optimization on the low-reduced-frequency cases. The initial constants as in Table 2 are the start values for the optimization. The results for all individual cases, using the error analysis described in Sect. 2.2, are shown in Fig. 6. It can be seen that the global optimization is the most optimal. The global optimization gives the most consistently lower error compared to the initial model. In Bladed the Beddoes–Leishman dynamic stall model has three sensitive constants which are allowed to be changed by the user. For the Snel model, the optimization shows that two constants are the most sensitive. The optimization output showed significantly different values for these constants for the NACA 4415 and the S809 aerofoils. They are shown in the improved row of Table 2. These constants must be allowed to be changed by users of a turbine design code. The same goes for the Strouhal number. The constants are

• C1 from Table 2, which will be called the first-order coefficient and

• C2 from Table 2, which will be called the second-order forcing coefficient.

As a result of this optimization step the following changes are implemented. Equation (6) will change to

$$\begin{array}{}\text{(24)}& {\mathrm{cf}}_{\mathrm{10}}=\left\{\begin{array}{ll}\frac{\mathrm{1}+C_{\mathrm{1}}\cdot \mathrm{\Delta }{c}_{\mathrm{n},\mathrm{pot}}}{\mathrm{8}(\mathrm{1}+\mathrm{60}\mathit{\tau }\dot{\mathit{\alpha }})}& \mathrm{if}\dot{\mathit{\alpha }}{c}_{\mathrm{n},\mathrm{pot}}\le \mathrm{0}\\ \frac{\mathrm{1}+C_{\mathrm{1}}\cdot \mathrm{\Delta }{c}_{\mathrm{n},\mathrm{pot}}}{\mathrm{8}(\mathrm{1}+\mathrm{80}\mathit{\tau }\dot{\mathit{\alpha }})}& \mathrm{if}\dot{\mathit{\alpha }}{c}_{\mathrm{n},\mathrm{pot}}>\mathrm{0}\end{array}\right..\end{array}$$

Equation (20) will change to

$$\begin{array}{}\text{(25)}& {\mathrm{ft}}_{\mathrm{2}}=\mathrm{0.01}{k}_{\mathrm{s}}\left(-\mathrm{0.04}\mathrm{\Delta }{c}_{\mathrm{n},\mathrm{pot}}+C_{\mathrm{2}}\mathit{\tau }\dot{\mathrm{\Delta }}{c}_{\mathrm{n},\mathrm{pot}}\right).\end{array}$$

The first-order coefficient C₁ will be 0.5 for the NACA 4415 aerofoil and 0.2 for the S809. For the second-order forcing coefficient C₂ will be 1 and 1.5 respectively. Table 2 shows that for Eqs. (18) and (19) the constants remain the same. Therefore these remain unchanged. Finally Eq. (21) will become as follows:

$$\begin{array}{}\text{(26)}& \begin{array}{rl}& {\mathrm{cf}}_{\mathrm{21}}=\\ & \left\{\begin{array}{ll}\mathrm{60}\mathit{\tau }{k}_{\mathrm{s}}\left[-\mathrm{0.01}\left(\mathrm{\Delta }{c}_{\mathrm{n},\mathrm{pot}}-\mathrm{0.5}\right)+\mathrm{2}{\left(\mathrm{\Delta }{c}_{{\mathrm{n}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]& \mathrm{if}\dot{\mathit{\alpha }}>\mathrm{0}\\ \mathrm{60}\mathit{\tau }{k}_{\mathrm{s}}\left[-\mathrm{0.01}\left(\mathrm{\Delta }{c}_{\mathrm{n},\mathrm{pot}}-\mathrm{0.5}\right)+\mathrm{14}{\left(\mathrm{\Delta }{c}_{{\mathrm{n}}_{\mathrm{2}}}\right)}^{\mathrm{2}}\right]& \mathrm{if}\dot{\mathit{\alpha }}\le \mathrm{0}\end{array}\right..\end{array}\end{array}$$

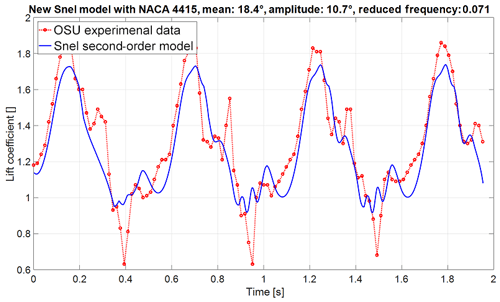
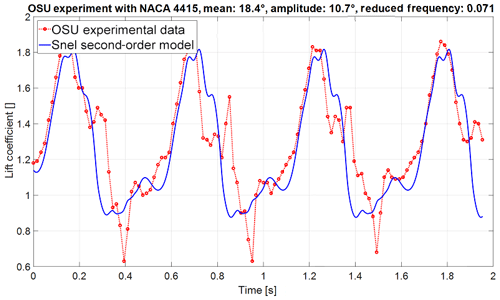
Figure 8 Lift coefficient over time of the improved Snel model (NACA 4415 aerofoil with mean angle of attack of 18.4^∘, amplitude of 10.7^∘, and reduced frequency of 0.071).

Figure 9 Lift coefficient over time of the improved Snel model (S809 aerofoil with mean angle of attack of 18.8^∘, amplitude of 10.2^∘, and reduced frequency of 0.021).

4 Results of the proposed modifications

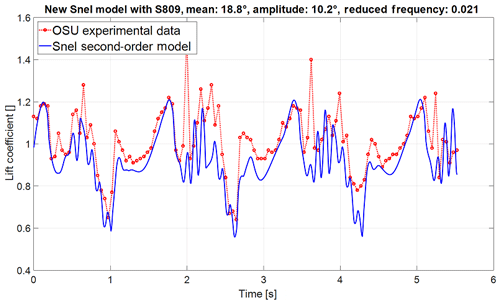
The modified Snel model is implemented as described in Sect. 2.1 and tested against the same set of experiments as in Table 1. The results of the modified Snel model are shown in Figs. 7 and 8. In comparison to Figs. 2 and 3 it is noted that the shedding prediction at low reduced frequency is improved. For the higher reduced frequency the model also captures the shedding slightly better, even though there is less shedding present. Furthermore, it can be seen that the frequency changes between both cases as desired. It is important to investigate the impact changes on different situations and aerofoils. Figure 9 displays the updated model in combination with the S809 aerofoil. The improved model still predicts slightly lower values than the experiments but the overall trends are followed nicely, and shedding frequency matches the experiment well.

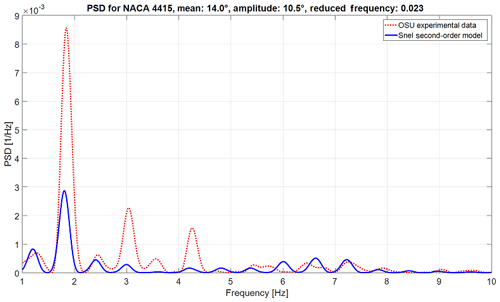
Figure 10 Power spectral density of experimental data and the improved Snel model (NACA 4415 aerofoil mean angle of attack of 14^∘, amplitude of 10.5^∘, and reduced frequency of 0.023).

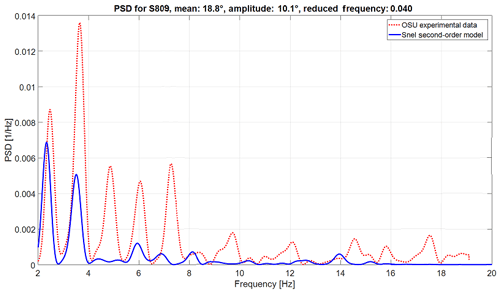
Figure 11 Power spectral density of experimental data and the improved Snel model (S809 aerofoil with mean angle of attack of 18.8^∘, amplitude of 10.1^∘, and reduced frequency of 0.040).

Another goal of the proposed changes to the Snel model was to capture, predict, and match the vortex shedding and the shedding frequency of aerofoils in dynamic stall conditions. In order to check the validity of these changes in a quantitative way, a frequency domain analysis has been performed. The power spectral density (PSD) estimate is calculated using Welch's method. The Hamming window is set equal to the number of data points and the number of overlapped values to 50 % of the window length. The forcing frequency is removed from the plot as the shedding frequencies are higher and the forcing frequency will take up a large proportion of the PSD. The results for both aerofoils are shown in Figs. 10 and 11. From the figures it becomes clear that the Snel model captures, for both aerofoils at different mean angles of attack and different reduced frequencies, the self-induced shedding frequencies fairly correct. However, as shown in Figs. 7–9, there is still room for improvement here. All predicted shedding frequencies match frequencies observed in the measurements, whereas the intensity is not always correct. Care must be taken with the higher frequencies as the OSU measurement has a relatively low sampling frequency and might therefore not fully capture some higher-frequency dynamics.

Figure 12 Comparison of the total absolute error of both the initial and improved Snel models.

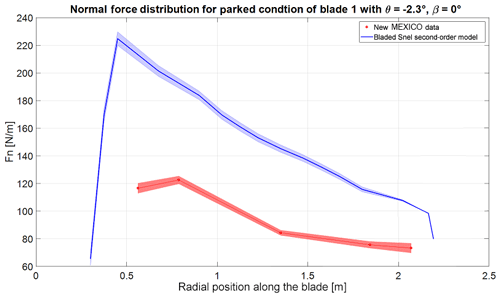
Figure 13 Normal force distribution of the blade at 0^∘ azimuth with −2.3^∘ pitch and 0^∘ wind direction. The bold line represents the mean value, and the shaded area is the standard deviation.

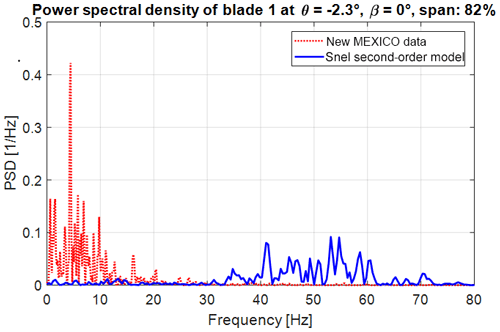
Figure 14 Power spectral density at 82 % span of the blade at 0^∘ azimuth with −2.3^∘ pitch and 0^∘ wind direction.

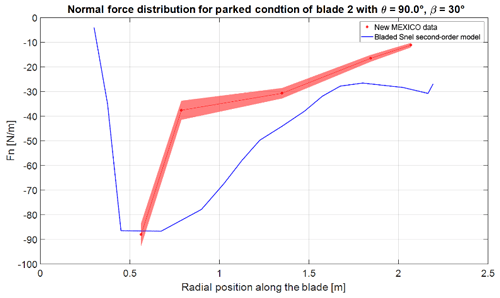
Figure 15 Normal force distribution of the blade at 120^∘ azimuth with 90^∘ pitch and 30^∘ wind direction. The bold line represents the mean value and the shaded area the standard deviation.

To quantify the improvements, the effects of all previous changes on the overall absolute error of the new model are shown in Fig. 12 together with the overall error of the initial model of Sect. 3. It is seen that the improved model outperforms the initial model in almost every case with a single exception. The initial model already gave very accurate results for that case, and the increase in error is very small compared to the reduction achieved in all other cases. It is also noted that the overall prediction of the shedding phenomena has been improved. Hence it can be concluded that the model changes developed and presented in this paper improve the performance of the Snel second-order model.

5 The updated Snel model performance with New MEXICO data

Model Experiments In Controlled Conditions (MEXICO) was a project in which an instrumented, three-bladed turbine of 4.5 m rotor diameter was tested (Schepers et al., 2012). MEXICO was carried out in the Large Low-Speed Facility (LLF) of the German-Dutch Wind Tunnels (DNW) (Schepers et al., 2012). The blades were fitted with pressure sensors at 25 %, 35 %, 60 %, 82 %, and 92 % radial positions. Tests were performed with 30 m s⁻¹ wind speed, blades pitched to vane, and yaw inflow angles in the range of −90 to 30^∘ and for three azimuthal positions (0, 120, and 240^∘). This data set is particularly valuable for the testing of dynamic stall models as it represents standard load cases set out by the IEC (DNV GL, 2016). For a complete overview of the MEXICO and New MEXICO projects, reference is made to Schepers et al. (2012). Khan (2018) conducted similar research with different dynamic stall models, and their study will be used as a baseline in this paper. The improved Snel model from this paper will be tested against the New MEXICO data sets of Table 3 (β = wind direction, θ = pitch angle) to see if the additions and changes to the model have a positive influence on the accuracy. The blade geometry, mass, and flexibility distribution are modelled in Bladed according to New MEXICO data. The modal damping in the calculations is set to 0.5 %. In the runs the rotational augmentation is turned off just like in Khan (2018). The tip and root loss Prandtl corrections as well as tower shadow effects are also turned off. A total of 21 blade stations, as in the geometry description of the New MEXICO blade, are used. The starting and ending radii for the dynamic stall model are 25 % and 95 %. The normal force distribution in axial flow, with pitch −2.3^∘ and thus an angle of attack of about 90^∘, is given in Fig. 13. The Snel model shows roughly the same size of normal force fluctuations as in the experiment. Khan (2018) found similar deviations in the mean values of the normal force distributions with different turbine design codes and different dynamic stall models. A reason for this deviation is not mentioned and should be part of further research. The improved Snel model predicts shedding at −2.3^∘ pitch with axial flow, due to the addition of the normal force coefficient, while the original model as in Khan (2018) does not. The PSDs of the time series of both the New MEXICO data and the Bladed output are compared. The normal force time series are standardized by subtracting the mean and dividing by the standard deviation. The Hamming window is set to equal the number of data points and the number of overlapped values to 50 % of the window length. The results are shown in Fig. 14 at the radial location of 82 % of the total span.

The updated Snel model shows significantly higher-frequency vibrations in the normal force of the New MEXICO blade. Figure 15 shows the normal force distribution for the blade at azimuth 120^∘ for the yawed case with 30^∘ wind direction and 90^∘ pitch. Interesting to notice for this case is that the angle of attack will be negative. The Snel model does not show any unsteadiness in the normal force distribution. Further research is needed to explain and improve the Snel model for negative angles of attack.

Table 3 Investigated cases from the New MEXICO experiments.

A single reason for the higher-frequency prediction has not been found. Several possibilities are suggested. First, the modal damping is not specified in the New MEXICO turbine data and was therefore assumed to be 0.5 %. Second, the impact of different aerofoils from the New MEXICO blade is unknown. The first-order or second-order forcing coefficients might require other values. Furthermore, the Strouhal number for the New MEXICO blade is not 0.2 Hz at high angles of attack (Khan, 2018). Research by Skrypinski et al. (2014) and Zou et al. (2015) shows that for aerofoils with an effective angle of attack of around 90^∘ the Strouhal number should be around 0.10–0.13 Hz. This ought to be implemented in the model and tested in further research. Third, wind tunnel effects are not modelled in Bladed. The wind field in Bladed has zero turbulence and wind tunnel effects. More research on the Snel model in Bladed with actual turbine data is advised.

6 Conclusion and recommendations

The Snel model has been validated with OSU experimental data, and following this validation propositions for improvements have been made. The improvements to the model have been tested and led to a reduction in the overall error between the Snel model and the OSU experimental data. Furthermore, an improvement in the prediction of both the amplitude and frequency of vibrations in the measurements has been accomplished. The improved model is implemented in the Bladed turbine design software and tested against the New MEXICO experimental data. Prediction of normal force distributions along the blade seems to match earlier implementations in other turbine design codes while the mean value of the normal force is not correct. This is a major area for further research and improvement. The Snel model predicts the amplitude of the normal force vibrations well while the predicted frequency is higher than in the experiment. A single reason for this has not been found, and therefore further research into the Snel model is advised. Truong (2017) proposed a similar modification of his original model as Snel (1997) and therefore also similar to the model adaptations presented in this paper. The main difference lies in the incorporation of the steady lift data as described in Sect. 2. The authors highly recommend a study comparing both the model described in Truong (2017) and the model presented in this paper. The model as proposed is formulated on the basis of variations in angles of attack. It is recommended for further research to delve into the possibility to adept this model to dynamic variation in inflow velocity for the case of rotating and vibrating blades.

The proposed Snel second-order dynamic stall model might become a valuable addition to the modelling of dynamic behaviour in stall conditions. As the conditions tested in this paper are often design driving, the Snel model looks promising for more accurate prediction of design-driving (fatigue and extreme) loads and more cost-efficient wind turbine designs.