the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Aeroelastic response of a multi-megawatt upwind horizontal axis wind turbine (HAWT) based on fluid–structure interaction simulation
Yasir Shkara
Martin Cardaun
Ralf Schelenz
Georg Jacobs
With the increasing demand for greener, sustainable, and economical energy sources, wind energy has proven to be a potential sustainable source of energy. The trend development of wind turbines tends to increase rotor diameter and tower height to capture more energy. The bigger, lighter, and more flexible structure is more sensitive to smaller excitations. To make sure that the dynamic behavior of the wind turbine structure will not influence the stability of the system and to further optimize the structure, a fully detailed analysis of the entire wind turbine structure is crucial.
Since the fatigue and the excitation of the structure are highly depending on the aerodynamic forces, it is important to take blade–tower interactions into consideration in the design of large-scale wind turbines. In this work, an aeroelastic model that describes the interaction between the blade and the tower of a horizontal axis wind turbine (HAWT) is presented. The high-fidelity fluid–structure interaction (FSI) model is developed by coupling a computational fluid dynamics (CFD) solver with a finite element (FE) solver to investigate the response of a multi-megawatt wind turbine structure. The results of the computational simulation showed that the dynamic response of the tower is highly dependent on the rotor azimuthal position. Furthermore, rotation of the blades in front of the tower causes not only aerodynamic forces on the blades but also a sudden reduction in the rotor aerodynamic torque by 2.3 % three times per revolution.
- Article
(6046 KB) - Full-text XML
- BibTeX
- EndNote
Wind energy is an abundant energy source compared to other traditional energy resources. Today, the multi-megawatt wind turbine is more powerful and more sophisticated than the early versions. Designers have optimized wind turbines, making them more efficient, cheaper, and more competitive in comparison to other renewable energy generators.
It is important that the wind turbine operates in a stable condition to avoid structural vibration. In most cases, the structure absorbs the input energy leading to a decrease in vibration amplitude. However, underestimated or neglected aerodynamics–structure interactions can lead to energized violent vibration that leads to serious structural fatigue damage. Accordingly, the importance of fatigue in the design of a wind turbine is higher than other rotary machines for a lifetime in the range of 20–30 years.
1.1 Horizontal axis wind turbine structure
A horizontal axis wind turbine (HAWT) can be described as a low-stiffness dynamic system which comprises complex interactions between its individual components and the surrounding atmosphere. The wind turbine support structure is a long cylindrical column, where the rotor and the other components are mounted at the top. The importance of the support structure is based on the fact that the tower is the most expensive part of the machine (26 % of the total cost; EWEA Wind Directions, 2007). In addition, the support structure must sustain the loads that occur during the operation and be capable to satisfy the safety of the structure for the designed lifetime.
A tubular tower is designed in two ways: stiff or soft. Stiff towers have a natural frequency higher than the blade-passing frequency; contrarily, soft towers have to endure turbine vibrations that make it suffer from higher stress levels. Due to the variety of dynamic loads that the wind turbine is subjected to (e.g., erratic wind gusts, storms, rotor dynamics), cyclic loads which are three-dimensional in nature are induced. Therefore, the tower structure is sensitive to vibration under various atmospheric conditions and its own dynamics. The design and development trends of the horizontal axis wind turbines is towards low-cost large-scale wind turbines. Increasing the rotor diameter will not just raise the turbine power but doubling wind velocity will boost the power by eight times. For these reasons and in addition to wind shear, it makes sense to increase tower height so that more energy can be captured.
1.2 Challenges associated with large-scale wind turbines
Bigger, lighter, and more flexible wind turbine rotors make the dynamics of the structure more complicated. Scaling up the size of the machine constitutes a challenge. With the increase in wind turbine size, aeroelastic problems have been experienced on some wind turbines. Aeroelastic problems can result in structure collapse; therefore, it is essential that the design of the wind turbine avoids aeroelastic instability. In general, the associated problems with the increasing of turbine size can be summarized as follows.
Higher blade flexibility. The continuing increase in wind turbine blade length makes the latter more flexible. Lighter, flexible blades result in higher deformation, blade fluttering, and alter turbine performance. Blade fluttering increases pitch moment at the blade root and pitching system, and it causes instability problems which reduce the operational life of the wind turbine (Hansen et al., 2006; Ahlstrom, 2006).
Transportation problem. One of the critical problems that faces the multi-megawatt wind turbines is the transportation problem. As the tower gets longer, the tower base diameter increases. Nowadays the dimensions of wind turbine towers have almost reached the limits of European roads (maximum 4 m height; Council Directive 96/53/EC, 1996).
Rotor–tower strike risk. Longer blades need bigger rotor–tower clearance to avoid blade–tower strike. The (International Electrotechnical Commission) IEC 61400-1 states that the blade tower should be at least 1.5 times the blade deflection (IEC 61400-1, 2005). For large wind turbines, rotor–tower clearance is also achieved by shifting the nacelle forward to keep the minimum required safety clearance. However, shifting the nacelle will create additional moment at the tower foundation that must be considered in the tower design.
Installation collapse risk. As the turbine's support structure becomes taller, the risk of its collapse during the installation process becomes higher. Leaving the long tower standing for a long time without completing the assembly of the wind turbine (e.g., due to a delay of the other components or bad weather conditions) increases the risk of tower collapse. The problem also arises when the tower is exposed to certain wind conditions in which the shedding vortex frequencies (known as von Kármán vortices) match with the natural frequency of the tower. In this case, the tower starts to vibrate violently leading to fatigue damage.
Blade–tower interaction. Despite the fact that the effect of blade–tower interaction on an upwind wind turbine is less than a downwind one (Zhao et al., 2014), it is a very complex problem to analyze analytically due to the high-nonlinear behavior of the aerodynamic forces in the system. Chattot (2006) and Shkara et al. (2018) showed in their study that even for upwind wind turbines the tower has a significant effect on the unsteady working conditions of the blades as a result of tower blockage.
The aerodynamic forces on the rotor and the support structure change frequently during the blade's rotation. Therefore, it is necessary to design the turbine structure in such a way that the natural frequency of the system does not interfere with the operating load frequency so that tower resonance can be avoided. According to the Danish Standard DS 472 (2009), simple statical analysis can be used for limited rotor size (up to 25 m or 200–250 kW rated power). For larger wind turbines, accurate aeroelastic models involving detailed flow simulation and structure response are essential (Danish Standard DS 472, 2009; Rauh and Peinke, 2004; Tavner et al., 2007).
1.3 Related literature
Blade–tower interaction has been studied by many researchers with different methods in terms of level of detail and computational cost. The nonlinear vortex correction method with time-marching free wake has been adopted by Kim et al. (2011) to investigate the interaction between the tower and the blade. Their model showed a change in the normal force coefficient by approximately 10 % of the average. They found that the influence of the tower radius variations on the interaction is bigger than tower clearance variations. Tang et al. (2017) developed an aeroelastic method to study the response of a 1.5 MW wind turbine by coupling a multibody method with a free vortex wake (FVW) method. The simulation results indicated that the aeroelasticity of a blade has significant effects on the wake geometries and structural responses. Flexibility of the tower can cause higher power and load fluctuations than the blade, which can considerably affect the blade fatigue life design.
Furthermore, Lackner et al. (2013) investigated blade–tower interaction using potential flow that includes 2-D and 3-D versions. The drawback of their model was the inability to predict the flow field accurately as the flow over the tower encounters some viscous separation causing more complex flow.
On the other hand, Janajreh et al. (2010) performed a 2-D computational fluid dynamics (CFD) simulation of a downwind wind turbine to investigate the blade–tower interaction during the intrinsic passage of the rotor in the wake of the tower. The time history of the pressure, lift, and drag coefficients and the moments were evaluated for three different cross-sectional towers and compared with the panel method. The simulation results showed a reduction between 5 % and 57 % of the aerodynamic lift forces during blade passage in the wake of the symmetrical airfoil tower. Following the same concept, the 2-D simulation by Gomez and Seume (2009) of an upwind wind turbine showed a change in the stagnation point and the vortex separation points on the tower three times per revolution. The 3-D CFD simulation of Wang et al. (2012) showed a small influence of the tower on the aerodynamic performance of an upwind wind turbine. Results indicated that rotation of the blades in front of the tower will induce an obvious cyclic pressure drop and a noticeable flow separation from the tower due to the strong blade-tip vortices.
Hsu and Bazilevs (2012) performed a 3-D fluid–structure interaction (FSI) simulation of full-scale upwind wind turbines. In their model the interaction between the flexible rotor and the rigid tower of the three-blade 5 MW wind turbine showed a blade aerodynamic torque drop of 10 %–12 % when it passes by the tower. In addition, a blade-tip fluctuation of about 1 m is noticed. Moreover, the full CFD-CSD (computational fluid dynamics and computational structural dynamics) model of Carrion et al. (2014) showed that, due to the proximity of the rotor to the tower, a deficit on the thrust and torque was observed on the (National Renewable Energy Laboratory) NREL Phase VI wind turbine. In addition, the maximum deflections of the blades were observed after the blades passed the tower with 20 to 40∘ at wind speeds of 7 and 20 m s−1, respectively. At 20 m s−1, the torque on the elastic blades showed a 13 % increment from the rigid ones, which was attributed to the rapid blade oscillation. Furthermore, Yu and Kwon (2014) performed a loosely coupled CFD-CSD simulation of the NREL 5 MW reference wind turbine. Results showed that due to the blade deformation, the blade aerodynamic loads are significantly reduced. In addition, the aerodynamic loads are abruptly dropped as the blades pass by the tower, resulting in oscillatory blade deformation and vibratory loads, particularly in the flapwise direction.
1.4 Objective
The aim of this work is to develop a high-fidelity model of wind turbine aerodynamics and structural dynamics to investigate blade–tower interaction. Coupled CFD-CSD simulation is performed to predict flow structure and to study the response of the wind turbine structure (namely the tower). The previous publication focused on the effect of tower shadow on the blades and assumed rigid tower. In this work an elastic tower in addition to elastic blades has been introduced. Using this method, the aerodynamic loads on the tower can be predicted with much more detail than using the classical BEM (blade element momentum) method and consequently structural dynamics.
Meeting such an objective could provide recommendations for wind turbine structure optimization and improve their design. As early outcome, the tower weight, size, and cost could be reduced. Furthermore, the detailed results of this study can be used to improve simplified engineering models to take into account blade–tower interaction effects.
The developed wind turbine simulation tool consists of three solvers: the CFD solver to predict the aerodynamic load, the FE solver to compute structure response, and the dynamic mesh solver to update the grid position. The coupling between the fluid solver and the structure solver is implemented based on the partitioned approach, where each solver works independently from the other.
Modeling a complete aeroelastic wind turbine poses a huge number of challenges. For instance, the aeroelastic model should satisfy the following requirements.
-
consider air damping in addition to structure damping;
-
support more than one elastic body interacting with each other (rotor blades and the support structure);
-
provide an appropriate presentation of the blade structure as the blades have numerous composite layers making the calculation very computationally expensive;
-
should be able to operate in a transient state so that the output can be used to compute the response of the structure in the time domain.
The choice of using the commercial software Ansys has been made by taking into account the advantage of stability and the availability of multiphysics tools in the software. In the following sections, the wind turbine specifications, flow, and structure solvers and the coupling approach will be presented.
2.1 Wind turbine specification
The simulation is performed for a 5 MW upwind horizontal axis wind turbine. The specifications of the wind turbine are given in Table 1. The wind turbine is equipped with three NREL 5 MW blades, each blade has varying DUxx and NACA64 airfoil series along the blade spans. The blade has a maximum chord length and twist angle of 4.65 m and 13.3∘, respectively (Jonkman, 2009). In order to simulate the flexible turbine and to simplify the grid generation process, some modification to the original turbine design has to take place. The hub geometry is approximated to a simple cylindrical shape, and its diameter is slightly increased; the blade roots were cut so that the blades are not physically attached to the hub anymore. Finally, nacelle geometry is not considered in the simulation model (although its weight is considered in the model). The reason behind these changes will be discussed in the next section; nevertheless, the aerodynamic or structural effects of these changes are expected to be rather small.
2.2 Flow solver
The Navier–Stokes (NS) equations are solved in three dimensions for an incompressible flow using the commercial software Fluent (ANSYS Inc., 2018). Fluent is a general fluid dynamics software integrated into ANSYS Workbench, which is an engineering simulation tool provided by ANSYS. The NS equations are discretized in the domain by means of the finite volume method, where the applied mathematical conservation equations (mass, momentum, and energy) are solved separately. The SIMPLE algorithm solves the pressure and the momentum equations in a predictor–corrector fashion. The convective flux is computed using the second-order upwind differencing scheme (SUDS) in which the viscous term is discretized with the second-order central difference scheme (ANSYS Inc., 2018). As the flow is strongly turbulent near the rotor, the k–ω SST (shear stress transport) turbulent model is adopted. It is considered one of the most accurate turbulent models in the RANS class to predict the turbulent viscosity.
2.3 Structure solver
The dynamic response of the flexible wind turbine model is computed in the “Transient Structural” solver of Ansys (ANSYS Inc., 2018). The software uses the finite element method to solve the set of partial differential equations of the equations of motion, which can be written after assembling the finite element matrices and vectors as
where M, C, and K are the mass, damping, and stiffness matrices, respectively; Fg, Fc, and FAero refer to the external load acting on the wind turbine structure due to gravitational, centrifugal, and aerodynamic forces, respectively; and x is the nodal displacement vector (Öchsner and Merkel, 3013). The aerodynamic force (FAero) is provided from an external module, where in this case the aerodynamic forces are calculated in the CFD solver.
2.4 Dynamic grid solver
To take into account the motion of the structure in the CFD domain, the computational grid has to move according to the motion of the structure in both the space and time domains. An appropriate dynamic mesh method is necessary to avoid re-mashing the high-computational-cost process and to ensure an efficient, robust, and smooth grid motion. The adopted dynamic mesh solver in this model is based on the diffusion method, where the motion of the grid is governed by a diffusion equation:
Here u is the mesh displacement velocity, and γ is the diffusion coefficient (ANSYS Inc., 2018). The boundary condition of the deforming surfaces is defined in such a way that the mesh motion is tangent to the boundary (that is, the normal velocity component vanishes). The Laplace equation describes the motion of the CFD computational grid, which is controlled by the diffusion coefficient. A constant diffusion coefficient refers to a uniform diffusion of the boundary motion through the grid.
In this model, the diffusion coefficient is set as a function of the boundary distance so that the high-diffusion regions in the vicinity of the moving boundaries tend to move together. As a result, the refined cell height, growth ratios, and quality near the structure surfaces are preserved.
2.5 Coupling approach
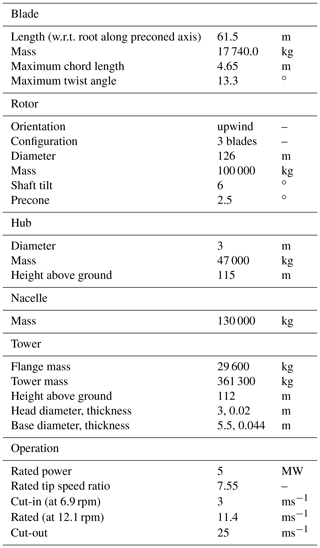
As the clearance between the blade and tower is of great interest, it is important that the flow solver sees the new position of the deformed blade. Therefore, the strong couple method is adopted in the simulation model. The procedure of the CFD-CSD analysis is presented in Fig. 1.
The simulation starts with a nondeformed structure, and the flow solver computes the velocity and pressure distribution in the computational domain. Once the quasi-steady solution converges, the aerodynamic load is transferred to the CSD solver to compute the structure deformation. The new position of the deformed structure is then provided back to the CFD solver by updating the grid using the dynamic grid solver.
In the next time step, the aerodynamic load in the CSD solver is calculated by taking into account the difference between the current load and previous coupled iterations as
The coupling between the two computational domains is done by assigning each element in the flow domain to the nearest structure node in the structure domain in a process known as mesh mapping. Hence, the predicted forces and moment on each cell face in the fluid domain is projected onto the finite element nodes in the structure domain.
2.6 CFD computational domain and grid generation process
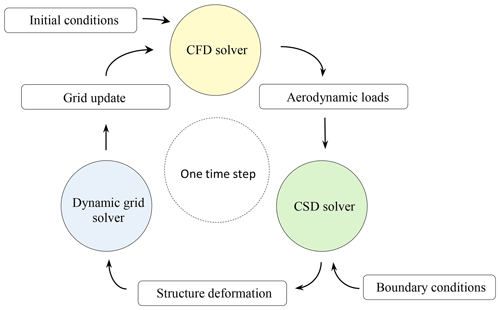
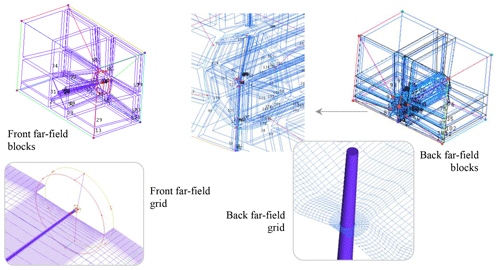
The computational domain has a rectangular shape where the turbine model is positioned in the middle. The inlet and outlet are placed 3 D (rotor diameter) upstream and 3.5 D downstream, respectively, and the sides are 2.5 D each from the turbine geometry (Fig. 2). To simplify the grid generation process, the wind turbine geometry and its domain are segmented into five separated sections, where each flexible component (i.e., the blades and the tower) has its own domains. This design is necessary to allow for the deformation and motion of the wind turbine structure and to avoid grid element collapse. Block structured grids with various types of grid topologies are adopted to generate a high-quality grid for each individual domain separately.
Wind turbine blades are considered to be a complex geometry due to the thin and curved shape and large dimensions ratio. The mesh strategy for such a complicated system has a significant impact on the quality and accuracy of the results. As the structure deforms, the grid in the CFD domain has to be conformal to avoid elements high distortion. ANSYS ICEM CFD is one of the most advanced and powerful grid generation tools currently available. The software uses a multiblock strategy to obtain a high level of control on cell shapes, distribution, and size and accurate fitting of the geometry. The structured grid in ICEM CFD consists of pure hexahedral elements. This kind of mesh is difficult to generate for complex geometries since the grid lines should not cross each other. On the other hand, it provides very good grid quality, which is essential for fluid–structure interaction (FSI) applications.
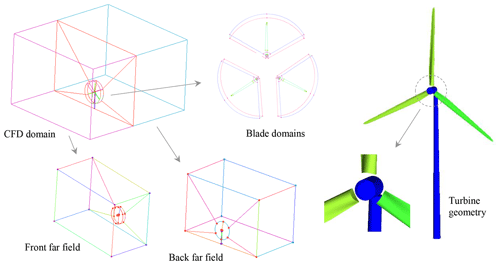
The blade domain is a one-third cylinder with an inclined surface to the back, allowing the blade tip more space to deform in the flapwise direction (Fig. 3). The grid generation process starts with creating an initial block then segmenting it into smaller blocks where their vertices, edges, and surfaces are associated with the blade geometry to adopt the shape of the blade. The blocking strategy that is used in the blade domain consists of a C grid and H grid. The C grid is used to capture the airfoil shape and create the refined high-quality boundary layers around the blade surfaces, while the H gird is set for the rest of the domain (Lecheler, 2009). To avoid grid-element-collapse problems resulting from blade deformation, the blade roots were detached from the hub surface by cutting 1.5 m of the roots. Hence, each blade is placed in its own domain without having contact with the domain surfaces.
The rectangular far-field domain is further segmented into two sections: front and back (Fig. 4). The front far field is the simplest part of the domain as it has no flexible bodies. The domains of the tree blades are placed at the inner end of the front far field; therefore, it has to feature a non-meshed space at the rotor position. The last domain is the back far field which includes the tower. The grid in this domain consists of an O grid surrounding the tower surface and H-grid for the rest of the domain (Lecheler, 2009). The coupling between the rotor and the tower is done by using the nonoverlapping sliding interface approach so that it is possible to rotate the blades while keeping the tower stationary.
Each blade was meshed with 51 elements around the airfoil section, and the tower has 40 elements around its section. The first layer is located at 10−2 m above the blade and tower surfaces with a growth ratio of 1.3. At the end of the grid generation process, a total of 295 structure blocks are created to generate about 3 million elements. Based on the computational domain grid generation strategy, the nacelle was removed to avoid grid collapse due to the small distance between the nacelle and the back far-field interface surfaces. The implemented structure blocking strategy comes out with a suitable compromise among mesh size, grid resolution, and cell quality.
2.7 Wind turbine structure model
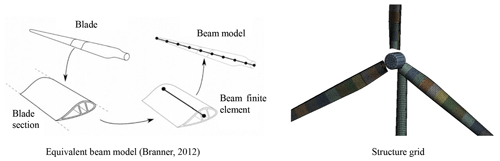
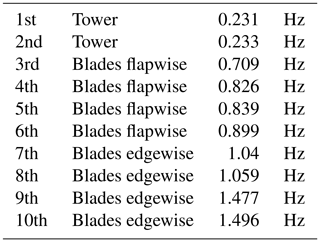
Modeling of the wind turbine tower in the structure solver is very simple as the tower geometry is considered to be a simple cylinder structure. On the other hand, the presentation of the blade's structure is quite challenging as the blades are made of numerous composite layers. To simplify blade structure presentation, the blades are modeled as a reduced equivalent beam using the classical beam element theory (Thomson, 1966; Quaranta et al., 2005). The simple multibody approach models the blade as a series of rigid sections hinged and linked together with springs and dampers to represent structure stiffness and damping, respectively. The beam model is computationally efficient as it reduces the number of degrees of freedom and provides an accurate blade deformation. Each blade surface is segmented into 20 sections along the blade span, and the flapwise, edgewise, and torsional stiffnesses and damping coefficient are defined (Fig. 5).
The wind turbine structure has been discretized with triangular and rectangular shell elements and each has three and four nodes, respectively. Each node has six degrees of freedom: three global translations and three global rotations. The final model has a total of 27.5 thousand elements that represent a sufficient element size to provide a grid independency solution.
2.8 Simulation setup
As Ansys does not support rotation of the structure when it is coupled to the CFD solver, the simulation of the flexible wind turbine model is done in two steps. First the simulation is performed for flexible blades keeping the tower rigid. In this case, the blades are rotating in the CFD domain while the structure solver computes the deformation of the individual stationary blades. Using this approach, it is not possible for the gravitational force to be considered in the structure model, and therefore it has not been included. However, the centrifugal force due to the rotor rotation has been taken into account as it represents a radial force independent from the blade position. The deformations of the blades are computed based on the aerodynamic load of the CFD solver. The forces and moments of the rotor are recorded from the CFD domain at the position of the tower head during the simulation time for the second simulation step.
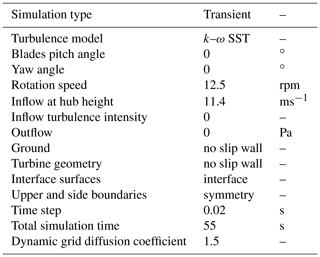
In the second simulation step, the simulation of the same case is repeated but this time the tower is considered to be flexible. The forces and moments that have been recorded from the first simulation step are set at the tower head. The rotor position in this simulation case is shifted with a mean tower deformation to the back so that the distance between the blades and the tower is approximately conserved. Running the simulation for the second step allows the tower to see the flexible blades rotating in front of it in the CFD domain and to feel blade vibrations as the loads are placed at the tower head from the first simulation. Using this approach, the rotor will not feel the vibrations of the tower as they are not connected physically. The transient FSI simulation is performed for the following operation conditions in Table 2.
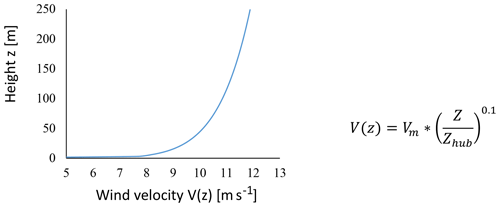
Wind speed gradient (wind shear) has been considered at the inflow with a velocity profile following the power law function in Fig. 6. In the function shown in Fig. 6, V(z) is the velocity at any height, Vm is the mean velocity (in this case 11.4 m s−1), Z is the height, and Zhub is the hub height. The flexible tower in the second simulation case is fixed to the ground at the bottom, and the hub is considered as a rigid rotating body in both simulation steps. Table 3 shows the natural frequencies of the system where for the mentioned operation the system does not run in the resonance region.
After performing the first simulation step (flexible blades and rigid tower), the forces and moments of the rotor are averaged for the last four cycles and set at the tower head. The static simulation of the tower showed a tower head mean deformation of about m or 0.79 % of tower length and m downstream and to the side, respectively. Based on the new position of the tower head, the second simulation step (flexible blades and tower) was run after shifting the rotor to the new mean tower displacement position.
3.1 Aerodynamic performance
3.1.1 Tower forces
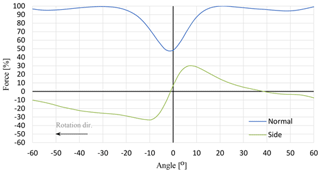
The motion of the blades in front of the tower will deflect the wind, causing a change in the stagnation point on the tower front surface. The tower suffers from a pressure drop three times per revolution, known as 3P oscillations for three-blade rotors. Figure 7 shows the aerodynamic forces on the tower for a one-third rotor revolution, where 0∘ represents the location of the tower. Each force component is plotted in percentage of its maximum value. The maximum normal force drop occurs after the blade passes the tower with a few degrees as the blade shadow reaches the tower. A maximum of 14.85 kN normal force is obtained on the tower over a one-third rotor revolution. As the blade reaches the tower, a drop of about 52 % of the normal force is observed. The numerical model has been validated with a wind tunnel test of a scaled model. The pressure on the front surface of the tower has been recorded over time by means of pressure sensors. Results have shown a correlation between measurements and the numerical model; more details about the test can be found in Shkara et al. (2017).
Furthermore, passage of the blades in front of the tower induces a side force fluctuation in a short time. A maximum of 5.37 kN is observed on the tower, which represents ±30 % of the maximum normal force. These forces are caused by a bound vortex circulation of the blades that disturbs flow streamlines on both tower sides.
3.1.2 Rotor thrust
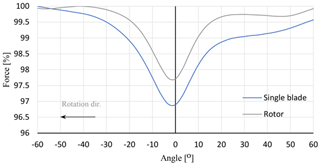
The effect of the blade–tower interaction is not only restricted to the tower, because the blade itself suffers aerodynamic impulsive forces as well. An individual blade thrust drop of about 3.1 % (6.2 kN) is noticed as the blade passes through the tower shadow. Figure 8 shows the thrust distribution of the blade that passes in front of the tower and the thrust of the complete rotor for one-third rotation. In general, for the mentioned simulation conditions, a total rotor thrust drop of about 2.3 % three times per revolution is observed.
3.1.3 Rotor torque
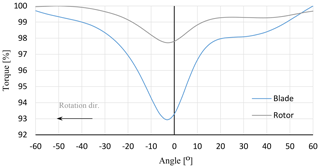
Figure 9 shows the generated torque of a blade passing in front of the tower and the total torque of the rotor for one-third of a rotor revolution. The influence of blade passage in the vicinity of the tower results in a sudden decrease in the blade lift force, which consequently causes a rapid decrease in blade torque. An individual blade torque drop of about 67.8 kN m (7 %) is observed as the flexible blade passes in front of the tower. Furthermore, a rotor torque drop of 66.5 kN m (2.3 %) occurs three times per revolution.
The results of this simulation are in good agreement with the simulation by Früh et al. (2008). Moreover, similar flexible blade torque behavior is reported by Gebhardt and Roccia (2014). The 2-D analysis of Früh et al. (2008) showed that movement of the blade in front of the tower will not only create effective velocity pulse but also results in a sharp change in the angle of attack of around 10 %. Becker (2017) showed in their CFD-CSD model of the NREL 5 MW that, due to the blade elasticity, the torque deviation increased with respect to the rigid blade assumption. The effect of torsional deformation has been investigated by Yu and Kwon (2014) for the same simulation conditions (except wind profile). In their model, 6 % rotor torque drop is noticed when the blades are considered to be flexible.
3.2 Structural dynamics
3.2.1 Dynamic response of the tower
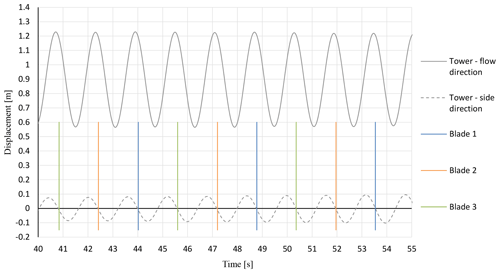
Figure 10 shows the displacement of the tower head in both downstream and side directions for the second simulation step. The vertical lines refer to the time point when the blades are positioned in front of the tower. The interaction between the rotor and the tower can be seen clearly in the displacement of the tower in both directions. A tower oscillation of m (±36.9 % of the mean deformation) and m (±10.8 % of the mean deformation) downstream and to the sides are observed, respectively. The tower is vibrating with a frequency of about 0.625 Hz, which represents a one-third rotation of the rotor in the time domain.
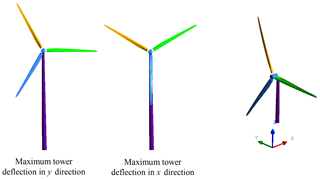
Although the complete wind turbine geometry is expected to experience less thrust due to the reduction of the tower projected area, the maximum tower deformation in the flow direction occurred when one of the blades is located in front of the tower. The reason behind that is related to the azimuthal position of the other two blades (Fig. 11). At this time, the two other blades are located at the upper half sector of the rotor disk (above the tower head), resulting in a higher bending moment than the vertical blade and leading to further tower downstream displacement. That means, for these operation conditions (probably for different operation conditions as well), the azimuthal position of the rotor blades will primarily influence tower deformation in comparison to the blade passing in front of the tower. Moreover, considering wind shear, rotation of the blade in the upper half sector will lead to increasing their thrust force, causing a higher bending moment than the lower half sector.
Similar to the tower deformation in the flow direction, tower head side displacement is synchronized with the azimuthal rotor angle as well. The side deformation of the tower in this case is resulting from the combination of the asymmetric rotor moment around the tower axis and the side component of the induced aerodynamic force caused by the blade rotation in front of the tower. The maximum deflection of the tower in the side direction is observed when two of the blades are positioned on one side and the third blade is on the opposite side (Fig. 11).
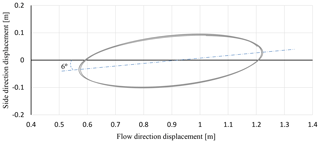
The motion of the tower head for the second simulation step is plotted on a 2-D plane in Fig. 12. The interface between the two displacements (flow and side directions) causes tower head motion following an elliptical pattern. The elliptic motion is inclined with an angle of 6∘ from the flow stream, which is determined by the side displacement amplitude. This angle will be changed if the wind speed or the blade's pitch angle changes.
3.2.2 Dynamic response of the blades
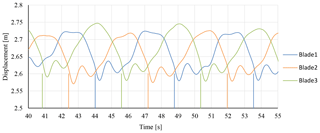
The flapwise displacements of the three blades over the time for the last 15 s are plotted in Fig. 13. A mean flapwise deflection of about 2.65 m is reached by the three blades, which corresponds to 4.3 % of the blade length. The three blades oscillate with a phase shift of 120∘ from each other showing that a coherent blade oscillation corresponds to the geometric layout of the blades in the rotor. The peak-to-peak deflection amplitude is about m, which corresponds to 6 % of the mean deflection. Two main signals can be observed: the large-amplitude one with a frequency of 0.208 Hz results from the wind shear that tends to excite the blade vibration more than blade–tower interaction. A similar blade response has been noticed in the work by Yu and Kwon (2014) as the blades passed by a rigid tower and the model of Tang et al. (2017) when the blade passes a flexible tower in their combined vortex wake and multibody dynamics model. The biggest flapwise deflection occurs at about 225∘ from the tower position, which is expected as the blade is subjected to the highest thrust when the blade is at the top (highest wind speed). The minimum blade displacement is observed at about 15∘ after the blades pass through the tower shadow.
The influence of the blade–tower interaction appears as a small dip in the displacement of the blade's tip with an amplitude of m (±1.9 % of the blade mean deflection) after the blade passes the tower. A response delay of about 0.5 s or 38∘ azimuthal angle is noticed. The structure delay responses of the blades and the tower are related to the structure inertia. Similar lag time structure responses have been observed by Tanget al. (2017) as well due to the aeroelastic effects.
A CFD simulation of the same rotor and boundary conditions, but with bigger tower diameter and predeformed blades based on BEM calculation, has been performed by Shkara et al. (2018). In comparison to the deformation of the BEM method, the mean flapwise deflection of the current flexible model showed a higher blade flapwise deflection by m (14 %). This indicates that CFD thrust force is slightly higher than the BEM method or vice versa. However, the difference is very small and has a rather neglectable influence on the wind turbine performance.
The obtained flapwise deflection is relatively small compared to what has been achieved in previous publications (Jeong et al., 2013; Becker, 2017; Dose et al., 2018) for the same simulation conditions. The reason behind this lies in the consideration of the centrifugal force in the current model. Rotation of the blades creates a centrifugal force that can reach up to 8g in magnitude, causing an increase in blade stiffness in both flapwise and edgewise directions and altering their natural frequencies (Bertagnolio et al., 2002). As a result, blade deformation is considerably decreased compared to a stationary blade subjected to the same load.
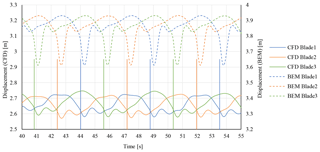
The simulation of the same wind turbine model has been performed using the blade element momentum (BEM) method and multibody dynamics approach for a rigid tower. Figure 14 shows a blade's flapwise displacements of the CFD and the BEM models. It is clear that the BEM method predicted higher mean blade deformation than CFD. A mean blade flapwise displacements of 3.9 m is obtained using the BEM method compared to 2.65 m using CFD, which corresponds to a difference of 32 %. The response of the blades as they pass in front of the tower shows very similar behavior for both methods (i.e., CFD and BEM). However, the oscillation amplitudes of the BEM blades are bigger than the CFD. The peak-to-peak deflection amplitude is about m in the BEM model compared to only m in CFD, which corresponds to 50 % lower blade deflection oscillation amplitude.
The reason behind the differences in the displacements is related to the fact that the aerodynamic damping is not considered in the BEM model, which is part of the solution of the CFD. In addition, the BEM method predicted higher rotor thrust than the CFD by about 22.4 %. The higher blade displacements resulting from the BEM method can be related to the fact that the BEM does not predict the thrust accurately in the case of flow separation or overestimate it, which in this case occurs near the blade's root. Furthermore, BEM can give only one constant value for a certain operation condition (as the method is based on the wind tunnel measured lift and drag coefficients). In contrast, CFD uses advanced turbulent models to predict the transient lift and drag forces of the blades, which might be different from the previous rotation of the same blade position.
The blade structure behaves like a spring: the more you compress it, the higher the displacement amplitude will be. Therefore the displacement amplitude of the BEM blade is greater than the CFD model as it passes through the tower shadow.
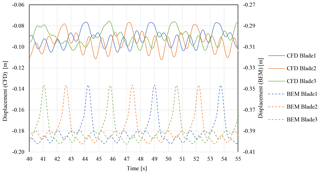
A mean deflection of about 10−1 m is observed in the edgewise direction with an oscillation amplitude of about m or ±0.6 % of the mean blade deformation (Fig. 15). The amplitudes of the edgewise displacements are very small, which is due to the fact that gravity is not considered for the blade's structure. Similar to the flapwise oscillation, the blades vibrate in the edgewise direction because aerodynamic forces change over the azimuth angle (wind shear) and the interaction with the tower shadow. Furthermore, the blades vibrate because of the turbulent nature of the flow over the blade profile, although the incoming flow is uniform. Früh et al. (2008) showed in their study that the flow over a wind turbine is either fully turbulent as a consequence of the turbulent intensity in the atmospheric flow or the transition occurs mostly at a distance of 10 % of the blade leading edge.
Similar to the blade's flapwise deflections, the blade's edgewise deflections of the BEM model are higher than the CFD model. The BEM model showed a mean blade edgewise deflection of m with an oscillation amplitude of about m due to the passage of the blades in the tower shadow. The blade's edgewise deflection is related to the blade's torque, which in the case of the BEM model is higher than the CFD model by 19 %.
In this paper, a coupled CFD-CSD numerical simulation method is presented to investigate the dynamic response of a 5 MW upwind wind turbine structure taking into account blade–tower interaction. The coupling between the fluid solver and the structure solver was implemented based on a partitioned approach. Both the blades and the tower are considered to be flexible for the nominal operation condition simulation. The results showed a tower mean displacement of about 0.79 % of tower length downstream with an oscillation amplitude of ±36.9 % and ±10.8 % of the mean deflection downstream and to the sides, respectively. The interaction with the tower causes blade's oscillation in both flapwise and edgewise directions with a phase shift of 120∘ from each other. The highest deformations of the blades were dominated by the wind shear, and the rotor azimuthal angle described the motion of the tower head. The influence of the blade–tower interaction appears as a small dip in the displacement of the blade's tip with an amplitude of 1.9 % of the blade mean deflection and a sudden rotor torque drop of 2.3 % three times per rotation. The simulation of the same wind turbine model has been performed using a blade element momentum (BEM) method with multibody dynamics approach for a rigid tower. The simulation results showed that the BEM model overestimates both rotor thrust and torque, which resulted in higher blade flapwise and edgewise deflections and their oscillation amplitudes. The additional cyclic aerodynamic loads on both the tower and the blades due to the blade–tower interaction induces fatigue loads which are considered essential for the structure lifetime prediction and analysis.
The data presented in the figures are available at https://doi.org/10.23728/b2share.498ae39b13c04e0f9dfdbfb711ac21f5 (Shkara, 2020).
YS performed the fluid–structure interaction simulation, did all the analysis of results, and wrote the article. MC conducted the dynamic simulation of the wind turbine based on the blade element momentum (BEM) method and multibody dynamics approach and provided the data for Figs. 14 and 15. RS and GJ supervised the research. All authors reviewed the final article.
The authors declare that they have no conflict of interest.
This paper was edited by Mingming Zhang and reviewed by Abdul Baseer and one anonymous referee.
Ahlstrom, A.: Influence of wind turbine flexibility on loads and power production, Wind Energy, 9, 237–249, https://doi.org/10.1002/we.167, 2006.
ANSYS Inc.: available at: http://www.ansys.com (last access: 5 September 2019), Release 19.1, 2018.
Becker, M.: fastFoam an aero-servo-elastic wind turbine simulation method based on CFD, MS thesis, Delft University of Technology, 2017.
Bertagnolio, F., Gaunaa, M., Hansen, M., Sorensen, N., and Rasmussen, F.: Computation of aerodynamic damping for wind turbine applications, 4th GRACM Congress on Computational Mechanics, 2002.
Branner, K., Blasques, J. P., Kim, T., Fedorov, V. A., Berring, P., Bitsche, R. D., and Berggreen, C.: Anisotropic beam model for analysis and design of passive controlled wind turbine blades, DTU Wind Energy report E-0001 (EN), DTU Wind Energy, ISBN 978-87-92896-01-8, 2012.
Carrion, M., Steijl, R., Barakos, G. N., Gomez-Iradiy, S., and Munduatey, X.: Coupled CFD/CSD method for wind turbines, 11th World Congress on Computational Mechanics – WCCM XI 2014, Barcelona, Spain, 2014.
Chattot, J. J.: Extension of a helicoidal vortex model to account for blade flexibility and tower interference, J. Sol. Energ.-T. ASME., 128, 455–460, 2006.
Council Directive 96/53/EC: Laying down for certain road vehicles circulating within the Community the maximum authorized dimensions in national and international traffic and the maximum authorized weights in international traffic, Official Journal of the European Communities, 1996.
Danish Standard DS 472: Load and safety for wind turbine construction, 2009.
Dose, B., Rahimi, H., Herráez, I., Stoevesandt, B., and Peinke, J.: Fluid-structure coupled computations of the NREL 5MW wind turbine by means of CFD, Renew. Energ., 129, 591–605, https://doi.org/10.1016/j.renene.2018.05.064, 2018.
EWEA Wind Directions: The Economics of Wind Energy, available at: https://www.ewea.org/ (last access: 23 April 2019), Belgium, Brussels, 2007.
Früh, W. G., Seume, J., and Gomez, A.: Modelling the aerodynamic response of a wind turbine blade passing in front of the tower, European Wind Energy Conference, 6, Brussels, Belgium, ISBN 978-1-61567-115-1, 2008.
Gebhardt, C. G. and Roccia, B. A.: Non-linear aeroelasticity: An approach to compute the response of three-blade large-scale horizontal-axis wind turbines, Renew. Energ., 66, 495–514, https://doi.org/10.1016/j.renene.2013.12.040, 2014.
Gomez, A. and Seume, J.: Aerodynamic coupling of rotor and tower in HAWTs, Proceedings of the European Wind Energy Conference, 6, Marseille, France, ISBN 978-1-61567-746-7, 2009.
Hansen, M. O. L., Sorensen, J. N., Voutsinas, S., Sorensen, N., and Madsen, H. A.: State of the art in wind turbine aerodynamics and aeroelasticity, Prog. Aerosp. Sci., 42, 285–330, https://doi.org/10.1016/j.paerosci.2006.10.002, 2006.
Hsu, M. C. and Bazilevs, Y.: Fluid–structure interaction modeling of wind turbines: Simulating the full machine, Comput. Mech., 50, 821–833, https://doi.org/10.1007/s00466-012-0772-0, 2012.
IEC 61400-1: Wind turbines – Part 1: Design requirements, International Electrotechnical Commission, available at: https://www.iec.ch/ (last access: 17 February 2018), Third edition, Geneva, Switzerland, 2005.
Janajreh, I., Talab, I., and Macpherson, J.: Numerical simulation of tower rotor interaction for downwind wind turbine, Journal of Modelling and Simulation in Engineering, 2010, 860814, https://doi.org/10.1155/2010/860814, 2010.
Jeong, M. S., Kim, S. W., Lee, I., Yoo, S. J., and Park, K. C.: The impact of yaw error on aeroelastic characteristics of a horizontal axis wind turbine blade, Renew. Energ., 60, 256–268, https://doi.org/10.1016/j.renene.2013.05.014, 2013.
Jonkman, J., Butterfield, S., Musial, W., and Scott, G.: Definition of a 5-MW Reference Wind Turbine for Offshore System Development, NREL/TP-500-38060, Golden, CO: National Renewable Energy Laboratory, 2009.
Kim, H., Lee, S., and Lee, S.: Influence of blade-tower interaction in upwind-type horizontal axis wind turbines on aerodynamics, J. Mech. Sci. Technol., 25, 351–1360, https://doi.org/10.1007/s12206-011-0311-5, 2011.
Lackner, M. A., Develder, N., and Sebastian, T.: On 2D and 3D potential flow models of upwind wind turbine tower interference, Comput. Fluids, 71, 375–379, 2013.
Lecheler, S.: Numerische Strömungsberechnung – Schneller Einstieg durch ausführliche praxisrelevante Beispiele, ISBN 978-3-8348-0439-6, 2009.
Milne-Thomson, L. M.: Theoretical aerodynamics, New York, Dover Publications, 1966.
Öchsner, A. and Merkel, M.: One-Dimensional Finite Elements an Introduction to the FE Method, ISBN 978-3-642-31796-5, https://doi.org/10.1007/978-3-642-31797-2, 2013.
Quaranta, G., Masarati, P., and Mantegazza, P.: A Conservative Mesh- Free Approach for Fluid–Structure Interface Problems, International Conference on Computational Methods for Coupled Problems in Science and Engineering, 1–23, 2005.
Rauh, A. and Peinke, J.: A phenomenological model for the dynamic response of wind turbines to turbulent wind, J. Wind Eng. Ind. Aerod., 92, 159–183, 2004.
Shkara, Y.: Aeroelastic response of a multi-megawatt upwind horizontal axis wind turbine (HAWT) based on fluid–structure interaction simulation, https://doi.org/10.23728/b2share.498ae39b13c04e0f9dfdbfb711, 2020.
Shkara, Y., Werkmeister, A., Fontecha, R., Jacobs, G., and Schelenz, R.: An experimental and computational investigation of wind turbine blade-tower aerodynamic interaction, 13th biennial German Wind Energy Conference DEWEK, 2017.
Shkara, Y., Schelenz, R., and Jacobs, G.: The effect of blade-tower interaction on the structure loading of multi megawatt horizontal axis wind turbine, J. Phys. Conf. Ser., 1037, https://doi.org/10.1088/1742-6596/1037/7/072033, 2018.
Tang, D., Bao, S., Luo, L., Mao, J., Lv, B., and Guo, H.: Study on the aeroelastic responses of a wind turbine using a coupled multibody-FVW method, J. Energy, 141, 2300–2313, https://doi.org/10.1016/j.energy.2017.11.105, 2017.
Tavner, P. J., Xiang, J., and Spinato, F.: Reliability analysis for wind turbines, Wind Energy, 10, 1–18, 2007.
Wang, Q., Zhou, H., and Wan, D.: Numerical Simulation of Wind Turbine Blade-Tower Interaction, Journal of Marine Science and Application, 11, 321–327, https://doi.org/10.1007/s11804-012-1139-9, 2012.
Yu, D. O. and Kwon, O. J.: Predicting wind turbine blade loads and aeroelastic response using a coupled CFD-CSD method, Renewable Energy, 70, 184–196, 2014.
Zhao, Q., Sheng, C., and Afjeh, A.: Computational aerodynamic analysis of offshore upwind and downwind turbines, Journal of Aerodynamics, 2014, 860637, https://doi.org/10.1155/2014/860637, 2014.